1.-Introducción. 2.- Unidades de medida de ángulos.

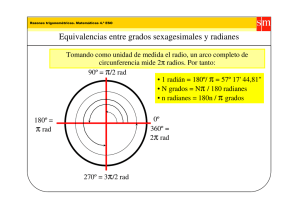
1º BCN-BT
Trigonometría
1.-Introducción.
La palabra trigonometría proviene del griego trigonos (triángulo) y metría (medida).
Etimológicamente, significa medida de triángulos. Es una parte de las Matemáticas que estudia las
relaciones métricas de los elementos de un triángulo (lados y ángulos). Su importancia como
auxiliar de otras ciencias es grande.
La trigonometría se emplea en Física para el estudio de los fenómenos vibratorios y
ondulatorios, en agrimensura, en navegación, en astronomía, etc. Si bien en astronomía más que la
trigonometría plana se emplea la trigonometría esférica.
2.- Unidades de medida de ángulos.
A.- Unidades principales.
El ángulo recto, el ángulo llano que es doble que un ángulo recto y el ángulo completo
que es el doble que un ángulo llano.
B.- Unidades secundarias.
Se estudian en función de tres sistemas de medidas:
a) Sistema sexagesimal. La unidad es el grado sexagesimal que es una de las 90 partes
iguales en las que se divide un ángulo recto. Un grado sexagesimal se representa: 1º. El grado
sexagesimal a su vez puede seguirse dividiendo en 60 partes, en 60 minutos, un minuto se
representa: 1´. El minuto a su vez en 60 partes dando lugar a 60 segundos, y un segundo se
representa: 1´´. Es fácil concluir que 1º = 3600´´
3.600''.
b) Sistema centesimal., La unidad es el grado centesimal
que es una de las 100 partes iguales en las que se divide un ángulo
recto. Un grado centesimal se representa: 1g. El grado centesimal
a su vez puede seguirse dividiendo en 100 partes, en 100 minutos,
un minuto se representa: 1m. El minuto a su vez en 100 partes
dando lugar a 100 segundos, y un segundo se representa: 1s. Es
fácil concluir que 1g = 3600s.
c) Radián. Es el ángulo central cuyo arco mide lo mismo
que el radio de la circunferencia con que ha sido trazado. Como la
circunferencia completa tiene 360º, y la longuitud de una circunferencia es de 2Π, podemos
concluir con las siguientes relaciones entre lo tres sistemas de unidades:
1 ángulo recto = 90º = 100g =
π
rad .
2
1 ángulo llano = 180º = 200g = π rad.
1 ángulo completo = 360º = 400g = 2π rad
En los problemas de trigonometría, astronomía, navegación resolución de triángulos, etc.,
comúnmente se usan las medidas de los ángulos en grados sexagesimales. La ventaja de los
radianes se verá en la representación y el estudio de las funciones trigonométricas:
Ejemplo.- Expresar en radianes, 99º.
Realizaremos una regla de tres: si 180º se corresponde con Π radianes, los 99º se corresponderán con x radianes:
180º → π rad 
99 π
9
=
π rad , observa que el resultado se expresa en forma de fracción, normalmente.
 x=
99º → x rad 
180 20
Ejemplo.- Expresa en grados sexagesimales 5Π/7 rad.
Página 1 de 2
180º → π rad 
5π ·180

7
= 128,57 º en este caso no ha dado un número natural, por lo tanto
5π
 x=
π
xº →
rad 
7

será necesario ver cuantos minutos y/o segundos le corresponden a esos 0,57 que le “sobran” al número natural 128. No pienses que
son 57´, no, por favor. Hemos tomado al dividir dos cifras decimales, luego 100 centésimas (una de cada cien), en cambio, 1º
sexagesimal son 60´(una de cada sesenta), luego... Por tanto es necesario convertir esos 0,57 grados sexagesimales:
Realizamos la misma regla de tres
1º → 60´ 
0,57 · 60
= 34,2´ tenemos un número natural de minutos, 34, y tenemos un resto de 0,2 minutos, que no son 2
x=
0,57 º → x 
1
segundos, ni 20 segundos, ¿verdad que no?, será necesario convertirlos:
1´ → 60´´
 x = 0,2 · 60 = 12´´ en definitiva, tenemos que: 5Π/7 rad=128º 34´ 12´´
0,2´ → x 
Ejemplo.- Expresa en radianes: a) 27°. b) 25° 30'. c) 40° 20' 15''.
a ) 27 º = 27
c)
π
π
= 3
rad
180
20
b) 25º 30´= 25,5º = 25,5
π
= 0,4451 rad
180
40° 20' 15'' , convertimos 15´´ en minutos (15/60=0,25´) que sumados a los 20 (20,25´)los convertimos a grados
20,25/60=0,3375º) que sumados a los 40º nos da: 40'3375° = 40'3375
π
180
= 0'704 rad. En éste caso hemos utilizado Π como
3,14 y hemos aproximado a la cuarta cifra decimal.
Ejemplo.- Expresa en el sistema sexagesimal: a)
π
rad =
9
Ejemplo.Ejemplo.a)
π
rad
9
2
rad
5
2
2 180º
b) rad = ·
= 22,929º = 22º55´44´´
5
5 π
b)
π 180º
= 20º
9 π
1 radián es igual a 57º17´45´´,71
1º son 0,0174... rad
Calculadora. Observa en la calculadora la tecla º ´ ´´, fuera de la tecla se observa una flecha. Anota en la calculadora
el número que te ha dado en la última división: 22,929, pulsa el botón SHIFT (en algunas calculadoras INV) y
posteriormente el botón º ´ ´´, observa el resultado. Dale ahora solo al botón º ´ ´´, ¿qué te parece?. Es necesario que la
calculadora tenga el MODE 4, que es DEG, en este modo de trabajo, la calculadora entiende que la información
suministrada es en el sistema sexagesimal. El MODE 5 es para trabajar en radianes, ya lo veremos más adelante.
Por otra parte, introduce en la calculadora el número 22, pulsa º ´ ´´, posteriormente 55 y pulsa º ´ ´´, y pro
último, 44 y pulsa º ´ ´´, en la calculadora aparece la expresión decimal, pulsa SHIFT ( o INV) º ´ ´´, aparece la
sexagesimal.
Ejercicios.
1.- Haciendo una tabla, expresa en radianes los siguientes ángulos:
0°, 15°, 22° 30', 30°, 45°, 60°, 75°, 90°, 120°, 135°, 150°, 180°, 210°,225°, 240°, 270°, 300°,
315°, 330°, 360°.
2. Un ángulo mide 3 radianes. Si dibujamos su arco tomando un radio de 5 cm., ¿cuánto medirá
dicho arco?
3. En una circunferencia de 10 cm. de radio, un arco mide 6 cm. ¿Cuánto mide (en grados y en
radianes) el ángulo correspondiente?
4. El radio de una circunferencia mide 6 cm. ¿Cuál es la longitud del arco correspondiente a un
ángulo de 20°?
π
5. Dos ángulos de un triángulo miden 50° y radianes . ¿Cuánto mide el otro ángulo? Da el
6
resultado en grados y en radianes.
Página 2 de 2