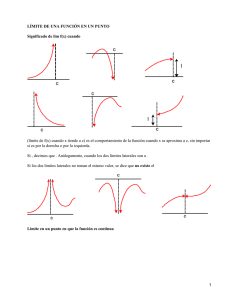
Límites infinitos y límites al infinito El símbolo se lee infinito, es de

Límites infinitos y límites al infinito
El símbolo se lee infinito, es de carácter posicional, no representa ningún número
real.
Si una variable independiente está creciendo indefinidamente a través de valores
positivos, se escribe
(que se lee:
de valores negativos, se denota como
Similarmente, cuando
tiende a más infinito), y si decrece a través
(que se lee:
tiende a menos infinito).
crece indefinidamente y toma valores positivos cada vez
mayores, se escribe
, y si decrece tomando valores negativos escribimos
.
Consideramos la función
definida por
para
determinar el comportamiento de la función cuando
. Vamos a
cuando
y cuando
. Para ello nos ayudamos de las tablas siguientes:
a.
En este caso, cuando
, la función
tiende a tomar
valores positivos cada vez mayores. Esto podemos escribirlo como
, es decir
b.
Ahora, cuando
toma valores cercanos a 2 pero menores que 2, la función
tiende a valores negativos cada vez menores. Es decir,
, o sea
.
cuando
c.
Ahora observe que es
la que tiende a tomar valores positivos cada vez
mayores, obteniendo como resultado que
Así
, o sea,
tiende a valores cercanos a cero.
cuando
.
d.
En forma similar a la tabla anterior se tiene que
cuando
es
decir,
Podemos representar gráficamente el comportamiento de la función
forma siguiente.
Consideramos ahora la función definida por
representación gráfica es la siguiente:
para
en la
, cuya
Podemos decir que:
a.
y
b.
y
Ejercicio
Determine:
,
,
utilizando para ello la función
,
,
,
,
.
Daremos ahora algunas definiciones sobre límites infinitos, y límites al infinito.
Definición
Se dice que
crece sin límite cuando
, si para todo número real
existe
tal que
Gráficamente se tiene:
siempre que
tiende a
, que se denota
, (sin importar su magnitud),
.
Esta definición nos dice que es posible hacer
tan grande como se quiera, (es decir,
mayor que cualquier número positivo ), tomando suficientemente cerca de .
Ejemplo
Consideremos la representación gráfica de la función
definida por:
Demostremos ahora que
Para hacer la prueba, debe establecerse que dado un
existe
.
Observe que:
.
tal que
Luego, dado
, escogemos
de tal forma que se satisfaga que
.
Si tomamos, por ejemplo,
cuando
cuando
, es decir,
.
Definición
Se dice que
decrece sin límite cuando
, si para todo número real
tiende a
, que se denota por
, existe una
tal que
Gráficamente se tiene que:
La definición anterior afirma que es posible hacer
menor que cualquier número
negativo , tomando suficientemente cerca de .
Ejemplo
Consideremos la representación gráfica de la función
definida por
Demostremos ahora que
Para hacer la prueba debe establecerse que dado un
, existe
siempre que
Observe que
(el sentido de la desigualdad cambia pues
).
Además
Note que
.
sí tiene sentido pues
Luego,
si y solo si
Así, dada
, existe
por lo tanto tomamos
,
tal que
Si por ejemplo, tomamos
que
entonces
.
siempre que
o sea
, por lo
siempre que
Definición
Se dice que
escribe
tiende a
cuando
tiende a por la derecha, y se
, si se cumple que a cada número positivo
, (tan
grande como se quiera), corresponde otro número positivo
de
) tal que
.
Similarmente, se dice que
escribe
tiende a
si
mayor que cero pues
, (que depende
cuando
tiende a
siempre que
ya que
por la izquierda y se
(Observe que
es
).
-El comportamiento de la función
por la definición anterior.
definida por
cuando
, está regido
Recuerde la representación gráfica de esta función hecha anteriormente.
-Los símbolos
en vez de
y
se definen análogamente, escribiendo
. (note que si
entonces
)
Gráficamente se tiene:
En esta representación gráfica se tiene que tanto al acercarnos a por la derecha como
por la izquierda, los valores de la función son negativos cada vez mayores, (mayores en
el valor absoluto), es decir, se tiene que
y cuando
Definición
Se dice que
cuando
es decir,
cada número positivo
existe otro número positivo
.
si para
, tal que
Podríamos representar gráficamente este comportamiento de una función
Observe que
como sigue:
y que
Podemos anotar que
Ejemplo:
Demostraremos que
Para probar este límite, se debe establecer que dado un
, debe existir
siempre que
Ahora, como
podemos tomar
Por ejemplo, si
a 1000 siempre que
si y solo si
, entonces, para cualquier número
de tal forma que se cumpla que
entonces
sea mayor que 10.
La función f definida por
siguiente
, con
. Esto significa que
,
.
es mayor
, tiene como representación gráfica la
Nota: En forma similar a la definición anterior pueden definirse
,
y
En las siguientes representaciones gráficas vamos a ejemplificar el comportamiento de
una función f en el que se evidencien los límites anteriores:
a.
b.
c.
Ejercicio:
En cada caso, utilizando el dibujo que se da, determine los límites que se indican:
a)
b)
a)
b)
c)
c)
d)
d)
Consideraremos ahora la función f definida por
En las siguientes tablas vamos a evidenciar su comportamiento cuando
cuando
a.
:
y
b.
En ambas tablas puede observarse que cuando
toma valores positivos o valores
negativos cada vez mayores, (mayores en valor absoluto), se tiene que la función
tiende a acercarse a 2, por lo que se puede escribir que:
y
A continuación hacemos la respectiva representación gráfica de la función
:
Damos ahora las definiciones para los límites cuyo resultado es una constante cuando
y cuando
Definición
Sea
una función con dominio
elementos de
El límite de
en el intervalo
cuando
existe un número
y
existen
.
tiende a más infinito es
, si para cada
para toda
tal que para cualquier número
.
, que se representa
tal que
Ejemplo
Probar que
Hay que demostrar que para
existe
tal que
si
Se tiene que
Si
entonces
Luego, dada
por lo que:
se cumple que
, por lo que podemos tomar
siempre que
Por ejemplo, si
si y solo si
de tal forma que se verifique que
.
entonces
, o sea, si
por lo que:
La representación gráfica de la función es la siguiente:
Definición
Sea
una función con dominio
elementos de
El límite de
en el intervalo
cuando
, existen
.
tiende a menos infinito es
, si para todo
para cada
tal que para cualquier número
existe un número
y
, que se representa
tal que
.
Ejercicio
Utilizando la definición anterior y un proceso similar al desarrollado en el ejemplo
inmediato anterior, pruebe que: