Sólidos
Anuncio
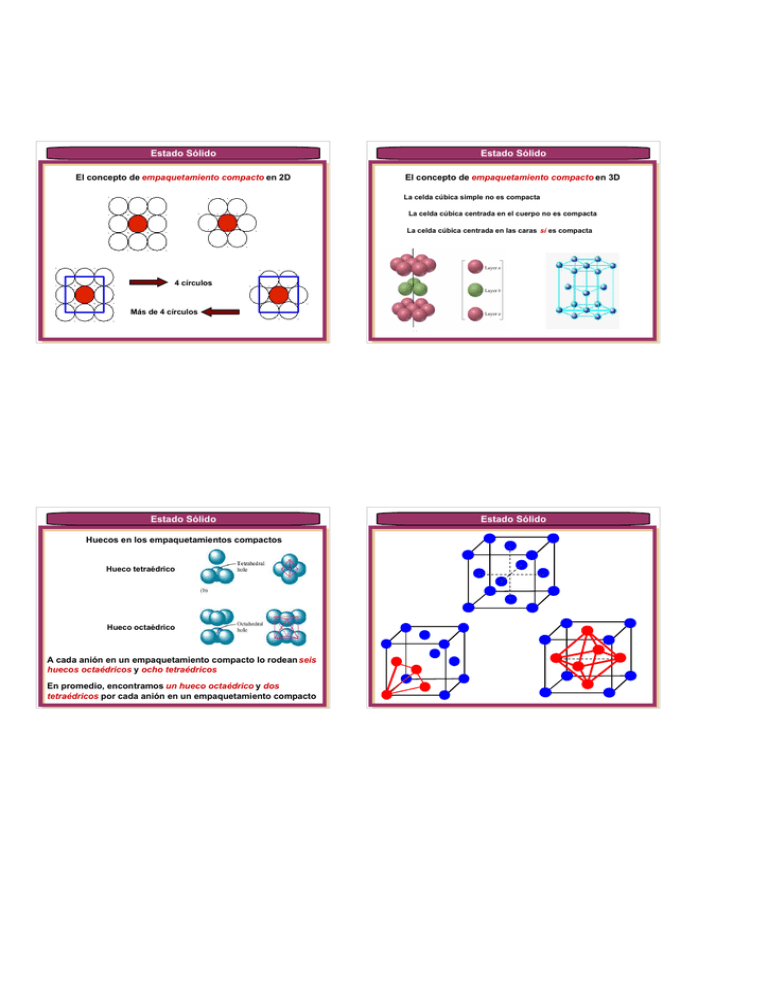
Estado Sólido Estado Sólido El concepto de empaquetamiento compacto en 2D El concepto de empaquetamiento compacto en 3D La celda cúbica simple no es compacta La celda cúbica centrada en el cuerpo no es compacta La celda cúbica centrada en las caras sí es compacta 4 círculos Más de 4 círculos Estado Sólido Huecos en los empaquetamientos compactos Hueco tetraédrico Hueco octaédrico A cada anión en un empaquetamiento compacto lo rodean seis huecos octaédricos y ocho tetraédricos En promedio, encontramos un hueco octaédrico y dos tetraédricos por cada anión en un empaquetamiento compacto Estado Sólido Estado Sólido Estado Sólido En sólidos iónicos, los aniones forman el empaquetamiento y los cationes ocupan los huecos El número de coordinación del anión, Na, en un sólido CcAa se calcula según Número de coordinación : en sólidos iónicos es el número de aniones que rodean a un catión o el número de cationes que rodean a un anión Nc x c = Na x a El número de coordinación del catión , Nc, depende de r c/ra El catión rodeado de Nc aniones de carga Qa siente una carga negativa total de Qa x Nc rc/ra Nc 0,22 – 0,41 4 Mayor carácter covalente 0,41 – 0,73 6 Mayor carácter iónico > 0,73 8 No es empaquetamiento compacto El anión rodeado de Na cationes de carga Qc siente una carga positiva total de Qc x Na La electroneutralidad se preserva sólo si Qa x Nc = Qc x Na Estado Sólido Estado Sólido Por otro lado, la fórmula CcAa nos dice que Qa x a = Qc x c Problema 5. ¿Cuántos aniones rodean a un anión determinado en un empaquetamiento compacto? Determinar Nc y Na para los siguientes sólidos iónicos: FeO, ZnS, CdCl2, CsCl. Dividiendo esta ecuación por Qa x Nc = Qc x Na En la misma capa: 6 En la capa superior: 3 a / Nc = c / Na En la capa inferior: 3 Na x a = Nc x c Total: 12 Comprobar con NaCl, MgO, CaCl 2, Al 2O3 Estado Sólido Estado Sólido Algunos sólidos iónicos típicos a. FeO rc: 82 pm ra: 132 pm rc / ra: 82 / 132: 0,62 Nc = 6 Na = N c rc: 74 pm ra: 184 pm rc / ra : 74 / 184: 0,40 Nc = 4 Na = N c rc : 103 pm ra : 181 pm rc / ra: 103 / 181: 0,57 Nc = 6 Na = Nc / 2 = 3 rc : 174 pm ra : 181 pm rc / ra: 174 / 181: 0,96 Nc = 8 Na = N c NaCl b. ZnS c. CdCl 2 d. CsCl Haluros alcalinos, óxidos alcalino-térreos y óxidos de metales de transición bivalentes Estado Sólido Estado Sólido CsCl CaF2 Ca2 + F- Cloruros, bromuros y yoduros de rubidio y cesio Fluoruros de metales bivalentes grandes Estado Sólido Estado Sólido Energía reticular de un sólido iónico ZnS Energía que se libera cuando se forma un mol del sólido a partir de sus iones en fase gaseosa Na+g + Cl-g NaCls Ur∝ Ur < 0 QaQc r ar c Q = cargas de los iones, r = radios iónicos Sulfuros de metales bivalentes y óxido de berilio Estado Sólido Ur∝ Estado Sólido QaQc r ar c Ur∝ Ur en kJ / mol Ur en kJ / mol Li+ Na+ F1036 923 Cl853 787 Br807 747 I757 704 K 821 715 682 649 785 740 689 659 660 631 630 604 + Rb Cs+ + QaQc r ar c OH- O2 - Na+ Mg2 + 900 3006 2481 3791 Al3 + 5627 15916 Estado Sólido Estado Sólido Problema 6. Cuál de los siguientes compuestos iónicos tendrá la mayor energía reticular? 1. MgCl2 Problema 7. Cuál de los siguientes compuestos iónicos requerirá más energía por mol que el CaS(s) para descomponerse en sus iones gaseosos? 1. NaF (s) 2. MgBr2 2. SrS(s) 3. NaBr 3. AlN(s) 4. CaCl 2 4. MgBr 2(s) 5. CaBr 2 5. SrSe(s) Estado Sólido Estado Sólido Ciclo de Born-Haber – una alternativa termodinámica al cálculo de la Ur El enlace metálico en la Tabla Periódica Na+( g ) + Cl-( g ) PI Ur NaCl( s ) Hf AE Hs u b l Na( g ) + Cl( g ) Na( s ) + Cl2 ( g ) ½Hd i s o c 1 H f U r H subl Hdisoc PI EA 2 Estado Sólido Números de coordinación en sólidos metálicos En un metal con estructura cúbica simple, el número de coordinación de cada átomo metálico es 6 Estado Sólido En un metal con estructura cúbica centrada en las caras, el número de coordinación de cada átomo metálico es 12 Estado Sólido En un metal con estructura cúbica centrada en el cuerpo, el número de coordinación de cada átomo metálico es 8