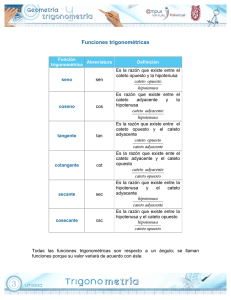
Teorema de la altura sobre la hipotenusa

TEOREMA DE LA ALTURA SOBRE LA HIPOTENUSA
Ejemplos
1. Si en un triángulo rectángulo sus catetos miden
respectivamente, calcular las longitudes de:
a)
b)
c)
d)
8 m y 15 m
La hipotenusa.
La proyección del cateto menor sobre la hipotenusa.
La proyección del cateto mayor sobre la hipotenusa.
La altura sobre la hipotenusa.
Solución
A
Sea c la longitud de la hipotenusa, para calcularla se aplica el teorema
de Pitágoras:
82  152  c2
 289  c2
 17  c
La hipotenusa mide 17 m .
B
Sea x la longitud de la proyección del cateto menor sobre la
hipotenusa, para calcularla se aplica el teorema del cateto:
82  x  17
 64  x  17

64
x
17
La proyección del cateto menor sobre la hipotenusa mide
C
64
m.
17
Sea y la longitud de la proyección del cateto mayor sobre la
hipotenusa, para calcularla se aplica el teorema del cateto:
152  y  17
 225  y  17

225
y
17
La proyección del cateto mayor sobre la hipotenusa mide
D
225
m.
17
Sea h la longitud de la altura sobre la hipotenusa, para calcularla se
aplica el teorema de la altura sobre la hipotenusa:
64 225

17 17
14400
 h2 
289
120
h
17
h2 
La altura sobre la hipotenusa mide
120
m.
17
2. Los lados de un triángulo rectángulo miden 48 cm, 55 cm, 73 cm
respectivamente. Calcule la longitud de la altura sobre la hipotenusa.
Solución
A
Sea x la longitud de la proyección
del cateto menor sobre la
hipotenusa.
Sea y la longitud de la proyección
del cateto mayor sobre la
hipotenusa.
Sea h la longitud de la altura
sobre la hipotenusa.
B
Se calcula la longitud de x .
C
Se calcula la longitud de y .
482  x  73  x 
2304
73
552  x  73  x 
3025
73
D
D
Se calcula la longitud de h .
La altura sobre la hipotenusa mide
h2 
2304 3025
2640

h
73
73
73
2640
cm .
73
3. En un triángulo rectángulo cuya hipotenusa mide 37 cm y su cateto menor
12 cm , calcule la longitud de la altura sobre la hipotenusa.
Solución
A
B
C
Sea x la longitud de la
proyección
del
cateto
menor sobre la hipotenusa,
para calcularla se aplica el
teorema del cateto.
Ahora
se
calcula
la
proyección del otro cateto.
122  x  37

144
x
37
37  x  37 
Finalmente se calcula la
longitud de la altura sobre
la hipotenusa.
h2 
144 1225

37
37
144 1225

37
37
176400
1369
420
h
37
h
E
La altura sobre la hipotenusa mide
420
cm .
37
Ejercicios
1. En la columna de la izquierda de la tabla que aparece a continuación,
encontrará ternas pitagóricas correspondientes a las longitudes de los lados
de diferentes triángulos rectángulos. Usted debe asociar cada uno de estos
triángulos rectángulos con la longitud de la altura sobre la hipotenusa en la
columna de la derecha, escribiendo la letra correspondiente dentro del
paréntesis que considera correcto. Todas las medidas están dadas en
centímetros.
A
65,72,97


660
61
B
11,60,61


240
13
C
20, 48,52


336
25
D
36,77,85


4680
97
E
14, 48,50


2772
85
2. Si en un triángulo rectángulo sus catetos miden 10 m y 24 m
respectivamente, calcular las longitudes de:
a)
b)
c)
d)
La hipotenusa.
La proyección del cateto menor sobre la hipotenusa.
La proyección del cateto mayor sobre la hipotenusa.
La altura sobre la hipotenusa.
3. Si en un triángulo rectángulo la altura sobre la hipotenusa mide 6 cm y la
proyección del cateto menor sobre la hipotenusa mide 3 cm calcular las
longitudes respectivas de:
a) La proyección del cateto mayor sobre la hipotenusa.
b) El cateto mayor.
c) La hipotenusa.
d) El cateto menor.
Soluciones
1.
En todos los casos se considera que:
x es la longitud de la proyección del cateto menor sobre la hipotenusa.
y es la longitud de la proyección del cateto mayor sobre la hipotenusa.
h es la longitud de la altura sobre la hipotenusa.
A
65,72,97
4225
97
5184
722  y  97  y 
97
4225 5184
4680
h2 

h
97
97
97

B

660
61

C

240
13

E

336
25
A

4680
97
652  x  97  x 
B
11,60,61
121
61
3600
602  y  61  y 
61
121 3600
660
h2 

h
61
61
61
112  x  61  x 
C
20, 48,52
100
13
576
482  y  52  y 
13
100 576
240
h2 

h
13 13
13
202  x  52  x 
D
36,77,85

1296
85
5929
772  y  85  y 
85
1296 5929
2772
h2 

h
85
85
85
362  x  85  x 
14, 48,50
E
98
25
1152
482  y  50  y 
25
98 1152
336
h2 

h
25 25
25

D
142  x  50  x 

2772
85
2.
A
Sea c la longitud de la hipotenusa, para calcularla se aplica el teorema
de Pitágoras:
102  242  c2
 676  c2
 26  c
La hipotenusa mide 26 m .
B
Sea x la longitud de la proyección del cateto menor sobre la
hipotenusa, para calcularla se aplica el teorema del cateto:
102  x  26
 100  x  26

50
x
13
La proyección del cateto menor sobre la hipotenusa mide
50
m.
13
C
Sea y la longitud de la proyección del cateto mayor sobre la
hipotenusa, para calcularla se aplica el teorema del cateto:
242  y  26
 576  y  26

288
y
13
La proyección del cateto mayor sobre la hipotenusa mide
D
288
m.
13
Sea h la longitud de la altura sobre la hipotenusa, para calcularla se
aplica el teorema de la altura sobre la hipotenusa:
50 288

13 13
14400
 h2 
169
120
h
13
h2 
La altura sobre la hipotenusa mide
120
m.
13
3.
A
Sea y la longitud de la proyección del cateto mayor sobre la
hipotenusa, para calcularla se aplica el teorema de la altura sobre la
hipotenusa:
62  3  y
 12  y
La proyección del cateto mayor sobre la hipotenusa mide 12 cm .
B
Sea b la longitud del cateto mayor, para calcularla se aplica el teorema
de Pitágoras:
b2  62  122
 b2  180
b6 5
El cateto mayor mide 6 5 cm .
C
Sea c la longitud de la hipotenusa, para calcularla basta con sumar las
dos proyecciones de los catetos sobre ella:
c  3  12
 c  15
La hipotenusa mide 15 cm .
D
Sea a la longitud del cateto menor, para calcularla se aplica el teorema
de Pitágoras:
a2  32  62
 a2  45
a3 5
El cateto menor mide 3 5 cm .