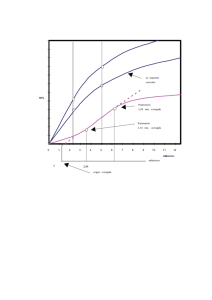
el papel de la inferencia estocástica en economía cuantitativa

El papel de la inferencia estocástica en economía cuantitativa
EL PAPEL DE LA INFERENCIA ESTOCÁSTICA EN
ECONOMÍA CUANTITATIVA
Nelson Julio Álvarez Vázquez ([email protected])
Julián Rodríguez Ruiz ([email protected])
Carlos González Salgueiro
UNED
RESUMEN
El objeto de la comunicación es poner de manifiesto los problemas derivados de la
interpretación del esquema de la inferencia estocástica.
Este esquema determinaría una alteración del objeto de la economía cuantitativa,
planteado no como la obtención de valores numéricos para las supuestas constantes económicas,
sino como la obtención de estimadores consistentes, de unos parámetros cuya existencia ni
consta ni se plantea su determinación.
Este planteamiento tiene consecuencias lógicas, como es suponer, que las series
históricas agregadas son muestras aleatorias o procesos estocásticos autocorrelacionados, y
consecuencias prácticas. Hoy, instituciones como el INE, miden las características económicas
mediante encuestas muestrales, sin que se disponga de la validación poblacional, como por
ejemplo, ocurre con los datos de empleo y paro. Otro ejemplo, son los notables fracasos
estimadores de las encuestas de opinión, pese a no poder aplicar rigurosamente los principios
de la inferencia estocástica.
En último extremo, si existió una ciencia económica racional, estableciendo
deductivamente leyes referidas a unidades individuales, la inexistencia de los correspondientes
datos, llevó la cuantificación a basarse en datos principalmente de series históricas agregadas.
La interpretación de los mismos en el esquema de la inferencia estocástica, ha supuesto un
desviacionismo de los objetos de lo que entendemos debiera ser la economía cuantitativa.
La ponencia se ilustra empíricamente con una revisión de los ensayos econométricos
tendentes a la medición de constantes como la propensión al consumo.
XII Jornadas de ASEPUMA
1
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
1. INTRODUCCIÓN
La tesis principal de la comunicación es que el papel de la inferencia estocástica en
economía cuantitativa, es decir, la econometría, no está justificado adecuadamente. Quiere ello
decir, que el supuesto de aleatoriedad aplicado a las series históricas, estaría en contradicción
con el principio de contrastación empírica. La inferencia estocástica desempeñaría el papel
principal dado que el problema estaría en inferir las características poblacionales, suponiendo
que el problema de la economía cuantitativa esencialmente es inferir.
Para apoyar reducir el problema de la economía cuantitativa a inferencia estocástica, se
precisa establecer conceptos muestrales.
Se supone (sin prueba) que los datos económicos, en particular, que las series históricas
(tipo habitual de datos en economía) pueden interpretarse en el marco de la probabilidad,
suponiendo que constituyen muestras aleatorias. Interpretadas las series históricas como
muestras aleatorias de un proceso estocástico, que desempeñaría el papel análogo a la
población, permitirían inferir los valores de los parámetros (o características de la población).
Un muestreo supone un contraste con los valores de la población objeto de inferencia.
¿Cómo podría estar un investigador seguro de que las inferencias son correctas, por ejemplo, de
que los estimadores son de hecho y en realidad consistentes, si no tiene en determinado
momento un conocimiento de la población que infiere? El proceso estocástico poblacional
siempre se considera desconocido.
Si el esquema basado en la probabilidad se considera no fundado, la comunicación no se
reduce a un mero criticismo de la hipótesis dominante, la probabilidad. Se propone una
alternativa basada en la periodicidad para medir en economía, es decir, para implementar el
objeto de la economía cuantitativa.
Si bien un economista que aspira a cuantificar necesita una respuesta al problema, por
razones de simplificar la exposición, el núcleo central de la comunicación se centra en los
criticismos a la probabilidad, cuestión no irrelevante, dado que en la estadística económica
(entre 1914 y 1938) y en la econometría desarrollada a partir de los años cuarenta, la
probabilidad no se cuestiona. La comunicación cuestiona el supuesto de que las series históricas
se adapten a los esquemas probabilísticos.
2
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
2. NOTA HISTÓRICA.
La cuestión del arraigo de la probabilidad no es independiente de la historia de la
cuantificación económica. Ya queda que dentro de la economía cuantitativa, primero existía la
estadística económica, luego la econometría. Ambas utilizan la probabilidad, la econometría
añade el recurso a la inferencia estocástica. En un principio, la ciencia económica era
cualitativa, y algunos autores, consideraban con error que la cuantificación podía verse como un
paso más en la aproximación a la ciencia económica. Como ilustra el lema de Moore, el
complemento estadístico de la economía pura (Moore, 1908), el objetivo era cuantificar lo
cualitativo. No hay tal. La economía cuantitativa, parte de los datos y los métodos, un punto de
partida diferente al esquema causal tomado de la filosofía. La economía teórica (clásica y
neoclásica) surge en el seno de la filosofía, como un planteamiento cualitativo y causal,
referido a agentes económicos individuales. Por tal puede entenderse la fundamentación de la
teoría de la demanda respecto al precio en el principio del decrecimiento de la utilidad marginal.
La utilidad solo puede predicarse de agentes económicos (consumidores) individuales. No es
medible ni en términos individuales, menos en términos agregados.
La economía cuantitativa habría surgido,
como señala Mitchell (1925), como el
resultado de la conjunción de dos factores: la aparición de datos (habitualmente agregados) y el
desarrollo de los métodos estadísticos. Los datos eran agregados (no se sabe que existan datos
individuales, ni parece verosímil que existan), y cuestiones como la denominación de datos
microeconómicos a datos de presupuestos familiares, confunden más que ilustran. En realidad,
los datos de presupuestos familiares, son datos agregados referidos a gastos y rentas de familias
en términos agregados.
Por otra parte, los métodos estadísticos, suponen válida la aplicación de la probabilidad.
Si la estadística esta asociada a la probabilidad, dado que hablaban por ejemplo de errores
probables, o de probabilidad de determinados coeficientes, en le econometría se da un paso más
al reinterpretar que la cuantificación económica debe replantearse como inferencia estocástica.
Cuando Morgan (1990) afirma que la estadística y la probabilidad se desarrollaron durante un
tiempo de forma independiente, leída sin precaución, puede inducir a error. Parece que debiera
referirse a que la estadística se habría desarrollado sin plantear la inferencia estocástica. No
cabe concebir la estadística, sin probabilidad.
La reducción de las distribuciones de
probabilidades (observaciones numerosas) a un número reducido de características (no es
necesario pensar en estimadores y parámetros, basta pensar en coeficientes), lo que permite
aplicar la idea de ciencia como determinación de regularidades. Si no existiera la ley del azar o
de estabilización de las frecuencias relativas, no tendría sentido hablar de ciencia de las
XII Jornadas de ASEPUMA
3
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
probabilidades. Es cierto que se suele hablar de método científico, pero no se explica a que se
debe esta calificación. Es un nuevo equívoco.
Uno de los ejemplos ilustrativos de la contribución a la ciencia de las probabilidades es
la representación de las estaturas de adultos de determinadas poblaciones con existencia física,
mediante números característicos como una distribución normal (α, σ). Reducir toda una
distribución de sucesos individuales a dos números como (α, σ), es abordar una análisis
científico, dado que la irregularidad de los valores individuales, se transforma en la regularidad
de tan solo dos números.
De lo contrario, la irregularidad de una distribución probabilística caería fuera de la
ciencia.
La inferencia estocástica ha cometido a nuestro juicio varios errores graves. Suponer
que las series históricas pueden ser interpretadas como muestras aleatorias. Este error es más
grave si se afirma que basta que la existencia de la población sea hipotética, (como dice
Haavelmo en su manifiesto de 1944). Puede ser hipotético que la población, objeto de
inferencia, sea infinita. Esto permite calificar la inferencia como muestreo de poblaciones
infinitas. En este sentido se habrían manifestado R. Fisher (1912) y Koopmans (1937).
Otro error es asumir que la autocorrelación sigue siendo probabilidad. Es un sin sentido
afirmar como hace Spanos (1986), que el supuesto de muestras aleatorias aplicado a series
históricas, no es realista. Predica realismo de un concepto. No cabe hablar de falta de realismo
porque no se verifique una exigencia analítica como pueda ser la falta de independencia.
Finalmente, mencionemos otro error. Tratan la no estacionaridad dentro del esquema
estocástico. El problema de las correlaciones y regresiones espurias, significaría un problema de
inferencia estocástica, sin atender a problemas de las constantes económicas cifradas
numéricamente.
Como estas cuestiones exigirían varias comunicaciones, empezamos el análisis por el
principio. Es decir, planteamos lo que sea la inferencia estocástica en sentido estricto. Por esta
expresión se entiende que :
1) debe existir un conocimiento de la población total;
2) dado este conocimiento, se infiere para otros contextos, las características de la
población, contrastando la acuracidad de las inferencias. (precisión)
4
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
Un planteamiento de inferencia estocástica se ilustra con una simulación numérica
basada en un ejemplo numérico.
DISTRIBCUIÓN HIPOTÉTICA DE FRECUENCIAS
ASIMILABLE A UNA DISTRIBUCIÓN
PROBABILÍSTICA NORMAL.
120
Series: YNRAND
Sample 1000 2000
Observations 1001
100
80
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
60
40
20
Jarque-Bera
Probability
0
-3
-2
-1
0
1
2
0.005904
0.034923
3.121613
-3.022917
1.015793
-0.062609
2.930574
0.854995
0.652139
3
figura 1
Consideremos el ejemplo de una distribución probabilística referida a una distribución
de las estaturas de sendas poblaciones humanas como pudiera ser la sueca o la china. Se habla
de dos poblaciones de estaturas, porque pueden distinguirse entre sí, por sus características
medias. Se distinguirían entre si por las estaturas medias, y /o por las respectivas desviaciones
de los valores individuales a partir de dichas medias. Como no disponemos de los datos de
ninguna de ellas, suponemos que son los valores representados en la figura 1, interpretada como
una distribución empírica de frecuencias, considerada análoga a una distribución teórica de
probabilidades como una normal.
Una distribución de frecuencias como la de la figura 1, podría representar las
respectivas distribuciones de estaturas de chinos y suecos. La distribución estaría referida a
1001 individuos (supuestamente chinos o suecos), cada uno se representaría por una media,
α= 0.006, y σ =1.02 Constituye una abstracción.
Sobre esta población se supone tomar una muestra infiriendo los valores medios
poblacionales a partir de un menor número de elementos poblacionales. La distribución
muestral que permite inferir las características poblacionales, se representa en la figura 2.
XII Jornadas de ASEPUMA
5
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
MUESTRA ALEATORIA DE LA POBLACIÓN DE
LA FIGURA 1
14
Series: YNRAND
Sample 1000 1100
Observations 101
12
10
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
8
6
4
2
Jarque-Bera
Probability
0
-3
-2
-1
0
1
-0.083236
0.023607
2.394513
-2.892656
1.116775
-0.226779
2.792976
1.046081
0.592716
2
figura 2
Implica haber seleccionado a partir de la población representada en la figura 1, una
muestra representativa (aleatoria) de 101 unidades individuales. En el supuesto de que
estuviéramos ante una población de 1001 unidades, podrían inferirse los valores de media y
varianza a partir de una muestra de 101.
Esta afirmación se ilustra en la figura 2. Existe una pequeña diferencia entre las
características de la muestra y de la población: ahora α = - 0.08, que sería la media poblacional,
siendo la media de la muestra, 0.005. En forma análoga, se inferiría una desviación poblacional
de σ =1.12, a partir de una desviación
muestral de 1.02. Las diferencias entre valores
poblacionales y muestrales podrían imputarse a errores de muestreo, es decir, al proceso de
realizar una inferencia, puesto que sabemos que la muestra ha sido seleccionada a partir de la
población..
Es importante constatar que las figuras 1 y 2, son atemporales, es decir, no contemplan
el tiempo, sino que relacionan valores (por ejemplo entre –3 y +3) y frecuencias. Es decir , la
inferencia estocástica es atemporal, no estando pensada para ser aplicada a series históricas, es
decir, observaciones con dimensión temporal. El paso de lo atemporal a lo temporal, supone un
salto lógico que debe ser justificado. Un planteamiento basado en series históricas, difiere de un
planteamiento causal (por ejemplo, psicológico, como el adoptado en un principio en
economía), en que los datos son agregados y en particular series históricas (con dimensión
temporal).
De hecho en la inferencia estocástica supone que este salto lógico, se resuelve
fácilmente generalizando la noción de variable aleatoria atemporal a una variable aleatoria
temporal, que se denomina proceso estocástico.
6
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
Una ilustración de este supuesto puede encontrarse en la siguiente cita referida a la
Political Arithmetic, afirmando que series históricas o transformaciones de determinadas series
como ratios, se comportaban como distribuciones atemporales referidas a agregados como las
observadas en la figura 1: “La constatación de que la estadística podría servir como método de
ataque de la mayor parte de los problemas sociales... se debe a Graunt. Estudió por curiosidad
las series de fallecidos en las ciudades inglesas, notando que los porcentajes de fallecidos
debidos a accidentes, suicidios y otras enfermedades eran aproximadamente los mismos año a
año en las localidades estudiadas. Estos sucesos que se atribuían al azar poseían una regularidad
sorprendente... El trabajo de Graunt fue seguido y apoyado por su amigo Sir William Petty...
llama la atención sobre el método de la estadística. Insistía en que las ciencias sociales debían
ser cuantitativas... contempló la economía política como una rama de la estadística” (Kline , p.
500, 1967).
Esta regularidad, que sirve para fundamentar el tratamiento de la economía cuantitativa
mediante la inferencia estocástica es lo que se cuestiona en la comunicación. Los ratios ni
demográficos ni económicos, no se comportarían de acuerdo a regularidades probabilísticas.
Puede que existan otro tipo de regularidades pero cuestionamos que sean las probabilísticas.
Tal conclusión ha de tenerse como de valor particular, dado que la prueba se basa en
ejemplos particulares. No afirma que no existan regularidades, sino que las regularidades
existentes, no son las utilizadas en el cálculo de probabilidades.
No es posible analizar todos los casos, pero sería de interés que quienes asumen la
inferencia estocástica, presentaran evidencias al respecto. Se analiza en los dos siguientes
epígrafes, ejemplos de ratios demográficos y económicos.
3. EL ESTUDIO DE DOS RATIOS DEMOGRÁFICOS REFERIDOS
A LA POBLACIÓN ESPAÑOLA.
El problema se ilustra con datos de la población española, es decir, con los ratios de
nacidos y fallecidos. Se calculan los ratios respectivos de nacidos y fallecidos, como cocientes
de los respectivos números de nacidos y fallecidos entre la población total. Los datos básicos se
reproducen al final de la comunicación.
XII Jornadas de ASEPUMA
7
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
RATIOS DE NACIDOS Y FALLECIDOS DE
LA POBLACIÓN ESPAÑOLA
4
4
3
3
2
2
1
1
0
RNAC
RDEF
0
1875
1900
1925
1950
1975
figura 3
Se representan ambos ratios en la figura 3. No se prejuzga que el empleo de ratios en
economía sea adecuado. Se asume que ha sido un procedimiento utilizado con profusión. En la
comunicación, se sugiere más delante, que existen otras alternativas que se consideran
preferibles.
Para el objeto de establecer la no regularidad, solo se analiza la trayectoria, primero en
tiempo, luego en forma atemporal.
Se puede concluir a partir de la evidencia de la figura 3, que ambos ratios demográficos
registran tendencias decrecientes, a las que se superponen fluctuaciones. No presentarían un
valor estable en el tiempo. Lo cual se interpreta una consecuencia de que los datos sean series
históricas.
Para interpretarlos dentro del esquema probabilístico, se considera que una
posibilidad es prescindir de la dimensión temporal.
8
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
DISTRIBUCIÓN DE FRECUENCIAS
DEL RATIO DE NACIDOS.
24
Series: RNAC
Sample 1858 1990
Observations 133
20
16
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
12
8
4
Jarque-Bera
Probability
0
1.0
1.5
2.0
2.5
3.0
3.5
2.756061
2.897499
3.917675
1.016464
0.817753
-0.358788
1.908434
9.456475
0.008842
4.0
figura 4
Consideremos el ratio de nacidos. Si se prescinde de su dimensión temporal, se
observa (figura 4) que ya no posee las características estrictas de una población normal. No
existe una media sino varias, por no mencionar el problema de las desviaciones. El problema
es que la media, 2.76, ya no es representativa. Se observa que la distribución de frecuencias
tiene las mayores frecuencias entre 2-2.2 (una posible media), 2.8-3 (otra posible media) y 3.53.7 (otra posible media). El hecho de que existan diferentes medias, se interpreta como una falta
de homogeneidad, como una ausencia de regularidad. Es como si en la población de alturas de
suecos o chinos hubiera varias alturas medias. Este resultado no se podría distinguir de otro
derivado de construir una distribución con las estaturas de ambas poblaciones. No tendría
sentido pensar en representar semejante población física mediante una población estadística
normal, con tan solo dos características.
Evidencia que sugiere la no plausibilidad de ensayar un proceso de inferencia. Inferir
media o varianza carecería de sentido, dado que no existiría una única media o varianza.
Existiendo varias medias no podría hablarse de una sola, si bien el problema resulta
enmascarado porque no se contrasta media muestral y poblacional.
Este hallazgo parece coherente con las evidencias encontrado por algunos estadísticos al
calcular las distribuciones de frecuencias (atemporales) de estadísticos como el coeficiente de
correlación. El problema siendo diferente se basa en un razonamiento similar. Si la distribución
atemporal de frecuencias de un coeficiente de correlación no era unimodal, se consideraba
insatisfactorio tratar tales coeficientes de correlación mediante una inferencia estadística como
la desarrollada para medias.
XII Jornadas de ASEPUMA
9
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
DISTRIBUCIÓN DE FRECUENCIAS
DEL RATIO DE FALLECIDOS
30
Series: RDEF
Sample 1858 1990
Observations 133
25
20
15
10
5
0
1.0
1.5
2.0
2.5
3.0
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
1.979667
1.951153
3.796687
0.755766
0.929592
0.025805
1.488601
Jarque-Bera
Probability
12.67375
0.001770
3.5
figura 5
La figura 5 ilustra que esta evidencia no es singular ni episódica, dado que cabe realizar
las mismas observaciones en relación con el ratio de fallecidos. Aparecen varias medias, no una
sola, de manera que no parece natural pensar en representar la distribución del ratio por una sola
media.
La existencia de varias medias, es coherente con las tendencias decrecientes de la figura
3.
Si se dispusiera de evidencias diferentes, sería preciso aportarlas como paso previo a
aplicar la inferencia estocástica. No cabe negar que la cuestión se deba a un menor número de
observaciones.
DISTRIBUCIÓN DE FRECUENCIAS
DERIVADA DE UNA NORMAL
20
Series: YNRAND
Sample 1858 1990
Observations 133
16
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
12
8
4
Jarque-Bera
Probability
0
-3
-2
-1
0
1
-0.012328
-0.004753
2.156000
-2.868517
1.012430
-0.152685
2.971903
0.521141
0.770612
2
figura 6
Como podría alegarse que el número de observaciones en el caso de los dos ratios, es
menor 133, frente a 1001, en la figura 6 se ilustra como hubiera una distribución de frecuencias
10
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
(atemporal), generada partir de una distribución teórica normal, para este mismo número. Se
comprende la importancia que estadísticos como K. Pearson, Yule o Kendall atribuían a que las
distribuciones derivadas de coeficientes de correlación o regresión (en este caso, de la razón) no
fueran unimodales. Ahora la distribución aleatoria es normal, con características similares a las
obtenidas en la figura 1. El problema no parece estar en el tamaño.
Esta evidencia no es predicable tan solo de los ratios demográficos. También se
descubre en los ratios económicos, cuestión que ya en su día preocupó a prestigiosos
económetras como Klein..
4.
LA
INESTABILIDAD
ESTADÍSTICA
DE
LOS
RATIOS
ECONÓMICOS.
Este problema fue tratado por Klein y Kosobud. Los economistas, aceptando tal vez las
ideas de Graunt y Petty, pretendían trabajar con ratios no ya demográficos, sino económicos.
Su enfoque no es el de la presente comunicación. Aceptan la plausibilidad de la
inferencia estocástica, como instrumento para juzgar la validez de los mismos. Klein y
Kosobud, aceptan o rechazan tendencias en los ratios acordes con la t de Student, que asume la
inferencia estocástica.
RATIOS DE CONSUMO/RENTA, DINERO/RENTA
Y CAPITAL /PRODUCTO
RKY
RCASH
10
RCO
8
6
4
4
2
3
0
2
1
0
-1
-2
00
05
10
15
20
25
30
35
40
45
50
figura 7
La figura 7 ilustra las trayectorias temporales de tres de los diversos ratios considerados
por los autores. Pone de relieve que mientras el ratio de capital producto (línea continua)
XII Jornadas de ASEPUMA
11
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
registra una trayectoria similar a la de los ratios demográficos, los otros dos (líneas discretas)
registrarían tendencias crecientes con fluctuaciones.
Los economistas han discutido si la
propensión al consumo era más estable (keynesianos) que la velocidad de circulación del dinero
(monetaristas). Está claro que el problema importante no era este, sino la propia existencia de
estas características agregadas referidas a un mercado concreto en el espacio (USA y en el
tiempo, 1900-1953). Las trayectorias discretas representarían las propensiones a consumir y la
velocidad de circulación del dinero, revelando tendencias crecientes con fluctuaciones.
DISTRIBUCIÓN DE FRECUENCIAS DEL
RATIO CAPITAL PRODUCTO
12
Series: RKY
Sample 1900 1953
Observations 54
10
8
6
4
2
0
2
3
4
5
6
7
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
4.540892
3.971576
8.022561
1.577765
1.916092
0.230253
1.798219
Jarque-Bera
Probability
3.726772
0.155146
8
figura 8
Las mismas series se representan en forma atemporal en las siguientes figuras. La
figura 8 representa la distribución de frecuencias del primero de los ratios económicos, el de
capital producto. Los hallazgos con los ratios económicos son similares a los derivados de los
ratios demográficos. Lo cual es una regularidad.
Es obvio que no hay una sola media sino varias.
DISTRIBUCIÓN DE FRECUENCIAS
DEL RATIO CONSUMO/RENTA
14
Series: RCO
Sample 1900 1953
Observations 54
12
10
8
6
4
2
0
0.85
0.90
0.95
1.00
1.05
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
0.915323
0.900292
1.116838
0.839674
0.062526
1.296618
4.816577
Jarque-Bera
Probability
22.55586
0.000013
1.10
figura 9
12
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
La figura 9 representa el segundo de los ratios, el de consumo/ renta. Representaría una
posible medición de la propensión media al consumo. Parece que tampoco cabe considerar que
se pueda representar por una sola media. ¿Cualquier inferencia de una media llevaría a error?.
DISTRIBUCIÓN DE FRECUENCIAS
DEL RATIO CONSUMO/RENTA
14
Series: RCO
Sample 1900 1953
Observations 54
12
10
8
6
4
2
0
0.85
0.90
0.95
1.00
1.05
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
0.915323
0.900292
1.116838
0.839674
0.062526
1.296618
4.816577
Jarque-Bera
Probability
22.55586
0.000013
1.10
figura
figura 910
La figura 10 representa la distribución de frecuencias del tercero de los ratios, que
podría interpretarse como una medición de la velocidad del dinero con respecto a la renta.
DISTRIBUCIÓN GENERADA A PARTIR
DE UNA DISTRIBUCIÓNLEATORIA
NORMAL
10
Series: YNRAND
Sample 1900 1953
Observations 54
8
Mean
Median
Maximum
Minimum
Std. Dev.
Skewness
Kurtosis
6
4
2
Jarque-Bera
Probability
0
-2
-1
0
1
0.095908
-0.007052
2.165405
-1.868732
1.027008
0.156625
2.343246
1.191266
0.551214
2
figura 11
Los tres ejemplos revelan que los tipos de distribuciones difieren de una distribución
aleatoria normal. Una ilustración de cómo sería esta se representa para la misma historia (los
mismos 54 años) en la figura 11. Como el número de observaciones es menor, se comprende
que la idea de una sola media resulte menos clara.
De todo lo anterior se desprende la no validez de la conclusión de la Political
Arithmetic, de que a las series históricas (agregadas) sea aplicable sin más la probabilidad o la
inferencia estocástica. No parece aceptable ni para los ratios demográficos ni para los
económicos, concluir acerca de la existencia de una ley estadística o de probabilidades.
XII Jornadas de ASEPUMA
13
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
DISTRIBUCIÓN ALEATORIA NORMAL
EN EL TIEMPO Y RATIOS
YNRAND
RCO
RKY
RCASH
3
2
1
0
4
-1
3
-2
2
1
0
-1
-2
00
05
10
15
20
25
30
35
40
45
50
figura 12
Los estadísticos matemáticos, es decir, los económetras, no realizan (con los datos
económicos) este tipo de análisis atemporal, sino que lo realizan en el tiempo. Sus
planteamientos se ilustran en la figura 12. En la parte superior (en barras) se representa en el
tiempo la misma distribución atemporal de la figura 11, que se compara con los tres ratios
económicos.
Lo cual implica el salto lógico, ya mencionado de predicar en el tiempo, lo que se ha
construido para el dominio atemporal. Equivale a suponer que se puede establecer una
correspondencia en el tiempo con las distribuciones de frecuencias (probabilidades)
atemporales, similar a la correspondencia observada en las series históricas. No cabe término
medio. O las distribuciones de probabilidades se proyectan en el tiempo, o las series históricas
se contemplan sin tiempo, o se asume que el salto lógico de lo atemporal a lo temporal es
legítimo. La correspondencia establecida entre aleatoriedad y tiempo, es un salto lógico que se
supone legitimado con la teoría de los procesos estocásticos. El análisis se plantea en estos
términos, generalizando a priori la idea de variable aleatoria al tiempo, dando lugar al concepto
de proceso estocástico. Ponemos en duda que este, planteamiento, esté adecuadamente fundado.
Se realiza pero no nos consta que se haya fundamentado.
No parece que se pueda invocar el principio de analogía y afirmar que los ratios puedan
considerarse suficientemente próximos a una distribución de probabilidades. Las diferencias son
claras.
14
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
COMPARACIÓN DE LA SERIE DE DINERO
EN CAJA( transformada en estacionaria) y la serie
aleatoria normal
YNRAND
DLCASH
3
2
1
0
-1
4
-2
2
0
-2
-4
00
05
10
15
20
25
30
35
40
45
50
figura 13
Ahora bien, la analogía no se establece en términos atemporales. Se procede analizando
en el tiempo, si la serie económica es o no estacionaria. Se suele aplicar transformaciones de los
datos originales como primeras diferencias o tasas de variación, lo que se ilustra en la figura 13.
Ahora se aplica a la cantidad de dinero, no al ratio, porque entendemos el empleo de un ratio
como discutible. No se puede afirmar que, porque la serie transformada sea aparentemente
estacionaria, se pueda considerar análoga a una distribución de probabilidades, supuesto que
fuera admisible establecer su correspondencia en el tiempo. La comparación con la serie
aleatoria representada en la parte superior de la figura 13, revela la inaplicabilidad del
argumento de analogía.
El problema solo se ha planteado en su principio, dado que habría que entrar en
cuestiones como procesos estacionarios autocorrelacionados en el tiempo, y procesos no
estacionarios.
Ahora bien, el reconocimiento de su existencia favorece el argumento de la
inaplicabilidad de la probabilidad a las series históricas.
5. CONCLUSIÓN: LA INFERENCIA ESTOCÁSTICA EN SERIES
DE TIEMPO O LA PERIODICIDAD.
Se infiere de lo anterior que no parece justificado aplicar a datos de series históricas los
principios del cálculo de probabilidades, y en consecuencia, de la propia inferencia estocástica,
pese a que la inferencia estocástica y los datos económicos sean agregados. Es decir, si la
XII Jornadas de ASEPUMA
15
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
distribución de frecuencias de un ratio no posee características únicas, no tiene sentido asumir
que el problema se reduce a evitar inferencias espurias, como se supone a lo largo de toda la
econometría. No tiene sentido practicar inferencias mediante muestreos aleatorios, aplicados a
series históricas o a sus transformadas.
Llevaría demasiado tiempo y espacio, entrar en otras cuestiones como la no
estacionaridad, cuestión que se deja para otra comunicación. Solo se anticipa, una cuestión que
merece un estudio propio, interpretar las magnitudes económicas de acuerdo a la hipótesis
alternativa. Es decir, las regularidades no serían estocásticas, pero podrían ser determinísticas.
DINERO, CONSUMO Y CAPITAL:
ciclos empíricos
2
CLK
CLCO
CLCASH
1
0
-1
-2
-3
00
05
10
15
20
25
30
35
40
45
50
figura 14
Se anticipa una ilustración en la figura 14: representa los ciclos empíricos de las tres
variables económicas agregadas, utilizadas en los numeradores de los ratios, que resultan de ser
sometidas a una transformación diferente a los ratios. Se habrían eliminado sendas tendencias
exponenciales por los extremos de las series. Desde un punto de vista formal, pone de
manifiesto la tesis de no trabajar con ratios, contemplando alternativamente estudiar los
fenómenos en cuanto tales. Si ciencia es poner de manifiesto, tanto en términos cualitativos
(análisis causal) como cuantitativos (análisis cíclico), la existencia de regularidades, estas se
encontrarían en los ciclos empíricos (series históricas observadas, libres de tendencias), no en
las aproximaciones probabilísticas, cuyas regularidades son diferentes a las obtenidas de la ley
del azar, construidas conceptualmente para problemas como los juegos de azar.
A favor de los ciclos cabe aducir regularidades comunes como la depresión de 1929
(evidente y señalada en los tres ciclos), y en contra de una hipótesis cíclica, la no coincidencia
16
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
de otros ciclos. Esta insatisfacción se explicará en su momento por el carácter agregado de los
datos, que sin duda no puede traducirse literalmente en regularidades en términos individuales.
Como las series son agregadas, no cabe esperar que las periodicidades se manifiesten en estado
puro.
Una razón adicional favorable a la periodicidad, como alternativa a la probabilidad
estaría en que sería posible intentar reconstruir el ciclo empírico mediante la suma de los ciclos
periódicos fundamentales.
CONSUMO: ciclo empírico y
suma de ciclos periódicos
3
CO_C
2
CONSUMOC
1
0
-1
-2
-3
00
05
10
15
20
25
30
35
40
45
50
figura 15
La evidencia de semejante intento se ilustra para el ciclo empírico de la serie de
consumo en la figura 15. Se puede constatar que el ciclo empírico puede ser aproximado
mediante la superposición de los ciclos periódicos más importantes. Existen etapas en que se
aproxima razonablemente como desde la gran depresión de 1929 hasta 1945 y etapas en las que
se aproxima mal como entre 1900 y 1905 o de 1950 en adelante. Evidencias similares
explicarían que una parte importante de economistas hayan sido adversos a la periodicidad. Es
ante todo una aproximación mecanicista, que debería saber el significado económico de cada
ciclo periódico. Lo cual pone de manifiesto que el adoptar una hipótesis como la periodicidad
exige un trabajo nada desdeñable. Pero entendemos que evitaría los inconvenientes de la
simplificación probabilística de suponer que los datos económicos (agregados de
series
históricas), verifican los requisitos de la probabilidad.
Se pone de relieve asimismo la futilidad de los análisis macroeconómico basados en
datos agregados, así como la dificultad de establecer un nexo con los planteamientos
individuales, atemporales. Por ejemplo, en términos individuales se habla de una función de
XII Jornadas de ASEPUMA
17
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
bienestar no medible que luego se postula en términos agregados como una función de bienestar
social. ¿Tiene este planteamiento justificación alguna?. Entendemos que la respuesta ha de ser
negativa.
Si una ciencia como la economía o la sociología ha de basarse en datos agregados (la
psicología se basaría en datos individuales, de los que no disponemos en economía), se requiere
ir a los principios estableciendo los fundamentos, cuestión que no se ha hecho ni parece que se
pretenda abordar.
La conclusión es clara: la inferencia estocástica, la probabilidad, no parece aplicable en
economía, salvo que se justifique más fehacientemente, siendo preciso pensar en nuevas formas
de establecer las regularidades. El objeto de toda ciencia es la formulación de regularidades. La
afirmación de la Political Arithmetic no parece que fuere correcta. No parece trasladable a la
economía el supuesto de que sus fenómenos se rijan por la ley estadística. Si la inferencia
estocástica no es trasladable a los hechos económicos, no tiene sentido todo el desarrollo actual
de la econometría. Volveríamos a los principios, cuestión sobre la que se había pronunciado
Schultz en su obra magna de 1938, pese que había mantenido conversaciones un año antes en
Chicago con Neyman. Entendía que la inferencia estocástica no era aplicable a las series
históricas.
Esta comunicación constituye una señal de alerta para los matemáticos. Sin duda están
llamados a realizar grandes progresos a la ciencia económica, si bien entendemos que si la
presente comunicación no estuviera en el error, derivarían de otros esquemas. Es posible que su
contribución a la economía cuantitativa fuera más fecunda por otras vías que no las actuales de
la probabilidad. Con esta intención se presenta.
Obs
1900
1901
1902
1903
1904
1905
1906
1907
1908
1909
1910
1911
1912
1913
1914
1915
1916
1917
18
CO
27.80000
30.50000
30.90000
32.90000
33.30000
34.90000
38.30000
39.70000
38.10000
41.40000
42.10000
43.20000
42.80000
44.70000
47.10000
48.20000
49.40000
50.80000
CASH
8.900000
10.00000
10.80000
11.50000
12.00000
13.20000
14.10000
15.10000
14.70000
15.80000
17.00000
17.80000
18.90000
19.40000
20.00000
20.70000
24.20000
28.20000
K
131.5700
136.7100
142.2700
147.7900
152.2000
157.6500
164.5000
171.2500
175.3100
182.0500
187.8600
192.4500
198.0400
204.3800
207.2800
210.3600
215.7000
220.2600
Y
YNRAND
16.40000 1.028946
18.00000 0.572408
18.80000 -0.011362
20.00000 1.698631
19.90000 -1.662477
21.70000 -0.148062
24.80000 1.267818
26.50000 1.060347
24.10000 -1.072211
28.10000 -0.741237
29.00000 -1.591245
28.60000 0.212290
30.20000 -1.640846
32.10000 -0.111777
31.60000 -0.384977
35.20000 -0.742059
43.50000 -0.963588
53.90000 2.041558
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
1918
1919
1920
1921
1922
1923
1924
1925
1926
1927
1928
1929
1930
1931
1932
1933
1934
1935
1936
1937
1938
1939
1940
1941
1942
1943
1944
1945
1946
1947
1948
1949
1950
1951
1952
1953
49.60000
52.20000
54.20000
57.00000
59.20000
64.30000
69.00000
67.10000
72.50000
74.20000
76.30000
80.30000
75.90000
73.20000
66.40000
65.00000
68.60000
73.10000
80.80000
84.40000
83.00000
87.00000
91.70000
97.90000
96.20000
98.80000
102.2000
109.1000
122.3000
124.0000
127.5000
130.7000
138.7000
139.8000
143.9000
149.4000
31.40000
35.60000
39.90000
37.80000
39.00000
42.70000
44.50000
48.30000
50.60000
52.20000
54.70000
55.20000
54.40000
52.90000
45.40000
41.70000
46.00000
49.90000
55.10000
57.30000
56.60000
60.90000
67.00000
74.20000
82.00000
110.2000
136.2000
162.8000
171.2000
165.5000
167.9000
167.9000
173.8000
181.0000
191.0000
197.6000
223.9400
229.3700
235.1300
236.1900
240.1500
248.8700
254.4700
264.0800
273.9400
282.6100
290.2000
299.4200
303.3000
303.4200
297.1200
290.1200
285.4300
287.7800
292.1100
300.3300
301.3800
305.5800
313.3200
327.4200
338.9800
347.0800
353.4600
354.1300
359.4300
359.3000
365.1900
363.2100
373.7300
385.9500
396.4700
408.0100
58.20000
65.20000
75.70000
61.80000
63.00000
74.10000
75.20000
78.60000
84.60000
83.10000
85.00000
90.30000
76.90000
61.70000
44.80000
42.60000
50.30000
58.20000
68.30000
75.10000
68.80000
73.80000
81.80000
99.00000
106.5000
113.2000
118.7000
124.2000
160.5000
179.0000
192.8000
185.8000
215.0000
238.1000
245.6000
258.6000
-1.040384
-0.002742
0.034989
-1.291358
1.345884
1.203483
0.211318
-1.868732
2.165405
-0.234004
-1.041302
-0.403777
1.632333
-0.335921
0.181280
-0.138619
0.558888
0.301718
1.151971
0.028665
0.455505
0.140993
1.404914
0.895506
-0.323918
-0.183598
-1.402977
-0.311138
0.835878
0.214991
-0.075041
-0.582028
-0.204288
1.780360
-0.677944
1.940556
Tabla 1: datos primarios económicos.
La tabla 1 reproduce los datos primarios con los que se han obtenido los ratios y ciclos
económicos.
obs
1858
1859
1860
1861
1862
1863
1864
1865
1866
1867
1868
1869
1870
1871
1872
XII Jornadas de ASEPUMA
NACIM
546.2000
559.0000
573.5000
611.6000
607.1000
598.1000
621.5000
614.9000
611.7000
617.5000
574.2000
596.7000
593.6000
594.5880
595.5750
DEFUN
433.9000
449.0000
429.0000
417.8000
430.7000
461.7000
499.5000
538.6000
463.7000
487.2000
548.7000
550.6000
512.2000
511.6750
511.1500
POB YNRAND
15526.00 -0.970368
15584.00 -0.380342
15645.00 -0.829012
15699.00 0.667646
15754.00 -0.095637
15809.00 1.072001
15864.00 0.026987
15920.00 1.698626
15976.00 1.712533
16032.00 -1.076502
16088.00 -1.783181
16144.00 -0.247286
16201.00 1.086044
16258.00 -1.125075
16315.00 2.156000
19
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
1873
1874
1875
1876
1877
1878
1879
1880
1881
1882
1883
1884
1885
1886
1887
1888
1889
1890
1891
1892
1893
1894
1895
1896
1897
1898
1899
1900
1901
1902
1903
1904
1905
1906
1907
1908
1909
1910
1911
1912
1913
1914
1915
1916
1917
1918
1919
1920
1921
1922
1923
1924
1925
1926
1927
1928
1929
1930
1931
1932
20
596.5630
597.5500
598.5380
599.5250
600.5130
601.5000
601.1000
598.2000
629.6000
617.0000
610.7000
631.8000
629.0000
638.2000
631.8000
640.2000
647.6000
615.5000
632.9000
645.4000
644.9000
632.5000
636.1000
654.8000
625.2000
612.3000
632.6000
627.8000
650.6000
666.7000
685.3000
649.9000
670.7000
650.4000
646.4000
658.0000
650.5000
647.0000
628.4000
637.9000
617.9000
608.2000
614.8000
599.0000
602.1000
612.6000
586.0000
623.3000
648.9000
656.1000
662.6000
653.1000
644.7000
663.4000
636.0000
666.2000
653.7000
660.9000
649.3000
670.7000
510.6250
510.1000
509.5750
509.0500
508.5250
508.3000
511.5000
507.3000
511.8000
534.9000
559.6000
526.5000
657.7000
509.6000
573.4000
529.5000
545.1000
577.5000
566.0000
554.3000
541.1000
556.1000
527.2000
539.1000
520.2000
518.8000
533.1000
536.7000
517.6000
488.3000
470.4000
486.9000
491.4000
499.0000
472.0000
460.9000
466.6000
456.2000
466.5000
426.3000
449.3000
450.3000
452.5000
441.7000
465.7000
695.8000
482.8000
494.5000
455.5000
441.3000
449.7000
430.6000
432.4000
420.8000
419.8000
413.0000
407.5000
394.5000
409.0000
388.9000
16372.00
16429.00
16487.00
16545.00
16603.00
16677.00
16768.00
16859.00
16951.00
17043.00
17136.00
17230.00
17323.00
17418.00
17513.00
17600.00
17678.00
17757.00
17838.00
17916.00
17996.00
18076.00
18157.00
18238.00
18320.00
18402.00
18484.00
18566.00
18659.00
18788.00
18919.00
19050.00
19133.00
19316.00
19450.00
19585.00
19721.00
19927.00
19994.00
20128.00
20163.00
20398.00
20535.00
20673.00
20811.00
20950.00
21091.00
21303.00
21411.00
21628.00
21847.00
22069.00
22292.00
22518.00
22747.00
22977.00
23210.00
23445.00
23675.00
23897.00
1.840466
-0.545589
0.517078
2.024271
-0.808768
0.137919
1.350950
-0.121908
-1.066095
-0.016284
0.246250
-0.450359
-0.195898
0.985587
0.455489
-0.623361
0.479372
0.728582
-0.059752
0.384043
0.790738
-0.030403
-0.265609
-0.801705
-1.534874
-1.951160
0.015094
1.889014
1.254628
0.319998
-0.781221
-0.811135
0.880645
0.149668
0.014967
-1.593626
0.670003
-1.462733
-0.188558
-0.721768
0.680013
0.579964
-0.419657
0.260355
-2.868517
-1.363958
-1.658166
0.352602
1.111136
-0.681826
-0.064651
-0.090149
-1.378568
-1.321562
0.634513
-0.189781
0.033808
-2.592369
0.096385
0.499979
XII Jornadas de ASEPUMA
El papel de la inferencia estocástica en economía cuantitativa
1933
1934
1935
1936
1937
1938
1939
1940
1941
1942
1943
1944
1945
1946
1947
1948
1949
1950
1951
1952
1953
1954
1955
1956
1957
1958
1959
1960
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
1972
1973
1974
1975
1976
1977
1978
1979
1980
1981
1982
1983
1984
1985
1986
1987
1988
1989
1990
667.9000
637.9000
632.5000
613.7000
565.8000
506.1000
419.8000
627.8000
507.8000
527.7000
603.4000
598.7000
618.0000
578.9000
582.1000
634.9000
595.1000
559.0000
561.2000
586.3000
582.7000
571.6000
592.2000
601.5000
639.5000
646.2000
647.2000
654.5000
645.6000
649.7000
662.5000
688.7000
667.7000
661.7000
672.0000
659.7000
658.9000
656.1000
664.8000
665.6000
666.3000
682.0000
669.4000
677.5000
656.4000
636.9000
602.0000
571.0000
531.9000
515.7000
485.4000
473.3000
456.3000
434.5000
421.1000
415.8000
404.6000
396.3600
394.8000
388.8000
384.6000
413.6000
472.1000
484.9000
470.1000
424.9000
484.4000
384.7000
349.0000
345.7000
327.0000
348.1000
325.3000
299.8000
316.3000
301.0000
322.3000
271.7000
273.6000
259.9000
269.3000
285.5000
289.6000
255.9000
264.5000
262.3000
256.4000
271.4000
275.5000
267.0000
267.4000
269.7000
274.0000
277.4000
297.2000
280.2000
302.9000
280.2000
296.5000
295.3000
298.2000
299.0000
294.3000
296.8000
291.2000
289.3000
293.4000
286.7000
302.6000
299.4000
312.5000
306.6000
309.4000
318.8000
324.8000
330.9590
24122.00
24349.00
24579.00
24810.00
25043.00
25279.00
25517.00
25757.00
25979.00
26182.00
26387.00
26594.00
26802.00
27012.00
27223.00
27437.00
27651.00
27868.00
28086.00
28332.00
28571.00
28812.00
29056.00
29301.00
29548.00
29798.00
30049.00
30303.00
30592.00
30917.00
31246.00
31578.00
31913.00
32253.00
32595.00
32942.00
33292.00
33646.00
33983.00
34312.00
34646.00
35003.00
35515.00
35937.00
36367.00
36778.00
37108.00
37542.00
37654.00
37935.00
38172.00
38342.00
38542.00
38667.00
38757.00
38852.00
38924.00
38994.00
-0.978800
-0.185012
0.076987
-0.004753
0.247562
-1.259143
-0.165208
-0.479784
0.819782
0.179498
0.259606
0.640550
1.395718
-0.224252
0.135476
1.128284
0.292984
-0.464012
-0.320656
-0.628310
1.176381
0.140347
1.083592
-1.441113
-0.411666
-2.556366
-0.958871
1.760021
1.761774
0.018738
-1.364497
0.434186
1.392626
0.142325
-0.696876
0.601266
-0.038771
0.817797
-1.164778
-0.170185
-0.644849
-0.723987
-0.956370
0.227442
1.647711
2.083854
0.686449
-0.381726
-0.030425
0.672777
-0.196028
0.528111
1.689542
-0.581151
-1.629447
-1.308540
0.696058
0.952630
Tabla 2. datos primarios demográficos.
XII Jornadas de ASEPUMA
21
Nelson Julio Álvarez, Julián Rodríguez Ruiz, Carlos González Salgueiro.
La tabla 2 reproduce los datos utilizados para calcular los ratios demográficos. Con
unos y otros es posible reproducir los resultados que han servido de fundamento para las
conclusiones establecidas.
6. REFERENCIAS BIBLIOGRÁFICAS
•
FISHER, R. (1922): On the Mathematical Foundations of Theoretical Statistics.
Philosophical Transactions, A., CCXXII, p. 309.
•
KLEIN, L. R. and KOSOBUD, R. F. (1961): Some Econometrics of Growth: Great Ratios
of Economics. The Quarterly Journal of Economics, LXXV, 2, pp. 173-198.
•
KLINE, M. (1967): Mathematics for the Non Mathematicians. Dover Publications
Inc. New York.
•
KOOPMANS, T. C. (1937): Linear Regression Analysis of Economic Time Series.
Netherlands Economics Institute. Netherlands.
•
MITCHELL, W. C. (1925): Quantitative Analysis in Economic Theory. The American
Economic Review, XV, 1, pp. 1-12.
•
MOORE, H. L (1908): Statistical Complement of Pure Economics. Quarterly Journal of
Economics, XXIII, pp. 1 - 33.
•
MORGAN, M. S. (1990): The History of Econometric Ideas. Cambridge University
Press. Cambridge.
•
SCHULTZ, H. L. (1938): The Theory and Measurement of Demand. The University
of Chicago Press. Chicago.
22
XII Jornadas de ASEPUMA