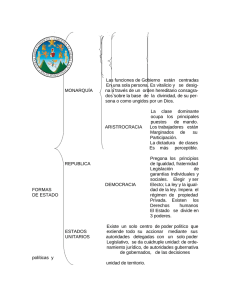
planificación

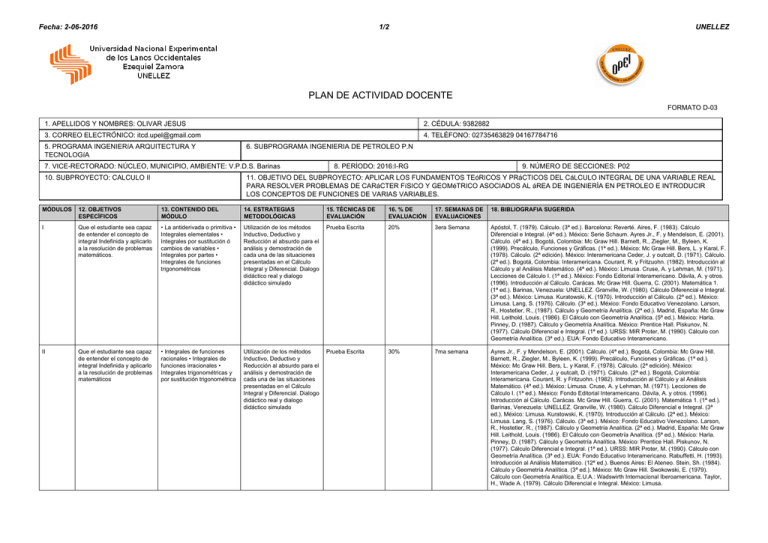
Fecha: 2-06-2016
1/2
UNELLEZ
PLAN DE ACTIVIDAD DOCENTE
FORMATO D-03
1. APELLIDOS Y NOMBRES: OLIVAR JESUS
2. CÉDULA: 9382882
3. CORREO ELECTRÓNICO: [email protected]
5. PROGRAMA INGENIERíA ARQUITECTURA Y
TECNOLOGíA
4. TELÉFONO: 02735463829 04167784716
6. SUBPROGRAMA INGENIERIA DE PETROLEO P.N
7. VICE-RECTORADO: NÚCLEO, MUNICIPIO, AMBIENTE: V.P.D.S. Barinas
10. SUBPROYECTO: CALCULO II
8. PERÍODO: 2016:I-RG
9. NÚMERO DE SECCIONES: P02
11. OBJETIVO DEL SUBPROYECTO: APLICAR LOS FUNDAMENTOS TEóRICOS Y PRáCTICOS DEL CáLCULO INTEGRAL DE UNA VARIABLE REAL
PARA RESOLVER PROBLEMAS DE CARáCTER FíSICO Y GEOMéTRICO ASOCIADOS AL áREA DE INGENIERÍA EN PETROLEO E INTRODUCIR
LOS CONCEPTOS DE FUNCIONES DE VARIAS VARIABLES.
MÓDULOS
12. OBJETIVOS
ESPECÍFICOS
13. CONTENIDO DEL
MÓDULO
14. ESTRATEGIAS
METODOLÓGICAS
15. TÉCNICAS DE
EVALUACIÓN
16. % DE
EVALUACIÓN
17. SEMANAS DE
EVALUACIONES
18. BIBLIOGRAFIA SUGERIDA
I
Que el estudiante sea capaz
de entender el concepto de
integral Indefinida y aplicarlo
a la resolución de problemas
matemáticos.
• La antiderivada o primitiva •
Integrales elementales •
Integrales por sustitución ó
cambios de variables •
Integrales por partes •
Integrales de funciones
trigonométricas
Utilización de los métodos
Inductivo, Deductivo y
Reducción al absurdo para el
análisis y demostración de
cada una de las situaciones
presentadas en el Cálculo
Integral y Diferencial. Dialogo
didáctico real y dialogo
didáctico simulado
Prueba Escrita
20%
3era Semana
Apóstol, T. (1979). Cálculo. (3ª ed.). Barcelona: Reverté. Aires, F. (1983). Cálculo
Diferencial e Integral. (4ª ed.). México: Serie Schaum. Ayres Jr., F. y Mendelson, E. (2001).
Cálculo. (4ª ed.). Bogotá, Colombia: Mc Graw Hill. Barnett, R., Ziegler, M., Byleen, K.
(1999). Precálculo, Funciones y Gráficas. (1ª ed.). México: Mc Graw Hill. Bers, L. y Karal, F.
(1978). Cálculo. (2ª edición). México: Interamericana Ceder, J. y outcalt, D. (1971). Cálculo.
(2ª ed.). Bogotá, Colombia: Interamericana. Courant, R. y Fritzuohn. (1982). Introducción al
Cálculo y al Análisis Matemático. (4ª ed.). México: Limusa. Cruse, A. y Lehman, M. (1971).
Lecciones de Cálculo I. (1ª ed.). México: Fondo Editorial Interamericano. Dávila, A. y otros.
(1996). Introducción al Cálculo. Carácas. Mc Graw Hill. Guerra, C. (2001). Matemática 1.
(1ª ed.). Barinas, Venezuela: UNELLEZ. Granville, W. (1980). Cálculo Diferencial e Integral.
(3ª ed.). México: Limusa. Kuratowski, K. (1970). Introducción al Cálculo. (2ª ed.). México:
Limusa. Lang, S. (1976). Cálculo. (3ª ed.). México: Fondo Educativo Venezolano. Larson,
R., Hostetler, R., (1987). Cálculo y Geometría Analítica. (2ª ed.). Madrid, España: Mc Graw
Hill. Leithold, Louis. (1986). El Cálculo con Geometría Analítica. (5ª ed.). México: Harla.
Pinney, D. (1987). Cálculo y Geometría Analítica. México: Prentice Hall. Piskunov, N.
(1977). Cálculo Diferencial e Integral. (1ª ed.). URSS: MIR Proter, M. (1990). Cálculo con
Geometría Analítica. (3ª ed.). EUA: Fondo Educativo Interamericano.
II
Que el estudiante sea capaz
de entender el concepto de
integral Indefinida y aplicarlo
a la resolución de problemas
matemáticos
• Integrales de funciones
racionales • Integrales de
funciones irracionales •
Integrales trigonométricas y
por sustitución trigonométrica
Utilización de los métodos
Inductivo, Deductivo y
Reducción al absurdo para el
análisis y demostración de
cada una de las situaciones
presentadas en el Cálculo
Integral y Diferencial. Dialogo
didáctico real y dialogo
didáctico simulado
Prueba Escrita
30%
7ma semana
Ayres Jr., F. y Mendelson, E. (2001). Cálculo. (4ª ed.). Bogotá, Colombia: Mc Graw Hill.
Barnett, R., Ziegler, M., Byleen, K. (1999). Precálculo, Funciones y Gráficas. (1ª ed.).
México: Mc Graw Hill. Bers, L. y Karal, F. (1978). Cálculo. (2ª edición). México:
Interamericana Ceder, J. y outcalt, D. (1971). Cálculo. (2ª ed.). Bogotá, Colombia:
Interamericana. Courant, R. y Fritzuohn. (1982). Introducción al Cálculo y al Análisis
Matemático. (4ª ed.). México: Limusa. Cruse, A. y Lehman, M. (1971). Lecciones de
Cálculo I. (1ª ed.). México: Fondo Editorial Interamericano. Dávila, A. y otros. (1996).
Introducción al Cálculo. Carácas. Mc Graw Hill. Guerra, C. (2001). Matemática 1. (1ª ed.).
Barinas, Venezuela: UNELLEZ. Granville, W. (1980). Cálculo Diferencial e Integral. (3ª
ed.). México: Limusa. Kuratowski, K. (1970). Introducción al Cálculo. (2ª ed.). México:
Limusa. Lang, S. (1976). Cálculo. (3ª ed.). México: Fondo Educativo Venezolano. Larson,
R., Hostetler, R., (1987). Cálculo y Geometría Analítica. (2ª ed.). Madrid, España: Mc Graw
Hill. Leithold, Louis. (1986). El Cálculo con Geometría Analítica. (5ª ed.). México: Harla.
Pinney, D. (1987). Cálculo y Geometría Analítica. México: Prentice Hall. Piskunov, N.
(1977). Cálculo Diferencial e Integral. (1ª ed.). URSS: MIR Proter, M. (1990). Cálculo con
Geometría Analítica. (3ª ed.). EUA: Fondo Educativo Interamericano. Rabuffetti, H. (1993).
Introducción al Análisis Matemático. (12ª ed.). Buenos Aires: El Ateneo. Stein, Sh. (1984).
Cálculo y Geometría Analítica. (3ª ed.). México: Mc Graw Hill. Swokowski, E. (1979).
Cálculo con Geometría Analítica. E.U.A.: Wadswirth Internacional Iberoamericana. Taylor,
H., Wade A. (1979). Cálculo Diferencial e Integral. México: Limusa.
Fecha: 2-06-2016
2/2
UNELLEZ
III
Que el estudiante sea capaz
de entender el concepto de
integral definida y aplicarlo a
la resolución de problemas
matemáticos.
• La integral definida por
definición • La integral
definida como área entre
curvas • Teoremas clásicos:
Teorema de valor medio,
Teorema fundamental del
cálculo • Cálculo de áreas
ente curvas planas • Centro
de gravedad • Longitud de
arco
Utilización de los métodos
Inductivo, Deductivo y
Reducción al absurdo para el
análisis y demostración de
cada una de las situaciones
presentadas en el Cálculo
Integral y Diferencial. Dialogo
didáctico real y dialogo
didáctico simulado
Prueba Escrita
30%
10decsemana
Ayres Jr., F. y Mendelson, E. (2001). Cálculo. (4ª ed.). Bogotá, Colombia: Mc Graw Hill.
Barnett, R., Ziegler, M., Byleen, K. (1999). Precálculo, Funciones y Gráficas. (1ª ed.).
México: Mc Graw Hill. Bers, L. y Karal, F. (1978). Cálculo. (2ª edición). México:
Interamericana Ceder, J. y outcalt, D. (1971). Cálculo. (2ª ed.). Bogotá, Colombia:
Interamericana. Courant, R. y Fritzuohn. (1982). Introducción al Cálculo y al Análisis
Matemático. (4ª ed.). México: Limusa. Cruse, A. y Lehman, M. (1971). Lecciones de
Cálculo I. (1ª ed.). México: Fondo Editorial Interamericano. Dávila, A. y otros. (1996).
Introducción al Cálculo. Carácas. Mc Graw Hill. Guerra, C. (2001). Matemática 1. (1ª ed.).
Barinas, Venezuela: UNELLEZ. Granville, W. (1980). Cálculo Diferencial e Integral. (3ª
ed.). México: Limusa. Kuratowski, K. (1970). Introducción al Cálculo. (2ª ed.). México:
Limusa. Stein, Sh. (1984). Cálculo y Geometría Analítica. (3ª ed.). México: Mc Graw Hill.
Swokowski, E. (1979). Cálculo con Geometría Analítica. E.U.A.: Wadswirth Internacional
Iberoamericana. Taylor, H., Wade A. (1979). Cálculo Diferencial e Integral. México: Limusa.
Tomas, G., Finney, R. (1987). Cálculo con Geometría Analítica. (6ª ed.). México: Sistemas
Técnicos de Edición.
IV
Que el estudiante sea capaz
de entender las propiedades
y operaciones de funciones
de varias variables reales y
aplicarlos a la resolución de
problemas matemáticos.
• . Funciones reales de una y
más variables reales. •
Definición; Dominio. •
Introducción al límite de
funciones reales de dos y
tres variables reales. •
Introducción a las derivadas
parciales de primer orden de
funciones reales de dos y
más variables reales
Utilización de los métodos
Inductivo, Deductivo y
Reducción al absurdo para el
análisis y demostración de
cada una de las situaciones
presentadas en el Cálculo
Integral y Diferencial..
Prueba Escrita
20%
12decsegunada
Apóstol, T. (1979). Cálculo. (3ª ed.). Barcelona: Reverté. Aires, F. (1983). Cálculo
Diferencial e Integral. (4ª ed.). México: Serie Schaum. Ayres Jr., F. y Mendelson, E. (2001).
Cálculo. (4ª ed.). Bogotá, Colombia: Mc Graw Hill. Barnett, R., Ziegler, M., Byleen, K.
(1999). Precálculo, Funciones y Gráficas. (1ª ed.). México: Mc Graw Hill. Bers, L. y Karal, F.
(1978). Cálculo. (2ª edición). México: Interamericana Ceder, J. y outcalt, D. (1971). Cálculo.
(2ª ed.). Bogotá, Colombia: Interamericana. Courant, R. y Fritzuohn. (1982). Introducción al
Cálculo y al Análisis Matemático. (4ª ed.). México: Limusa. Cruse, A. y Lehman, M. (1971).
Lecciones de Cálculo I. (1ª ed.). México: Fondo Editorial Interamericano. Dávila, A. y otros.
(1996). Introducción al Cálculo. Carácas. Mc Graw Hill. Guerra, C. (2001). Matemática 1.
(1ª ed.). Barinas, Venezuela: UNELLEZ. Granville, W. (1980). Cálculo Diferencial e Integral.
(3ª ed.). México: Limusa. Kuratowski, K. (1970). Introducción al Cálculo. (2ª ed.). México:
Limusa. Lang, S. (1976). Cálculo. (3ª ed.). México: Fondo Educativo Venezolano. Larson,
R., Hostetler, R., (1987). Cálculo y Geometría Analítica. (2ª ed.). Madrid, España: Mc Graw
Hill. Leithold, Louis. (1986). El Cálculo con Geometría Analítica. (5ª ed.). México: Harla.
Pinney, D. (1987). Cálculo y Geometría Analítica. México: Prentice Hall. Piskunov, N.
(1977). Cálculo Diferencial e Integral. (1ª ed.). URSS: MIR Proter, M. (1990). Cálculo con
Geometría Analítica. (3ª ed.). EUA: Fondo Educativo Interamericano. Rabuffetti, H. (1993).
Introducción al Análisis Matemático. (12ª ed.). Buenos Aires: El Ateneo. Stein, Sh. (1984).
Cálculo y Geometría Analítica. (3ª ed.). México: Mc Graw Hill. Swokowski, E. (1979).
Cálculo con Geometría Analítica. E.U.A.: Wadswirth Internacional Iberoamericana. Taylor,
H., Wade A. (1979). Cálculo Diferencial e Integral. México: Limusa. Tomas, G., Finney, R.
(1987). Cálculo con Geometría Analítica. (6ª ed.). México: Sistemas Técnicos de Edición.