Se tiene una rectificadora plana de husillo porta muelas vertical y

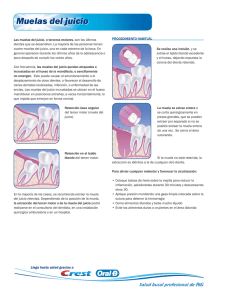
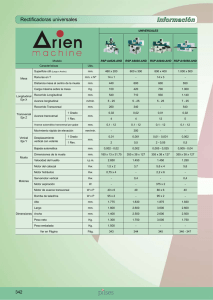
Universidad de Navarra
Nafarroako Unibertsitatea
Escuela Superior de Ingenieros
Ingeniarien Goi Mailako Eskola
ASIGNATURA GAIA: TECNOLOGÍAS DE FABRICACIÓN
Tiempo: 1 hora
3 puntos
CURSO KURTSOA: 4º
NOMBRE IZENA:
FECHA DATA: 13.09.06
P2_SEP_06
Se tiene una rectificadora plana de husillo porta muelas vertical y con mesa giratoria de 400 mm
de diámetro cuyo eje de giro es paralelo al del husillo porta muelas. La muela es de tipo vaso con
diámetro D=20 mm (ver figura) y altura T=20 mm.
En esta máquina se va a realizar un proceso de las siguientes características:
Sobre la mesa se fijan 15 piezas cúbicas de 10 mm de arista, con bastante espacio entre ellas, en
una circunferencia de 200 mm de diámetro. La muela gira a Nm=3000 rpm y la mesa a NM=10
rpm. Se pretende eliminar una capa de 0,5 mm de cada una de las 15 piezas y se selecciona una
velocidad de avance vertical de la muela equivalente a 0,01 mm por vuelta de la mesa giratoria.
Se elige un tiempo de apagado de chispa tap de 0,5 min.
Se pide:
1) a) Dibujar una vista en alzado de la máquina y marcar sobre el dibujo el eje Z positivo. b)
Calcular el top de la operación. (4 puntos)
2) a) Calcular el caudal de viruta medio ( Z W ). b) Calcular el caudal cuando la periferia de la
muela está actuando sobre la cara de una pieza, sabiendo que, debido a las deformaciones
elásticas del conjunto pieza-muela-estructura de la máquina, no se elimina más que un 80% del
avance vertical. (4 puntos)
3) a) Dibujar en perspectiva la trayectoria que un punto del eje de la muela describe con respecto
a la mesa giratoria durante una sola vuelta de dicha mesa. b) Acotar dicha trayectoria. (4 puntos)
4) a) Dibujar la marca que deja un grano de la muela sobre la superficie plana de una pieza
cualquiera y b) calcular el ángulo (η) que forma la tangente a dicha marca con la tangente a la
muela en el punto en que la trayectoria del grano considerado corta a la circunferencia de 200
mm con centro en el eje de la mesa giratoria. (4 puntos)
5) a) Deducir la expresión del volumen medio de viruta (Vv) cuando la periferia de la muela está
actuando sobre la superficie transitoria de una pieza. b) Calcular dicho valor sabiendo que δg =5
granos activos/mm2 y que, como se ha dicho en 2), no se elimina más que un 80% del avance
vertical. c) Si se dobla la velocidad de giro de la muela Nm dejando los demás parámetros del
proceso sin tocar, ¿cuál será el nuevo valor de Vv? (5 puntos)
P2_SEP_06
1.
a) Vista en alzado de la máquina (1 punto)
Z
Nm
MUELA
PIEZA
MESA
∅colocación pieza
NM
b) Tiempo de operación: t OP = t m + t ap
Velocidad de avance en z: VZ = f Z ⋅ N M = 0.01
Tiempo de mecanizado: t m =
mm
⋅ 10 rpm = 0.1 mm / min
vta pieza
0.5 mm
e
=
= 5 min
VZ 0.1 mm / min
(1 punto)
(1 punto)
t OP = 5 + 0.5 = 5.5 min
2. a) Caudal medio: Z W =
(1 punto)
mm 3
Vol. e lim . 15 ⋅ [10 mm ⋅ 10 mm ⋅ 0.5 mm]
=
= 136.36
(1 punto)
min
t OP
5.5 min
b) Z W = k ⋅ f Z ⋅ l pieza ⋅ π ⋅ D coloc.pieza ⋅ N M = 0.8 ⋅ 0.01 mm ⋅ 10 mm ⋅ π ⋅ 200 mm ⋅ 10 rpm = 502.65
mm 3
min
(1 punto)
3. Dibujo: (2 puntos)
Acotación: (2 puntos)
fz= 0.01
mm/vta mesa
∅ 200 mm
Inicio
Fin
4. a)
Marca
V=π·Dcoloc·NM
Nm
(1 punto)
Vc=π·Dm·Nm
Tangente a la
marca en ∅200
b) Del triángulo de velocidades,
tan (η) =
V π ⋅ D coloc ⋅ N M D coloc ⋅ N M
=
=
VC
Dm ⋅ Nm
π ⋅ Dm ⋅ Nm
Ángulo η
D
⋅ NM
η = arctan coloc
 Dm ⋅ Nm



Sustituyendo los valores,
V=π·Dcoloc·NM
 200 mm ⋅ 10 rpm 
 = 1.91º
η = arctan
 20 mm ⋅ 3000 rpm 
(2 puntos)
(1 punto)
5. a)




l C ⋅ k ⋅ f Z ⋅ δ g ⋅ VV
ZW

N V = lC ⋅ k ⋅ f Z ⋅ δg  ⇒ ZW =
= k ⋅ f Z ⋅ δ g ⋅ VV ⋅ VC ⇒ VV =
lC
k ⋅ f Z ⋅ δ g ⋅ VC


VC
l

∆t = C

VC
ZW =
N V ⋅ VV
∆t
b) Sabiendo que la velocidad de corte VC es igual a π·Dm·Nm
valores, se obtiene
VV =
ZW
=
k ⋅ f Z ⋅ δg ⋅ π ⋅ Dm ⋅ N m
(3 puntos)
y sustituyendo los
502.65 mm 3 / min
mm 3
= 0.066
(1 punto)
granos
grano
⋅ π ⋅ 20 mm ⋅ 3000 rpm
0.8 ⋅ 0.01 mm ⋅ 5
mm 2
c) De la ecuación anterior, se desprende que si la velocidad de giro Nm se
dobla, el volumen medio VV se reduce a la mitad.→ VV = 0.033 mm 3 / grano
(1 punto)