Conceptos básicos de optimización Problemas de

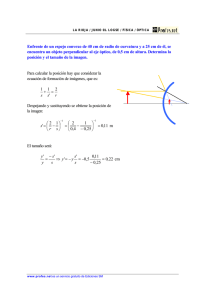
Problemas de Optimización
Conceptos básicos de
optimización
Prof. Cesar de Prada
Dpt. Ingeniería de Sistemas
y Automática
UVA
[email protected]
Para encontrar una solución al
problema es importante:
min J ( x )
x
1. Estudiar las propiedades
matemáticas de las funciones
que intervienen en el problema
hi (x) = 0
g j (x) ≤ 0
Problema general NPL
Indice
–
–
Formulación
Optimos locales y globales
Factibilidad
–
x = (x1, x2, ...., xn)’ vector de variables de
decisión
hi (x) = 0
J(x) función de costo
g j (x) ≤ 0
h(x) = 0 i = 1,2,...,l
igualdad
restricciones de
gj(x)≤ 0 j = 1,2,...,m
desigualdad
restricciones de
x ∈ Rn
Continuidad
Convexidad
Tipos de problemas de optimización
Si no existen hi ni gj el problema se denomina sin
restricciones
Equivalencias
min J ( x )
min J ( x )
x
Propiedades matemáticas
–
Un problema de optimización NLP
Conceptos Generales
–
2. Estudiar la estructura
matemática del problema, los
distintos tipos que se
presentan y las técnicas de
solución particulares para
cada uno de ellos
Contornos / Curvas de nivel
J(x)
J(x)
x = (x1, x2)’
x2
x
hi (x) = 0
Minimizar / Maximizar
min J(x) = max –J(x)
J1
g j (x) ≤ 0
gj(x) ≤ a puede escribirse como gj(x) – a ≤ 0
x*
x
x1
J(x)
gj(x) ≤ 0 es equivalente a -gj(x) ≥ 0
gj(x) ≤ 0 es equivalente a gj(x) + ε = 0, ε ≥ 0
hi(x) = 0 es equivalente a hi(x) - ε ≤ 0, ε ≥ 0
J1
x2
x*
x
J2
J3
x1
Factibilidad
Factibilidad
min J ( x )
min J ( x )
J(x)
x
x2
x
hi (x) = 0
hi (x) = 0
g j (x) ≤ 0
J1
J2
J3
F
g j (x) ≤ 0
x1
Definen la región de
busqueda o
conjunto factible F
x1
Definen la región de
busqueda o
conjunto factible F
F
Si no hay ningún punto x que satisfaga
todas las restricciones, o sea si el
conjunto factible F es vacío, el problema
es no-factible y no existe solución
x2
Ejemplos
Restricciones activas
min ( x1 − 2) 2 + 3( x 2 − 1) 2 + 1
min ( x1 − 2)2 + 3( x 2 + 1) 2 + 1
x1 + 2 x 2 ≤ 4
x1 + 2 x 2 = 4
x1 ≥ 0
x2 ≥ 0
min J ( x )
min ( x1 + 3x 22 )
x 21 + x 2 ≤ 3
hi (x) = 0
x1 ≥ 0
g j (x) ≤ 0
x1 ≥ 0
x
x2 ≥ 0
x2
F
x1
2+
x2 ≤ 3
x1
Restricción activa en x0
Una restricción gj(x) ≤ 0 es
activa en un punto x0 si se
verifica: gj(x0) = 0
J
F
F
x1
x1+ 2x2≤ 4
x1+ 2x2= 4
Regiones conexas
x2
F
x1
Región factible F conexa
x1+ 2x2= 4
Restricción inactiva en x0
Un punto x*∈F se denomina un mínimo
local del problema de optimización si
existe un entorno de x* tal que para
cualquier otro punto x ∈ F del entorno:
F
J2
J3
(A menudo se refiere
a la solución)
Punto x0 = (2, 1)’
x1
Optimo local (mínimo local)
x2
J1
x2 ≥ 0
x2
x2
J
x1 + 2 x 2 ≤ 4
J1
F
J2
J3
x1
J(x)
J(x*) ≤ J(x)
J(x)
Región factible F no conexa
x1*
Pueden existir
varios óptimos
locales
x2*
x
x*
Si se verifica
la
desigualdad
estricta el
óptimo es
propio
x
J(x)
Mínimos
impropios
x*
x
Optimo global
Ejemplo
J(x)
Un punto x* se denomina un mínimo
global del problema de optimización si
para cualquier punto x del conjunto
factible F:
Varios máximos y
mínimos locales
Optimo
global
J(x*) ≤ J(x)
x
x*
J(x)
Si no existe ningún
valor de x* ∈F tal
que J(x*) ≤ J(x) el
problema es no
acotado y no
existe mínimo
Problema no
acotado
x
Ejemplos
Continuidad
Curvas de
nivel
x2
J1
F
J(x)
x2
J2
J3
F
J1
Continua en x0
J2
Derivada no
definida
J3
x
x0
x1
x1
x0
lim J ( x ) existe
J(x0 )
Optimo local
x
Es importante para muchos
algoritmos trabajar con funciones
continuas y con derivadas
continuas
x →x 0
Mínimo sin restricciones
Optimo global
discontinua en x0
J(x)
existe
lim J ( x ) = J ( x 0 )
x →x 0
Continuidad
Continua pero
con derivada
discontinua en
x0
J(x)
x0
x
Métodos de optimización
basados en el cálculo de
derivadas pueden producir
oscilaciones y falta de
convergencia en la solución si
hay discontinuidades
Teorema
J(x)
J(x)
x
derivada discontinua debido
a la conversión en función
continua mediante
interpolación lineal de una
función originalmente
definida solo en puntos
discretos de x
Una función continua
J(x) tiene un mínimo
global en cualquier
conjunto F cerrado y
acotado
x1
F
x2
Convexidad
Conjunto Convexo
x2
J1
F
J2
J3
x1
x
hi (x) = 0
g j (x) ≤ 0
La intersección de dos
conjuntos convexos es convexa
∀x1 , x 2 ∈ F, ∀γ ∈ [0,1]
x = γx1 + (1 − γ ) x 2 ∈ F
F
Región convexa y
cerrada
F no-convexo
Función convexa
La función J(x) es convexa
en un conjunto convexo F si
no toma valores superiores a
los de una interpolación
lineal
F es convexo si y solo si:
F
Un conjunto F es convexo si
el segmento que une dos
puntos cualquiera del
mismo esta totalmente
contenido en F
F
F convexo
min J ( x )
La forma de la
región de
búsqueda es
importante
para los
algoritmos de
optimización
Función concava
J(x)
x1
J(x)
La función J(x) es cóncava
en un conjunto convexo F si
no toma valores inferiores a
los de una interpolación
lineal
x
x2
x
x1
x2
∀x1 , x 2 ∈ F, ∀γ ∈ [0,1]
∀x1 , x 2 ∈ F, ∀γ ∈ [0,1]
J ( γx1 + (1 − γ ) x 2 ) ≤ γJ ( x1 ) + (1 − γ )J ( x 2 )
J ( γx1 + (1 − γ ) x 2 ) ≥ γJ ( x1 ) + (1 − γ )J ( x 2 )
Si se cumple con < es estrictamente convexa
Si se cumple con < es estrictamente convexa
Convexidad
Ejemplos de funciones convexas
4
3
J(x)
J(x)
3.5
3.5
3
2.5
3
2.5
2.5
2
2
2
1.5
1.5
1.5
1
1
1
0.5
0.5
0.5
0
-0.5
0
-1
x1
x
x2
x1
x
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
exp(-x)
x2
0.5
1
1.5
2
2.5
3
3.5
x log(x) x > 0
3.5
30
3
Si J(x) es convexa, -J(x) es concava
0
0
-1
-0.5
0
0.5
1
1.5
2
2.5
3
σmax(x)
25
2.5
J(x)
20
2
15
1.5
10
1
Una función lineal es convexa y concava
5
0.5
0
-1
x1
x
x2
-0.5
0
0.5
1
|x|
1.5
2
2.5
3
3.5
0
0
0.5
xa
1
1.5
2
2.5
3
3.5
a ≥1, x > 0
Todas las
normas son
convexas.
La media
geométrica es
cóncava
3.5
Convexidad de funciones (una variable)
dJ ( x 0 )
1 d 2 J( x 0 )
(x − x 0 ) +
( x − x 0 ) 2 + ...
dx
2 dx 2
dJ( x 0 )
1 d 2 J(x 0 )
( x − x 0 )) =
( x − x 0 ) 2 + ...
J(x ) − (J( x 0 ) +
dx
2 dx 2
d 2 J(x 0 )
H=
dx 2
Convexidad de funciones
J(x) = J(x 0 ) +
J(x ) = J(x 0 ) +
∂J
∂x
∂J
J(x) − (J(x 0 ) +
∂x
1
∂ 2 J(x)
(x − x 0 ) + (x − x 0 ) '
(x − x 0 ) + ..
2
∂x 2 x
x0
0
1
∂ 2 J(x)
(x − x 0 )) = (x − x 0 ) '
(x − x 0 ) + ..
2
∂x 2 x
x0
0
1
∂ 2 J(x)
1
(x − x 0 ) '
(x − x 0 ) = (x − x 0 ) ' H(x − x 0 )
2
∂x 2 x
2
J(x)
0
Si H es continua y positiva
semidefinida la función J(x) es
convexa en un entorno de x0
J(x0)+J’(x0)(x-x0)
J(x0)+J’(x0)(x-x0)
La forma cuadrática z’Hz
determina si la función J(x) es
convexa en un entorno de x0
x0
x
Formas Cuadráticas / Matrices PD
Una forma cuadrática z’Hz es positiva definida (PD) si z’Hz > 0 ∀z
Para ello la matriz H debe tener todos sus autovalores > 0
x
Si la función J(x) es convexa en un conjunto F convexo,
entonces el conjunto:
{x x ∈ F, J(x) ≤ α}
Una forma cuadrática z’Hz es positiva semidefinida (PSD) si z’Hz ≥ 0 ∀z
α
Una forma cuadrática z’Hz es negativa definida (ND) si z’Hz < 0 ∀z
Para ello la matriz H debe tener todos sus autovalores < 0
x1
J(x) ≤ α
x2
Convexidad de funciones lineales
Regiones definidas por desigualdades o igualdades lineales son
convexas. Se denominan politopos.
En general, el conjunto definido por la
restricción no-lineal de igualdad f(x) = 0 es no
convexo
x2
es convexo
J
Para ello la matriz H debe tener todos sus autovalores ≥ 0
Conjunto f(x)=0
x0
Región J(x) ≤ α
Se dice también que la matriz H es PD
Una forma cuadrática z’Hz es indefinida si puede tomar valores positivos o
negativos para distintos valores de z
En ese caso la matriz H tiene autovalores positivos y negativos
H Hessiano
J(x)
Conjunto de puntos
que verifican
f(x1,x2) = 0
Igualmente, las funciones
lineales son convexas (y
concavas)
x2
x2
F
x1
x1
x1
Funciones cuadráticas
1
J(x) = a + b ' x + x 'Hx
2
∂J(x)
= b '+ x 'H
∂x
∂ 2 J(x)
=H
∂x 2
Convexidad de regiones cuadráticas
 a b   x1 
x2 ] 
 
c d x2 
J(x) = [ x1
Función (forma) cuadrática en R2
[ x1
La matriz H define el tipo
de forma cuadrática
 a b   x1 
x2 ] 
   ≤1
c d  x 2 
H es positiva semidefinida si Q(x) = x’Hx ≥ 0 ∀x ≠ 0 , autovalores ≥ 0
H es positiva definida si Q(x) = x’Hx > 0 ∀x ≠ 0
H es negativa definida si Q(x) = x’Hx < 0 ∀x ≠ 0
, autovalores < 0
La función cuadratica Q(x) es PD si H es PD, etc.
Convexidad de regiones cuadráticas
 1 0.5  x 1 
x 2 ]
  ≤ 1
0.5 1   x 2 
, autovalores > 0
H es negativa semidefinida si Q(x) = x’Hx ≤ 0 ∀x ≠ 0 , autovalores ≤ 0
Describe una región en R2
La convexidad es global
[x1
El conjunto x’Hx ≤ 1 es
convexo si la matriz H es
real simétrica positiva
semidefinida
Convexidad de regiones cuadráticas
[x1
Autovalores 1.5, 0.5 PD
0 .5   x 1 
 5
x 2 ]
  ≤ 1
0.25 − 2  x 2 
Autovalores 5.02, -2.02
Indefinida
1.5
12
1
10
8
0.5
25
0
20
1.5
6
4
-0.5
0.5
10
0
2
-1
1
-1.5
0
-1
0
5
2
1
0
0
-0.5
-1
-2
Función
1
15
2
J(x1 , x 2 ) = [ x1
-2
-2
-2
 1 0.5  x1 
x2 ] 
 
0.5 1   x 2 
-1.5
-1
-0.5
0
0.5
1
1.5
-5
2
-1
1
Curvas de [ x
1
nivel
 1 0.5  x1 
x2 ] 
  =α
 0.5 1   x 2 
Función cuadratica
PD
2
1
0
-1.5
0
-1
-1
-2
-2
-2
-2
-1.5
-1
-0.5
0
0.5
1
1.5
Función cuadratica
indefinida
Punto de silla
J ( x1 , x 2 ) = x12 + x 22 − x1x 2 + 2
 2 − 1 x1 
1
( x1 , x 2 )' 
  + 2
2
− 1 2  x 2 
 ∂ 2J 
∂ 2 J  2 − 1
eig  2  = 1, 3
=

2
∂x
− 1 2 
 ∂x 
J ( x1 , x 2 ) =
J ( x1 , x 2 ) = x12 + x 22 − 8x1x 2 + 2
 2 − 8 x1 
1
( x1 , x 2 )' 
  + 2
2
− 8 2  x 2 
 ∂ 2J 
∂ 2 J  2 − 8
eig  2  = −6,10
=

2
∂x
− 8 2 
 ∂x 
J ( x1 , x 2 ) =
20
15
10
5
0
Convexidad
Convexidad
Si J1(x) y J2(x) son funciones convexas en el conjunto convexo F,
entonces J1(x) + J2(x) también es convexa en F
-5
0
0.5
2
2.5
3
3.5
20
18
8
x 10
3.5
16
3
Si J1(x) y J2(x) son funciones convexas y acotadas superiormente en el
conjunto convexo F, entonces J(x) = max { J1(x), J2(x)} también es
convexa en F
1.5
2 x − 3sen ( x )
En el intervalo (0,π] ver la convexidad de:
15
1
2
14
12
2.5
10
10
2
8
6
1.5
5
4
1
2
0
0.5
1
1.5
2
2.5
3
3.5
0.5
Si J1(x) y J2(x) son funciones cóncavas y acotadas inferiormente en el
conjunto convexo F, entonces J(x) = min { J1(x), J2(x)} también es
cóncava en F
0
0
0.5
1
1.5
2
2.5
3
3.5
0
0
0.5
1
1.5
2
2.5
3
3.5
exp(2x 2 − 3sen(x) + 2) log(2x 2 − 3sen(x) + 2)
1500
16
1.4
14
Si J(x) es convexa en el conjunto convexo F, entonces J(Ax+b) es
convexa
0
x
hi (x) = 0
Si J es convexa y el conjunto F
es también convexo, un
mínimo local es también un
mínimo global
0.5
1
1.5
2
2.5
3
0.9
4
0.8
2
0.7
0
0
0.5
x
1
1.5
2
2.5
3
3.5
(2(x − 2)2 )
0
0.5
1
1.5
2
2.5
1
log x + 2
Para estudiar su convexidad en un punto puede
estudiarse el correspondiente Hessiano
Una funcion con hessiano continuo, definida sobre
un conjunto F convexo (con al menos un punto
interior) es convexa si, y solo si, el hessiano es una
matriz positiva semi-definida en F
Un conjunto definido por las expresiones gj(x)≤0 y
hi(x)=0 es convexo si las gj son convexas y las hi
lineales
Tipos de problemas de optimización
min J ( x )
x
x ∈ Rn
g j (x) ≤ 0
Si todas las restricciones de desigualdad son
convexas contribuirán a generar un conjunto
convexo. Las restricciones de igualdad, si no
son lineales, no serán en general convexas
con lo que el problema puede tener varios
mínimos locales.
3.5
(2(x − 2)2 + 4)
1
6
Resumen
min J ( x )
0
x
H
Optimización en un conjunto convexo
1.1
8
La caja convexa H de F es el
mínimo conjunto convexo que
contiene a F
1.2
10
Si J(x) es una función convexa en el conjunto convexo F, y si V(.) es
una función convexa (definida en el rango de J) y no decreciente,
entonces V[J(x)] es también convexa en F. O bien J(x) es concava y V
convexa y no creciente.
F
1.3
12
1000
500
Caja convexa (Convex hull)
2x + 3,

max  2

2x − 3sen(x) 
min J ( x )
x
hi (x) = 0
Optimización sin
restricciones
Optimización con
restricciones de
igualdad
Multiplicadores de
Lagrange
3
3.5
Tipos de problemas de optimización
Tipos de problemas de optimización
min J ( x )
min b' x
x
Ax ≤ c
x≥0
min x ' Hx + b' x
x
Ax ≤ c
x≥0
Programación lineal (LP)
función de coste y
restricciones lineales
x
hi (x) = 0
g j (x) ≤ 0
min J ( x, y)
Programación cuadrática (QP)
función de coste cuadrática y
restricciones lineales
x
h i ( x, y) = 0
g j ( x, y) ≤ 0
x ∈ Rn, y ∈ Z
Tipos de problemas de optimización
min J ( x, z )
Optimización dinámica
dz
= f ( z, x )
dt
g j (x) ≤ 0
Parte de las restricciones
vienen dadas por ecuaciones
diferenciales
x
ri ( z ) ≤ 0
min {J1 ( x ), J 2 ( x ), ....J s ( x )}
x
x ∈Ω
Optimización multiobjetivo
Hay varias funciones de
costo a minimizar
simultáneamente
Programación no lineal (NLP)
función de coste y / o
restricciones no-lineales
Programación mixta entera
(MINLP) algunas de las
variables son reales y otras
enteras