texto del capítulo T7 - Universidad de Zaragoza

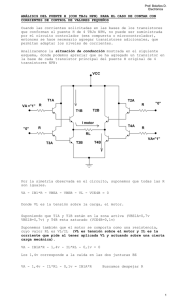
190
T7 ESTUDIO EN DETALLE DEL INVERSOR CMOS
T7.1. Inversor CMOS
T7.1. El inversor CMOS
T7.2. Tiempo de propagación y mejora del mismo
T7.3. Disipación de potencia
T7.4. Puertas CMOS
Interesa estudiar en detalle el comportamiento de las puertas CMOS y ese detalle se
refiere a tensiones, intensidades, tiempos y consumos: su función de transferencia (tensión
de salida en relación con la tensión de entrada), la intensidad suministrable por la salida,
los tiempos de conmutación, la disipación de potencia,… El inversor, como puerta más
simple, de una sola entrada, resulta sumamente adecuado para desarrollar este estudio.
En el capítulo anterior, se introdujeron los «diagramas de Memelink» como forma de
representar gráficamente la distribución de los portadores de carga en el canal de los
transistores MOS y de facilitar los cálculos relativos a tensiones e intensidades. En el caso
de un inversor, los «diagramas de Memelink» de los dos transistores que lo forman pueden
representarse conjuntamente (en un mismo diagrama), de manera tal que puede calcularse
la tensión de salida y la intensidad a través del inversor, para cualquier valor de su tensión
de entrada.
De esta forma, en el presente capítulo se calcula la tensión de conmutación del inversor
y la intensidad que consume en tal situación y se obtienen, también, las expresiones
algebraicas que corresponden a los diversos «tramos» de la función de transferencia y, a
partir de ella, los márgenes de ruido.
Asimismo es de gran interés comprender los factores que afectan a los tiempos de
propagación y cómo dichos tiempos pueden mejorarse mucho, si la carga capacitiva es alta,
utilizando una serie de inversores suplementarios, «en escalera» (cada uno de ellos de
anchura superior al anterior).
La disipación de potencia en una puerta lógica, su consumo, tiene importancia en dos
aspectos complementarios: la fuente de alimentación que ha de proporcionar suficiente
intensidad y el calentamiento del circuito que aumenta sus tiempos de propagación y, en
ocasiones, necesita adecuada refrigeración.
Por último, se recuerdan las características funcionales de las puertas CMOS y se
destaca la limitación del número de entradas de las mismas, para evitar que un alto
número de transistores en serie empeore en gran medida esas características.
Tomás Pollán Santamaría. Tecnología Electrónica. E.U.I.T.I.Z. Universidad de Zaragoza. [email protected]
Electrónica Digital
El inversor CMOS utiliza un transistor de canal N y otro de canal P:
V
CC
T
1
Vi
canal P
Vo
T
2
canal N
Supuestos V CC = 5 V y VTO,NMOS = 1 V y VTO,PMOS = -1 V
Para Vi < 1 V T1 conduce
y T2 no : Vo = VCC = V(1)
Para Vi > 4V T1 no conduce y T2 sí :
Vo = 0 V = V(0)
Las propias tensiones umbrales de los transistores aseguran las tensiones de salida
booleanas V(0) y V(1) al mantener uno de los dos transistores en corte; en ambas
situaciones booleanas, el consumo es nulo pues el transistor cortado impide el paso de
corriente a través de ambos (que se encuentran en serie).
En la figura se ha representado también la polarización de los substratos: en el diseño
físico han de configurarse las conexiones del substrato P (del transistor NMOS) a 0 V y
del substrato N (pozo) a VCC. Tales conexiones de polarización aseguran que todas las
uniones PN que forman los transistores con el substrato se encuentran polarizadas
inversamente, aislando a cada transistor respecto de su substrato.
El transistor NMOS tiene su terminal de fuente a 0 V y las tensiones de entrada VGS
y de salida VDS son positivas y su referencia es 0 V. En cambio, el transistor PMOS tiene
su terminal de fuente a VCC (se encuentra colocado «boca abajo») y las tensiones de
entrada VGS y de salida VDS son negativas, ambas con referencia a VCC.
Para analizar la función de transferencia del inversor (Vo – Vi) puede utilizarse un
diagrama de Memelink conjunto de ambos transistores. En dicho diagrama el origen de
coordenadas del transistor NMOS (punto 0,0) no coincide con el del transistor PMOS
(punto VCC,VCC) ya que la tensión de referencia, tensión de fuente, de ambos transistores
es diferente. En cambio la tensión de entrada Vi (tensión de puerta) de ambos es común y
actúa sobre el eje Y y también lo es su tensión de salida Vo (tensión de drenaje) que actúa
sobre el eje X.
En una situación estática, la intensidad que circula por ambos transistores es la
misma IT1 = IT2 (IP = IN) ya que ambos están en serie; para lo cual tiene que cumplirse
que αP.AP = αN.AN, siendo α = µ.cox.W/L el parámetro que incluye los aspectos
tecnológicos (µ.cox = Kp) y geométricos (W/L=ff) y A el efecto de las tensiones aplicadas
sobre el transistor, que viene dado (en el diagrama de Memelink) por el área limitada por
las cuatro rectas x = VS, x = VD = Vo, y = VG = Vi e y = VTO+V.
191
T7. El inversor CMOS
terminal de fuente
del PMOS: T1
VCC
T1 canal P
Vi
tensión
de puerta
de ambos
transistores
T2 canal N
192
Electrónica Digital
La tensión de entrada Vi a la cual se produce la conmutación es aquella para la cual
las áreas de los dos triángulos rectángulos e isosceles (formados por Vi con VTO + V)
cumplen la relación anterior, ya que para dicha tensión de entrada existe todo un intervalo
de tensiones de salida posibles, intervalo que corresponde al salto brusco de la
conmutación.
1
(4 − Vi )2 
β
AP

2
 AN = AP =
1
3
3
2
A N = (Vi − 1) 
2

AP =
→
VCC
0
terminal de fuente
del NMOS: T2
Vo : tensión de drenaje de ambos transistores
A N αP
µ
WP L P
=
= huecos
;
A P α N µ electrones WN L N
µ huecos
1
≈ ;
µ electrones 3
A 2 1 ff P 1
≈
= β
A1 3 ff N 3
β = (W1/L1) / (W2/L2) = ff1 / ff2 es la relación de geometrías entre ambos transistores.
Para cualquier tensión de entrada Vi la tensión de salida Vo es la que corresponde a
la siguiente relación entre áreas en el diagrama de Memelink: AN = (β/3).AP.
Tensión de conmutación
Supongamos ambos transistores iguales en dimensiones ffP/ffN = β = 1, por ejemplo,
ambos de tamaño mínimo, ¿cuál será la tensión de conmutación del inversor?:
Para tensión de alimentación 5 V y tensión umbral de ambos transistores igual a 1 V:
+5 V
La función de transferencia no es simétrica (Vi,conmutación ≠ 2,5 V) sino que la
conmutación está desplazada hacia valores inferiores de Vi, debido a la menor movilidad
de los huecos que repercute en una menor conductividad del transistor PMOS.
En la conmutación, la salida puede adoptar cualquier tensión dentro del intervalo
señalado en la figura que viene delimitado por los vértices de ambos triángulos. Teniendo
en cuenta que la recta VTO + V tiene una pendiente de 45°, los dos catetos de dichos
triángulos son iguales y su valor es respectivamente:
Vo(vértice del triángulo) = 1,1 V
NMOS: Vconmutación – VTO,NMOS = 1,1 V;
PMOS: VCC – |VTO,PMOS| - Vconmutación = 1,9 V; Vo(vértice del triángulo) = 5–1,9 = 3,1V
Es decir, la conmutación se produce con una variación vertical de la tensión de salida
entre 1,1 y 3,1 V: Vo = [1,1 – 3,1] V.
La intensidad que circula por el inversor en dicha situación de conmutación,
supuestos transistores de tamaño mínimo (ff = W/L = 1,5), será:
I = Kp.
canal P
3 (Vi − 1) = (4 − Vi ) → Vi , conmutación ≈ 2.1 V
3K p
W
1
2
(Vi,conmutación − 1)2 .
.A N = K p .1,5. (Vi − 1) =
4
L
2
Para la tecnología Ψ:
Κp (NMOS) ~ 40 µA/V2;
V
I =
120 µA
2
.(2,1 − 1) = 36 µA
4 V2
i
canal N
0
Vo
+5 V
Se aprecia en la figura que para la tensión de entrada Vi la tensión de salida Vo no es
un valor único, sino un amplio intervalo de tensiones; dicho intervalo corresponde,
precisamente, a la conmutación de la salida.
Es posible conseguir una función de transferencia simétrica, compensando, a través
de β, la relación entre las movilidades: si β = 3, resulta AP = AN y Vi = 2,5 V; para ello es
necesario hacer el transistor PMOS de anchura triple, de manera que ocupará mayor
superficie de integración y, además, aumentarán los tiempos de propagación de la puerta
anterior: los transistores PMOS dejan de ser mínimos y aumentan sus dimensiones y su
capacidad de puerta. No es, por ello, una buena solución y, en la práctica, no suele hacerse
este «equilibrado» de los transistores PMOS.
193
T7. El inversor CMOS
Habida cuenta de que la precisión del proceso de fabricación es limitada, cabe
preguntarse en qué medida una desviación en las dimensiones de los transistores afecta a
la tensión de conmutación. Supongamos que, por alguna razón, se modifican las
dimensiones de los transistores y no resultan exactamente iguales; expresando la tensión
de conmutación Vi en función de la relación de geometrías β:
(Vi − 1) = β/3 (4 − Vi ) ; Vi = 4 β/3 + 1 = 4 − 3
β/3 + 1
β/3 + 1
1
(Vi − 1)2 = β 1 (4 − Vi ) 2 ;
2
32
Si β en lugar de 1 pasa a valor 2 (modificación muy amplia, del 100 %, que equivale
a un factor de forma del transistor PMOS doble) entonces Vi = 2,35 V (desviación en la
tensión de conmutación de 0,25 V < 12 %) y, en cambio, si β pasa a 0,5 (factor de forma
del transistor NMOS doble) entonces Vi = 1,87 (desviación 0,23 V < 11 %).
194
Electrónica Digital
Para la tensión de conmutación Vconmutación = 2,1 V, las expresiones de los tramos II
y IV proporcionan, respectivamente, los valores de 3,1 V y 1,1 V entre los cuales conmuta
el inversor en dicha tensión:
Vi =Vconmutación
Vo = [3,1 ; 1,1] V
También puede obtenerse la función de transferencia mediante simulación SPICE:
las siguientes gráficas muestran, respectivamente, la función de transferencia Vo - Vi y el
consumo de intensidad de un inversor CMOS de la tecnología Ψ:
L = 1 µm, W = 1,5 µm, |VTO| = 1 V, Κp,NMOS = 40 µA/V2 y Κp,PMOS = 15 µA/V2.
5.0V
0A
4.0V
-10uA
Es decir, el efecto de una desviación en las dimensiones de los transistores sobre la
tensión de conmutación del inversor es muy pequeño.
-20uA
Función de transferencia
2.0V
El diagrama de Memelink del inversor (dos página atrás) permite obtener la curva de
transferencia (Vo - Vi) punto a punto: dado un valor de Vi, calcular el correspondiente de
Vo; puede efectuarse un análisis por tramos, obteniendo las expresiones algebraicas que
relacionan Vo con Vi en cada tramo. Los tramos diferenciados son los siguientes:
I Vi < VTO,NMOS
el transistor N no conduce y Vo = VCC
II Vi < Vconmutación
el área de conducción del transistor N es triangular
y, en cambio, el área correspondiente al P es trapezoidal
III Vi = Vconmutación
el área de conducción del transistor N es triangular
y el área correspondiente al P también es triangular
IV Vi > Vconmutación
el área de conducción del transistor N es trapezoidal
y, en cambio, el área correspondiente al P es triangular
V Vi > VCC - |VTO,PMOS|
el transistor P no conduce y Vo = 0
Supuesto un factor de forma 1 (ambos transistores iguales), con tensiones umbrales
VTO = 1 V y tensión de alimentación VCC = 5 V, la tensión de conmutación será de 2,1 V
(según los cálculos anteriores) y la de salida en los cuatro tramos antedichos se ajustará a
las siguientes expresiones:
I
Vi < 1 V
Vo = 5 V
II
1 V < Vi < 2,1 V
Vo = Vi + 1 +
III
Vi = 2,1 V
Vo = [1,1 ; 3,1]
IV
2,1 V > Vi < 4 V
Vo = Vi - 1 -
V
Vi > 4 V
Vo = 0 V
13 - 2Vi - 2Vi2
(2Vi2 + 2Vi -13) / 3
-30uA
0V
-40uA
0V
1V
2V
3V
4V
5V
V(2)
0V
1V
2V
3V
4V
5V
I(VCC)
Función de transferencia Vo – Vi CMOS
Consumo de intensidad ICC del inversor
En la función de transferencia se aprecia que, en relación con el «ruido», es
razonable extender la tensión de entrada correspondiente al 0 hasta 1,5 V (para dicho
intervalo, Vo(1) > 4,8 V) y la tensión de entrada para valor 1 puede tomarse desde 2,5 V
(intervalo para el cual Vo(0) < 0,3 V):
para Vi < 1,5 V, Vo > 4,8 V y para Vi > 2,5 V, Vo < 0,3 V.
Vo
5V
Vi
4,8 V
Márgenes de ruido en tensión:
∆V(0) = Vi,máx(0) – Vo,máx(0) = 1,5 - 0,3 = 1,2 V
2,3
2,5 V
1,5 V
1,2
0,3 V
∆V(1) = Vo,mín(1) – Vi,mín(1) = 4,8 – 2,5 = 2,3 V
Es mayor el margen correspondiente al 1 a causa del
desplazamiento de la función de transferencia hacia tensiones
bajas, debido a la menor movilidad de los huecos.
0V
Margen de ruido en potencia: ∆P = (∆V)2 / Ro. El margen de ruido en potencia (o
sea, en energía por unidad de tiempo) es más significativo que el margen en tensión, ya
que el ruido actúa como energía perturbativa sobre el circuito digital.
195
T7. El inversor CMOS
Resistencia de salida
La resistencia de salida es un parámetro indicativo del comportamiento de las puertas
lógicas (una referencia de calidad de las mismas), en cuanto a intensidad disponible en la
salida, inmunidad frente al ruido y tiempos de propagación, pues afecta fuertemente a
estos tres aspectos: en principio, cuanto menor sea la resistencia de salida mayores serán
la intensidad suministrable por la misma, el margen frente al ruido y la velocidad de
trabajo. También interesa resistencia de salida baja en relación con el acoplo en tensión,
pero dicho acoplo ya viene garantizado por el altísimo valor de la resistencia de entrada
(que es cuasi-infinita).
Las situaciones booleanas corresponden a un transistor en zona lineal: para salida 0
el transistor NMOS se encontrará conduciendo en su zona lineal, mientras que para salida
1 será el transistor PMOS el que se encuentre en zona óhmica; de forma que Ro(0) y
Ro(1) corresponden, respectivamente, a las resistencias que presentan los transistores
NMOS y PMOS en zona lineal.
196
Electrónica Digital
En todo caso, puede disminuirse el valor de la resistencia de salida aumentando en
igual medida la anchura W del correspondiente transistor, el PMOS para Ro(1) y el
NMOS para Ro(0); esto es lo que se hace, precisamente, en los adaptadores de las salidas
del circuito integrado.
La intensidad suministrable por el inversor, en cada uno de sus dos estados, depende
de la caída de tensión que admitamos en la salida: Io = ∆Vo / Ro. Esta intensidad es
relativamente pequeña y, en ocasiones, no es suficiente; por ejemplo, en los citados
adaptadores de las salidas, que precisan de una capacidad de intensidad (hacia el exterior
del circuito integrado) del orden de 10 mA. En tales casos, basta aumentar
adecuadamente el factor de forma de los transistores (ff = W / L), es decir, es necesario
hacer W >> L.
Para la tecnología Ψ:
NMOS
PMOS
Valores de las resistencias de salida (tecnología Ψ):
Ro(0) ~ 4 KΩ
Para transistores de tamaño mínimo (W=1,5L; ff=1,5) con tensión umbral de 1 V y
tensión de puerta de 5 V los valores de la resistencia equivalente en zona lineal serán:
Intensidad suministrable por el inversor: Io = ∆Vo / Ro
NMOS
Κp ≈ 40 µA/V2
PMOS
Κp ≈ 15 µA/V2
Req = 1 / (40.10-6.1,5.(5-1)) ≈ 4 kΩ
Req = 1 / (15.10-6.1,5.(5-1)) ≈ 11 kΩ
Ro(1) ~ 11 KΩ
Admitiendo ∆V(0) = 0,2 V y ∆V(1) = 0,6 V que son valores aceptables (cuya
diferencia va en relación a la asimetría de la función de transferencia y a la diferencia de
Io(0) ~ 0,2 / 4K ≈ 50 µA
Io(1) ~ 0,6 / 11K ≈ 50 µA.
márgenes de ruido):
Haciendo W > L se consiguen mayores intensidades de salida:
De manera que las resistencias de salida en situación booleana serán:
para W = 15L
Io ≈ 0,5 mA
Ro(0) ~ 4 KΩ
para W = 50L
Io ≈ 1,5 mA
para W = 300L
Io ≈ 10 mA.
Ro(1) ~ 11 KΩ
Los valores de las resistencias de salida de los inversores de tamaño mínimo son del
orden de varios KΩ, ∼103 ohmios; no son valores pequeños, pero son adecuados para el
comportamiento de las puertas booleanas en el interior del circuito integrado. Téngase en
cuenta que las capacidades de entrada de dichas puertas son pequeñas (del orden del
fentofaradio, 10-15 F) y, por ello, también lo son las intensidades que se requieren y las
constantes de tiempo que se generan (103.10-15 ∼ ps); asimismo, habida cuenta de que las
dimensiones de las conexiones son muy reducidas, el efecto del ruido es muy pequeño.
En los terminales de salida de un circuito integrado interesan resistencias de salida
inferiores a 100 ohmios (pues en este caso, se requieren intensidades del orden de 10 mA,
las capacidades de carga son del orden de 10 pF y las longitudes de las conexiones van en
centímetros); en cambio, en las puertas interiores son adecuadas resistencias del orden de
10 K (por las razones antedichas: intensidades del orden de 0,1 mA, capacidades de 1 fF y
longitud de las conexiones en micras).
Margen de ruido en potencia del inversor mínimo:
∆P (0) ~ 1,22 / 4 K ≈ 0,36 mW
∆P (1) ~ 2,32 / 11 K ≈ 0,48 mW.
El ruido actúa efectivamente como potencia: energía perturbativa por unidad de
tiempo. En los terminales de un circuito integrado se requieren márgenes de ruido
superiores de 20 mW para ambientes «normales» (viviendas o lugares públicos) y a
100 mW en ambientes «industriales»; en el interior de los circuitos integrados (en donde
la captación y efecto del ruido es muy inferior, ya que las conexiones son «milimétricas»),
son suficientes márgenes del orden de 0,1 mW.
197
T7. El inversor CMOS
198
Electrónica Digital
I
T7.2. Tiempo de propagación y mejora del mismo
V(t) = 1 + 4
T7.2.1. Tiempo de conmutación de una puerta CMOS
La salida de una puerta booleana se encontrará conectada a la entrada de otra u otras
puertas (u otros componentes del circuito global), cuyo efecto equivalente es el de una
capacidad que ha de cargarse y descargarse en la conmutación, originando unos tiempos
de retraso hasta que el proceso de carga o descarga alcanza los valores de tensión
apropiados para el 0 y 1 booleanos.
+5 V
= 1 + 4 tgh
+1
I
t
4C
La función tangente hiperbólica tgh(x) es fuertemente creciente (del tipo 1 - e-x, con
pendiente aún mayor), de forma que tiende a 1 asintóticamente y alcanza el valor 0.76
(>75 %) para x = 1.
La conmutación de la salida hacia 5 V alcanzará 4 V en un tiempo aproximado al
que corresponde a x = 1:
La determinación del tiempo de descarga a través del transistor NMOS, hasta
disminuir a 1 V, es análoga y conduce a la misma expresión t↓ = t1 + t2 = 5C / I:
VG = 0
Vo
t↑ = 5C / I(P)
Vo -1
A = Acanal saturado - 1/2 (Vo -1)2
Proceso de carga a través de un transmisor PMOS
Estudiemos el proceso de carga, expresando los tiempos de retraso en función de su
intensidad con canal saturado ISAT = I y de la capacidad de carga CL = C que soporta:
-
I = ISAT = α . Acanal saturado, siendo A el área del triángulo de conducción en el
diagrama de Memelink;
-
supuestos VCC = 5 V y VTO = 1 V: I = α .42 / 2;
α=I/8
En el proceso de carga, existen dos tiempos diferenciados:
t1: Vo de 0 a 1 V canal saturado
I1 = I, ∆Q = I. t = C.∆V, t = C.∆V/I,
t1 = C/I.
t2: Vo de 1 a 5 V canal no saturado I2 < I y decrece al aumentar Vo, I(t) dt = C dV:
I(t) = I - α . (V -
e
I
t
2C
t2 = 4C / I
t↑ = t1 + t2 = 5C / I
(I / 4C) t2 = 1
donde I es la intensidad de canal saturado del transistor PMOS.
Vo
1)2
t
e 2C − 1
/ 2 = I - (I/16) (V -
(I / 16) (16 - (V - 1)2) dt = C dV ;
1)2
= (I/16)(16 - (V -
I
d(V − 1)
dt = 2
16C
4 − (V − 1) 2
Integrando ambos miembros de la ecuación diferencial anterior:
1
4 + (V − 1)
I
ln
;
t=
2 . 4 4 − (V − 1)
16C
1)2)
I
t
4 + (V − 1)
= e 2C
4 − (V − 1)
Para la tecnología Ψ:
y para VCC = 5 V y VTO = 1 V:
t↓ = 5C / I(N)
Lmín = 1 µm, W = 1,5 µm, Ci ~ 2 fF
I(P) = Isat (canal P) ≈ 0,2 mA
I(N) = Isat (canal N) ≈ 0,5 mA
para fan-out = 1 (una sola entrada conectada a la salida de un inversor mínimo):
t↑ ≈ 10 fF / 0,2 mA ~ 0,05 ns
t↓ ≈ 10 fF / 0,5 mA ~ 0,02 ns
El tiempo de subida es superior al de bajada como consecuencia de la menor
movilidad de los huecos que conforman el canal del transistor PMOS; ello podría evitarse
dimensionando adecuadamente dicho transistor pero implicaría mayor área de integración
y, a la vez, mayor capacidad de carga de cada entrada lo cual redundaría en empeorar los
tiempos de conmutación de la puerta anterior. Por ello, no interesa dimensionar las
puertas lógicas para conseguir su simetría funcional.
Nos encontramos con tiempos de conmutación inferiores a un nanosegundo, que
dependen linealmente de la capacidad de carga y, por ello, del fan-out y de las
dimensiones de los transistores:
- al aumentar el fan-out, los tiempos de conmutación crecen en la misma proporción
- al disminuir las dimensiones de la tecnología los tiempos de conmutación se reducen
cuadráticamente (Ci disminuye con L y con W).
Para una tecnología de 0,5 micras:
Lmín = 0,5 µm, W = 0,75 µm, Ci ~ 0,5 fF
para fan-out = 1 (una sola entrada conectada a la salida de un inversor mínimo):
t↑ ≈ 2,5 fF / 0,2 mA ~ 0,015 ns
t↓ ≈ 2,5 fF / 0,5 mA ~ 0,005 ns
199
T7. El inversor CMOS
La siguiente gráfica muestra la conmutación de un inversor con un fan-out de 1, es
decir, a su salida se encuentra conectado otro inversor análogo; la simulación SPICE se ha
efectuado con los datos de la tecnología Ψ y transistores de tamaño mínimo:
L = 1 µm, W = 1,5 µm, |VTO| = 1 V, Κp,NMOS = 40 µA/V2 y Κp,PMOS = 15 µA/V2.
200
Electrónica Digital
Para facilitar la suma de tiempos, cada tiempo de propagación suele medirse por el
retraso entre el punto medio de la conmutación (tensión Vcc/2) de la onda de entrada y el
punto medio de la conmutación de la señal de salida.
Vi
5.0V
Vo
4.0V
3.0V
t pHL
2.0V
1.0V
0V
0s
50ps
100ps
150ps
200ps
250ps
300ps
350ps
400ps
450ps
500ps
V(2)
Time
Onda de conmutación de un inversor: V(2) = Vo
Los tiempos medidos en esta gráfica son: t↑ ≈ 0,071 ns y t↓ ≈ 0,026 ns .
Los tiempos de conmutación dependen también fuertemente de la temperatura, ya
que al aumentar ésta disminuye fuertemente la movilidad de los portadores (aumentan sus
choques con los núcleos de la red cristalina) y, en consecuencia, se reduce Kp y la
intensidad de saturación de los transistores. De ahí, el alto interés de evitar el
calentamiento de los circuitos integrados, disipando adecuadamente el calor generado por
la potencia consumida en ellos, si se desea aprovechar la velocidad máxima de trabajo.
El retardo que introduce un inversor es algo superior al tiempo de conmutación
calculado en este apartado: dicho tiempo de conmutación ha sido determinado en relación
con la capacidad de carga CL (fan-out) y, en la práctica, influyen también otros efectos
capacitivos internos del propio inversor.
Al conectar varios inversores seguidos, el tiempo de propagación del conjunto es
mayor que los tiempos de conmutación individuales pero es inferior a la suma de ellos, ya
que existe solapamiento entre ellos. Es decir, los tiempos de conmutación no son
linealmente acumulativos ya que cada puerta inicia su conmutación antes de que la
anterior complete la suya.
t pLH
Sin ser exactos, las formulas y cálculos anteriores ofrecen una buena estimación del
orden de magnitud y una buena aproximación al valor real de los tiempos de
propagación. La simulación SPICE de los mismos puede proporcionar aún mayor
precisión.
Además, habrá que tener en cuenta que cada conexión entre la salida de una puerta y
la entrada de la siguiente introduce una línea conductora con sendos efectos resistivo y
capacitivo y, con ello, un nuevo sumando al retardo de propagación de las señales; en
tecnologías submicrónicas no es extraño que el retardo introducido por las líneas de
conexión sea superior al tiempo de propagación de la propia puerta booleana.
T7.2.2. Mejora de los tiempos de propagación
En ocasiones las capacidades de carga son altas; por ejemplo, en los adaptadores de
las salidas de los circuitos integrados (que han de ser capaces de soportar su conexión a
cargas equivalentes de decenas de picofaradios) o, también, en puertas que deban soportar
a su salida un fan-out alto (por ejemplo, las que transmiten a los diversos biestables la
señal de reloj) o largas longitudes de polisilicio. En tales casos, los tiempos de
conmutación se elevan en demasía y es preciso reducirlos mediante adaptadores de
intensidad:
Para la tecnología Ψ:
Para una capacidad de carga de 10 pF (5.000 veces superior a Ci -fan-out 1-):
t↑ = 5C / I(P) ≈ 50 pF / 0,2 mA ≈ 0,3 µs
t↓ = 5C / I(N) ≈ 50 pF / 0,5 mA ≈ 0,1 µs
tiempos que resultan relativamente altos y limitan la velocidad a unos pocos MHz.
Para disminuir los tiempos de propagación causados por altas capacidades de carga
o, lo que es lo mismo, por la necesidad de intensidades de salida altas, se utilizan
esquemas de amplificación en cascada con inversores cuya anchura de transistor es
progresivamente creciente.
201
T7. El inversor CMOS
Ejemplo desarrollado con la tecnología Ψ:
Supongamos una carga de 2 pF que resulta ser unas 1.000 mayor que Ci (capacidad
de carga que corresponde a fan-out 1):
t↑ = 5C / I(P) ≈ 10 pF / 0,2 mA ≈ 50 ns
t↓ = 5C / I(N) ≈ 10 pF / 0,5 mA ≈ 20 ns
Añadiendo un par de inversores cuya anchura de transistores sea, en cada uno de
ellos, 10 veces la del anterior:
inversor
"mínimo"
Isat = I
Ci = 2 fF
inversor
con transistores
10 veces
más anchos
Isat = 10 I
Ci = 20 fF
inversor
con transistores
100 veces
más anchos
Isat = 100 I
Ci = 200 fF
2 pF
CL = 2000 fF
Como puede apreciarse en la figura, en cada inversor se produce un «salto» entre su
capacidad de carga y su capacidad de entrada de 10; en total, un salto de 1000 que es la
relación existente entre los 2 pF y Ci (capacidad de entrada del inversor mínimo).
t1↑ = 5 x 20 / 0,2 ≈ 0,5 ns
t2↑ = 5 x 200 / 2 ≈ 0,5 ns
t1↓ ≈ 5 x 20 / 0,5 ≈ 0,2 ns t2↓ ≈ 5 x 200 / 5 ≈ 0,2 ns
t↑ ∼ t1↑ + t2↓ + t3↑ ≈ 1,2 ns
t3↑ = 5 x 2000 / 200 ≈ 0,5 ns
t3↓ ≈ 5 x 2000 / 500 ≈ 0,2 ns
t↓ ∼ t1↓ + t2↑ + t3↓ ≈ 0,9 ns
Ambos tiempos son muy inferiores a los que presenta el primer inversor en solitario:
50 ns y 20 ns, respectivamente.
Este esquema (en que se incluyen parejas de inversores «en escalera», es decir, con
anchura de transistores creciente) resulta sumamente útil para configurar adaptadores de
intensidad (buffers), tanto para los terminales de salida del circuito integrado como para
aquellas conexiones internas que han de soportar un alto fan-out o alta carga capacitiva y,
por tanto, han de proporcionar alta intensidad.
202
Electrónica Digital
Un adaptador de intensidad puede incluir más de una pareja de inversores «en
escalera» (siempre un número par para que no se produzca una inversión suplementaria),
de forma que la relación de intensidad entre el último de ellos y la puerta «mínima» inicial
se distribuya en múltiples «saltos» pequeños.
•••
puerta previa
de tamaño
"mínimo"
Isat = I1
Ci
Isat = I L
n inversores
siendo n un nº par
CL
Se puede calcular el número óptimo de inversores para conseguir el menor tiempo de
propagación global:
- sea K el cociente entre la capacidad de carga que debe soportar el conjunto y la
correspondiente a una entrada mínima (primera puerta del conjunto): K = CL / Ci
- si el necesario aumento del fan-out se distribuye de forma homogénea siendo ∂ el
coeficiente incremental Ci+1 = ∂.Ci, será necesario que las anchuras W de transistores
de dos inversores sucesivos se incrementen en dicho factor ∂: Wi+1 = ∂.Wi
- la relación de anchuras repercute en proporción directa en la relación entre
capacidades de entrada Ci y entre intensidades de saturación Isat; se verificará que
Wi+1 / Wi = Ci+1 / Ci = Isat,i+1 / Isat,i = ∂
- el factor incremental global K corresponde a n+1 incrementos ∂ sucesivos:
K = CL / Cin = ∂ n+1, ∂ = n+1 K y el incremento en intensidad será: IL / I1 = ∂n
Los tiempos de propagación de los inversores serán iguales, ya que la relación entre
intensidad de saturación y capacidad de carga es constante, y dichos tiempos serán
proporcionales a ∂ ya que dicho factor representa la carga relativa a su tamaño que cada
inversor soporta. Por tanto, el tiempo de propagación del conjunto será proporcional a
(n+1).∂ y la situación de tiempo mínimo de propagación corresponde a:
d[(n + 1).∂ ]
= 0;
dn
∂ = n +1 K
d((n + 1) n +1 K )
=0;
dn
1 − lnK.
n +1

1 
K + (n + 1).n +1 K .lnK.−
=0
(n
+
1) 2 

1
= 0 ; n + 1 = lnK ; K = e n +1 ;
(n + 1)
∂ = n +1 K = e = 2,7
203
T7. El inversor CMOS
La adaptación óptima de la «escalera de inversores», para conseguir tiempos
mínimos de propagación, se consigue cuando el número de inversores es n + 1 = lnK y,
en este caso, el coeficiente incremental ∂ coincide con el número e:
Wi+1 = 2,7.Wi
Ci+1 = 2,7.Ci
Isat,i+1 = 2,7. Isat,i
El tiempo de propagación de cada inversor será ∂ = e = 2,7 veces el correspondiente
a un inversor mínimo conectado a otro inversor análogo.
En el ejemplo desarrollado con la tecnología Ψ:
CL = 2 pF; Cin = 2 fF: K = 1000; n+1 = ln(1000) ≈ 7
El mínimo tiempo de propagación se obtiene con 6 inversores intermedios, cuya
anchura de transistores sea, en cada uno de ellos, 2,7 veces mayor que en el anterior.
Los tiempos de propagación de cada uno de los inversores son los siguientes:
ns
t↑ = 2,7 x 5 x 2 fF / 0,2 mA ≈ 0,15 ns
t↓ = 2,7 x 5 x 2 pF / 0,5 mA ≈ 0,05
De forma que, los tiempos de propagación para el conjunto total serán:
t↑ ∼ 4t↑ + 3t↓ ≈ 0,8 ns
t↓ < 4t↓ + 3t↑ ≈ 0,7ns.
Tales son los tiempos mínimos de propagación que pueden conseguirse, claramente
inferiores a los que presentaría el primer inversor actuando en solitario sobre la capacidad
de carga 2 pF (60 ns y 20 ns, respectivamente) y solamente un poco inferiores a los que
se obtienen con una sola pareja de inversores en escalera (1,5 ns y 1 ns).
Como puede apreciarse añadir una primera pareja de inversores (adecuadamente
dimensionados) tiene un gran efecto tiene respecto a la reducción de tiempos; cuando se
añaden más parejas de inversores (ajustando en cada caso su anchura W), la inclusión de
cada una de ellas tiene un efecto sucesivamente menor que la anterior. Por ello, debe
valorarse la reducción de tiempos que se desea conseguir en relación con el área de silicio
que se va a necesitar.
204
Electrónica Digital
T7.3. Disipación de potencia
La potencia disipada por un inversor CMOS en situación estática es prácticamente
nula, pues no existe ninguna línea de conducción directa entre alimentaciones (siempre
uno de los dos transistores correspondientes a cada entrada se encuentra en corte). Ahora
bien, en cada transistor existen uniones PN polarizadas inversamente (uniones difusiónsubstrato) que conducen una minúscula intensidad inversa, cuyo orden de magnitud es del
picoamperio (mA / 106).
Ahora bien, al conmutar el inversor han de cargarse o descargarse las capacidades
propias de sus transistores, en particular, su capacidad de puerta, lo cual determina un
consumo dinámico proporcional a la frecuencia de conmutación:
- energía necesaria para cargar o descargar un condensador: 1/2 C.V2
- potencia disipada al cargarlo y descargarlo con una onda de frecuencia f
(en cada período hay dos conmutaciones, habrá que contabilizar una carga y una
descarga): (1/2 C.V2) . 2f = C . V2 . f
Esta potencia (energía por unidad de tiempo) representa un consumo de intensidad
desde la alimentación y una disipación de calor en el propio circuito. Son dos aspectos
complementarios, relativos al consumo de intensidad, que requieren la correspondiente
atención en el diseño y utilización del circuito integrado: una fuente de alimentación con
suficiente capacidad de suministro de corriente y una disipación de calor adecuada.
Teniendo en cuenta, además, que los tiempos de propagación aumentan con la
temperatura y, en consecuencia, disminuye la velocidad de trabajo.
Conforme a la anterior expresión, la potencia consumida y disipada depende de:
-
la tecnología, cuyas dimensiones determinan la capacidad C; dicha capacidad
equivalente de una puerta a efectos de consumo de intensidad tiene varios
componentes, entre los cuales predomina la capacidad de entrada (las otras
capacidades internas de los transistores son de valores muy inferiores) que es
proporcional a la superficie de las zonas de puerta, es decir, al producto L.W y
disminuye cuadráticamente al disminuir L (W = 1,5L);
-
la tensión de alimentación, que también afecta cuadráticamente V2; existe, por
ello, una evolución continuada de la microelectrónica hacia tensiones de
alimentación más bajas (el paso de 5 V a 3 V reduce el consumo a la tercera
parte), siendo cada vez más frecuentes dispositivos de 2,5 V y de 1,8 V;
la frecuencia de trabajo f, aumentando linealmente con ella (lo cual aconseja no
trabajar a frecuencia más alta de la estrictamente necesaria para el sistema digital)
-
Al evaluar el consumo de un circuito integrado, debe tenerse en cuenta que no todas
las puertas del mismo conmutan cada vez, sino que solamente lo hace una pequeña parte
de ellas; por ejemplo, la escritura de un dato sobre una memoria de 1 Mega solamente
afecta a uno de sus 1048576 registros (y al decodificador de direcciones y control de
escritura).
205
T7. El inversor CMOS
Disipación de potencia (tecnología Ψ):
Para transistores de tamaño mínimo (L = 1 µm, W =1,5 µm) y espesor de óxido de
puerta tox de 50 nm, el valor de la capacidad de puerta será:
Cox = 0.7 fF / µm2;
206
El orden de magnitud del «pico de intensidad» en la conmutación fue calculado en el
apartado anterior, por medio del área de conducción en el diagrama de Memelink; en
situación de conmutación (Vi = 2,1 V), la intensidad que circula por el inversor,
supuestos transistores de tamaño mínimo (ff = W/L = 1,5), será:
CG = Cox . W . L = 0,7 fF / µm2 . 1,5 µm . 1 µm ≈ 1 fF.
Como la entrada del inversor se encuentra conectada a dos transistores, uno de canal
N y otro de canal P, la capacidad de entrada será: Ci ≈ 2 fF
Para la tensión de alimentación habitual de 5 V (VCC = 5 V)
P = C.V2. f = 2 fF . 25 V2 . f = 50 . 10-15 . f = 0,05 . f pW
Para f = 1 MHz = 106:
P = 50 nW / MHz;
ICC = 10 nA / MHz
Al aumentar la frecuencia aumenta la potencia disipada en cada entrada en igual
proporción.
Es posible hacer una estimación de la potencia disipada en 1 mm2 ocupado por
puertas CMOS, supuesto que todos los transistores conmuten (lo cual no es una situación
normal pues en cualquier bloque digital sólo conmuta una pequeña fracción de las puertas
contenidas en él). El área activa ocupada por los transistores en cuanto a su zona de
puerta (L.W) suele ser inferior al 5 % (ya que la mayor parte de la superficie es necesaria
para las zonas de fuente y drenaje, conexiones, separaciones,...):
1 mm2 = 1000000 µm2; 5 % ( 1 mm2 ) = 50000 µm2
Ctransistores = Cox . superficie activa = 0,7 . 50000 = 35 pF
P = C . V2. f = 875 pW. f ~ 1 nW . f
Para f = 1 MHz, P ~ 1 mW / MHz, es decir, supuesto que todos los transistores
contenidos en 1 mm2 de silicio conmutasen, dicho milímetro cuadrado de silicio debería
disipar en forma de calor una potencia del orden de 1 mW/MHz; esta potencia no depende
de las dimensiones de la tecnología sino del porcentaje de ocupación: superficie
activa/superficie total (entendiendo por superficie activa la ocupada por las puertas de los
transistores).
Además de la disipación de potencia de tipo capacitivo (principalmente la capacidad
de entrada de los transistores MOS) existe otro efecto dinámico debido a que en la
conmutación, durante un breve instante de tiempo, conducen ambos transistores PMOS y
NMOS, dando lugar a un estrecho «pico de intensidad»; tal efecto resulta despreciable
frente al anterior siempre que la conmutación sea adecuadamente rápida (tiempos de
conmutación inferiores a 1 ns).
Sin embargo, dichos «picos de intensidad» deben ser tenidos en cuenta en relación
con el «ruido», ya que al ser variaciones muy rápidas de intensidad generarán «picos de
tensión» sobre las líneas de alimentación (por efecto inductivo).
Electrónica Digital
I =
Para la tecnología Ψ:
3K p
4
(Vi − 1)2 .
I =
340 µA
2
.(2,1 − 1) = 36 µA
4 V2
P = 180 µW
Un inversor, cuya entrada se encuentre en situación de alta independencia
(tri-estado) o con un valor de tensión intermedio (~Vconmutación) genera una disipación de
potencia del orden de 0,2 mW y el correspondiente calentamiento del circuito (un valor
unas cuatro mil veces superior al generado en la conmutación de dicho inversor a 1MHz).
Por otra parte, existe una situación peligrosa en que este pico de intensidad (debido a
la conducción «momentánea» de ambos transistores en la conmutación) puede ser estable
y originar un fuerte calentamiento (e incluso la destrucción) del circuito integrado: si una
entrada queda en alta impedancia tiende a adoptar un valor de tensión intermedia y
ambos transistores conducen.
Esta situación puede darse en caso de utilizar buses (o adaptadores tri-estado)
internos que puedan quedar en alta impedancia, posibilidad que puede evitarse
conectando en cada línea una resistencia de alto valor, que la referencie a 0 V (pulldown), o bien un pequeño biestable (un par de inversores) que mantenga el último valor
booleano establecido en ella (ver figura).
línea tri-estado
biestable
que conserva
el último valor recibido
Conjuntos de circuitos auxiliares de este tipo, cuya finalidad es que las líneas de
buses no se queden en estado de alta impedancia, se encuentran también disponibles en
los catálogos de circuitos integrados.
207
T7. El inversor CMOS
T7.4. Puertas CMOS
VCC
m
...
las entradas se activan con valor 0:
paralelo <> operación "y"
serie
<> operación "o"
+ una inversión global
Plano
P
y
a
b
c
m
...
Plano
N
las entradas se activan con valor 1:
serie
<> operación "y"
paralelo <> operación "o"
+ una inversión global
porque transmiten el valor 0
Vc c
a
c
b
d
e
y = (a +b) .c + d.e
d
c
a
Electrónica Digital
Características físicas de las puertas complementarias
Haciendo uso del álgebra de conmutadores, las puertas lógicas CMOS se construyen
mediante dos planos «duales» de transistores: plano N y plano P; a cada entrada le
corresponden sendos transistores, uno en el plano N y otro en el plano P, conectados de
acuerdo con la dualidad serie-paralelo.
a
b
c
208
b
e
- en su plano N, la configuración de transistores corresponde (de acuerdo con el álgebra
de conmutadores) a la función (a + b).c + d.e , a la cual debe añadirse una negación
global ya que dicho plano N transmite el valor 0; de forma que la función conformada
por el plano N de la figura anterior es: y = (a + b).c + d.e
- en cuanto al plano P, transmite el valor 1 pero sus transistores conducen cuando su
entrada es 0, es decir, corresponden a variables negadas ( a, b, c, d, e ) y su
configuración (de acuerdo con el álgebra de conmutadores) conforma la función
(a . b + c) . (d + e) ; de manera que la función conformada por el plano P de la
figura es la misma que la del plano N: y = (a . b + c) . (d + e) = (a + b).c + d.e
Permiten una amplia diversidad de puertas
El juego de conexiones serie-paralelo permite configurar funciones complejas y muy
diversas en una misma puerta, con la limitación de que la expresión algebraica de la
función ha de presentar una negación global sobre el conjunto de operaciones booleanas
(son puertas inversoras) y de que tal negación sea la única que aparezca: cada negación
da lugar a una puerta adicional.
Los transistores P y N presentan diferente resistividad (debida a la menor movilidad
de los huecos): la conexión PMOS en paralelo, y sus correspondientes NMOS en serie,
contribuye a compensar la asimetría, mientras que la conexión de PMOS en serie acentúa
dicha asimetría y su efecto resistivo; por ello, son preferibles las puertas "y-negada"
(Nand) a las puertas "o-negada" (Nor).
Las entradas son de tipo capacitivo
Los transistores presentan una capacidad de puerta, que es preciso cargar o descargar
en la conmutación cuando cambia el valor booleano presente en la correspondiente
entrada; tal transitorio de carga o descarga:
- da lugar a unos tiempos de conmutación que limitan su velocidad de trabajo;
- limita, asimismo, el fan-out de la puerta anterior, es decir, el número de entradas de
otras puertas que pueden conectarse sobre una salida (pues tal número condiciona la
velocidad de trabajo);
- requiere un aporte puntual de intensidad durante la conmutación, que da lugar a un
consumo dinámico proporcional a la frecuencia de conmutaciones;
- genera «ruido» sobre las líneas de alimentación como consecuencia del «pulso» de
intensidad necesario para la conmutación.
La salida de cada puerta es resistiva
Cada plano de transistores, cuando conduce, presenta una resistencia relativa a la
zona lineal u óhmica de sus transistores; tal resistencia depende de las dimensiones de los
transistores (disminuyendo en proporción inversa a la anchura de estos) y afecta a:
- la intensidad suministrable por la puerta;
- los procesos de conmutación (carga y descarga de las capacidades de entrada de las
puertas siguientes) y, en consecuencia, los tiempos de propagación y la velocidad;
- la inmunidad frente al «ruido» en términos de potencia.
T7. El inversor CMOS
209
210
Se presentan varios transistores en serie
La presencia de transistores en serie supone un aumento de la resistencia de salida de
la puerta, que repercute, en concordancia con el apartado anterior, en la intensidad
suministrable por la puerta, en los tiempos de propagación y la velocidad de trabajo y en
la inmunidad frente al «ruido» en términos de potencia.
En cuanto a intensidades en la salida de puertas con más de una entrada, ha de
tenerse en cuenta aquella situación booleana en que conducen varios transistores en serie,
en cuyo caso la intensidad suministrable ha de dividirse, al menos, por el número de ellos
(ya que se suman sus resistencias equivalentes) o alternativamente ha de aumentarse en
igual proporción la anchura de tales transistores.
También el margen de ruido en potencia disminuye por la suma de resistencias de
transistores en serie: ∆P = (∆V)2 / Ro.
En los tres aspectos considerados (intensidad suministrable, tiempos de propagación
e inmunidad en potencia) interviene la resistencia de salida: Ro = Σ Ro (transistores en
serie). En una primera aproximación, para n transistores se multiplica por n la resistencia
de salida correspondiente a uno sólo de ellos; pero, además, se produce un efecto de
«desplazamiento de la tensión de fuente» que aumenta progresivamente la resistencia de
los diversos transistores.
Consideremos el caso de transistores NMOS en serie, todos ellos con tensión de
entrada VG = V(1), solamente el inferior de ellos tiene su fuente conectada a 0 V y su
tensión VGS = V(1). Mientras que la tensión de salida sea Vo > 0 (lo cual ocurre siempre
que Io ≠ 0 y, en particular, durante la conmutación), la tensión puerta-fuente de los demás
transistores es menor VGS < V(1) pues su terminal de fuente no está conectado a 0 V
directamente, sino a través de los transistores que se encuentran debajo; por ello, dicha
tensión VGS disminuye al ascender en la serie y la resistencia efectiva que presenta cada
transistor es mayor cuanto más alejado se encuentra de la conexión a 0 V.
Por ello, puertas con muchas entradas (muchos transistores en serie) presentan malas
características funcionales: es altamente aconsejable limitar el número de entradas de las
puertas CMOS, de forma que no aparezcan más de 6 transistores en serie.
El consumo estático es siempre nulo
Para cada valor booleano en una de las entradas, uno de sus transistores se encontrará
en corte y el otro conducirá: todo camino de conducción entre los dos terminales de
alimentación (VCC y 0 V) incluye siempre un transistor en corte, por lo cual el consumo
en reposo es nulo.
En cambio, sí que hay consumo dinámico originado por la carga o descaga de las
diversas capacidades propias de los transistores en la conmutación y dicho consumo es
proporcional a la frecuencia de conmutación.
Electrónica Digital
Tiempos de conmutación
Al pasar de un inversor a una puerta booleana de dos o más entradas, los tiempos de
propagación aumentan en aquellos procesos (carga o descarga) en que la conducción se
produce a través de varios transistores en serie; es un efecto de suma de sus resistencias
(se suma la longitud de sus transistores).
Para la tecnología Ψ:
• NAND de 2 entradas:
t↑ = 5C / I(P) ≈ 10 fF / 0,2 mA ≈ 0,05 ns,
t↓ = 2 x 5C / I(N) ≈ 2 x 10 fF / 0,5 mA ≈ 0,04
2 transistores en serie
• NOR de 2 entradas:
t↑ = 2 x 5C / I(P) ≈ 2 x 10 fF / 0,2 mA ≈ 0,1 ns,
2 transistores en serie
t↓ = 5C / I(N) ≈ 10 fF / 0,5 mA ≈ 0,02 ns
ns
Debido a la diferente resistividad de los transistores PMOS y NMOS, interesa más la
utilización de puertas "y-negada" (Nand) pues en ellas se equilibran un poco los dos
tiempos de conmutación (aumenta el menor de ambos), mientras que para las puertas
"o-negada" (Nor) se aumenta aún más el tiempo de subida (que es, ya de por sí, el
mayor).
Ahora bien, cuando se desea obtener estimaciones cuantitativas de los tiempos de
propagación de una puerta o de un conjunto de puertas booleanas es necesario acudir a la
simulación eléctrica (SPICE u otros). Por un lado, los efectos relativos a transistores en
serie (comentados en la página anterior) y, de otro, el solapamiento entre los tiempos de
conmutación de puertas sucesivas (ya que cada puerta inicia su conmutación antes de
haber finalizado la conmutación de la puerta anterior) limita, en gran medida, los
resultados obtenidos a través de modelos simplificados o de razonamientos cualitativos.