DINÁMICA DE FLUIDOS Propiedades de los Fluidos. Concepto de

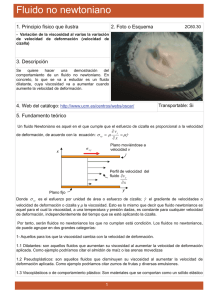
DINÁMICA DE FLUIDOS
Propiedades de los Fluidos.
Concepto de fluido. Fluido ideal.
Viscosidad
Tensión superficial. Capilaridad
Estática. Presión en un punto.
Ecuación general de la estática.
Teoremas de Pascal y Arquímedes.
Cinemática de fluidos.
Descripciones Euleriana y Lagrangiana.
Definiciones cinemáticas.
Deformación de un fluido.
Divergencia, cizalla y rotación.
Vorticidad y teorema de Stokes.
Función de corriente.
Leyes de conservación
Ecuación de continuidad.
Fuerzas en fluidos. Tensión en un punto.
Conservación de momento.
Ecuación constitutiva para fluidos newtonianos.
Ecuación de Navier-Stokes.
Soluciones particulares de la Ec. N-S.
Ecuación de energía. Ecuación de Bernouilli.
Aplicaciones.
Flujo Potencial.
Potencial de velocidades.
Función de corriente.
Ejemplos.
Semejanza dinámica.
Flujo laminar y turbulento.
Número de Reynolds.
Idea de capa límite.
Leyes de semejanza.
Concepto de Fluido:
Se conoce como fluido a todo cuerpo que carece de elasticidad de forma. Es decir no tiene una forma propia y se puede
adaptar al recipiente que lo contiene.
No presenta fuerzas internas tangenciales o éstas son muy pequeñas. Los movimientos relativos entre partículas fluidas no
realizan trabajo.
Fluidos ideales:
a) no responden a tensiones tangenciales.
b) Son continuos.
La propiedad a) implica que sólo existen
fuerzas normales entre dos parcelas de
fluido.
La hipótesis de continuidad del fluido permite hablar de densidad como función de punto.
ρ
Incertidumbre
microscópica
Incertidumbre
macroscópica
ρ0
δv*
δv
δv
ρ0
ρ=
lim
δv→δv*
δm
δv
Viscosidad.
Existen fuerzas tangenciales: Fluidos Reales.
δuδt
τ →
u =δu
δθ
δy
La tensión es proporcional
a la deformación:
δθ
τ∝
δt
u= 0
Se puede hacer la siguiente aproximación para deformaciones pequeñas:
δθ ≈ tan δθ =
con esto se tiene que:
τ =µ
dθ
du
=µ
dt
dy
u
y
τ =µ
du
dy
δ uδ t
δy
⇒
Fluido Newtoniano.
dθ du
=
dt dy
µ coeficiente de viscosidad (viscosidad) .
[µ ] = FT2 = M
LT
L
µ
ν=
ρ
L2
Viscosidad cinemática. [ν ] =
T
Tensión superficial.
aire
Las partículas fluidas están sometidas a
fuerzas de cohesión lo que da lugar al
fenómeno de tensión superficial en la
separación de dos fluidos inmiscibles.
agua
Fσ
En el caso de una superficie alabeada, en general la
diferencia de presión entre los lados de la interface
depende de dos radios de curvatura.
Para superficies con curvatura la tensión
superficial se equilibra con las fuerzas debidas a
la diferencias de presión.
Fp
ρw
Si una superficie libre se limita por un contorno,
se puede medir la fuerza debida a la tensión
superficial. Y dicha fuerza por unidad de
longitud da el coeficiente de tensión superficial.
Fp
Ejemplos:
ρa
Fp
R1
L>>R
Fp = 2 LR ⋅ ∆p
∆p =
;
σ
L
Fσ = 2 Lσ
R2
Fσ
Fσ
dl1
Fp = π R 2 ⋅ ∆p
Fσ = 2π Rσ
;
∆p =
2σ
R
dl2
 1
1 
∆p = σ  + 
 R1 R2 
Estática. Presión.
La presión es una magnitud escalar que se puede definir como la relación entre el módulo de
una fuerza normal a una superficie y el área de la misma. Se cumple, para fuerzas normales:
r
r
F = pS
La presión es función de la posición por lo que se puede hablar de campo escalar de
presiones en le interior de un fluido.
S1 =α1S
3
S2
F2
F
F=pS
F1
F1 = p1 S1 = p1 α1 S
F2 = p2 S2 = p2 α2 S
F3 = p3 S3 = p3 α3 S
S1
S
S2 =α2S
S3 =α3S
2
Por equilibrio:
S3
1
F3
F1 =α1 F
F2 =α2 F
F α1 = p S α1 = p1 α1 S
F α2 = p S α2 = p2 α2 S
F α3 = p S α3 = p3 α3 S
F3 =α3 F
⇒ p = p1 = p2 = p3
Presión independiente de la orientación: escalar
Distribución espacial de la presión: Ley de Pascal.
p+
dz
1
∂p
dz
∂z
2
En las caras 1 y 2 la tensión normal es la presión en cada punto
la fuerza que actúa sobre cada cara será: pdxdz
Si existe equilibrio debe cumplirse:
∂p
p1dxdz = p2 dxdz = ( p1 + dy )dxdz
∂y
∂p
dxdydz = 0
∂y
dx
dy
p
∂p
=0
∂y
lo mismo debe cumplirse en la dirección x:
∂p
=0
∂x
En la dirección z, si consideramos que hay un campo gravitatorio el resultado es distinto.
∂p
dz )dxdy − ρ gdxdydz = 0
∂z
∂p
∂p
dxdydz = − ρ gdxdydz
= −ρ g
∂z
∂z
pdxdy − ( p +
Con densidad constante (fluido homogéneo)
con los resultados anteriores tendremos :
dp
= −ρ g
dz
⇒ ∆p = − ρ g ∆z
Ley de Pascal
p = p0 − ρ gz
∇p
∇p
ext
a
F
=
−
+
−
1
En general la ecuación de movimiento se debe escribir:
donde
ρ
ρ representan fuerzas
internas.
Ecuación de la Estática:
∇p
ext
F
=
1
a=0;
ρ
Aplicación de fuerzas de presión sobre cuerpos sumergidos: Principio de Arquímedes
En un cuerpo sumergido en un fluido de volumen V y rodeado por una superficie A, se puede conocer la fuerza
ejercida por el fluido sobre toda la superficie que rodea al cuerpo, a partir de la fuerza infinitesimal sobre un
elemento de superficie extendida a toda ella.
A
dA
dF
r
r
dF = − pdA
r
r
F = −Ñ
pdA
∫
A
p = p0 − ρ gz
V
⇒
r
r
F = Ñ∫ ρ gz dA
A
en caso de fluido homogéneo (densidad constante)
r
r
F = ρ g Ñ∫ zdA
A
Ñ∫
A
r
z dA
representa un vector cuyo módulo es el volumen rodeado por al
superficie A y su vector unitario es ∇ z
(Th. Gauss aplicado a un escalar)
Por tanto
r
r
F = ρ gV k
Principio de Arquímedes.
La fuerza resultante en un cuerpo sumergido de
densidad ρ’, teniendo en cuenta su peso y el empuje
(fuerza calculada anteriormente) es:
r
∑ F = Peso − Empuje = (ρ '− ρ)gV
Cinemática.
Descripción Lagrangiana
Se realiza en función del movimiento de las partículas que forman el fluido. Necesita
identificar dichas partículas utilizando coordenadas de numeración.
v( xn , y n , z n , t )
por ejemplo partícula que pasa por ( x1 , y1 , z1 ) en t = 0 :
v( x10 , y10 , z10 , t )
Descripción Euleriana:
Consiste en es estudio del movimiento según las velocidades de los puntos que
ocupa el fluido sin importar qué partículas están en cada instante en cada punto.
No reconoce a las partículas.
v( x, y , z , t )
Derivada sustancial de una magnitud (escalar o vectorial)
Caso de la velocidad
r
r
dv ∂v r r
=
+ v ⋅∇v
dt ∂t
r
∂v
derivada local
∂t
r r
v ⋅∇v termino advectivo.
d
∂ r
= + v ⋅∇
dt ∂t
r
Gradiente de la velocidad v :
 ∂vx

 ∂x
r  ∂v
∇v =  x
 ∂y
 ∂v
 x
 ∂z
∂v y
∂x
∂v y
∂y
∂v y
∂z






∂vz 

∂z 
∂vz
∂x
∂vz
∂y
Descripción del flujo (definiciones):
línea fluida: línea formada por una sucesión de partículas adyacentes.
trayectoria: Recorrido de una determinada partícula en el tiempo.
línea de traza: Línea fluida formada por las partículas que han pasado por determinado punto. (emitidas
desde un foco).
línea de corriente: Línea tangente al vector velocidad en cada punto para un instante dado.
Se cumple que
r
r r
r
v P dl con v = (u , v, w) y dl = ( dx, dy, dz)
por lo que existen proporcionalidad entre componentes
r
dl
dx dy dz
=
=
r =
v
u
v
w
tubo de corriente:
volumen encerrado por la superficie engendrada
por las líneas de corriente que se apoyan en una
línea fluida cerrada.
En flujo estacionario las líneas de corriente coinciden con
las trayectorias.
r
∂v
=0
∂t
t = to
r
v
DEFORMACIÓN EN UN FLUIDO.
Cuando en un sólido se aplican fuerzas externas se puede producir una deformación: Desplazamientos
relativos entre las partículas que lo forman.
En los fluidos la deformación que se produce se puede medir según la variación del campo de velocidades.
δvp
p
δs0
δr
O
δr
δsp
δv0
p
O
δsp= δs0 + δr ⋅ ∇s
δvp= δv0 + δr ⋅ ∇v
Deformación en el fluido
Deformación en el sólido
Sea
v = (u1 , u2 , u3 ) ; r = ( x1 , x2 , x3 )
 ∂u1

 ∂x1
 ∂u
∇v =  1
 ∂x 2
 ∂u1
 ∂x
 3
∂u 2
∂x1
∂u 2
∂x 2
∂u 2
∂x3
∂u 3 

∂x1 
∂u 3 

∂x 2 
∂u 3 
∂x3 
Tensor deformación de velocidad
Deformación lineal.
t
t + dt
A
u1
B
δ x1
A’
u1 +
∂u1
δ x1
∂x1
B’
(δ x1 ) '
u1dt


∂u1
δ x1  dt
 u1 +
∂x1


Deformación lateral.
t
∂u
u1 + 1 δ x2
∂x2
t + dt


∂u1
δ x2  dt
 u1 +
∂x2


dα
B’
B
δ x2
u dt
u1dt
A
u1
u2
C
δ x1
A
u2 +
∂u2
δ x1
∂x1
A’
dβ
C’
u2 dt


∂u2
δ x1  dt
 u2 +
∂x1


Los términos diagonales del tensor deformación representan las deformaciones lineales y
conjuntamente la variación relativa (deformación) volumétrica.
∂ui ∂u1 ∂u2 ∂u3
=
+
+
∂xi ∂x1 ∂x2 ∂x3
;
∂u
1 d
(δV ) = i
δV dt
∂xi
El resto de términos llevan las variaciones de forma y las rotaciones del fluido.
1  ∂u1 ∂u 2 


+
2  ∂x2 ∂x1 
→ Cambios de forma por unidad de tiempo. Variaciones laterales del campo
de velocidades (Cizallas)
1  ∂u 2 ∂u1 


−
2  ∂x1 ∂x2 
→
Rotación del fluido en el plano (1,2)
Llamamos vorticidad al vector
r
ω , que está relacionada con la velocidad según:
r
ω =∇×u
Con las componentes:
;
ω i = ε ijk
∂u k
∂x j
 ∂u ∂u 
 ∂u ∂u 
 ∂u
∂u 
ω1 =  3 − 2  ; ω 2 =  1 − 3  ; ω 3 =  2 − 1 
 ∂x2 ∂x3 
 ∂x3 ∂x1 
 ∂x1 ∂x2 
El tensor deformación es suma de los tres tensores vistos hasta ahora:
 ∂u1

 ∂x1

A= 0

 0


0
∂u 2
∂x2
0

0 


0 

∂u 3 
∂x3 


0

 1  ∂u
∂u 
B =   2 + 1 
 2  ∂x1 ∂x2 
 1  ∂u
∂u 
  3 + 1 
 2 ∂x
  1 ∂x3 
Se tiene que A + B =
Deformación Volumétrica
1  ∂u1 ∂u 2 


+
2  ∂x2 ∂x1 
0
1  ∂u 2 ∂u 3 


+
2  ∂x3 ∂x2 
∇v + ∇v
;
2
1  ∂u1 ∂u 3  


+
2  ∂x3 ∂x1  
1  ∂u 2 ∂u 3  

  ; Deformación lateral
+
2  ∂x3 ∂x2  


0


que representa la deformación del fluido propiamente.


0

 1  ∂u ∂u 
C =   1 − 2 
 2  ∂x2 ∂x1 
 1  ∂u ∂u 
  1 − 3 
 2 ∂x
  3 ∂x1 
1  ∂u 2 ∂u1 


−
2  ∂x1 ∂x 2 
0
1  ∂u 2 ∂u 3 


−
2  ∂x3 ∂x 2 
1  ∂u 3 ∂u1  


−
2  ∂x1 ∂x3  
1  ∂u 3 ∂u 2   ∇v − ∇v

 =
−
; Rotación
2  ∂x2 ∂x3  
2


0


Así el tensor gradiente de velocidad se puede poner como suma de los tensores A, B y C:
 ∂u1

 ∂x1
 ∂u
A+B+C= 1
 ∂x2
 ∂u1
 ∂x
 3
Tensor rotación también se puede escribir:
∂u 2
∂x1
∂u 2
∂x2
∂u 2
∂x3
 0
1
C =  − ω3
2
 ω2
∂u3 

∂x1 
∂u3 
 = ∇v .
∂x2 
∂u3 
∂x3 
ω3
0
− ω1
− ω2 

ω1 
0 
r
; 2C ≡ ( (ω ) ) = ( ( ∇ × v ) )
r
r
Por otra parte se cumple que δ r ⋅ ( (ω ) ) = ω × δ r , con lo que el campo de velocidades se puede
poner como:
 ∇v + ∇v 
 ∇v − ∇v 
v p = v 0 + δ r ⋅∇v = v 0 + δ r ⋅ 
 +δr ⋅
=
2
2




r
 ∇v + ∇v  δ r ⋅ ( (ω ) )
 ∇v + ∇v  δ r ⋅ ( ( ∇ × v ) )
v0 + δ r ⋅ 
+
=
v
+
r
⋅
δ


+
0
2
2
2
2




 ∇v + ∇v  1 r
vp = v 0 + δ r ⋅ 
 + (ω × δ r )
2

 2
donde los tres términos del último miembro representan:
v0
 ∇ v + ∇v 

δr ⋅ 
2


1 r
(ω × δ r )
2
traslación
deformación
rotación.
Vorticidad :
r
ω
r
r
r
ω = ∇ × u = rot u
Definimos circulación según: Γ =
Ñ∫
c
r
dl
r r
v ⋅ dl
r
r
r
r
v
S
r
por el teorema de Stokes se tiene: Ñ∫ c v ⋅ dl = ∫s rot v ⋅ ds
r r
es decir: Γ = ∫S ω ⋅ ds que representa el flujo de la vorticidad a través de la
superficie S
C
r
Cuando la vorticidad es cero se dice que el movimiento es irrotacional ω = 0
Ejemplos:
1. vórtice sólido
La velocidad angular es la misma en todo el fluido
ω0. utilizando coordenadas polares:
uθ = ω0 r
ur = 0
uz = 0
1 ∂
1 ∂ur
(r uθ ) −
= 2ω 0
r ∂r
r ∂θ
1. vórtice irrotacional.
y la vorticidad: ω z =
2. vórtice irrotacional.
La vorticidad en todos los puntos es cero excepto en el
origen.
uθ =
c
r
ur = 0
→ ωz =
0
=0
r
la vorticidad en el origen es ∞, ya que la circulación de v a
lo largo de cualquier línea cerrada que contiene el origen
O es finita y representa el flujo de la vorticidad.
c
r
Γ = 2π r ⋅ = 2π c ≠ 0 (finito)
ω ≠ 0 en algún punto (O )
r
→
r r
r r
Γ = Ñ∫ v ⋅ dl =∫ ω ⋅ ds (th. Stokes) ds → 0 ⇒ ω → ∞
Función de corriente
Se dice que un fluido es incompresible cuando se cumple:
1 dρ
=0
ρ dt
o alternativamente
1 dδ V
=0
δ V dt
no hay variación relativa de densidad
(o volumen específico)
1 dδ V
∂u
i
Según se ha visto en las deformaciones del fluido: δ V dt = ∂x
i
con lo que se puede decir que en fluidos incompresibles se cumple:
∂ui
=0
∂xi
r
∇ ⋅u = 0
ó
En movimiento plano:
∂u ∂v
+
=0
∂x ∂y
ó
∂u1 ∂u2 ∂u3
+
+
=0
∂x1 ∂x 2 ∂x3
con
∂w
=0
∂z
ó w=0
(1)
(flujo solenoidal).
Las componentes de la velocidad se pueden tener de la derivación de una función escalar según:
∂ψ
∂ψ
u=
; v=−
donde se cumple la ecuación (1) porque las derivadas
∂y
∂x
cruzadas son iguales:
∂u ∂v ∂ 2ψ ∂ 2ψ
+
=
−
=0
∂x ∂y ∂y∂x ∂x∂y
La función ψ se llama función de corriente
(Potencial de corriente)
ψ es constante a lo largo de las líneas de corriente
∂ψ
∂ψ
dx +
dy = 0
∂x
∂y
El flujo transcurre entre líneas de potencial de corriente constante.
Los valores mayores de ψ quedan a la izquierda del movimiento.
∇ψ =
r r
∂ψ r ∂ψ r
i+
j = −vi + uj
∂x
∂y
→
→
dψ = 0
r r
−vi + uj
r r
r
v = ui + vj
r
∇ψ ⊥ v
La diferencia de valores de dos líneas de corriente representan la
cantidad de fluido que atraviesa una línea transversal (C) en la
unidad de tiempo (Flujo de volumen):
r
r
2
2
2 r
ψ 2 − ψ 1 = ∫ dψ = ∫ ∇ ψ ⋅ dl = ∫ v × dl
1
1
Φ = ψ 2 −ψ1
1
ψ1
v
C
ψ2