Document

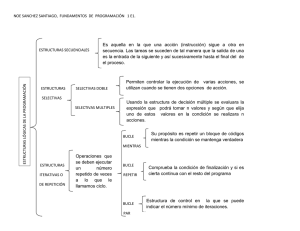
Práctica 2
Sentencias de control II
2.1
Objetivos
En esta tercera práctica se pretende que el alumno:
• Aprenda el uso básico del bucle “para” mediante la sentencia for de MATLAB.
• No puede hacer uso del bucle “hacer mientras”, mediante la sentencia while de MATLAB,
usado en la práctica anterior.
• Experimente con programas que contienen esta estructura cı́clica.
• Aplique la estructura a programas para el trazado de curvas y superficies.
Este enunciado contiene ejercicios suficientes para que se pueda aprovechar todo el tiempo
asignado a la sesión. Es decir, hay ejercicios de sobra. Tenga pues en cuenta que el objetivo
no es llegar al último ejercicio lo antes posible y marcharse. El objetivo es usar todo el tiempo
disponible para experimentar. Si se llega o no se llega a completar el último ejercicio es algo
que carece de importancia.
2.1.1
Requisitos
Se requiere que el alumno acuda a la sesión práctica con una copia de estas notas y con algún
documento identificación: DNI, permiso de conducción, tarjeta de la universidad, pasaporte,
etc.
Se requiere tener asimilados los conceptos de los diagramas de flujo con bifurcaciones y con
iteraciones o bucles correspondientes a las clases de teorı́a y problemas.
2.1.2
Desarrollo de la práctica
El alumno deberá realizar todos los puntos que se indican a continuación en el orden en que
aparecen.
1. Leer estas notas antes de la sesión práctica, despejando cualquier duda mediante consulta
a sus apuntes de clase.
2. Escribir en el entorno MATLAB todos los ejemplos que aparecen en estas notas, contemplando luego los resultados. Este proceso ha de realizarse de forma crı́tica, es decir, el
alumno ha de dedicar cierto tiempo a pensar porqué se obtienen esos resultados y no otros.
Es imprescindible que el alumno descubra por sı́ mismo sus errores y aprenda a corregirlos. No sirve de nada preguntar al profesor o al compañero en cuanto surge la menor duda
1
2
PRÁCTICA 2. SENTENCIAS DE CONTROL II
o dificultad. Antes de pasar al problema siguiente asegúrese que el programa que haya
creado funciona perfectamente y resuelve el problema planteado. Si fuese necesario use
clear all de forma adecuada para limpiar las variables al pasar de un ejercicio a otro.
3. Explorar ejemplos similares a los propuestos, cambiando alguna que otra cosa. En esas
pruebas debe ser capaz de predecir el resultado de los cambios introducidos. De este modo
aprenderá el uso de la herramienta MATLAB.
4. Resolver los ejercicios de auto-evaluación, comprobando la solución mediante pruebas en
el entorno de MATLAB.
2.2
La estructura cı́clica “para”
En muchas situaciones es preciso repetir una tarea un número conocido de veces, por ejemplo
para elevar un número a una potencia dada. En esas situaciones se puede construir un bucle
con un contador dando lugar al llamado bucle “para”.
El bucle “para” conlleva realizar una tarea varias veces. En cada pasada o repetición el
contador del bucle se modifica y se comprueba que no se ha sobrepasado el lı́mite. Estos bucles
se realizan fácilmente en MATLAB con el uso de la sentencia for. Los bucles que utilizan for
se codifican en MATLAB del siguiente modo:
for contador = valorinicial:valorfinal,
sentencias del cuerpo del bucle;
end
En la figura 2.1 a) se muestra el diagrama de flujo correspondiente al bucle anterior. En él
se observa que contador es una variable que sirve para controlar el bucle. Esta variable toma
inicialmente el valor especificado por valorinicial. La variable se incrementa al final de cada
pase o repetición en una unidad. La condición de salida del bucle consiste en que el contador
sobrepase el lı́mite fijado por el valor valorfinal.
A fin de aclarar las ideas se muestra el siguiente ejemplo de bucle usando la estructura
“para”.
for k = 1:6,
disp(k);
end
En la figura 2.1 b) se presenta el diagrama de flujo correspondiente a este ejemplo. Es fácil
ver que el bucle no realiza cálculo alguno, simplemente escribe en la pantalla los valores sucesivos
que va adquiriendo la variable k.
Este ejemplo revela porqué se le llama bucle “para”. Se observa que para cada valor de k
entre 1 y 6 se escribe k en la pantalla. La sentencia for k=1:6, precisamente indica para cada
valor de k entre 1 y 6. Tenga en cuenta que for y end son palabras del vocabulario reservado
de MATLAB por lo que no puede haber objetos ni archivos ni funciones con ese mismo nombre.
2.2.1
Variantes de la estructura “para”
Los valores iniciales y finales no necesariamente son constantes, pueden ser variables como en el
programa siguiente .
Informática, 1o Ing. Aeroespacial
Dpto. Ingenierı́a de Sistemas y Automática. E.T.S. Ingenieros. US. 3
inicio
Iniciar k a 1
Asignar al
contador el valor
inicial
no
¿ k
6 ?
no
sí
¿ contador dentro
de límites?
Escribir k
sí
k
k + 1
cuerpo
Actualizar el
contador
fin
Contador de 1 a 6
Valor inicial del contador
y valor para incrementar
Valor final del contador
a)
k
Variable entera
1
Variable entera
6
Variable entera
b)
Figura 2.1: a) Diagrama de flujo correspondiente a un bucle genérico del tipo “para”. b)
Diagrama de flujo correspondiente al ejemplo de uso del bucle “para”
% valores inicial y final para bucle
v_inicial = input(’Introduce valor inicial ’);
v_final
= input(’Introduce valor final ’);
% bucle
for k = v_inicial:v_final,
disp(k);
%escritura en pantalla
end
Grabe estas órdenes en un archivo y ejecute el programa varias veces con distintos valores,
comprobando su resultado.
El incremento de la variable contador puede ser distinto de uno, para saltar de dos en dos,
etc. La forma de indicar un incremento en la sentencia for es muy simple:
for contador = valorinicial:incremento:valorfinal,
sentencias del cuerpo del bucle;
end
A modo de ejemplo considere el programa:
for k=1:2:20,
disp(k);
end
Observará al ejecutarlo que se escriben en pantalla los números k desde el 1 al 20 avanzando de
dos en dos. Esta caracterı́stica puede servir por ejemplo para realizar una cuentra atrás:
4
PRÁCTICA 2. SENTENCIAS DE CONTROL II
for k=10:-1:0,
disp(k);
end
2.2.2
Ejercicio de aplicación
El bucle “para” es muy útil en el trazado de gráficas. Por ejemplo, para dibujar y = x2 − 5 con
x ∈ [−3, 3] se puede utilizar un bucle que calcule un vector vx = [−3, − 2.9, − 2.8, · · · , 3] de
abscisas y otro vector vy con sus ordenadas correspondientes: vyk = (vxk )2 − 5.
Resulta fácil comprobar que estos vectores tendrán un número de componentes n = 1 + (3 −
−3)/0.1 = 61, por tanto se puede hacer un bucle usando un ı́ndice k que variará entre 1 y 61.
Para probar el bucle “para”, copie las sentencias siguientes en un archivo de nombre graf1.m y
ejecute luego el programa.
for k=1:61,
vx(k)= -3 + 0.1*(k-1);
vy(k)= vx(k)*vx(k) - 5;
end
plot(vx, vy);
title(’graf1’);
Inspeccione ahora (mediante whos o por cualquier otro método que conciba) las componentes
del vector vx. Fı́jese que se han creado 61 componentes que van desde el -3 hasta el 3. Puede
ser útil añadirle a la gráfica una rejilla o cuadriculado que facilite su inspección. Para ello basta
con utilizar la orden de MATLAB grid. Puede escribirla en la ventana de órdenes en cualquier
momento o incluirla al final del programa en el archivo graf1.m.
2.2.3
Ejercicio propuesto
Como ejercicio escriba un programa de MATLAB que sirva para trazar la gráfica de y =sen(x3 )
con x ∈ [−2, 2]. La gráfica ha de constar de 201 puntos. Guarde el programa en un archivo de
nombre migrafsx3.m. En la figura 2.2 se muestra el aspecto que debe tener la gráfica para este
ejercicio. Si obtiene en su pantalla un resultado que no es el correcto debe repasar su programa.
2.3
Curvas polares
Una curva en coordenadas polares viene definida mediante una relación entre el radio o distancia
al origen (r) y el ángulo formado con el eje de abscisas (a), por ejemplo r = 1 y a ∈ [0, π] definen
una semi-circunferencia de radio 1 como se muestra en la figura 2.3.
Si se dispone de una curva polar del estilo r = f (a), a ∈ [aini , af in ] se puede realizar el trazado
en una ventana de MATLAB obteniendo dos vectores vx y vy en coordenadas cartesianas que
luego se dibujan uno frente al otro. Estos vectores se calculan sabiendo que cada punto de la
curva (r, a) tiene como coordenadas cartesianas (x, y) siendo x = r(a) · cos(a) e y = r(a) · sen(a).
A modo de ejemplo considere la espiral, que es una curva polar definida mediante: r(a) = θ/2
con a ∈ [0, 4π]. Para el dibujo se va a crear un vector de ángulos va tal que vak = 0.2·(k −1) con
k = 1, · · · , 64, este vector contiene los ángulos (0, 0.2, 0.4, · · · , 12.6), o sea que barre de forma
equiespaciada el intervalo [0, 4π] (aproximadamente). A partir de él se puede calcular un vector
de distancias polares vr tal que vrk = r(vak ) = vak /2. Con esto se han conseguido 64 puntos
de la curva polar. Ahora hay que pasar los puntos a coordenadas cartesianas, de este modo se
obtienen dos vectores vx y vy tales que vxk = vrk · cos(vak ) y vyk = vrk · sen(vak ). Finalmente
Informática, 1o Ing. Aeroespacial
Dpto. Ingenierı́a de Sistemas y Automática. E.T.S. Ingenieros. US. 5
graf2
1
0.8
0.6
0.4
0.2
0
−0.2
−0.4
−0.6
−0.8
−1
−2
−1.5
−1
−0.5
0
0.5
1
1.5
2
Figura 2.2: Gráfica correspondiente al programa graf2.m.
y
a
r
x
a)
Figura 2.3: Ejemplo de curva definida en coordenadas polares.
6
PRÁCTICA 2. SENTENCIAS DE CONTROL II
la espiral se dibuja mediante la orden plot(vx, vy, ’r’). El código siguiente permite realizar
la tarea en MATLAB.
for k=1:64,
va(k) = 0.2*(k-1);
end
for k=1:64,
vr(k) = va(k)/2;
end
for k=1:64,
vx(k) = vr(k)*cos( va(k) );
vy(k) = vr(k)*sin( va(k) );
end
plot(vx, vy, ’r’);
grid;
xlabel(’x’);
ylabel(’y’);
title(’espiral’);
Guarde las órdenes en un archivo de nombre espiral.m y ejecute luego el programa. Compruebe que se crean las variables con el valor correcto y que la curva en la ventana es la esperada.
Para hacer patente que la figura no es más que una sucesión de segmentos cambie el programa
y use la orden de dibujo plot(vx, vy, ’rx-’). Por si no queda lo bastante claro proceda a
modificar el programa para que el vector va contenga solamente 20 puntos al barrer el intervalo
[0, 4π]. Ejecute el programa y observe los cambios.
2.3.1
Ejercicio propuesto
Proceda de manera parecida al ejercicio anterior pero dibujando la cardioide que es una curva
que viene definida en coordenadas polares mediante: r(θ) = 1 − cos(θ) con θ ∈ [0, 2π]. Guarde
las órdenes en un archivo de nombre cardiode.m y ejecute luego el programa. Compruebe que
se crean las variables con el valor correcto y que la curva en la ventana es la esperada.
2.4
Matrices
Los bucles “para” son muy adecuados en problemas donde intervienen matrices. En tales casos
se usa un bucle dentro de otro, como ilustración observe el siguiente programa de MATLAB:
for k=1:7,
for j=1:3,
A(k,j)=k^2-j;
disp(A(k,j));
end
end
Intente dibujar el diagrama de flujo correspondiente a las operaciones que realiza. Una vez
conseguido esto escriba en un archivo de nombre matriza.m las sentencias anteriores. Ejecute
luego el programa, observará que el programa calcula y escribe una matriz A de siete filas y tres
columnas cuyo elemento genérico es Akj = k 2 − j. Si escribe la orden whos podrá comprobar
que la variable A existe y tiene las dimensiones correctas.
Informática, 1o Ing. Aeroespacial
Dpto. Ingenierı́a de Sistemas y Automática. E.T.S. Ingenieros. US. 7
Como ejemplo de aplicación de la doble iteración se va a crear un programa que calcule y
escriba S, el mayor elemento de una matriz cuadrada dada. Se supone que la matriz tiene de
nombre M y que cumple M ∈ IRn×n con n entero y n > 0. Se supone también que n es un valor
dado, por lo tanto el programa no ha de leer ni n ni M .
Dibuje el diagrama de flujo siguiendo los pasos aprendidos en el tema 6. Ahora codifique su
solución en MATLAB, grabe las órdenes en un archivo de nombre mimaxmatriz.m y pruebe el
resultado. Como es lógico antes de ejecutar el programa deberá crear una matriz M y dar un
valor adecuado a la variable n.
Si su solución no le convence del todo pruebe el código que se suministra a continuación.
Grabe las órdenes en un archivo de nombre maxmatriz.m y pruebe el resultado.
% máximo S de una matriz dada M de dimensión nxn, con n>0 dado
maxparc = M(1,1); % máximo parcial
for k=1:n,
for j=1:n,
if M(k,j) > maxparc,
maxparc = M(k,j); % actualización del máximo parcial
end
end
end
S=maxparc; % máximo
disp(S);
% escritura de S
2.5
Superficies
Es posible obtener gráficas de superficies usando la función mesh. En su forma más simple la
función mesh recibe una matriz que es interpretada como el conjunto de alturas z correspondiente
a una superficie z = f (x, y). A modo de ejemplo considere de nuevo la matriz Akj = k 2 − j. Al
programa que crea esta matriz se le van a añadir unas órdenes.
for k=1:7,
for j=1:3,
A(k,j)=k^2-j;
end
end
mesh(A);
xlabel(’ı́ndice j’);
ylabel(’ı́ndice k’);
zlabel(’alturas’)
Grabe estas órdenes en un archivo de nombre superf1.m y ejecute el programa. Verá que
aparece una ventana de dibujo donde se aprecia una superficie construida con trozos rectangulares. Puede girar la superficie usando uno de los botones de dicha ventana y el ratón. De este
modo comprobará que la gráfica es una representación en la pantalla de un objeto tridimensional.
A fin de aclarar el uso de mesh considere el problema de trazar la superficie de la función
z = x + 0.5 · y que es un plano que pasa por el origen. Escriba el siguiente programa en un
archivo de nombre plano.m y ejecútelo para comprobar su funcionamiento.
for k=1:15,
for j=1:30,
8
PRÁCTICA 2. SENTENCIAS DE CONTROL II
z(k,j) = k + 0.5*j;
end
end
mesh(z);
xlabel(’j’);
ylabel(’k’);
title(’Superficie plana’);
Gire la superficie usando el ratón y compruebe que se trata de un plano. Los colores de la
rejilla que forma la superficie representan alturas. Para verlo más claro escriba colorbar; y
verá aparecer una barra con la gradación de colores. Los colores pueden cambiarse a voluntad,
pero existen ciertas combinaciones predefinidas. Pruebe las siguientes: colormap(’gray’);
colormap(’copper’); colormap(’cool’);.
Como puede verse, la función mesh es parecida a plot, pero permite trazar superficies. Las
componentes de la matriz se interpretan como alturas (eje z), los subı́ndices k y j son interpretados como la posición sobre los ejes y y x respectivamente. Gracias a esta función de MATLAB
es posible trazar de forma cómoda superficies correspondientes a funciones matemáticas del tipo
z = f (x, y) siendo f : IR2 → IR.
2.5.1
Ejercicio propuesto
Modifique el programa anterior para que se calcule (calcular sólo, no escribir) una matriz B con
número de filas m = 20 y número de columnas n = 30 y con elemento genérico:
Bkj = sen(k/7) · cos(j/7)
Guarde el programa con el nombre misencos.m. Ejecútelo y compruebe mediante la orden
whos que la matriz ha sido creada con las dimensiones correctas. Una vez hecho esto escriba en
la ventana de órdenes de MATLAB la orden mesh(B). El resultado ha de ser similar al mostrado
en la figura 2.4.
1
0.5
0
−0.5
−1
20
30
15
25
10
20
15
5
10
5
0
0
Figura 2.4: Superficie formada por los elementos de bkj = sen(k/7) · cos(j/7) tomados como
alturas (eje z) frente a sus ı́ndices k y j
Informática, 1o Ing. Aeroespacial
2.6
Dpto. Ingenierı́a de Sistemas y Automática. E.T.S. Ingenieros. US. 9
Ejercicios de autoevaluación
2.6.1
Ejercicio 1
Enunciado: Se le proporciona una variable n entera y n > 2. Debe calcular una matriz A de
dimensión n × n cuyas componentes sean unos o ceros dependiendo de su posición. Las
componentes Akj valdrán 1 si k + j es par y cero en caso contrario. Introduzca el trozo de
código que resuelve el problema.
Discusión: No se pide que se lea ninguna variable ni que se escriba ninguna variable. Solamente
se pide que se calcule A siguiendo una regla dada y con las dimensiones adecuadas.
Solución: El problema se resuelve con un algoritmo que puede representarse con un diagrama
de flujo con dos bucles, como los que aparecen en el tema 6. La codificación del algoritmo
en MATLAB es:
valorini = 0;
for k=1:n,
valor = valorini;
for j=1:n,
A(k,j) = valor;
if valor ==0,
valor =1;
else
valor =0;
end
end
if valorini ==0,
valorini =1;
else
valorini =0;
end
end
Intente crear el diagrama de flujo que corresponde a esta codificación y compruebe su
funcionamiento sobre el papel.
Comprobación: Para comprobar que la codificación es correcta puede usar el entorno de MATLAB. Para ello puede proceder del siguiente modo: proporcione a n un valor factible y
luego ejecute el código de la solución. Compruebe luego que las componentes de A son
correctas. Repita la comprobación para otros valores de n hasta que quede convencido del
buen funcionamiento.
10
2.7
PRÁCTICA 2. SENTENCIAS DE CONTROL II
Ejercicios propuestos adicionales
Recuerde que todos los ejercicios han de resolverse mediante bucles for necesariamente y no
con while.
2.7.1
Ejercicio propuesto 1.
Dado un vector v ∈ IR1×n , se pide que desarrolle el código que calcule la suma
s=
k=n
X
(vk2 − m)
k=1
siendo m la media de las componentes del vector. Se supone que n es un número entero n > 0
dado, por lo que el programa no tiene que leer nada.
2.7.2
Ejercicio propuesto 2.
Se desea calcular la suma dada por
s=
n
X
1
kn
k=1
siendo n un número entero n > 0 dado, por lo que el programa no tiene que leer nada. Desarrolle
el código que resuelve el problema.
2.7.3
Ejercicio propuesto 3.
Dada una matriz A ∈ IRm×n con m > 1 y n > 1 dados, se desea calcular un vector columna
v ∈ IRm cuya componente genérica vk es el mayor valor de la fila k−ésima de A. Se supone que
A, m y n son valores dados por lo que el programa no tiene que leer nada. Desarrolle el código
que resuelve el problema.
2.7.4
Ejercicio propuesto 4.
Dada una matriz A ∈ IRm×n con m > 1 y n > 1 dados, se desea calcular otra matriz B ∈ IRm×n
cuyos elementos son todos cero excepto los de la submatriz triangular superior que son iguales a
los elementos de igual posición de A. Es decir, los elementos que están por encima de la diagonal
principal de A se copian en B, el resto de elementos de B valen cero.
A modo de ejemplo sea
1 2 3
0 2 3
A=
, B=
.
4 5 6
0 0 6
Se supone que A, m y n son valores dados por lo que no tiene que leer nada. Desarrolle el código
que resuelve el problema.