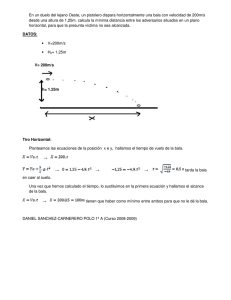
Una bala de cañón se dispara horizontalmente con una velocidad
Anuncio

Una bala de cañón se dispara horizontalmente con una velocidad de 120m/s, desde lo alto de un acantilado de 250m de altura, sobre el nivel de un lago, tal como se muestra en la figura. A. ¿Qué tiempo tarda la bala en caer al agua? B. ¿Cuál será la distancia horizontal que del pie del acantilado al punto de impacto de la bala? C. ¿Cuáles son las componentes horizontal y vertical de la velocidad de la bala cuando cae al agua? Los datos del problema son: Vx = 120 m/s Voy = 0 (la bala sale horizontalmente) Yo = 250 m tc = ? Xmax = ? V=? Velocidad con que impacta en el agua a) Tomemos como punto de referencia el suelo, justo el instante en que se suelta la esfera. Por Cinemática del Tiro Parabólico sabemos: Y = Yo + Voy*t - ½ gt^2 Cuando y = 0 ----- t = tc 0 = 250 + 0 - ½ (9.8)(tc)^2 0 = 250 -4,9*tc^2 tc^2 = 51,02 tc = 7,14 s Este es el tiempo que tarda la bala en llegar al agua. b) La bala sale horizontalmente a 120 m/s , la velocidad en el eje x en el movimiento parabólico es constante durante toda la trayectoria. X = Vx*t Cuando t = tc ---------- x = Xmax Xmax = Vx*tc Xmax = 120 m/s * 7,14s Xmax = 857,14 m c) Por Cinemática del movimiento parabólico sabemos: Vy = Voy*t – gt Para t= 7,14s Vy = 0 -(9,8)(7,14) Vy = -69,97m/s tienen sentido vertical hacia abajo el signo “-“ significa que la velocidad Además por lo dicho en b) sabemos que Vx = 120m/s Vx β Vy V La velocidad en a los 5 segundos es 𝑉 = 𝑟𝑎í𝑧(𝑉𝑥 2 + 𝑉𝑦 2 ) 𝑉 = 𝑟𝑎í𝑧 (1202 + (−69,97)2 ) 𝑉 = 138,9 𝑚 𝑠 𝑉𝑦 𝑇𝑔𝐵 = 𝑉𝑥 𝑇𝑔𝐵 = − 69,97 120 β = -30,25º = -0,5831