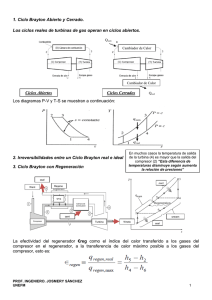
Brayton Cycle - Gas

2009
UTO - FNI
Dpto. Ing. Mecánica
Ciclos de Potencia de Gas
Turbinas de Gas
Emilio Rivera Chávez
Apuntes de Clase
Apuntes de Clase
Docente: Emilio Rivera Chávez
George Brayton (1830-1892), U.S. mechanical engineer and
pioneer in the development of internal combustion engines, invented the continuous ignition combustion engine that later became the basis for the turbine engine. He is believed to be first
in the United States to manufacture and sell gas turbines commercially (in the Providence, Rhode Island, area). He began
working on internal combustion engines in the 1870s. His internal combustion engine contained a diaphragm through which
flame entered the water-cooled cylinder, creating poor combustion (George B. Selden later patented an engine identical to
Brayton's except that it omitted the diaphragm). He was born
Oct. 3, 1830, Rhode Island, and died Dec. 17, 1892, London,
England.
http://www.braytonenergy.net
http://www.asme.org/Communities/History/Resources/Brayton_George.cfm
Brayton's Ready Motor
In 1872 Brayton patented a two-stroke kerosene stationary engine known
as Brayton's Ready Motor,[2] which had one cylinder for compression, a
combustion chamber, and a separate cylinder in which the products
expanded for the power stroke. It bore a marked resemblance to a steam
engine with its rocking beam and flywheel. His engine needed no spark
plug - it had a continuously burning flame to ignite each cycle of the
engine.[3] He demonstrated that prolonging the combustion phase of the
cycle, by injecting fuel at a controlled rate, produced more power per unit
of fuel consumed. However, much of the efficiency gained by this
method was lost due to the lack of an adequate method of compressing
the fuel mixture prior to ignition.
Brayton's engine was displayed at the Centennial Exposition in
Philadelphia in 1876 and for a few years was well regarded, but within a
short time the Otto engine became more popular. However, it was
considered the first safe and practical oil engine and also served as
inspiration to George B. Selden.
A Brayton Engine is preserved in the Smithsonian in the American History museum, and a later Brayton engine
which powered one of John Philip Holland's early submarines is preserved in the Great Falls Museum in Paterson,
New Jersey.[4]
References
http://en.wikipedia.org/wiki/George_Brayton
1. Hopkins, Hannah Clarke Bailey, Records of the Bailey family : descendants of William Bailey of Newport, R.I.,
chiefly in the line of his son, Hugh Bailey of East Greenwich, R.I. Providence, R.I.: unknown, 1895, p. 75-6.
2. "IMPROVEMENT IN GAS-ENGINES (Patent no. 125166)". Google Patent Search.
http://www.google.com/patents?id=vWlxAAAAEBAJ&dq=george+brayton+1872. Retrieved 2007-07-29.
3. ^ "George Brayton's Engine". Today In Science History.
http://www.todayinsci.com/B/Brayton_George/BraytonGeorgeEngine2.htm. Retrieved 2007-07-29.
4. ^ "Holland Submarines". Paterson Friends of the Great Falls.
http://patersongreatfalls.com/0325pgf/00a.cgi?cr=12a01a00&hd=dhd&ft=dft. Retrieved 2007-07-29.
Ciclos de Turbinas a Gas
Página | 1
Apuntes de Clase
Docente: Emilio Rivera Chávez
Presentación
Una turbina de gas, también llamada turbina de combustión, es una turbo-máquina que extrae energía de
un flujo de gases de combustión. Tiene un compresor acoplado a una turbina y una cámara de
combustión entre ambos dispositivos. Las turbinas de gas se utilizan en diversas aplicaciones: producción
de electricidad, buques, locomotoras, helicópteros y en tanques. El uso de turbinas de gas en tanques
militares ha tenido mucho éxito. Varias clases de locomotoras han sido impulsadas por turbinas de gas.
Las turbinas de gas se describen termodinámicamente por el ciclo de Brayton. El ciclo de Brayton es un
proceso cíclico generalmente asociado con la turbina de gas. Como otros ciclos de potencia de
combustión interna es un sistema abierto, aunque para el análisis termodinámico es una suposición
conveniente asumir que los gases de escape son reutilizados en la aspiración, lo que posibilita el análisis
como un sistema cerrado. Fue nombrado por George Brayton, y es también conocido como ciclo de Joule
Un motor de tipo Brayton consta de tres componentes: un compresor de gas, una cámara de mezcla, un
expansor. El termino ciclo Brayton ha sido aplicado posteriormente al motor de turbina de gas. Este
también tiene tres componentes: un compresor de gas, un quemador (o cámara de combustión), una
turbina de expansión. El Aire ambiente es introducido en el compresor, donde es presurizado, en un
proceso teóricamente isentrópico. El aire comprimido a continuación, se conduce a través de una cámara
de combustión, donde se quema combustible, calentando este aire, en un proceso presión constante, ya
que la cámara está abierta a la entrada y salida de flujo. El aire caliente, presurizado, a continuación,
cede su energía, al expandirse a través de una turbina (o una serie de turbinas), otro proceso
teóricamente isentrópico. Parte del trabajo extraído por la turbina se utiliza para impulsar el compresor
En este capítulo nos ocuparemos de estudiar los procesos termodinámicos implicados en las turbinas de
gas desde un punto de vista esencialmente teórico.
Introduction
A gas turbine, also called a combustion turbine, is a rotary engine that extracts energy from a flow of
combustion gas. It has an upstream compressor coupled to a downstream turbine, and a combustion
chamber in-between. Gas turbines are used on several purposes: electrical generation, ships,
locomotives, helicopters, and in tanks. Use of gas turbines in military tanks has been more successful.
Several locomotive classes have been powered by gas turbines.
Gas turbines are described thermodynamically by the Brayton cycle. The Brayton cycle is a cyclic process
generally associated with the gas turbine. Like other internal combustion power cycles it is an open
system, though for thermodynamic analysis it is a convenient fiction to assume that the exhaust gases are
reused in the intake, enabling analysis as a closed system. It named for George Brayton, and is also
known as the Joule cycle.
A Brayton-type engine consists of three components: A gas compressor, A mixing chamber, An expander.
The term Brayton cycle has more recently been given to the gas turbine engine. This also has three
components: A gas compressor, A burner (or combustion chamber), An expansion turbine Ambient air is
drawn into the compressor, where it is pressurized, a theoretically isentropic process. The compressed air
then runs through a combustion chamber, where fuel is burned, heating that air, a constant-pressure
process, since the chamber is open to flow in and out. The heated, pressurized air then gives up its
energy, expanding through a turbine (or series of turbines), another theoretically isentropic process. Some
of the work extracted by the turbine is used to drive the compressor.
In this chapter we will look into studying the processes involved in gas turbines from a theoretical view
point.
Ciclos de Turbinas a Gas
Página | 2
Apuntes de Clase
Docente: Emilio Rivera Chávez
TURBINAS A GAS
GAS TURBINES
Generalidades
Generalities
La turbina de gas es un dispositivo diseñado
para extraer energía química de un fluido que
fluye a su través y transformarla en energía
mecánica.
The gas turbine is a designed device to extract
chemical energy of a fluid that flows through it
and to transform it into mechanical energy.
Las dos principales áreas de aplicación de la
turbinas de gas son la propulsión de aviones y la
generación de energía eléctrica.
The two main areas of application of the gas
turbines are the propulsion of airplanes and the
generation of electrical energy.
Las turbinas de gas usualmente operan en un
ciclo abierto, como muestra la figura 1. Aire
fresco en condiciones ambiente se introduce
dentro del compresor donde su temperatura y
presión se eleva. El aire a alta presión va a la
cámara de combustión donde el combustible se
quema a presión constante. Luego los gases
resultantes a alta temperatura entran a la turbina, donde se expanden hasta la presión atmosférica, de tal forma que producen potencia.
Los gases de escape que salen de la turbina se
expulsan hacia fuera (no se recirculan), por ello
el ciclo se clasifica como un ciclo abierto. Este
ciclo de turbina de gas abierto puede modelarse
como un ciclo cerrado, del modo que se muestra
en la figura 2, mediante las suposiciones de aire
estándar.
The gas turbines usually operate in an opened
cycle, as it shows figure 1. Fresh air in ambient
conditions is introduced inside the compressor
where its temperature and pressure increase.
The air to high pressure goes to the combustion
chamber where the fuel is burned to constant
pressure. Then the resulting gases to high temperature enter to the turbine, where they expand
until the atmospheric pressure, of such form that
produces power. The exhaust gases that leave
the turbine expel towards outside (they are not
recirculated), It causes that the cycle is classified
like an open cycle. This cycle of open gas turbine just can be modeled like a closed cycle, of
the way that is show in the figure 2, by means of
the standard air suppositions.
En este caso los procesos de compresión y
expansión permanecen iguales, pero el proceso
de combustión se sustituye por un proceso de
adición de calor a presión constante de una
fuente externa, y el proceso de escape se reemplaza por uno de rechazo de calor a presión
constante hacia el aire ambiente. El ciclo ideal
que el fluido de trabajo experimenta en este ciclo
cerrado es el ciclo Brayton, que esta integrado
por cuatro procesos internamente reversibles:
In this case the processes of compression and
expansion remain equal, but the combustion
process is replaced by a process of heat addition
constant pressure of an outsourcing, and the
escape process is replaced by one of heat reject
to constant pressure towards the ambient air.
The ideal cycle that the work fluid experiments in
this closed cycle is the Brayton cycle, that this
integrated
by
four
internally
reversible
processes:
Ciclos de Turbinas a Gas
Página | 3
Apuntes de Clase
Docente: Emilio Rivera Chávez
1-2 Compresión isentrópica (en un compresor).
2-3 Adición de calor a presión constante.
3-4 Expansión isentrópica (en una turbina).
4-1 Rechazo de calor a presión constante.
1-2 isentropic compression (in a compressor)
2-3 Heat Addition to constant pressure.
3-4 Isentropic Expansion (in a turbine).
4-1 Heat Rejection to constant pressure.
El fluido de trabajo en ciclo cerrado entra al
intercambiador de calor de temperatura elevada
en el estado 2, donde se le agrega energía a un
proceso de presión constante, hasta que alcanza la temperatura elevada del estado 3. Entonces, el fluido entra a la turbina y tiene lugar una
expansión isentrópica, produciendo cierto trabajo. El fluido sale de la turbina al estado 4 y pasa
a ser enfriado, en un proceso a presión constante, en el intercambiador de calor de baja temperatura, de donde sale al estado 1, listo para
entrar al compresor, y el ciclo se repite.
----------------------------------------------
The fluid of work in closed cycle enters the heat
exchanger of elevated temperature state 2,
where energy to a process of constant pressure
is added to him, until it reaches the elevated
temperature of state 3. Then, the fluid enters the
turbine and takes place a isentropic expansion,
producing certain work. The fluid leaves the
turbine to state 4 and happens to be cooled, in a
process to constant pressure, the heat exchanger of low temperature, where it leaves to state 1,
ready to enter the compressor, and cycle is
repeated.
-----------------------------------------------
Compresor
El compresor comprime el aire entrante hasta cerca
de 5 o 6 veces la presión atmosférica. Generalmente
en turbinas grandes, se utilizan compresores axiales,
en lugar de los compresores radiales o centrífugos.
Se comprime el aire pues la combustión del aire comprimido y del combustible es más eficiente que la
combustión del aire sin comprimir y del combustible.
Compresor
The air compressor compresses the incoming air to
about 5 or 6 times atmospheric pressure. Generally in
larger turbines, axial compressors are used, as opposed to radial or centrifugal compressors.
The air is compressed as the combustion of compressed air and fuel is more efficient than the combustion of uncompressed air and fuel.
Cámara de Combustión
Es el lugar donde el combustible es quemado junto al
aire presurizado del compresor. Esquemáticamente la
cámara de combustión se representa como un objeto
rectangular, cuando de hecho allí están generalmente
pequeñas y numerosas cámaras de combustión alrededor de la superficie externa cilíndrica del cuerpo del
compresor. Las cámaras de combustión a veces se
llaman las “latas”, ¡porque son realmente eso – cajas
de metal huecas y vacías! El combustible se inyecta
en la cámara a alta presión y el combustor esta construido para mezclar de manera óptima el aire presurizado con el combustible para la combustión completa.
Combustion Chamber.
This is the region where the fuel is combusted with
the pressurized air from the compressor. The schematic represents the combustion chamber as a rectangular object, when if fact there are generally numerous small combustion chambers around the cylindrical outer surface of the compressor body. The
combustion chambers are sometimes called 'cans',
because they are really just that - hollow empty metal
boxes! The fuel is injected into the chamber at high
pressure and the combustor is shaped so as to optimally mix the pressured air and fuel for complete
combustion.
Turbina.
El único propósito de la turbina en el motor de turbina de gas de un turborreactor, es proporcionar la
energía mecánica en el eje para rotar el compresor.
(La corriente de aire acelerada que propulsa el avión).
Bien, pero eso no es verdad para otros usos de la
turbina de gas. En el avión “turbopropulsor” el
avión es propulsado por una corriente de aire acelerada, pero esa corriente aérea es generada por un
propulsor que rota - aquí la turbina debe proporcionar
la energía mecánica para el compresor y el propulsor.
Turbine.
The only purpose of the turbine in turbo-fan gas
turbine engine, it to provide the mechanical shaft
energy to rotate the compressor. (It was the accelerated airstream that propels the aircraft)
Ok, but that's not true for other gas turbine applications. In 'turbo-prop' aircraft the aircraft is propelled
by a accelerated airstream, but that airstream is generated by a rotating propeller - here the turbine must
provide mechanical shaft energy for both the compressor and propeller.
.
Ciclos de Turbinas a Gas
Página | 4
Apuntes de Clase
Docente: Emilio Rivera Chávez
Ciclo Brayton - Turbina de Gas
Brayton Cycle - Gas-Turbine Engine
El Ciclo Brayton es un proceso cíclico asociado generalmente a una turbina a gas. Al igual
que otros ciclos de potencia de combustión interna, el ciclo Brayton es un sistema abierto,
aunque para un análisis termodinámico es conveniente asumir que los gases de escape son
reutilizados en el ingreso, permitiendo el análisis
como sistema cerrado.
The Brayton cycle is a cyclic process generally
associated with the gas turbine. Like other
internal combustion power cycles it is an open
system, though for thermodynamic analysis it is a
convenient fiction to assume that the exhaust
gases are reused in the intake, enabling analysis
as a closed system.
A Brayton engine consists of three components:
Un motor Brayton esta compuesto por tres componentes:
 Un compresor
 Un quemador (o cámara de combustión )
 Una turbina



A compressor
A burner (or combustion chamber)
A turbine
.
Ciclo Brayton Idealizado
(Idealized Brayton Cycle)
qA
qA
wn
wc
qR
qR
Gases de
combustión
Diagrama de bloques
Diagrama p-v
Diagrama T-s
FIGURA 3
Proceso
Descripción
Description
1-2
Compresión isentrópica del aire que se
introduce a la cámara de combustión del
motor.
Isentropic-compression of the intake air
into the combustion section of the engine.
2-3
Combustión a presión constante del
combustible inyectado en la cámara de
combustión.
Constant-pressure combustion of fuel
injected into combustion chamber.
3-4
Expansión isentrópica en la sección de la
turbina. Ésta es la parte del ciclo que
hace el trabajo positivo.
Isentropic-expansion through the turbine
section. This is the part of the cycle that
does positive work.
4-1
Calor a presión constante es evacuado
en el aire.
Constant-pressure heat is exhausting
into the air.
Ciclos de Turbinas a Gas
Página | 5
Apuntes de Clase
Docente: Emilio Rivera Chávez
El aire ambiente se introduce dentro de compresor, donde se presuriza –en un proceso
teóricamente isentrópico. El aire comprimido
entonces ingresa a través de una cámara de
combustión, en donde se quema un combustible, calentando ese aire- en un proceso a
presión constante, puesto que la cámara esta
abierta para el flujo de entrada y salida. El aire
caliente, presurizado cede entonces su energía, el expandirse en una turbina (o la serie de
turbinas) – otro proceso teóricamente isentrópico-. Una parte del trabajo extraído por la
turbina se utiliza para accionar el compresor.
Ambient air is drawn into the compressor,
where it is pressurized—a theoretically
isentropic process. The compressed air then
runs through a combustion chamber, where
fuel is burned, heating that air—a constantpressure process, since the chamber is open
to flow in and out. The heated, pressurized air
then gives up its energy, expanding through a
turbine (or series of turbines)—another
theoretically isentropic process. Some of the
work extracted by the turbine is used to drive
the compressor.
Desde ya ni la compresión ni la expansión
pueden ser realmente isentrópicos, las pérdidas de energía a través del compresor y la
turbina representan fuentes inevitables de las
ineficacias en el funcionamiento.
Since neither the compression nor the
expansion can be truly isentropic, losses
through the compressor and the turbine
represent sources of inescapable working
inefficiencies.
En general, el incremento de la relación de
compresión es la manera más directa de
aumentar la salida de energía total de un Sistema de Brayton.
In general, increasing the compression ratio
is the most direct way to increase the overall
power output of a Brayton system.
Rendimiento Térmico
Thermal efficiency
El rendimiento del ciclo de Brayton de aire
estándar está dado por:
The efficiency of the standard air Brayton cycle
is given by:
 term.  1 
qR
qA
1 
c p (T4  T1 )
c p (T3  T2 )
Si asumimos que la compresión (1-2) y la
expansión (3-4) son procesos isentrópicos,
podemos escribir:
P2  T2 
 
P1  T1 
1
T1 (T4 / T1  1)
T2 (T3 / T2  1)
Assuming that the compression (1-2) and
pansion (3-4) are isentropic processes, we can
write:
k /( k 1)
P3  T3 
 
p4  T4 
;
k /( k 1)
El diagrama p-v (Figura 3), muestra que
p-v Diagram (Figure 3),
shows that
P3 P2
p
P
  3 4
P4 P1
P2 P1
en consecuencia, se tiene
 T2

 T1
as a result, has



k /( k 1)
T
  3
 T4



k /( k 1)
term.  1 
Ciclos de Turbinas a Gas

T
T4 T3
T4


1  3 1
T1 T2
T1
T2
T1 (T4 / T1  1)
T
 1 1
T2 (T3 / T2  1)
T2
Página | 6
Apuntes de Clase
Docente: Emilio Rivera Chávez
finalmente se tiene que
 term
p 
 1   1 
 p2 
finally
 k 1 / k
 1
1
r 
p
donde
k 1
k
where
es la relación de presión.
p
rp  2
p1
is the pressure ratio
En consecuencia, bajo la hipótesis de aire frio
estándar la eficiencia térmica de un ciclo
Brayton ideal depende de la relación de presiones, rp, y de la relación de calores específicos, k, del fluido de trabajo.
Consequently, under the hypothesis of air
standard cold thermal efficiency of an ideal
Brayton cycle depends on’s pressure ratio rp
and specific heat ratio k of working fluid.
FIGURA 4
La eficiencia térmica del ciclo Brayton ideal
aumenta con la relación de presión, esto también es cierto para las turbinas reales.
Ejemplo 1.
Calcúlese la eficiencia térmica de un ciclo de
aire estándar de Brayton para las siguientes
razones de presión: 4, 6, 8, 10, 12 Y 14. Grafíquese la eficiencia térmica del ciclo contra la
relación de presiones. ¿Cuál es la razón de
presiones correspondiente a la máxima eficiencia?
 term  1 
1
r 
p
4
6
8
10
12
14
Ƞciclo
0.327
0.400
0.448
0.482
0.508
0.530
Eficiencia térmica vs. Relación de presión
Eficiencia térrmica, ƞ
rp
k 1
k
Relación de presiones, rp
Ciclos de Turbinas a Gas
Página | 7
Apuntes de Clase
Docente: Emilio Rivera Chávez
Trabajo neto del ciclo Brayton ideal
Net work ideal Brayton cycle
El trabajo neto durante el ciclo está dado por:
The net work done by the cycle is
wneto  wturb  wcomp
 c p (T3  T4 )  c p (T2  T1 )
Esta ecuación puede ser expresada como un
función de la relación de presión, así:
This equation can be written as a function of
the relationship of pressure, thus:

1 
( k 1) / k
Wneto  c p T3 1  k  1 / k   c p T1 rp
1
 rp



Es decir que, para un ciclo Brayton ideal operando entre dos límites de temperatura dados,
el trabajo neto desarrollado durante el ciclo
depende únicamente de la relación de presiones.
It is to say that, for ideal a Brayton cycle operating between two given limits of temperature,
the developed net work during the cycle depends exclusively on the relation of pressures.
Relación de presión óptima del ciclo
Brayton ideal
Optimal ratio of pressure ideal Brayton
cycle
rp1
FIGURA 5
Para una temperatura de entrada fija de la
turbina T3, la salida de trabajo neto por ciclo
aumenta con la relación de presiones, hasta
alcanzar un valor máximo y después empieza
a disminuir.
rp 2
rpo p t
wnet1  wnet,max  wnet 2
Para valores dados de T3 y T1, la relación de
presión óptima, que maximiza el trabajo se
obtiene a partir de:
For fixed T3 and T1, the pressure ratio that
makes the work a maximum is obtained from:
wneto
0
rp
(k-1)/k
Esto es más fácil si hacemos Z = rp
(k-1)/k
This is easier to do if we let Z = rp
 1
wneto  c p T3 1    c pT1 Z  1
 Z
wneto
1

 c pT3 0  2   c pT1 1  0  0
Z
Z 

Ciclos de Turbinas a Gas
Página | 8
Apuntes de Clase
Docente: Emilio Rivera Chávez
Solving for Z
despejando para Z
T 
Z   3 
 T1 
1/ 2
Entonces, la rp que hace que el trabajo neto
sea máximo para calores específicos constantes y valores fijos de T3 yT1 es
rpopt
Then, the rp that makes the work a maximum
for the constant property case and fixed T3 and
T1 is
T 
  3 
 T1 
k / 2 ( K 1)
Where: T3 and T1 are the maximum and minimum temperature of the cycle.
Donde T3 y T1 son la temperatura máxima y
mínima del ciclo.
Ejemplo 2
Un ciclo de aire estándar de Brayton opera
entre dos límites de temperatura de 80 y 1600
0
F. Calcúlese el trabajo neto desarrollado por
el ciclo, en Btu/lbm, para las siguientes relaciones de presión: 4, 6, 8, 10, 12 y 14. Grafíquese el trabajo neto producido contra la relación de presiones. ¿Cuál es la razón de presiones para el máximo trabajo neto?
Par las condiciones planteadas en el problema, el trabajo
neto desarrollado por la turbina esta dado por:
wneto 
wturb

wcomp
wneto  c p (T3  T4 )  c p (T2  T1 )
Donde T2 y T4 están dadas por
k  1/ k
Los resultados obtenidos se muestran en la
mismos que se grafican a la derecha.
rp
4
6
8
10
12
14
T2
R
802
901
978
1043
1098
1148
T4
wt
wc
Ciclos de Turbinas a Gas
T4 
T3
rp
k  1/ k
tabla,
wn
R
Btu/lbm Btu/lbm Btu/lbm
98.7
1386 161.7
63.0
1235 198.1
86.6 111.4
1137 221.5 105.2 116.3
1067 238.3 120.6 117.7
1013 251.3 134.0 117.3
969 261.8 145.9 115.9
El trabajo neto máximo se produce para rp=10
;
Trabajo Neto, wn
T2  T1rp
wn,max
Relación de presión, rp
Página | 9
Apuntes de Clase
Docente: Emilio Rivera Chávez
Ejemplo 3
o
Un ciclo Brayton ideal de aire estándar opera con aire que ingresa al compresor a 95 kPa y 22 C. La
razón de presión es 6 y sale del proceso de adición de calor a 1100 K, Calcule de trabajo del compresor y
el trabajo de la turbina por unidad de flujo másico, la eficiencia del ciclo, la razón de trabajo de retroceso.
Asuma calores específicos constantes.
Resolución
Proceso 1-2 compresión isentrópica
A partir del primer principio de la termodinámica para flujo
estacionario y despreciando los cambios de energía cinética y
energía potencial el trabajo del compresor esta dado por
 -W
  H entalpia  K cinetica  Potencial
Q
 comp  m
W
 h2  m
 h1
Ya que según la ecuación de continuidad para flujo permanente
m
2  m
1  m

Para calores específicos constantes, el trabajo del compresor de flujo másico
Wcomp  m (h2  h1 )
 p (T2  T1 )
Wcomp  mC
wcomp 
Wcomp
m
 C p (T2  T1 )
Dado que la compresión es isentrópica
T2  P2 
 
T1  P1 
( k 1) / k
 rp 
( k 1) / k
T2  T1 rp 
( k 1) / k
T2  2936
(1.4 1) / 1.4
 492.5K
Finalmente el trabajo del compresor será
wcomp  c p (T2  T1 )  1.005(492.5  295)
wcomp  198.15
kJ
kg
Proceso 3-4 expansión isentrópica
De la primera ley de la termodinámica para la turbina, para calores específicos constantes, se obtiene el siguiente resultado
Wturb  m (h3  h4 )
 p (T3  T4 )
Wturb  mC
wturb 
Wturb
 C p (T3  T4 )
m
Dado que la expansión es isentrópica.
Ciclos de Turbinas a Gas
Página | 10
Apuntes de Clase
Docente: Emilio Rivera Chávez
Como P3 = P2 y P4 = P1, vemos que
T4  P4 
 
T3  P3 
( k 1) / k
1
T4  T3 
r
 p




P 
  1 
 P2 
( k 1) / k
( k 1) / k
1
 1100 
6
1

r
 p




( k 1) / k
(1.4 1) / 1.4
 659.1K
En consecuencia el trabajo de la turbina es
wturb  c p (T3  T4 )  1.005(1100  659.1)
wturb  442.5
kJ
kg
Proceso 2-3 Adición de Calor a presión constante
El calor suministrado al ciclo por unidad de flujo másico proceso, para flujo permanente,
esta dado por (primera ley de la termodinámica)
Q a  m (h3  h2 )
Q
qa  a  h3  h2
m
Para calores específicos constantes
qa  c p (T3  T2 )
finalmente
qa  1.005(1100  492.5)
qa  609.6
kJ
kg
Por otra parte el trabajo neto realizado por el ciclo es
wneto  wturb  wcomp
wneto  442.5  198.15
wneto  244.3
kJ
kg
La eficiencia del ciclo se obtiene de
t ciclo  wq
neto
t ciclo 
a
244.3
 0.40
609.6
La relación de trabajo de retroceso se define como la fracción del trabajo de la turbina
que se emplea para accionar el compresor.
wtu rb 198.15

 0.448
wco mp 442.5
Ciclos de Turbinas a Gas
Página | 11
Apuntes de Clase
Docente: Emilio Rivera Chávez
Ejemplo 4
Una central eléctrica de turbina de gas estacionaria opera en un ciclo Brayton ideal simple con aire como
fluido de trabajo. El aire entra al compresor a 95 kPa y 290 K, mientras que a la turbina lo hace a 760 kPa
y 1100 K. Se transfiere calor hacia el aire a una tasa de 35000 kJ/s. Determine la potencia entregada por
esta central a) suponiendo calores específicos constantes a temperatura ambiente y b) considerando la
variación de los calores específicos con la temperatura.
Resolución
Hipótesis: de trabajo:
Condiciones de operación estacionaria,
Aire estándar como fluido de trabajo,
Aire como gas ideal.
Energía cinética y potencial despreciable.
a) Calculamos la potencia desarrollada por la central asumiendo calores específicos constantes.
El trabajo neto desarrollado por la central se puede calcular a partir del calor añadido y
del rendimiento térmico del ciclo.
Wn = ƞcicloQA
El rendimiento se puede calcular a partir de:
 ciclo  1 
QR
QA
y para calores específicos constantes
 ciclo  1 
c p (T4  T1 )
qR
T T
 1
 1 4 1
qA
c p (T3  T2 )
T3  T2
las temperaturas t4 y t2 se calculan a partir de los procesos de compresión y expansión
isentrópicos
p 
T2  T1  2 
 p1 
p 
T4  T3  4 
 p3 
 ciclo  1 
k 1
k
k 1
k
 760 
 290

 95 
1.41
1.4
 95 
 1100

 760 
1.4 1
1.4
 525.3K
 607.2 K
T4  T1
607.2  290
 1
 0.448
T3  T2
1100  525.3
finalmente
Wn = ƞcicloQA
wn  0.448  35000  15680kW
Ciclos de Turbinas a Gas
Página | 12
Apuntes de Clase
Docente: Emilio Rivera Chávez
b) Para calcular el trabajo neto considerando la variación de los calores específicos con la
temperatura., procedemos de la misma forma que en el inciso anterior, salvo que el rendimiento se calculará a partir de las entalpias las mismas que obtendremos a partir de tablas de aire como gas ideal.
Para T1=290 K  h1=290.1 kJ/kg; Pr1 = 1.2311
Con Pr1, p1 y p2, calculamos Pr2
Pr 2  Pr1
p2
760
 1.2311
 9.8488
p1
95
Para Pr2 = 0.8488  h2 = 526.12 kJ/kg
Para T3=1100K  h3 = 1161.07 kJ/kg; Pr3 = 167.1
Con Pr3, p4 y p3, calculamos Pr2
Pr 4  Pr 3
p4
95
 167.1
 20.89
p3
760
Para Pr4 = 20.89  h4 = 651.37 kJ/kg
Con las entalpias calculamos ahora el rendimiento térmico del ciclo,
 ciclo  1 
qR
h h
651.37  290.16
 1 4 1  1
 0.431
qA
h3  h2
1161.07  526.11
Entonces el trabajo neto sera,
Wn = ƞcicloQA
wn  0.431 35000  15085kW
Ciclos de Turbinas a Gas
Página | 13
Apuntes de Clase
Docente: Emilio Rivera Chávez
Variantes
La eficacia de un motor de Brayton puede ser
mejorada de las maneras siguientes:

Ínterenfriador (fig. 2a), el fluido de
trabajo luego de pasar a través de una primera
etapa de compresión, pasa por un ínter enfriador
y una segunda etapa de compresión antes ingresar a la cámara de combustión. Si bien esto
requiere un aumento en el consumo de combustible en la cámara de combustión, permite una
reducción del calor específico del fluido que
ingresa a la segunda etapa de compresión, con
una consiguiente disminución de la cantidad
total de trabajo necesitado para el proceso de
compresión. Recalentamiento (fig2b), el fluido
de trabajo - generalmente aire- se expande a
través una serie de turbinas, luego pasa a través
de una segunda cámara de combustión antes de
expandirse a la presión ambiente a través de un
sistema final de turbinas. Esto tiene la ventaja de
aumentar la energía posible de salida para una
determinada relación de presión sin exceder
ninguna restricción metalúrgica.


Regeneración (fig. 2c), los gases calientes
que salen de la turbina pasan por un intercambiador de calor para precalentar el fluido
que ingresa a la cámara de combustión. Esto permite un menor consumo de combustible y menores perdidas de energía por calor
no utilizado.
Los sistemas de cogeneración, hacen uso
del calor desechado en las máquinas de
Brayton, típicamente para la producción de
agua caliente o la calefacción.
Ciclos de Turbinas a Gas
Applications
The efficiency of a Brayton engine can be
improved in the following manners:

Intercooling (fig. 2a), wherein the working
fluid passes through a first stage of
compressors, then a cooler, then a second
stage of compressors before entering the
combustion chamber. While this requires an
increase in the fuel consumption of the
combustion chamber, this allows for a
reduction in the specific heat of the fluid
entering the second stage of compressors,
with an attendant decrease in the amount of
work needed for the compression stage
overall. Reheat (fig. 2b), wherein the
working fluid—in most cases air—expands
through a series of turbines, then is passed
through a second combustion chamber
before expanding to ambient pressure
through a final set of turbines. This has the
advantage of increasing the power output
possible for a given compression ratio without exceeding any metallurgical constraints.

Regeneration (fig. 2c), wherein the stillwarm post-turbine fluid is passed through a
heat exchanger to pre-heat the fluid just
entering the combustion chamber. This
allows for lower fuel consumption and less
power lost to waste heat.

Cogeneration systems make use of the
waste heat from Brayton engines, typically
for hot water production or heating.
Página | 14
Apuntes de Clase
Docente: Emilio Rivera Chávez
FIGURA 6.-Variantes de las Turbinas a Gas
Fuel
Combustor
T
5
6r
Comp.
II
Comp.
I
Turb.
6
2r
4r
2
4
1
3
s
Intercooler.
Fig. 6a GAS TURBINE WITH INTERCOOLING
T
More Fuel
Fuel
Combustor
3
5
6r
Reheater.
4
r
6
4
2r
2
Comp.
Turb.
I
Turb
II
1
s
Fig. 6b GAS-TURBINE WITH REHEATER
Regenerator.
3
Fuel
Combustor
4r
5
7
4
2r
Comp.
II
Turb.
I
2
8
6
1
s
Fig. 6c GAS-TURBINE WITH REGENERATION
Ciclos de Turbinas a Gas
Página | 15
Apuntes de Clase
Docente: Emilio Rivera Chávez
Otras maneras de mejorar la eficiencia
del ciclo Brayton
Other Ways to Improve Brayton Cycle
Performance
El Interenfriamiento y recalentamiento son dos
maneras importantes para mejorar el rendimiento del ciclo de la Brayton con regeneración
Intercooling and reheating are two important
ways to improve the performance of the Brayton
cycle with regeneration
Regenerator.
Fuel
Com-
bustor
Comp.
II
Comp. I
Turb.
I
More Fuel
Recalentador
Turb
II
Intercooler
Ciclos de Turbinas a Gas
Página | 16
Apuntes de Clase
Docente: Emilio Rivera Chávez
Turbina de Gas sencilla con un compresor y turbina reales. (Efectos de la Fricción del Fluido).
El ciclo real sencillo de potencia de una turbina de gas es muy sensible a las irreversibilidades del compresor y de la turbina, resulta por tanto importante estudiar el efecto que tiene sobre el ciclo la compresión y expansión irreversibles en un turbina de gas real.
T
3
qA
Qa
2
r
2
4r
4
qR
1
S
A partir del diagrama de energía, T-s, se tiene, al suponer un gas ideal con calores específicos constantes, los siguientes trabajos de fluido:
WT= h3-h4=cp(T3-T4r)
;
WC= h1-h2r=cp(T1-T2r)
De la definición de eficiencia de la turbina, se tiene:
T 
h3  h4 r

h3  h4
T3  T4 r
T3  T4
C 
h2 R  h1
h2  h1
T2 R  T1

T2  T1
A partir de estas ecuaciones se puede escribir también ecuaciones para el trabajo:

1 
wT  T c pT3 1  (k 1) / k  ;
 rp

wC  
c pT1
C
r
(k 1) / k
p

1
Entonces el trabajo neto desarrollado durante el ciclo, esta dado por:
wneto  c p (T3  T4r )  c p (T2r  T1 )
Ecuación que luego de algunas operaciones puede escribirse del siguiente modo,



1  c pT1 (k 1) / k
wneto  T c pT3 1  (k 1) / k  
rp
1
 rp
 C
La razón de presiones optima, para un trabajo máximo esta dada por:
Ciclos de Turbinas a Gas
Página | 17
Apuntes de Clase
Docente: Emilio Rivera Chávez
r popt
T

  3  T  C 
 T1

k / 2(k 1)
El calor añadido durante el ciclo es:
Qent = Q23r cp(T3r-T2)
Qent


(k 1) / k


rp
 1 



 c p T3  T1 1 
C

 



Finalmente, la eficiencia térmica del ciclo está dada por:
t 
T
t
T3
T1
wneto
Qent



1  1 (k 1)/ k
rp
1
1  (k 1)/ k  
 rp
 C
( k 1)/ k
 1
T3  rp
 1 

T1 
C

Ejemplo 5:
o
En un ciclo estándar de aire para turbina de gas, en el estado 1, p1=1.0 Bar abs. y t1=15 C , la relación de
o
presión es 6. La temperatura máxima del ciclo es 780 C. el rendimiento de la turbina es 82% y el del
compresor es 82% ¿Qué disminución en la eficiencia de la turbina producirá el mismo efecto en el rendimiento del ciclo, que una disminución en la del compresor hasta 75%, si los demás valores permanecen
inalterados?
RESOLUCIÓN
1.- Calculamos en primer lugar la eficiencia del sistema (ciclo) con los datos de diseño, es
o
decir: Tmin=15 C, Tmax=780, T=82%, c=82% y rp=6.
Para esto empleamos la conocida relación:
t 
wneto
qA
Donde:
W neto = W T- W C

1 
wT  T c pT3 1  (k 1) / k 
 rp

wC  
y

c pT1
C
r
(k 1) / k
p

1

( k 1) / k


rp
1 


q A  c p T3  T1 1 

C


 


Ciclos de Turbinas a Gas
Página | 18
Apuntes de Clase
Docente: Emilio Rivera Chávez
2. Luego calculamos el efecto de la disminución del rendimiento del compresor en el rendimiento del sistema (ciclo). Es decir que repetimos los cálculos anteriores sustituyendo el
rendimiento del compresor por: c=75%. Y mantenemos el resto de los datos constantes.
3. Finalmente con el rendimiento del sistema calculado en el paso 2, calculamos ahora la
disminución del rendimiento de la turbina que provocaría el mismo efecto sobre el rendimiento del sistema, provocado por la disminución del rendimiento del compresor.
Se mantiene el rendimiento del compresor en 82%. Para este propósito se puede usar la siguiente relación:
T
t(sist) 
T3
T1



1  1 (k 1) / k
rp
1
1  (k 1) / k  
 rp
 C
( k 1) / k
 1
T3  rp
 1 

T1 
C

De la que se despeja el rendimiento de la turbina.
El la siguiente hoja se presenta un resumen de los datos y cálculos realizados en una planilla electrónica.
Resumen de datos
Tmin
Tmax
p1
p2
rp
rend. Turb
rend. comp
Cp
k
15.00
780.00
100.00
?
6.00
77.72
82.00
1.0038
1.40
288.00
1053.00
100.00
600
6.00
0.7772
0.82
Ciclos de Turbinas a Gas
rend.
Turb.
rend.
Comp.
Tabla de resultados
Trabajo Traba- Calor
Rend
Com.
jo Turb entrada Ciclo
1
82
82
235.69
347.27
532.22
20.97
2
82
75
257.68
347.27
510.22
17.56
3
77.72
82
235.69
329.15
532.22
17.56
Se observa que el rendimiento del sistema se
ve
afectado en mayor grado por el rendimiento de
la turbina.
Página | 19
Apuntes de Clase
Docente: Emilio Rivera Chávez
Ejemplo 6.
En el compresor de un motor de turbina de gas entra aire a 300 K y 100 kPa, en el que se comprime
hasta 700 kPa y 580 K. El calor se transfiere hacia el aire en la cantidad de 950 kJ/Kg antes de entrar a la
turbina. Para una eficiencia de la turbina de 86% determine a) la fracción de la salida de trabajo de la
turbina utilizada para accionar el compresor y b) la eficiencia térmica. Suponga calores específicos variables para el aire.
a) Calculamos primero los trabajos del compresor y la turbina:
3
T
wc  h2 r  h1
qA
T1=300K  h1 = 300.19 kJ/kg
T2 = 580K  h2r = 586.04 kJ/kg
2r
4r
2
Wc = 586.04 – 300.19 = 285.85 kJ/kg
4
qR
1
S
En el caso de la turbina, calculamos el trabajo a partir
de las entalpias isentrópicas y del rendimiento térmico
de la turbina
wt   t h3  h4 
h3 se puede calcular a partir de calor añadido,
qA = h3 – h2  h3 = qA + h2 = 950 + 586.04 = 1536.04 kJ/kg
para h3 = 1536.04 kJ/kg  Pr3 = 474.11
Calculamos ahora Pr4 ;
Pr 4  Pr 3
p4
100
 474.11
 67.73
p3
700
para Pr4 = 67.73  h4 = 905.83 kJ/kg
WT= ƞ(h3- h4) = 0.86(1536.04-905.83) = 542.0 kJ/kg
Finalmente:
wc 285.85

 0.527
wt
542.0
b) El rendimiento se puede calcular a partir de:
 ciclo 
 ciclo 
Ciclos de Turbinas a Gas
wneto wT  wC


qA
qA
542.0  285.85
 0.270
950
Página | 20
Apuntes de Clase
Docente: Emilio Rivera Chávez
El Ciclo de Brayton con recuperación (regeneración)
Como ya se menciono anteriormente, es posible mejorar la eficiencia del ciclo Brayton simple precalentando el aire que sale del compresor antes de que ingrese a la cámara de combustión con los gases
calientes que salen de la turbina (gas de escape), lo que permite un menor consumo de combustible.
En la siguiente figura se muestra un ciclo de Brayton con recuperación perfecta, es decir que idealmente
el calor absorbido por el aire que sale del compresor es igual al calor que ceden los gases de escape de
la turbina.
Ciclo de Brayton con recuperación perfecta
T
3
5
Recuperador
6
5
4
Cámara de
Combustión
1
2
6
2
T
C
1
4
3
s
Para este ciclo el trabajo esta dado por:
wneto  c p (T3  T4 )  c p (T2  T1 )
Qent = Q53 =cp(T3-T5)
y
Pero además para el caso de recuperación perfecta (ideal), : T 5 = T4 y por tanto:
Qent = Q53 =cp(T3-T4)
En consecuencia la eficiencia del ciclo está dada por:
t 
c p (T3  T4 )  c p (T2  T1 )
c p (T3  T4 )

(T3  T4 )  (T2  T1 )
(T3  T4 )
Reordenando adecuadamente tenemos
T
T1( 2  1)
(T  T )
T1
t  1  2 1  1 
T
(T3  T4 )
T3(1  4 )
T3
Ciclos de Turbinas a Gas
Página | 21
Apuntes de Clase
Docente: Emilio Rivera Chávez


 p2 

T1    1
 p1 



t  1 
k 1


 p4  k 

T3 1   


 p3  


k 1
k
Además p2=p3 y p1=p4, por lo que la ecuación anterior resulta:
k 1
k 1




 p2  k
 p2  k







T1    1
T1    1
 p1 

 p1 







t  1 
1
k 1
k 1
k 1





p k
p  k p k
T3 1   1  
T3  2   2   1
  p2  

 p1   p1 




Finalmente:
t  1 
T1  p2 
 
T3  p1 
k 1
k
 1
k 1
T1

rp  k
T3
Ejemplo 7: Un ciclo de aire estándar de Brayton con regeneración perfecta, opera entre los límites de
o
temperatura de 1600 y 80 F. Calcúlese le eficiencia térmica del ciclo para las siguientes razones de presión: 2, 4, 6, 8, 10, y 12. Grafíquese la eficiencia térmica contra la razón de presiones:
RESOLUCIÓN
Con la ecuación deducida anteriormente
t  1 
k 1
T1
rp  k
T3
Calculamos el rendimiento térmico para cada relación de presión y cuyos resultados
numéricos y gráfico se resumen a continuación.

68.0452731
61.0467516
56.2623477
52.5154584
49.389477
46.6832046
Rendimiento termico vs. relación de presión
80
rendimiento térmico
rp
2
4
6
8
10
12
70
60
50
Serie1
40
30
20
0
5
10
15
relación de presión
Ciclos de Turbinas a Gas
Página | 22
Apuntes de Clase
Docente: Emilio Rivera Chávez
En la práctica no es posible obtener una recuperación perfecta, lo cual se traduce en que la temperatura
del aire que entra a la cámara de combustión es menor que la temperatura de los gases de escape de la
turbina.
T
3
7
5
7
4
2
Cámara de
Combustión
1
2
8
6
1
Recuperador
8
4
3
T
C
s
Se define como efectividad de un recuperador a la relación:
 rec 
h7  h2
h4  h2
De donde para calores específicos constantes, se tiene:
 rec 
T7  T2
T4  T2
Ejemplo 8
Un ciclo Brayton ideal con regeneración tiene una relación de presiones de 10. El aire entra al compresor
a 300 K mientras que a la turbina lo hace a 1150 K. Si la eficacia de regenerador es de 100%, determine
la salida neta de trabajo y la eficiencia térmica del ciclo. Considere calores específicos constantes a temperatura ambiente.
Como ƞrec = 1, entonces, indudablemente, se trata de un ciclo ideal Brayton con regeneración
T
Recuperador
6
3
5
5
Cámara de
Combustión
4
2
1
2
6
4
3
C
1
T
s
DATOS: T1=300 K; T3=1200 K; cp =1.005 kJ/kg
el trabajo neto se calcula a partir de;
wneto  wturb  wcomp
cp  cte
wneto  (h3  h4 )  (h2  h1 )  cp(T3  T4 )  (T2  T1 )
Ciclos de Turbinas a Gas
Página | 23
Apuntes de Clase
Docente: Emilio Rivera Chávez
las temperaturas T2 y T4, se calculan a partir de los procesos isentrópicos de compresión 1-2 y
expansión 3-4 (ya que se trata de un ciclo ideal).
proceso 1-2:
T2  T1rp
T4  T3rp
proceso 3-4:
( k 1) / k
 300rp
 ( k 1) / k
0.4 / 1.4
 579.2
 120010
0.4 / 1.4
 621.5
wneto  1.005(1200  621.5)  (579.2  300)
luego,
wneto  300.8kJ / kg
finalmente, la eficiencia del ciclo se calcula a partir de la definición,
 ciclo 
wneto
wneto

qA
c p (T3  T5 )
regenerador ideal  T5  T4
300.8
 0.5175
1.005(1200  621.59)
 51.75%
 ciclo 
 ciclo
Ejemplo 9
Un ciclo Brayton ideal con regeneración que emplea aire como fluido de trabajo tiene una relación de
presiones de 7. Las temperaturas mínima y máxima del ciclo son 310 y 1200 K. Suponga una eficiencia
isentrópica de 75% para el compresor y 82% para la turbina, así como una eficacia de 65% para el regenerador, determine a) la temperatura del aire a la salida de la turbina b) la salida neta de trabajo c) la
eficiencia térmica.
T
3
8
Recuperador
7
4r
5
7
2
Cámara de
Combustión
4
2r
8
1
6
1
2
C
s
4
3
T
DATOS: T1=310 K; T3=1150 K; rp =7; ƞturb=0.82; ƞcomp=0.75; ƞreg=0.65
Para T1=310 K h1=310.24 kJ/kg; Pr1=1.5546
a) con Pr1=1.5546 y rp calculamos Pr2;
Con Pr2=10.88  h2=310.24 kJ/kg
p 
Pr 2  Pr1  2   1.5546  7  10.88
 p1 
(entalpia isentrópica)
A partir del rendimiento del compresor podemos calcular la entalpia real h2r ;
Ciclos de Turbinas a Gas
Página | 24
Apuntes de Clase
Docente: Emilio Rivera Chávez
comp 
h2  h1
h h
541.26  310.24
 h2 r  h1  2 1  310.24 
 618.26kJ / kg
h2 r  h1
C
0.75
con T3=1150 K h3=1219.25 kJ/kg; Pr3=200.15
con Pr3=200.15 y rp calculamos Pr4;
para Pr4=28.59  h4=711.80 kJ/kg
p 
Pr 4  Pr 3  4   200.15 / 7  28.59
 p3 
(entalpia isentrópica)
A partir del rendimiento de la turbina podemos calcular la entalpia real h4r ;
turb 
h3  h4 r
 h4 r  h3  turbh3  h4   1219.25  0.82(1219.25  711.8)  803.14kJ / kg
h3  h4
entonces T4r =782.8 K
b)
wneto  wturb  wcomp
wneto  (h3  h4 r )  (h2 r  h1 )  (1219.25  803.14)  (618.26  310.24)
wneto  108.1kJ / kg
c)
 ciclo 
reg 
luego,
wneto
w
 neto
qA
h3  h7
h7  h2 r
 h7  h2 r  reg h4  h2 r   618.26  0.65(803.14  618.26)  738.43kJ / kg
h4  h2 r
 ciclo 
wneto
108.1

 0.225
h3  h7 1219.25  738.43
 ciclo  22.5%
Ciclos de Turbinas a Gas
Página | 25
Apuntes de Clase
Docente: Emilio Rivera Chávez
Efecto de la caída de presión en el proceso de intercambio de calor.
Ya se vio anteriormente el efecto nocivo de las irreversibilidades en la eficiencia tanto del compresor
como de la turbina lo que repercute sensiblemente en la eficiencia del ciclo. Otro factor que también afecta la eficiencia de los sistemas de ciclo cerrado, es la caída de presión en los intercambiadores de calor
1
(cámara de combustión) . En este epígrafe estudiará el efecto de la caída de presión en la eficiencia de
los sistemas de generación de ciclo cerrado con turbina y compresor reales.
En el diagrama T-s, se representa estas condiciones en el ciclo, disminuyendo en consecuencia la eficiencia del ciclo.
T
qA
3r
4r
2r
4
2
qR
1
S
El trabajo de compresión esta dado (gas ideal y Cp=cte.) por la ecuación:
wC  
r
c pT1
C
r
(k 1) / k
p

1
r
La relación de presiones en la turbina, p3 /p4 , denominada también como razón de expansión se puede
expresar en términos de la razón de compresión rp. y de las caídas de presión que ocurren en cada uno
de los procesos de intercambio de calor. Las presiones de entrada y salida de cada intercambiador se
pueden relacionar a través del llamado factor de caída de presión (que no es más que la razón entre
ambas presiones), así con referencia a la figura se tiene:
Para el intercambiador en el se añade calor al gas, proceso 2-3.
p3r=23p2r
y para el intercambiador de calor en el que se realiza el rechazo de calor.
p1r=41p4r
Combinando estas ecuaciones se tiene que la relación de expansión, esta dada por:
1
El proceso de compresión para elevar la presión en el ciclo Brayton requiere un mayor consumo de energía y gran parte del trabajo producido
por la turbina es consumido por el compresor, en un porcentaje que puede estar entre 40% y 80%. Esta desventaja hace necesario prestar una
mayor atención en el diseño de turbinas de gas ya que cualquier pérdida de presión en la cámara de combustión y demás componentes entre
el compresor y la turbina debe compensarse con mayor trabajo en el compresor. Adicionalmente, la eficiencia del compresor y la turbina juegan
un papel muy importante, debido a que eficiencias cercanas al 60% en estos componentes ocasionarían que todo el trabajo producido por la
turbina sea consumido por el compresor y por tanto la eficiencia global sería cero
Ciclos de Turbinas a Gas
Página | 26
Apuntes de Clase
Docente: Emilio Rivera Chávez
p 3r
p 4r
pr
  23  41  2    23  41 rp 
 p1 
Entonces el trabajo de la turbina estará dado por:
WT  c p (T3r  T4r )
Y recordando que el rendimiento de la turbina es:
T 
T3r  T4r
T3r  T4
Se tiene

T
WT  c pT (T3r  T4 )  c p T T3r 1  4
 Tr
3





r
Como el proceso 3 -4 es isentrópico:
pr
  3 
T4  p 4 
T3r
k /( k 1)
r
Además p4=p4 , entonces:
pr 
 3 
T4  p 4r 
T3r
k /( k 1)
  23  41rp 
k /( k 1
Finalmente


1
wT  T c pT3r 1 

(k 1)/ k




r


23 41 p
El trabajo neto se puede calcular entonces con la siguiente relación:



 c pT1 (k 1)/ k
1
wneto  T c pT3r 1 
rp
1

(k 1)/ k
  23 41rp 
  C
La potencia especifica desarrollada por el ciclo esta dada por


 1 (k 1)/ k
Tr 
wneto
1
 T 3 1 
rp
1

c pT1
T1   23 41rp (k 1)/ k   C


Ciclos de Turbinas a Gas
Página | 27
Apuntes de Clase
Docente: Emilio Rivera Chávez
Razón de presiones optima para maximizar la potencia específica del ciclo.
Para un conjunto dado de valores de las temperaturas máxima y mínima del ciclo así como de los rendimientos de la turbina y del compresor además de las propiedades del gas, existe un valor optimo para la
razón de presiones rp que permite maximizar la potencia especifica del ciclo, este valor se obtiene a partir
de la ecuación anterior y esta dado por:
k
rp opt. 
1
 23 41
 T3r
 2(k 1)
 T C 
 T1

Calor agregado
El calor agregado al gas durante el ciclo viene dado por la ecuación:
qent=q2r3r =cp(T3r-T2r)
a partir de la que se obtiene la siguiente expresión:
qent


( k 1) / k


rp
 1 


 c p T3  T1 1 

C


 


Eficiencia térmica
Como se sabe la eficiencia térmica del ciclo, esta dada por:
t 
Wneto
Qent
en la que sustituyendo las expresiones para el trabajo neto, Wn y calor entregado, Qent, se obtiene:


 1 (k 1)/ k
T3r 
1
T
rp
1
1 

T1   23 41rp (k 1)/ k   C


t 
(k 1)/ k
T3r 
rp
1 
 1 

T1 


C



Razón de presiones optima para maximizar la eficiencia térmica del ciclo.
Como en el caso anterior, para un conjunto de valores de los rendimientos de la turbina y del compresor,
además de las propiedades del gas y una relación de temperaturas máxima-mínima, T3/T1, existirá un
valor optimo para la razón de presiones rp que permite maximizar la eficiencia térmica del ciclo, este
valor se obtiene derivando loa ecuación anterior respecto de r p e igualando esta derivada a cero. El resultado es el siguiente:
2
a(rp) - brp + c = 0
k
rp opt.
Ciclos de Turbinas a Gas
 b  b 2  4ac  (k 1)


2a


Página | 28
Apuntes de Clase
Docente: Emilio Rivera Chávez
donde
a
T3 T T3 / T1  1

T1 C
C
b
c
2T T3
 C T1
T
k 1
k
 23 41
 1 
  
 23 41 
k 1
k
T3  T3r
1

1
T1  T1
C



Tanto el trabajo neto de la turbina así como la eficiencia del ciclo, alcanzan un valor máximo para una
determinada relación de presión rp,opt, Ahora la relación de presiones optima difiere de en cada caso.
En el diagrama se muestra la evolución tanto del trabajo neto como de la eficiencia del ciclo al aumentar
la relación de presión. En este caso el trabajo neto alcanza un valor máximo para rp opt. de 7 mientras que
para maximizar la eficiencia se requiere una rpopt. de 15.
Otro aspecto a resaltar en este diagrama es que la variación del trabajo neto es más sensible a una variación de la relación de presión.
Tmin
Tmax
rp
rend. Turb
rend. comp
caida presión
β12
β41
cp
k
303
1123
15.5
90%
90%
3%
1.0450
1.4
K
K
0.9
0.9
0.03
0.97
0.97
kJ/kg-K
rpopt
Trabajo Compresor
Trabajo Turbina
Trabajo neto
Calor entrada
ƞ Ciclo
Wc/Wt
15.50
407.28
558.23
150.96
449.62
33.57%
0.73
Ciclos de Turbinas a Gas
Página | 29
Apuntes de Clase
Docente: Emilio Rivera Chávez
Efecto de la caída de presión en el proceso de intercambio de calor en sistemas
con recuperación.
T
3r
qA
4r
4
2r
7
8
2
qR
1
S
En esta sección se estudia la situación en la que presentan simultáneamente las dos efectos estudiados
en las clases anteriores, es decir es decir el efecto de un regenerador, las irreversibilidades en el compresor, turbina y regenerador, así como la caída de presión en los intercambiadores de calor, sobre la
eficiencia térmica del ciclo. El diagrama Ts de este sistema se muestra en la figura.
Un análisis similar al realizado en la sección anterior nos permite resumir las siguientes ecuaciones para
el calculo de los trabajos del compresor y la turbina, el trabajo neto y el calor añadido en la cámara de
combustión, en base a cuyos valores se puede estimar la eficiencia térmica del ciclo.
Trabajo del compresor:
wC  
c pT1
C
r
(k 1) / k
p

1
Trabajo de la turbina:


1
wT  T c pT3r 1 

(k 1)/ k
  27  73 48rp 

Donde:
27; es el factor de caída de presión en el lado frió del regenerador,
73; es el factor de caída de presión en el calentador de aire.
48; es el factor de caída de presión en el lado caliente del regenerador.
Trabajo Neto



 c pT1 (k 1)/ k
1
wneto  T c pT3r 1 
rp
1

(k 1)/ k






r


C
27 73 48 p
Trabajo específico:


 1 (k 1)/ k
Tr 
wneto
1
 T 3 1 
rp
1

c pT1
T1   27  73 48rp (k 1)/ k   C


Ciclos de Turbinas a Gas
Página | 30
Apuntes de Clase
Docente: Emilio Rivera Chávez
Razón de presiones optima para maximizar la potencia especifica del ciclo.
k
rp opt. 
1
 27  73 48
 T3r
 2(k 1)
 T C 
 T1

Calor agregado
qent


( k 1) / k


rp
 1  
 c p T3  T1 1 

C


 



1

  rec c pT3 1  T 1 
    r ( k 1) / k

27 73 48 p



 r ( k 1) / k  1 
 c pT1 1  p
 


C

 

Razón de presiones optima para maximizar la eficiencia térmica del ciclo.
Para valores dados de temperaturas mínima y máxima y rendimientos de la turbina y del compresor y
factores de caída de presión, existirá un valor óptimo para la razón de presiones, que permita obtener una
máxima eficiencia térmica del ciclo. Expresión que se puede obtener a partir de la ecuación de rendimiento, de la que se obtiene por derivación la siguiente expresión:
 b  b  4ac 
rp opt.  

2a


2
k
( k 1)
Donde:


 T3'    T 
 1   rec    1  3'  T 2 rec  1


 T1     T1 
 27  73 48rp ( k 1) / k
a

C
C




T 
2 3'  T 1  2 rec 
T1
b  
C
 T3' 
  T 2 rec  1
 T 3' 
 T 3'   T1 
1  2 rec 1 

c   T 
T1 
C
 T1 

Ciclos de Turbinas a Gas
Página | 31
Apuntes de Clase
Docente: Emilio Rivera Chávez
El diagrama muestra el efecto del regenerador en la evolución del trabajo y la eficiencia térmica en función de la relación de presión.
En este caso el trabajo neto alcanza un valor máximo para rpopt. de aproximadamente 2.7, mientras que
para maximizar la eficiencia se requiere una rpopt. de 8.7.
Otro aspecto a resaltar en este diagrama es que la variación del trabajo neto es más sensible a una variación de la relación de presión (Se sugiere al estudiante, comparar este diagrama con el de la pagina
23).
Tmin
300 K
Tmax
1130 K
ƞ reg
90%
0.9
ƞTurb
90%
0.9
ƞ comp
90%
caida presión
3%
cp
0.9
0.03
1.045 kJ/kg-K
k
1.39
Ejemplo 10.
Se desea diseñar una central termoeléctrica de turbina de gas con recuperación, de acuerdo a las sio
o
guientes especificaciones: T max=857 C, Tmin=27 C, eficiencia adiabática del compresor 90%, eficiencia
adiabática de la turbina 90%, eficiencia del recuperador 90%, caída de presión en cada circuito de transferencia de calor 3%. Suponiendo que el aire es un gas ideal con calores específicos constantes de
1.0450 kJ/kg K y k=1.39, calcúlese la eficiencia térmica del ciclo para razones de presión 2, 4, 6, 8 y 10
¿Cuál es la razón de presiones para máxima eficiencia térmica?
T
3
r
qA
Recuperador
8
4
7
r
4
2r
C. C.
7
8
2
1
qR
2
r
C
4r
3
T
S
La eficiencia térmica del ciclo, está dada por:
 ciclo 
y el trabajo del compresor
wneto wturb  wcomp

qA
qA
(1)
cp  cte.
wcomp  h2 r  h1  wcomp  c p (T2 r  T1 ) (2)
Ciclos de Turbinas a Gas
Página | 32
Apuntes de Clase
Docente: Emilio Rivera Chávez
la temperatura real a la salida del compresor, se puede determinar a partir de rendimiento del compresor,
comp 
h2  h1 cp  cte.
T T
T T
T  300
 comp  2 1  T2 r  T1  2 1  300  2
(3)
h2 r  h1
T2 r  T1
C
0.9
La temperatura isentrópica T2, se calcula a partir de,
T2  T1rp
( k 1) / k
 300rp
0.39 / 1.39
(4)
Procedemos de manera similar para calcular el trabajo desarrollado por la turbina
cp  cte.
wturb  h3  h4 r  wturb  c p (T3  T4 r ) (5)
turb 
h3  h4 r cp  cte.
T T r
 turb  3 4  T4 r  T3  turb T3  T4 
h3  h4
T3  T4
T4 
La temperatura isentrópica T4
 T4 r  1130  0.9(1130 T 4)
(6)
T3
 p3 
 
 p4 
( k 1) / k
Calculamos ahora, la relación de presiones p3/p4, en función de p2/p1,
p3  p7  0.03 p7  0.97 p7  0.97( p2  0.03 p2 )  0.972 p2 ;
y
p1  p4  0.03 p4  0.97 p4
finalmente,
p3
p
 0.973 2
p4
p1
T4 
1130

p 
 0.973 2 
p1 

0.39 / 1.39
(7)
cp  cte.
El calor añadido, se calcula q A  h3  h7  q A  c p (T3  T7 ) (8)
La temperatura T7, a partir de la eficiencia del regenerador,
h7  h2 r cp  cte.
T T r
 reg  7 2  T7  T2 r  reg T4 r  T2 r  (9)
h4 r  h2 r
T4 r  T2 r
Aplicando estas nueve ecuaciones, sucesivamente, para las 6 relaciones de presión p2/p1 dadas, se obtienen los siguientes resultados:
reg 
rp
2
4
6
8
10
12
Wt
165.11
323.76
403.22
454.37
491.29
519.79
Wc
74.78
165.61
227.54
275.95
316.28
351.17
Wneto
90.33
158.14
175.69
178.42
175.01
168.62
qE
227.85
361.56
426.88
468.07
497.27
519.43
Ƞciclo
39.64%
43.74%
41.16%
38.12%
35.19%
32.46%
Wc/Wt
0.45
0.51
0.56
0.61
0.64
0.68
De esta tabla se ve que para rp=4 se obtiene la máxima eficiencia.
Ciclos de Turbinas a Gas
Página | 33
Apuntes de Clase
Docente: Emilio Rivera Chávez
Ejemplo 11.
Sale aire del compresor de una turbina de gas y penetra en el combustor a 482.64 kPa abs.,
204.4OC y 45 m/s; los gases salen de este último a 468.85 kPa abs., 893.3oC y 152 m/s. Entra
combustible líquido a 15.60C con poder calorífico de 42920 kJ/kg; la eficacia del combustor es
94%. Calcule el flujo de combustible por kilogramo de aire entrante. Para los productos,
Mp=28.9, k=1.36.
RESOLUCIÓN
A continuación se exponen los pasos a seguir para la solución del problema sin tomar en
cuenta dos factores: El incremento de energía cinética y la caída de presión en el combustor. El estudiante se encargará de hacer las correcciones correspondientes explicando en
base a los resultados numéricos la incidencia de estos factores en los resultados finales.
T
mcomb
Qent
2
3
c-comb=94%
maire
3
mprod.
m prod  maire  mcomb
2
S
El calor añadido en el combustor se puede evaluar de la siguiente manera:
qi mcombccomb  m prodc p 2T2  mairec p1T1
qi
m
m  m prod
mcomb
m
 ccomb  prod c p 3T3  aire c p 2T2  aire
c p 3T3  c p 2T2
maire
maire
maire
maire
qi ccomb rc / a  (1  rc / a )c p3T3  c p 2T2
De donde se tiene una relación matemática que permite calcular la relación de flujo de combustible
– aire:
ra / c 
c p 3T3  c p 2T2
qi ccomb  c p 3T3 2
el calor específico del aire se obtiene de tablas y para calcular el calor específico de los gases producto
de la combustión se puede usar la siguiente relación termodinámica:
cp 
Ciclos de Turbinas a Gas
kR
; donde R=RU/Mp
k 1
Página | 34
Apuntes de Clase
Docente: Emilio Rivera Chávez
Ejemplo 12
De una turbina de gas industrial de 5150 kW se conocen los datos siguientes: Es de ciclo regenerativo;
temperatura de admisión 15ºC ; presión de admisión 1 atm; temperatura de entrada a la turbina 955ºC;
relación de compresión del compresor 8/1; rendimiento del compresor 0,85; rendimiento turbina: 0,88;
rendimiento cámara combustión: 0,96; rendimiento mecánico de la instalación: 0,98; pérdida de presión al
atravesar el fluido el regenerador: 2,5%: pérdida de presión en la cámara de combustión: 3%; pérdida de
presión en el escape: 2,5%. Potencia calorífica inferior del combustible: 42000 kJ/kg.
Determinar el ciclo, estimando los parámetros no conocidos, y calcular el rendimiento, y el gasto de aire.
Asumir que cp = 1 kJ/kgºC y k = 1,4.
RESOLUCIÓN
DA TOS: ( Mathcad )
P  5150
T  15  273
1
c  85%
Kw
t  88%
K
cc  96%
T  955  273 K
3
prg  2.5%
27  1  prg
27  0.975
pcc  3%
73  1  pcc
73  0.97
pesc  2.5%
48  1  pesc
48  0.975
mec  98%
rp  8
kJ
qi  42000
k  1.4
kg
cp  1
kJ
kgC
Ecuaciones para el cálculo de los trabajos
del compresor y la turbina
Diagrama T -s
wC 
c pT1
C
r
( k 1)/ k
p

1


1

wT   T c p T3r 1 
( k 1)/ k
  27  73  48rp 

- Calculamos primero la dosificación combustible aire, a partir del calor añadido en el combustor,
uitlizando la ecuación para el caso de una turbina con un ciclo con regeneración y caidas de presión en
los intercambiadores (no se tomará en cuenta el e fecto diluyente del combustible)::





 rp(k 1)/ k 1 


 rp(k 1)/ k 1
1



 c T 1
 reg c pT3r 1 T 1 

qent  c p T3r  T1 1
    r (k 1)/ k  p 1 
C





C


27
73
48
p








suponiendo un rendimiento térmico del regenerador de :
reg  100%
, se tiene:
qe  470.095
kJ
kg
ademas, el calor añadido se puede calcular a partir del poder calorifico del combustible y del gasto de
combustible:
q ent maire comb  qi mcomb cc
q ent (1  rc / a )  qi rc / a cc
Ciclos de Turbinas a Gas
Página | 35
Apuntes de Clase
Docente: Emilio Rivera Chávez
de donde se puede calcular la dosificación combustible aire:
rc / a 
qent
qi cc  q ent
rca  0.012
Cálculo del trabajo desa rrollado por el compresor:
cp  T
Wc 
c
1
 k 1 
 k

  rp
 1
Wc  274.937
Cálculo del trabajo desa rrollado por la turbina:
Wt  t cp  T   1 
3




1
k 1 
 27 73 48 rp
k


Wt  470.095
Wneto  Wt  Wc
TRabajo neto (util)
Wneto  195.157
Gasto de aire:
KJ
kg
P  Wneto mec  wneto  maire  mec
m aire 
maire 
 sistema 
P
w neto  mec
P
Wneto  mec
 26.928
kgaire
s
mcomb 
26.9280.012

 0.323
P
P
Qañadido

mcomb qi
 sistema 
P
mcomb qi
 0.386 ( 38.6%)
¿Si se toma en cuenta e l efecto de dilución del combustible, como y en q ue magintud afectará al
rendimiento del sistema?
Ciclos de Turbinas a Gas
Página | 36
Apuntes de Clase
Docente: Emilio Rivera Chávez
TURBOPROPULSORES (TURBINAS) VS. TURBORREACTORES (MOTORES A REACCION)
Diagramas P-V y T-S del ciclo idealizado:
No existe mayor diferencia entre los dos casos, en el ciclo termodinámico, por lo que en ambos casos los diagramas
P-v y T-s, son idénticos.
Diagrama de Bloques:
(a) Turbopropulsor
(b) : Turborreactor (Motor a reacción)
Se muestran los componentes principales de la máquina de Brayton, en sus dos alternativas: Turbopropulsor y Turborreactor. Ambos casos son similares hasta el punto 3'. La diferencia estriba en que de allí en adelante, la segunda
turbina es reemplazada por una tobera.
Descripción de los componentes

1-2 El turbocompresor que toma el aire ambiente (a p1 y T1) y lo comprime hasta p2. Este proceso
se puede suponer adiabático. Idealmente es sin roce, pero en general es politrópica con roce.

2-3 Luego el aire comprimido a p2 pasa a la cámara de combustión. Allí se le agrega una cierta cantidad de combustible el que se quema. Al quemarse la mezcla, la temperatura de los gases sube hasta
T3. La combustión es prácticamente isobárica. (o casi isobárica, pues se pierde un poco de presión
por roce). Como a la cámara de combustión entra tanto fluido como el que sale, la presión casi no
varía. La temperatura T3 es una temperatura crítica, pues corresponde a la mayor temperatura en el
ciclo. Además también es la mayor presión. Por lo tanto los elementos sometidos a T3 serán los más
solicitados.

3-4 La expansión de los gases calientes se debe dividir en dos etapas:
 3-3’ Los gases calientes y a alta presión se expanden en la turbina T1. Esta turbina recupera el
trabajo de expansión para accionar el turbocompresor. La expansión en la turbina es hasta las
Ciclos de Turbinas a Gas
Página | 37
Apuntes de Clase
Docente: Emilio Rivera Chávez
condiciones 3'. Idealmente es expansión adiabática sin roce, pero en general es politrópica con
roce.
 En la fase 3´-4 existen dos alternativas:
(a) 3’-4 Los gases de escape se siguen expandiendo a través de una segunda turbina de potencia hasta alcanzar la presión ambiente (p4, evolución 3' - 4). Esta turbina de potencia
entrega trabajo mecánico al exterior. Típicamente el trabajo se usa para accionar un generador o bien otro mecanismo (hélice en el caso de aviones con turbopropulsor o aspas
en un helicóptero). Se trata de un turbopropulsor o lo que comúnmente se llama turbina a gas.
(b) Entre 3' y 4 se sigue con la expansión de los gases en una tobera, el trabajo de expansión se convierte en energía cinética en los gases. Esta energía cinética sirve para impulsar el motor (los gases salen del motor a gran velocidad, produciendo empuje por
efecto del principio de acción y reacción) . Se trata de un turborreactor o lo que comúnmente se llama un motor a reacción.

Finalmente los gases de combustión se evacuan a la atmósfera en 4. La evolución 4-1 es virtual (en
los sistemas de ciclo abierto) y corresponde al enfriamiento de los gases hasta la temperatura ambiente.
SÍNTESIS
El ciclo Brayton es un ciclo de potencia de gas y es la base de las turbinas de gas. Tiene como función
transformar energía química de un combustible en energía mecánica, tiene varias aplicaciones, principalmente en propulsión de aviones, y la generación de energía eléctrica, aunque se ha utilizado también en
otras aplicaciones.
Este puede ser operado de varias maneras, ya sea en ciclo abierto o ciclo cerrado, existen formas de
optimizar su rendimiento, pero hay que tener mucho cuidado en examinar si vale la pena hacer cambios
(desde el punto de vista económico por ejemplo). Una manera de mejorar un ciclo cerrado es la regeneración empleando parte de la energía desechada para calentar los gases que dejan el compresor y, por
ende, reducir la transferencia de calor requerida por el ciclo.
La eficiencia térmica del ciclo Brayton también se incrementa al utilizar compresión de etapas múltiples
con interenfriamiento, y expansión de etapas múltiples con recalentamiento.
Para el mejor estudio de los ciclos de potencia se utiliza una manera idealizada de los mismos en la que
se eliminan ciertos puntos para no complicar su razonamiento, en estas formas de análisis todos los procesos, son reversibles.
Aunque existen formulas para el cálculo de los diferentes parámetros termodinámicos del ciclo, es buena
idea resolver los problemas partiendo de conceptos basados en los principios termodinámicos y las ecuaciones de estado.
Las dos principales áreas de aplicación de las turbinas de gas son la propulsión de aviones y la generación
de energía eléctrica. Cuando se emplea en propulsión de aviones, la turbina de gas produce la potencia
suficiente para accionar tanto el compresor como a un pequeño generador. Los gases de escape de alta
velocidad son los responsables de producir el empuje para impulsar la aeronave.
Biliografía
Ingeniería termodinamica, Francis F. Huang, CECSA, 2003
Termodinamica, Yunus A. Cengel, Michael a. Boles, McGraw-Hill, V edición.
www.braytonenergy.net/about/
Ciclos de Turbinas a Gas
Página | 38
Apuntes de Clase
Docente: Emilio Rivera Chávez
Problemas a resolver
1. A simple Brayton cycle uses helium as the working fluid, has a maximum temperature of 1000 K, and a pressure ratio of 4. At the start of the
compression, the helium pressure and temperature are 50 kPa and 250 K.
Based upon cold-air standard analysis assumptions, the thermal efficiency
of the cycle is:
a) 0.13 b) 0.23 c) 0.33 d) 0.43 e) 0.53
10. Un ciclo ideal de turbina de gas con muchas etapas de de compresión
y expansión, así como con regenerador con 100% de eficacia, tiene una
relación total de presiones de 10. El aire entra en todas las etapas del
compresor a 290K, mientras que a todas las etapas de la turbina lo hace a
1200K. la eficacia térmica de este ciclo de turbina de gas es.
a) 36%
; b) 40%; c) 62%; d) 58%; e) 97%
2. A simple Brayton cycle has a pressure ratio of 5 and a maximum
temperature of 900 K. Air enters the compressor at 100 kPa, 300 K. Based
upon cold-air standard analysis assumptions, the back-work ratio of this
cycle is:
a) 0.11; b) 0.22; c) 0.36; d) 0.42; e) 0.53;
11. Entra aire l compresor de un ciclo regenerativo de turbina de gas, a
300 K y 100 kPa, y se comprime a 800 kPa y 580 K. El regenerador tiene
una efectividad de 72% y el aire entra a la turbina a 1200 K. Para una
eficiencia de la turbina de 86%, determine a) la cantidad de calor que se
transfiere en el regenerador y b) la eficiencia térmica. Suponiendo calores
específicos variables para el aire.
Resp.: a) 152.5 kJ/kg, b) 36.0%
3. A simple Brayton cycle has a pressure ratio of 6, a maximum cycle
temperature of 1100 K, and air enters the compressor at 100 kPa, 300 K.
The isentropic efficiency of the compressor is 0.80 and that of the turbine
is 0.90. Using hot-air standard analysis assumptions, what is the thermal
efficiency of this cycle?
a) 0.27 b) 0.37 c) 0.42 d) 0.55 e) 1
4. A gas turbine power plant operates on a simple Brayton cycle with air as
the working fluid. The air enters the turbine at 1 MPa and 1000 K and
leaves at 125 kPa and 610 K. Heat is rejected to the surroundings at a rate
of 8000 kW and the air flow rate is 25 kg/s. Assuming a compressor
efficiency of 80%, determine the net power output and the thermal efficiency. Assume constant cp.
What-if scenario: How would the answers change if the compressor
efficiency were increased to 90%?
5. Air enters steadily the first compressor of the gas turbine at 100 kPa and
300 K with a mass flow rate of 50 kg/s. The pressure ratio across the twostage compressor and turbine is 15. The intercooler and reheater each
operates at an intermediate pressure given by the square root of the
product of the first compressor and turbine inlet pressures. The inlet
temperature of each turbine is 1500 K and that of the second compressor
is 300 K. The isentropic efficiency of each compressor and turbine is 80%
and the regenerator effectiveness is also 80%. Determine (a) the thermal
efficiency. (b) What-if-Scenario How would the thermal efficiency of the
cycle change if the turbine and compressor efficiency increased to 90%?
Use the ideal gas model for air. What-if scenario: (c) How would the
thermal efficiency of the cycle change if the turbine and compressor
efficiency increased to 90%? Use the ideal gas model for air.
6. Una turbina de gas produce 500 kW de trabajo neto. El aire entra al
compresor a 1 atm y 27 OC e ingresa a la turbina a 7 atm y 927 OC
Usando aire frio estándar responda a la siguiente cuestión a cerca de esta
turbina. ¿Cuál es el flujo másico del aire que pasa a través de la turbina?
¿Cuál es la rata de calor añadido en la cámara de combustión?
Resp.6200 kg/h;
7. Una central eléctrica de turbina de gas opera en un ciclo Brayton simple
con aire como fluido de trabajo y entrega 32 MW de potencia. Las temperaturas mínima y máxima en el ciclo son 310 y 900 K, y la presión de aire
en la salida del compresor es 8 veces el valor a la entrada del compresor.
Suponiendo una eficiencia isentrópica de 80% para el compresor y 86%
para la turbina, determine el flujo másico del aire en el ciclo. Tome en
cuenta la variación de los calores específicos con la temperatura.
8. Al compresor de un motor de turbina de gas regenerativo entra aire a
300 K y 100 kPa, donde se comprime hasta 800 kPa y 580 K. El regenerador tiene un eficacia de 72% y el aire entra a la turbina 1200 K. Para
una eficiencia de la turbina de 86%, determine a) la cantidad de calor
transferido en el regenerador y b) la eficiencia térmica del ciclo. Suponga
calores específicos variables para el aire.
Resp. a) 152.5 kJ/kg; b) 36.0 %
9. En un ciclo Brayton ideal se comprime aire de 100 kPa y 25oC a 1Mpa,
después se calienta a 1200oC antes de que entre a la turbina. Bajo
condiciones de aire frío estándar, la temperatura del aire a la salida de la
turbina en oC es
a) 490;
b) 515
c) 622 d) 763
e) 895
Ciclos de Turbinas a Gas
12. Se desea diseñar una central termoeléctrica de turbina de gas con
recuperación, de acuerdo a las siguientes especificaciones:
Temperatura mínima durante el ciclo
25 0C
Temperatura máxima durante el ciclo
10000C
Eficacia del recuperador
90%
Eficienci
adiabática de laTurbina
90%
Eeg
Eficienci adiabática del compresor
90%
Caída relativa de presión en cada circuito de transferencia de calor 3%
cp = 1.045 kJ//kg-K
K =1.39
Suponiendo que el aire es un gas ideal con calores específicos constantes. Sobre la base de máxima eficiencia térmica del ciclo, determines a) la
eficiencia térmica del ciclo y b) la eficiencia según la segunda ley para la
central, si la fuente es un depósito de calor a 11000C y el sumidero es el
medio ambiente a 298 K.
13. Desarrolle un programa de computadora que permita estudiar el efecto
que tiene la razón de compresión del compresor sobre la eficiencia
térmica en un ciclo cerrado de aire estándar para una central que trabaja
con una turbina de gas.
Correr el programa para una planta con las siguientes características:
Temperatura máxima del ciclo
1200 K
Temperatura mínima del ciclo
300 K
Eficiencia adiabática del compresor
90%
Eficiencia adiabática de la Turbina
90%
Razones de compresión del compresor
4,5,6,7,8,9,10
Grafíquense los resultados y determínense la razón aproximada de
presiones que permita obtener la máxima eficiencia térmica.
14. Desarrolle un programa de computadora que permita estudiar el efecto
que tiene la razón de compresión del compresor sobre la eficiencia
térmica de una planta que opera con una turbina de gas regenerativa.
Correr el programa para una planta con las siguientes características:
Tmax/Tmin
Eficiencia adiabática del compresor
Eficiencia adiabática de la Turbina
Efectividad del regenerador
Eeg
Razones
de compresión del compresor
Razón de clores específicos cp/cv
4.0
90%
90%
90%
2,3,4,5,6,7,8,9,10
1.4
Puede despreciar las caídas de presión. Grafíquense los resultados y
determínense la razón aproximada de presiones que permita obtener la
máxima eficiencia térmica.
15. Considere un ciclo ideal de turbina de gas con dos etapas de compresión y dos etapas de expansión. La relación de presiones a través de cda
etapa del compresor y de la turbina es 3. El aire entra a cada etapa del
compresor a 300 K, y a cada etapa de la turbina a 1200 K. Determine la
relación de retrotrabajo y la eficiencia térmica del ciclo, suponiendo que a)
que no se usa regenerador y b) se usa un regenerador con efectividad del
75%. Use calores específicos variables en ambos casos.
Página | 39
Apuntes de Clase
Docente: Emilio Rivera Chávez
Considere un ciclo Brayton ideal simple que
opera entre los límites de temperatura de 300 K
y 1500 K. Utilizando calores específicos constantes a temperatura ambiente, determine la
relación de presiones para la cual las temperaturas del aire a la salida del compresor y la turbina
son iguales.
Una central eléctrica de turbina de gas opera en un ciclo
Brayton simple con aire como fluido de trabajo y entrega 32
MW de potencia. Las temperaturas mínima y máxima en el
ciclo son 310 y 900 K, y la presión de aire en la salida del
compresor es 8 veces el valor a la entrada del compresor.
Suponiendo una eficiencia isentrópica de 80% para el
compresor y 86% para la turbina, determine el flujo másico
del aire en el ciclo. Tome en cuenta la variación de los
calores específicos con la temperatura.
Un ciclo Brayton con regeneración que emplea aire como
fluido de trabajo tiene una relación de presiones de 7. Las
temperaturas mínima y máxima en el ciclo son 310 y 1150
K. Suponga una eficiencia isentrópica de 75% para el
compresor y 82 % para la turbina, así como una eficacia de
65% para el regenerador, determine a) la temperatura del
aire a la salida de la turbina b) la salida neta de trabajo y c)
la eficiencia térmica del ciclo.
783 K ;180 kJ/kg; 22.5 %
Una central eléctrica de turbina de gas opera en el ciclo
Brayton simple entre los límites de presión de 100 y 1200
kPa. El fluido de trabajo es aire que entra al compresor a
30 C a razón de 150 m3/min y sale de la turbina a 500 C.
Suponga una eficiencia isentrópica del compresor de 82 %,
así como una eficiencia isentrópica de la turbina de 88% y
considere calores específicos variables para el aire para
calcular (a) la salida de potencia neta (b) la relación de
trabajo de retroceso y c) la eficiencia térmica.
659 kW; 0,625; 31.9%
Ciclos de Turbinas a Gas
Página | 40
Apuntes de Clase
Docente: Emilio Rivera Chávez
PROBLEMAS RESUELTOS
Problema 1. Una turbina de gas tiene una eficiencia de 40% en el modo de ciclo simple y produce 159 MW de potencia neta. La
razón de presión es de 14.7 y la temperatura de entrada de la turbina es de 1288 oC. El flujo másico a través de la turbina es de
1536000 kg/h. Tomando las condiciones ambientales como 20 oC y 100kPa, (a) Determine la eficiencia isentrópica de la turbina y
del compresor. (b) también, determine la eficiencia térmica de esta máquina si se añade un regenerador cono una efectividad de
80%
RESOLUCION
Diagrama T -s del ciclo Bryton
Resumen de datos
rp  14.7
  40%
T  293K
;
1
T  1561 K
p  100000Pa

1
kg
hr
J
kg K
cp  1006.2
k  1.4
 159000kW

neto
m  1536000
3
R  287
W
J
kg K
(a) La eficienci a térmica del ciclo Brayton, calculada a partir de la definición, biene dada por::
 
Wneto
Qa
Entonces el Qa se puede calcular a partir de esta ecuación; asi:
W
neto
Qa 
6

Qa  397.5 10 W
A partir del Qa, se puede calcular la temperatura adiabática T2r:

Qa = m cp  T  T
T
2r
3
2r

Qa
 T 
m cp
3
T
2r
 635.1K
La temperatura isentropica T 2, puede ser calculada a partir de:
k 1
T  T  rp
2
k
T  631.52K
1
2
Entonces el ren dimineto isentropico del com presor estará dado por (para calores especificos constantes):
T T
2
1
c 
T T
2r
1
c  0.99
El trabajo de l a turbina se puede calcular a pratir del trabajo neto del sist ema y del trabajo de compresor compresor:
Wneto  WT  WC
El trabajo del compresor:

Wc  m cp  T
Ciclos de Turbinas a Gas
2r
T

1
6
Wc  146.87 10 W
Página | 40
Apuntes de Clase
6
Emilio Rivera Chávez
Wc  146.87 10Docente:
W
Entonces el tra bajo de la turbina será:
Wt  W
neto
 Wc
6
Wt  305.868 10 W
La temperatura adiabatica T4r, será igual a:
T
4r
 T 
3
Wt
y la temperatura isentropica, esta dada por:
0
4r
 848.54 10 K
1 k
k
T  T  ( rp )
4
T
m cp
0
T  724.242 10 K
3
4
Finalmente el rendimiento isentropico de la turbina se puede calcular a p artir la primera ley de la term odinámica,
considerando calores especificos constantes.
T T
3
4r
t 
t  0.851
T T
3
4
b) La adición de un regenerador, sólo afecta a la tempertura de entrade d el aire al quemador, en consecuencia se usa menor
menor cantidad de combustible, en termininos del ciclo termodinámico esto afecta al Qa. (que en tdod caso será menor, por
lo que la eficiencia del sistema aumentará).
T T
 rec 
7
T
4r
2r
T
T
2r
rec  80%
T
T  T
7

Qa  m cp  T  T
W
 
3
neto
Qa
Ciclos de Turbinas a Gas

7
2r

 rec T
4r
T
2r

4r
2r
 848.54K
 635.1K
T  805.852K
7
6
Qa  324.194 10 W
  0.49
Página | 41
Apuntes de Clase
Docente: Emilio Rivera Chávez
Problema 2. Un ciclo Brayton con regeneración que emplea aire como fluido de trabajo tiene una relación de presiones de 7 y
opera entre las temperaturas de 37 oC y 877 oC. Suponga una eficiencia isentrópica de 82% para la turbina y 75% para el
compresor y una eficiencia de 65% para el regenerador. La pérdida de presión en la cámara de combustión es de 2%.
Determine a) la temperatura del aire a la salida de la turbina, b) la salida neta de trabajo y c) la eficiencia térmica.
RESOLUCION
Resumen de Datos
rp  7
T1  ( 37  273)  K;
T3  ( 877  273)  K
t  82%
;  73  98%
r  65%
;
R  287
c  75%
J
; k  1.4
kg K
cp  1006.2
J
kg K
(a) La temperatura T 4, isentropica se cálcula a partir de la temperatura máxima del ciclo:
p 
  3 
T4  p 4 
T3
( k 1) / k
 p
  73 2
 p1



1 k
( k 1) / k

 ( 73rp )(k 1)/ k
T4  T3  73 rp

k
T4  663.358K
La temperatura real a la salida de la turbina se calcula a pa rtir del rendimiento de la turbina:
T 
T3  T4r
T3  T4
 T4 r  T3   T (T3  T4 )
T4r  T3  t ( T3  T4)
T4r  750.954K
(b) Calculamos la te mperatura T2, isentropica:
k 1
T2  T1 rp
k
T2  540.5K
Calculamos ahora la temperatura T2 real a partir del rendimiento del compresor;
C 
T2  T1
T2 r  T1
 T2 r  T1 
(T2  T1 )
C
T2r  T1 
( T2  T1)
c
T2r  617.4K
La temperatura a la salida del recuperador se calcula a partir de su eficiencia.
r 
T7  T2
T4  T2
 T7  T2   r (T4  T2 )
Entonces la tempera tura T7, sera: T7  T2r  r ( T4r  T2r)
T7  704.2K
Calculadas todas las temperaturas, podemos calcular el trab ajo neto y el rendimiento:
Wt  m cp  ( T3  T4r)
Qa  m cp  ( T3  T7)
Wt  401520W
Wc  309276W
Qa  448564W
Wneto  Wt  Wc
 
Wc  m cp  ( T2r  T1)
Wneto
Qa
Ciclos de Turbinas a Gas
3
Wneto  92.244 10 W
  0.206
Página | 42
Apuntes de Clase
Docente: Emilio Rivera Chávez
PROBLEMA 1 (examen III-I/2006) Un ciclo de aire estándar de Brayton opera con una razón de presiones de 5.5.
Con temperaturas máxima y minina de 60 F y 1550 F, respectivamente. Las presión a la entrada del compresor es
de 15 psia. Determine: (a) la eficiencia térmica del ciclo y la razón de trabajo del compresor al trabajo de la turbina si
la eficiencia de la turbina es de 80% y la del compresor es 90%. (b) que pasa con la eficiencia térmica del ciclo si el
rendimiento de la turbina sube a 90% y la del compresor baja a 80%? , justifique su respuesta.
RESOLUCION
Resumen de datos
rp  5.5
T  ( 60  460) ;
Diagrama T -s del ciclo Bryton
p  15
1
1
T  1550  460
3
R  53.3 pie
cp  0.240
lbf
lbm
R
Btu
lbm R
k  1.4
La eficiencia térm ica del ciclo Brayton, calculada a partir de la definición, biene dada por::
 
Wneto
QA
donde el trabajo neto del sistema se puede calcular a pratir del trabajo de la turbina y del compresor:
Wneto  WT  WC
el trabajo de la turbina y compreor reales se pued en calcular a partir de las siguientes ecuaciones:

1 
wT  T c pT3 1  (k 1)/ k 
 rp

wC 
c p T1
C
r
( k 1) / k
p

1
y el calor añadid o en las condiciones planteadas se puede calcular, con la siguiente relación:


( k 1) / k


rp
 1  

Q A  c p T3  T1 1 


 
C


Ahora remplazamos valores numericos, para calcular el rendimiento en las dos sit uaciones planteadas:
a) t  80%
; c  90%
Wt  t cp  T   1 
3



1
k 1 
( rp )
k
 k1 
cp  T 

1
k
; Wc 
 ( rp )
 1

Wt  148.802
Ciclos de Turbinas a Gas
c
Wc  87.019
k 1


 
k


( rp )
 1 
; Qa  cp   T  T   1 

3
1
c



Qa  270.581
Página | 43
Apuntes de Clase
Docente: Emilio Rivera Chávez
El trabajo neto, sera entonces:
Wneto  Wt  Wc
finalmente el rendimiento:
 
Wneto  61.783
Wneto
  0.228 ( 22.8%)
Qa
Razón de trabajo del compresor al trabajo de la tu rbina:
Wc
 0.585
Wt
El sistema tine un razonable grado de practicabili dad (el 58.5% del trabajo generado por la turbina es
destinado a impu lsar el compresor, es decir el sistema puede operara en la realidad).
b)
t  90%
; c  80%
Wt  t cp  T   1 
3



k 1 
k 
( rp )

1
cp  T
Wc 
Wt  167.402
c
 k1 

1 
k
 ( rp )
 1
k 1


 
k


( rp )
 1 
Qa  cp   T  T   1 

3
1
c



Wc  97.897
Qa  259.703
El trabajo neto, sera entonces:
Wneto  Wt  Wc
finalmente el rendimiento:
 
Wneto  69.505
Wneto
Qa
  0.268 ( 26.8%)
Razón de trabajo del compresor al trabajo de la tu rbina:
Wc
Wt
 0.585
Esta relación (pra cticabilidad) se mantiene invariable.
Comentarios: La variación de los rendimientos de la turbina y el compresor, favorecen al rendimineto del
sistema, El incremento del rendimiento de la turbina en un 10% es mas determinante que el decremento
del rendimiento del compresor en el mismo porcentaje. El sistema es más sencible al comportamiento de
la turbina.
Ciclos de Turbinas a Gas
Página | 44
Apuntes de Clase
Docente: Emilio Rivera Chávez
PROBLEMA 2 (examen III-I/2006) Un ciclo regenerativo con turbina de gas opera entre las temperaturas de 1000 C
y 20 C La razón de presiones es 6. La eficiencia de la turbina es de 85% y la del compresor 80%. La efectividad del
recuperador se de 80%, La pérdida de presión en la cámara de combustión es de 2%. Suponiendo que la sustancia
de trabajo es el aire determinar el ciclo, estimando los parámetros no conocidos y calcular el rendimiento térmico.
Resumen de datos
Diagrama T -s del ciclo Bryton
rp  6
T1  ( 20  273)  K;
T3  ( 1000  273)  K
t  85% ;  73  98%
c  80%
r  80% ;
R  287
a
J
; k  1.4
kg K
cp  1006.2
J
kg K
Calculamos la temperatu ra T2, isentropica:
T2  T1 rp
k 1
k
T2  488.9K
Calculamos ahora la tem peratura T2 real a partir del rendimiento del compresor;
C 
T2  T1
T2 r  T1
 T2 r  T1 
(T2  T1 )
T2r  T1 
C
( T2  T1)
c
La temperatura a la salid a del recuperador se calcula a partir de su eficiencia.
r 
T7  T2
T4  T2
T2r  537.842K
 T7  T2   r (T4  T2 )
La temperatura T4, isentropica se cálcula a partir de la temperatura máxima del ciclo:
p 
  3 
T4  p 4 
T3
( k 1) / k
 p
  73 2
 p1



1 k
( k 1) / k
 ( 27 rp )(k 1)/ k

T4  T3  73 rp

k
T4  767.373K
La temperatura real a la salida de la turbina se calcula a partir del rendimie nto de la turbina:
T 
T3  T4r
T3  T4
 T4 r  T3   T (T3  T4 )
T4r  T3  t  ( T3  T4)
Entonces la temperatura T7, sera: T7  T2r  r ( T4r  T2r)
T4r  843.217K
T7  782.1K
m  1
Calculadas todas las temperaturas, podemos calcular el rendimiento:
Wt  m cp  ( T3  T4r)
Qa  m cp  ( T3  T7)
Wt  432448W
Qa  493902W
Ciclos de Turbinas a Gas
Wc  m cp  ( T2r  T1)
 
Wt  Wc
Qa
Wc  246360W
  0.377 ( 37.7%)
Página | 45
kg
s
Apuntes de Clase
Docente: Emilio Rivera Chávez
PROBLEMA 3 (examen III-I/2006) Se desea diseñar una central termoeléctrica que trabaje con una turbina de gas en un ciclo
cerrado
y que utilice
como
sustancia
de trabajo,
de acuerdoque
contrabaje
las siguientes
PROBLEMA
3 Se aire
desea
diseñar
una central
termoeléctrica
con unaespecificaciones:
turbina de gas en un ciclo cerrado y que utilice aire como
Temperatura
el ciclo
C ; Eficiencia
adiabática de la turbina 88 %
sustancia demáxima
trabajo,durante
de acuerdo
con850
lasOsiguientes
especificaciones:
OC ;
Temperatura
durante
el el
ciclo
compresor
%
Temperaturamínima
máxima
durante
ciclo30
850
OC Eficiencia adiabática
Eficienciadel
adiabática
de 85
la turbina
88 %
Suponiendo
quemínima
el aire durante
es un gas
ideal con
calores específicos
constantes
cp= 1.045
y k = 1.39
Temperatura
el ciclo
30 OC
Eficiencia
adiabática
delkJ/kg
compresor
85 %y despreciando las caídas
deSuponiendo
presión: Determínese:
(a)un
la potencia
máxima
del ciclo;
(b) el gasto
de airekJ/kg
por cada
neta desarroque el aire es
gas idealespecífica
con calores
específicos
constantes
cp= 1.045
y k =kW
1.39dey potencia
despreciando
las caídas de presión:
llada;
(c) ¿puede(a)serlaregenerativo
el ciclo?,máxima
¿Por qué?
Determínese:
potencia específica
del ciclo; (b) el gasto de aire por cada kW de potencia neta desarrollada; (c) ¿puede ser
regenerativo el ciclo?, ¿Por qué?
T1  ( 30  273)  K
k  1.39
T3  ( 850  273)  K
t  88%
cp  1045
r  85%
J
kg K
k
T

rpo p t   3 T C 
 T1

k / 2( k 1)
rp   t c

c p T1
C
wneto 
r
( k 1) / k
p
2 ( k 1)

T1 
rp  5.524
1 k 


k 
wt  t cp  T3  1  rp


1 
wT  T c pT3 1  (k 1)/ k 
 rp

wC 
T3 
5
wt  3.934 10 Sv
 k 1 

cp  T1 
k
wc 
  rp
 1

1
5
wc  2.435 10 Sv
c
( wt  wc)
kW s
wneto  149.848Sv
1000
m 
kg
1
m  0.007
wneto
s
2
2
m
Calculamos la temperatura T 2, isentropica:
 Kg 
 s 


 kW 
k 1
T2  T1 rp
k
T2  489.4K
Calculamos ahora la temperatura T 2 real a partir del rendimiento del compresor;
C 
T2  T1
T2 r  T1
 T2 r  T1 
(T2  T1 )
T2r  T1 
C
( T2  T1)
c
T2r  536.047K
La temperatura T4, isentropica se cálcula a partir de la temperatura máxima del ciclo:
T3
(k 1)/ k
 rp 
T4
1 k
T4  T3 ( rp )
k
T4  695.224K
La temperatura real a la salida de la turbina se ca lcula a partir del rendimiento de la turbina:
T 
T3  T4r
T3  T4
 T4 r  T3   T (T3  T4 )
T4r  T3  t  ( T3  T4)
T4r  746.557K
El gas sale con una temperatura mayor a la temperatura de salida del compresor, por lo que puede
aprovecharse, esta energía termica, para sobrecalentar el aire comprimido.
Problema 1. (examen III-II/2006) Una turbina de gas tiene una eficiencia de 40% en el modo de ciclo simple y produce 159
MW de potencia neta. La razón de presión es de 14.7 y la temperatura de entrada de la turbina es de 1288 oC. El flujo másico a
través de la turbina es de 1536000 kg/h. Tomando las condiciones ambientales como 20 oC y 100kPa, (a) Determine la eficien-
Ciclos de Turbinas a Gas
Página | 46
Apuntes de Clase
Problema 1. Una turbina de gas tiene una eficiencia de 40% en el modo de ciclo simple y produce 159 MWDocente:
de potencia
neta. La
razón de
presión
Emilio
Rivera
Chávez
es de 14.7 y la temperatura de entrada de la turbina es de 1288 oC. El flujo másico a través de la turbina es de 1536000 kg/h. Tomando las
cia isentrópica
de la turbina
también,la determine
la eficiencia
térmica
estacompresor.
máquina (b)
si setambién,
añade determine
un rege- la
oC compresor.
condiciones
ambientales
como y20del
y 100kPa, (a)(b)Determine
eficiencia isentrópica
de la
turbinade
y del
neradortérmica
cono una
efectividad
80%
eficiencia
de esta
máquinade
si se
añade un regenerador cono una efectividad de 80%
RESOLUCION
Diagrama T -s del ciclo Bryton
Resumen de datos
rp  14.7
  40%
T  293K
;
1
T  1561 K
p  100000Pa

1
kg
hr
J
kg K
cp  1006.2
k  1.4
 159000kW

neto
m  1536000
3
R  287
W
J
kg K
(a) La eficienci a térmica del ciclo Brayton, calculada a partir de la definición, biene dada por::
 
Wneto
Qa
Entonces el Qa se puede calcular a partir de esta ecuación; asi:
W
neto
Qa 
6

Qa  397.5 10 W
A partir del Qa, se puede calcular la temperatura adiabática T2r:

Qa = m cp  T  T
3
Qa
T  T 
2r

2r
T
m cp
3
La temperatura isentropica T 2, puede ser calculada a partir de:
T  T  rp
2
1
2r
 635.1K
k 1
k
T  631.52K
2
Entonces el ren dimineto isentropico del com presor estará dado por (para calores especificos constantes):
T T
2
1
c 
T T
2r
1
c  0.99
El trabajo de l a turbina se puede calcular a pratir del trabajo neto del sist ema y del trabajo de compresor compresor:
W neto  WT  WC
El trabajo del compresor:

Wc  m cp  T
2r
T

1
6
Wc  146.87 10 W
Entonces el tra bajo de la turbina será:
Wt  W
Ciclos de Turbinas a Gas
neto
 Wc
6
Wt  305.868 10 W
Página | 47
Apuntes de Clase
Docente: Emilio Rivera Chávez
La temperatura adiabatica T4r, será igual a:
T  T 
4r
3
Wt
y la temperatura isentropica, esta dada por:
0
T
m cp
4r
 848.54 10 K
1 k
k
T  T  ( rp )
4
0
T  724.242 10 K
3
4
Finalmente el rendimiento isentropico de la turbina se puede calcular a pa rtir la primera ley de la termo dinámica,
considerando calores especificos constantes.
T T
3
4r
t 
t  0.851
T T
3
4
b) La adición de un regenerador, sólo afecta a la tempertura de entrade de l aire al quemador, en consecuencia se usa menor
menor cantidad de combustible, en termininos del ciclo termodinámico esto afecta al Qa. (que en tdod caso será menor, por
lo que la eficiencia del sistema aumentará).
T T
 rec 
7
T
4r
2r
T
T
2r
rec  80%
T
T  T
7

Qa  m cp  T  T
W
 
3
neto
Qa
7

2r

 rec T
4r
T
2r

4r
2r
 848.54K
 635.1K
T  805.852K
7
6
Qa  324.194 10 W
  0.49
Se deja para el estudiante resolver el siguiente problema:
Problema 2. (examen III-II/2006) Una planta de energía de turbina de gas opera en un ciclo regenerativo ideal con aire como
fluido de trabajo. Entra aire al compresor a 95 kPa y 17 oC, y a la turbina a 760 kPa y 827 oC. El calor se añade al aire a una
razón de 90000 kJ/s. Determine la potencia entregada por esta planta y la eficiencia térmica.
Problema 3. (examen III-I/2006) Un ciclo Brayton con regeneración que emplea aire como fluido de trabajo tiene una relación
de presiones de 7 y opera entre las temperaturas de 37 oC y 877 oC. Suponga una eficiencia isentrópica de 82% para la turbina y
Ciclos de Turbinas a Gas
Página | 48
Apuntes de Clase
Docente: Emilio Rivera Chávez
Problema 3. Un ciclo Brayton con regeneración que emplea aire como fluido de trabajo tiene una relación de presiones de 7 y opera entre
75% para el compresor y una eficiencia de 65% para el regenerador. La pérdida de presión en la cámara de combustión es de
las temperaturas de 37 oC y 877 oC. Suponga una eficiencia isentrópica de 82% para la turbina y 75% para el compresor y una eficiencia de
2%. para
Determine
a) la temperatura
aire en
a la
la turbina, es
b) de
la 2%.
salida
neta dea) trabajo
y c) ladel
eficiencia
térmica.
65%
el regenerador.
La pérdida dedel
presión
la salida
cámara de
de combustión
Determine
la temperatura
aire a la salida
de la
turbina, b) la salida neta de trabajo y c) la eficiencia térmica.
rp  7
T1  ( 37  273)  K;
T3  ( 877  273)  K
t  82%
;  73  98%
r  65%
;
R  287
J
; k  1.4
kg K
cp  1006.2
a)
c  75%
J
kg K
La temperatura T4, isentropica se cálcula a partir de la tem peratura máxima del ciclo:
1 k

T4  T3  73 rp

k
T4  663.358K
La temperatura real a la salida de la turbina se calcula a pa rtir del rendimiento de la turbina:
T4r  T3  t ( T3  T4)
T4r  750.954K
b ) Calculamos la temp eratura T2, isentropica:
k 1
T2  T1 rp
k
T2  540.5K
Calculamos ahora la temperatura T2 real a partir del rendimiento del compresor;
T2r  T1 
( T2  T1)
c
T2r  617.4K
La temperatura a la salida del recuperador se calcula a partir de su eficiencia.
r 
T7  T2
T4  T2
 T7  T2   r (T4  T2 )
Entonces la tempera tura T7, sera: T7  T2r  r ( T4r  T2r)
T7  704.2K
Calculadas todas las temperaturas, podemos calcular el trab ajo neto y el rendimiento:
Wt  m cp  ( T3  T4r)
Qa  m cp  ( T3  T7)
Wt  401520W
Wc  309276W
Qa  448564W
Wneto  Wt  Wc
 
Wc  m cp  ( T2r  T1)
Wneto
Qa
Ciclos de Turbinas a Gas
3
Wneto  92.244 10 W
  0.206
Página | 49
Apuntes de Clase
Docente: Emilio Rivera Chávez
Problema 1.-(Examen) Se conocen los siguientes datos de una turbina industrial de 677 HP, de ciclo
o
o
simple: Temperatura y presión de admisión 60 F y 15 psia.; temperatura de entrada a la turbina 1650 F;
relación de presión del compresor 8/1; rendimiento de compresor 85%, rendimiento de la turbina 88%,
perdida de presión en la cámara de combustión 3%, perdida de presión en el escape 2.5% rendimiento
de la cámara de combustión 96%; rendimiento mecánico de la instalación 98%; potencia calorífica inferior
del combustible 1860 Btu/lb; Suponer que el fluido de trabajo es el aire estándar. Calcular (a) La temperatura del aire al salir del compresor y de la turbina; (b) el rendimiento térmico del sistema, (c) el gasto de
aire y el consumo de combustible por cada libra de aire
p1  15
T1  (60  460)
T3  (1650  460)
R
rp  8
R  53.3 pie

  85%

  88%

c
t
cc
ms
 96%
 98%
Psis  677
qi  1860



23
23
41
41
qent
lbm R
k  1.4
R
T
Btu
cp  0.240
psia
3r
qA
lbf
R
lbm
2r
4
2
 1  3%
4r
 0.97
qper
 1  2.5%
1
qR
 0.975
S
(a) La temperatura a la salida del compresor se puede calcular a partir de la temperatura teórica T2 y
del rendimiento térmico del compresor:
k 1
k
T2  T1 ( rp )
T2  942 R
entonces a partir del rendimiento del compresor, calculamos la temperatura real a la salida el compresor:
c 
T2  T1
T2 r  T1
T2  T1
T2r  T1 

T2r  1016
c
R
(b) La temperatura a la salida de la turbina se puede calcular a partir de la temperatura teórica T4 y del
rendimiento térmico de la turbina:
Cálculo de la temperatura teórica a la salida de la turbina:
T4 
T3
k 1
rp e
k
debido a las caídas de presión, la relación de presión en la expansión no es igual a la relación de presión en la compresión, por lo que procedemos a su cálculo:
p3
p1
=7.566
rp 
p4 
 15.385 psia
p3    8p1  116.4 psia
e
23
p4

41
T4 
T3
k 1
rp e
Ciclos de Turbinas a Gas
T4  1184 R
k
Página | 50
Apuntes de Clase
Docente: Emilio Rivera Chávez
Cálculo de la temperatura real a la salida de la turbina, a partir de la definición de rendimiento:
t 
T3  T4r
T3  T4
T4r  1295 R
T4r  T3    ( T3  T4)
t
(b) El rendimiento termico se puede calcular a partir del calor añadido y el trabajo neto entregado por el
sistema.
 sist 
wc  cp (T2r  T1)
wt  cp  (T3  T4r)
wc  119.14
wt  195.671
Btu/lbm
wturb  wcomp
qA
qent  cp  (T3  T2r)
qent  262.46
Btu/lbm
Btu/lbm
El rendimiento térmico del sistema está dado por:
sist  
wt  wc 
 100
 qent 
El rendimiento total

total
 sist  
sist  29.2 %

ms
total
 28.576%
La masa de aire se puede calcular a partir de la potencia generada, el trabajo neto y el rendimiento
mecánico:
( wt  wc)
Psis    maire
ms
42.41
Psis 42.41
maire 

ms
 ( wt  wc)
maire  1 lbm/min
El consumo de combustible por libra de aire, dosificado o relación combustible aire, se calcula a partir
de un balance de calor:
qent (ma  mc )  qi  mc cc
qent (1 
rc / a 
rc/a =
Ciclos de Turbinas a Gas

mc
m
)   qi  c
ma
m
a


cc


qent
qi  cc  qent
qent
qi 
cc
 qent
 lbm comb
 0.172 
 lbm
aire





Página | 51
Apuntes de Clase
Docente: Emilio Rivera Chávez
PROBLEMA 2.-(Examen) Una Turbina de gas funciona en ciclo abierto regenerativo. Entran 10 kg/seg de
aire en el compresor axial, cuya relación de presiones en la compresión es 8, a la presión de 1 bar y
10ºC; de allí pasa el aire a la cámara de combustión, donde se eleva su temperatura hasta 750ºC,
habiendo atravesado previamente el regenerador, y experimentando desde la salida del compresor a la
entrada en la turbina una pérdida de presión de 0.25 bar. En el flujo de gases de escape de la turbina hay
también una pérdida de presión de 0.1 bar hasta su salida a la atmósfera a través del regenerador.
El rendimiento interno del compresor es 86% y el mecánico 97%. El rendimiento interno de la turbina es
87% y el mecánico 98%. cp = 1,065 kJ/kgºC ; cv = 0,779 kJ/kgºC . La efectividad el regenerador es de
80%. Calcular:
a) El trabajo de compresión y la potencia de accionamiento del mismo
b) La temperatura real del aire a la salida del compresor
c) El trabajo de la turbina y su potencia
d) La eficiencia térmica del sistema.
RESOLUCION
. RESUMEN DE DATOS
T  283K
1
T  1023K
3
rp  8
5
p  10  Pa
m  10
1
p
p
 25 10  Pa
c

  87%
t
4
41
R  287
s
  86%
3
23
kg
 1 10  Pa

re

 80%
mc
mt
cp  1065.2
J
kg K
cv  779
 97%
 98%
k 
cp
cv
J
kg K
J
kg K
k  1.367
(a) Cálculo del trabajo y la potencia del compresor
Clculamos, el trabajo real de compresión, a partir del trabajo isentrópico, y de la eficiencia térmica
WC 
Wisen
 comp

m  (h2  h1 ) cp cte. m  (T2  hT1 )
 
 comp
 comp
donde T2, se calcula a partir de:
( k 1)
k
T  T  ( rp )
2
luego el trabajo de compresión será
1

m cp  T  T
Wc 
Ciclos de Turbinas a Gas
2

 495K

1
6
 2.82  10 W
c
Página | 52
Apuntes de Clase
Docente: Emilio Rivera Chávez
consecuentemente la potencia de accionamiento será
Wc
Pcomp 

6
 2.907 10 W
mc
(b) La temperatura real a la salida del compresor se puede calcular a partir del rendimiento térmico del
compresor
c 
T T
T2  T1
T2 r  T1
T
r
2
 T 

1
2
1
T
r
 548K
2
c
(c) Trabajo y potencia de la turbina
Es necesario calcular previamente la temperatura teórica a la salida de la turbina:
T
3
T 
4
k 1
rp e
k
debido a las caídas de presión, la relación de presión en la expansión no es igual a la relación de
presión en la compresión.
p  p  p
3
2
23
rp 
5
5
y p 4  p 1  p 41  1.1 10 Pa
 7.75 10 Pa
T
T 
4

Wt    m cp  T  T
3
k
  3.87 106 W
4
Pturb  
Luego la turbina entregará un potencia de
 605K
k 1
rp e
t
3
e
 p 3 
rp  7.045
e
 p 4
 
6
mt
 Wt  3.792 10 W
 ciclo 
c ) La eficiencia del sistema (ciclo) se calcula a partir de
Wturb  Wcop
QA
Para calcular el calor agregado es necesario calcular la temperatura real a la salida de la turbinan y la
temperatura del aire a la salida del regenerador, estas temperaturas se pueden obtener a partir de la
eficiencia termica de la turbina y del regenerador respectivamente :
t 
T3  T4 r
T
T3  T4
r
T  T
7
r

2

 T    T  T
3
4
re 4r

T
Entonces el calor agregado será
t
T
r
2

3
3
Ciclos de Turbinas a Gas
r
 660K
4

7
Finalmente la eficiencia térmica del ciclo (sistema)
Wt  Wc 

 
  100
sist 
Q

T
 637K
Q  m cp  T  T
A

4
A


sist
 25.55
Página | 53
Apuntes de Clase
Docente: Emilio Rivera Chávez
PROBLEMA PARA RESOLVER
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
p
T
V
S
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
Ciclos de Turbinas a Gas
Página | 54
Apuntes de Clase
Docente: Emilio Rivera Chávez
PROBLEMA PARA RESOLVER
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
p
T
V
S
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
Ciclos de Turbinas a Gas
Página | 55