Relación Ingresos vs. Costos Totales

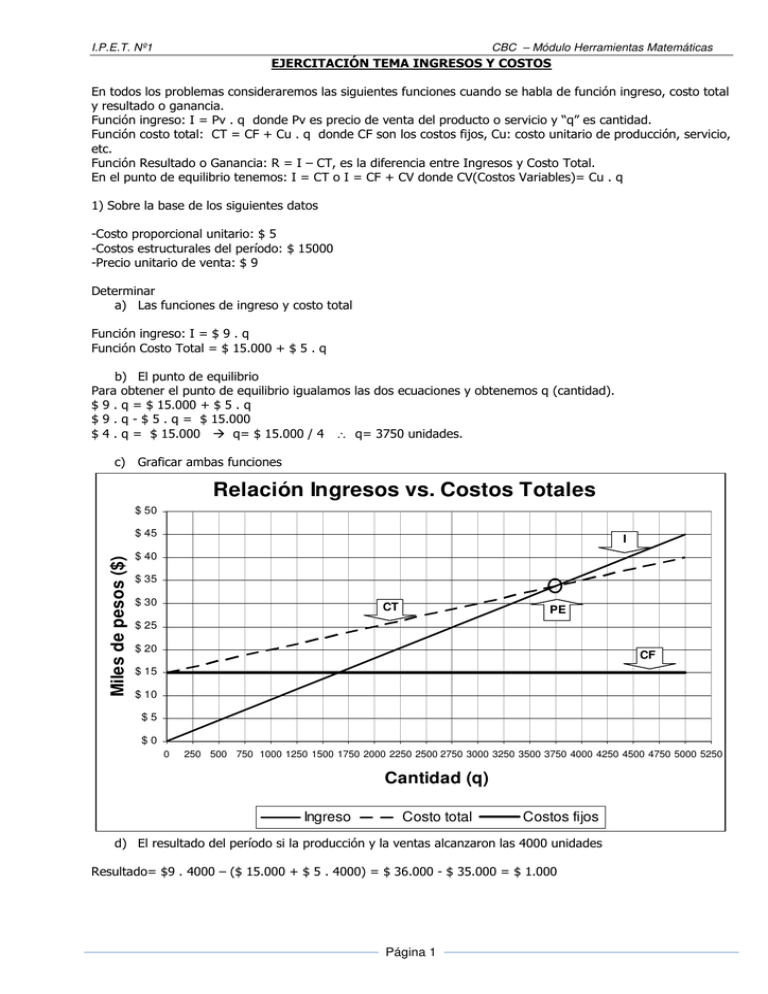
I.P.E.T. Nº1
CBC – Módulo Herramientas Matemáticas
EJERCITACIÓN TEMA INGRESOS Y COSTOS
En todos los problemas consideraremos las siguientes funciones cuando se habla de función ingreso, costo total
y resultado o ganancia.
Función ingreso: I = Pv . q donde Pv es precio de venta del producto o servicio y “q” es cantidad.
Función costo total: CT = CF + Cu . q donde CF son los costos fijos, Cu: costo unitario de producción, servicio,
etc.
Función Resultado o Ganancia: R = I – CT, es la diferencia entre Ingresos y Costo Total.
En el punto de equilibrio tenemos: I = CT o I = CF + CV donde CV(Costos Variables)= Cu . q
1) Sobre la base de los siguientes datos
-Costo proporcional unitario: $ 5
-Costos estructurales del período: $ 15000
-Precio unitario de venta: $ 9
Determinar
a) Las funciones de ingreso y costo total
Función ingreso: I = $ 9 . q
Función Costo Total = $ 15.000 + $ 5 . q
b) El punto de equilibrio
Para obtener el punto de equilibrio igualamos las dos ecuaciones y obtenemos q (cantidad).
$ 9 . q = $ 15.000 + $ 5 . q
$ 9 . q - $ 5 . q = $ 15.000
$ 4 . q = $ 15.000 q= $ 15.000 / 4 ∴ q= 3750 unidades.
c) Graficar ambas funciones
Relación Ingresos vs. Costos Totales
$ 50
Miles de pesos ($)
$ 45
I
$ 40
$ 35
$ 30
CT
PE
$ 25
$ 20
CF
$ 15
$ 10
$5
$0
0
250 500 750 1000 1250 1500 1750 2000 2250 2500 2750 3000 3250 3500 3750 4000 4250 4500 4750 5000 5250
Cantidad (q)
Ingreso
Costo total
Costos fijos
d) El resultado del período si la producción y la ventas alcanzaron las 4000 unidades
Resultado= $9 . 4000 – ($ 15.000 + $ 5 . 4000) = $ 36.000 - $ 35.000 = $ 1.000
Página 1
I.P.E.T. Nº1
CBC – Módulo Herramientas Matemáticas
2) Sobre la base de los siguientes datos
-Costo proporcional unitario de producción: $ 3.20
-Costos estructurales de producción del período: $ 8000.00
-Costos estructurales de administración y comercialización del período: $ 2000.00
Determinar
a) El precio al que deberán comercializarse 5000 unidades para que la empresa se encuentre en equilibrio
En este problema la incógnita es el precio de venta. Planteamos la misma ecuación que el problema anterior.
Los costos fijos es la suma de los dos costos estructurales mencionados.
Función ingreso: I = Pv . 5000
Función Costo Total = $ 10.000 + $ 3,20 . 5000
Igualando y despejando Pv, nos queda:
Pv . 5000 = $ 10.000 + $ 3,20 . 5000
Pv = ($ 10.000 + $ 3,20 . 5000) / 5000 = $ 5,20
El precio a que deberá comercializarse es de $ 5,20. Con ese precio, vendiendo 5000 unidades estaremos en el
punto de equilibrio.
b) Grafique
Relación Ingresos vs. Costos Totales
$ 40
Miles de pesos ($)
$ 35
I
$ 30
$ 25
CT
PE
$ 20
$ 15
CF
$ 10
$5
$0
0
1000
2000
Ingreso
3000
4000
Cantidad (q)
Costo total
5000
6000
Costos fijos
3) Sobre la base de los siguientes datos
-Costo proporcional unitario: $ 14
-Precio de venta: $ 21
-Volumen de ventas previsto: 4000 unidades
Determinar:
a) El monto máximo de cargas estructurales que la empresa puede soportar sin generar quebranto
Es decir cuales son los costos fijos máximos que podemos tener si vendemos/fabricamos 4000 unidades.
I = CT o I = CF + CV entonces CF = I – CV
Reemplazando: CF = $ 21 . 4000 - $ 14 . 4000 = $ 84.000 - $ 56.000 = $ 26.000
Los costos fijos máximos que podemos soportar ascienden a $ 26.000.
Página 2
7000
I.P.E.T. Nº1
CBC – Módulo Herramientas Matemáticas
4) Sobre la base de los siguientes datos
-Costos estructurales: $ 12000
-Costos proporcionales: $ 12
-Precio de venta: $ 18
Determinar
a) El punto de equilibrio
I = CF + CV
Reemplazando: $ 18 . q = $ 12.000 + $ 12 . q
$ 18 . q -$ 12 . q = $ 12.000
$ 6 . q = $ 12.000 -> q = $ 12.000 / $6 = 2000 unidades
b) Cuál es la cantidad de equilibrio si los costos fijos se incrementan en un 20%
CF = $ 12.000 + 20% . $ 12.000 = $ 12.000 + 0,20 . $ 12.000 = $ 12.000 + $ 2.400 = $ 14.400
Con este nuevo valor calculamos el nuevo punto de equilibrio:
$ 18 . q = $ 14.400 + $ 12 . q
$ 18 . q -$ 12 . q = $ 14.400
$ 6 . q = $ 14.400 -> q = $ 14.400 / $6 = 2400 unidades
c) Cuál es la cantidad de equilibrio si los costos proporcionales se incrementan en un 15%
Que los costos proporcionales se incrementen, significa aumentar el costo unitario.
Cu = $ 12 + 15% . $ 12 = $ 12 + 0,15 . $ 12 = $ 12 + $ 1.8 = $ 13.8
Con este nuevo valor calculamos el nuevo punto de equilibrio, manteniendo los valores originales iguales:
$ 18 . q = $ 12.000 + $ 13.8 . q
$ 18 . q -$ 13.8 . q = $ 12.000
$ 4,2 . q = $ 12.000 -> q = $ 12.000 / $ 4,2 = 2857 unidades
d) Cuál es la cantidad de equilibrio si el precio de venta se incrementa en un 10%
Si el precio de venta se incrementen, tendremos:
Pv = $ 18 + 10% . $ 18 = $ 18 + 0,10 . $ 18 = $ 18 + $ 1.8 = $ 19.8
Con este nuevo valor calculamos el nuevo punto de equilibrio, manteniendo los valores originales iguales:
$ 19,8 . q = $ 12.000 + $ 12 . q
$ 19,8 . q -$ 12 . q = $ 12.000
$ 7,8 . q = $ 12.000 -> q = $ 12.000 / $ 7,8 = 1538 unidades
5) Si una empresa tiene $ 9000 de cargas estructurales, un costo proporcional unitario de $ 7.50 y vende sus
productos a $ 10.50, cuál sería la cantidad de productos que debe vender si quiere obtener una ganancia de $
3000.00
R = I – CT = I – (CF + Cu . q)
Reemplazando: $ 3.000 = $ 10,50 . q – ($9.000 + $ 7,50 . q)
Haciendo pasajes de términos y resolviendo:
$ 3.000 = $ 10,50 . q – $9.000 - $ 7,50 . q
$ 3.000 + $9.000 = $ 10,50 . q – $ 7,50 . q
$ 12.000 = $ 3,00 . q q = $ 12.000 / $ 3,00 q = 4000 unidades.
6) Sobre la base de los siguientes datos
-Alquileres: $ 12000
-Costo de adquisición unitario: $ 40
-Teléfono de administración: $ 1600
-Sueldos: $ 3500
-Monotributo : $ 700
-Flete por unidad: $ 5
-Precio de venta: $ 60
a) Clasificar los costos en fijos y variables
Costos Fijos
-Alquileres: $ 12000.00
-Teléfono de administración: $ 1600.00
-Sueldos: $ 3500.00
-Monotributo: $ 700.00
Costos variables
-Costo de adquisición unitario: $ 40
-Flete por unidad: $ 5
Página 3
I.P.E.T. Nº1
Total costos fijos: $ 17.800
CBC – Módulo Herramientas Matemáticas
Total costo unitario: $ 45
b) Hallar la ecuación de la recta de ingresos y costos
Función ingreso: I = $ 60 . q
Función Costo Total = $ 17.800 + $ 45 . q
c) Determinar el punto de equilibrio
Para obtener el punto de equilibrio igualamos las dos ecuaciones y obtenemos q (cantidad).
$ 60 . q = $ 17.800 + $ 45 . q
$ 60 . q - $ 45 . q = $ 17.800
$ 15 . q = $ 17.800 q= $ 17.800 / $ 15 ∴ q= 1187 unidades.
d) Qué cantidad se debe vender para obtener una ganancia de $ 4500
G = I – CT = I – (CF + Cu . q)
Reemplazando: $ 4.500 = $ 60 . q – ($17.800 + $ 45 . q)
Haciendo pasajes de términos y resolviendo:
$ 4.500 = $ 60 . q – $17.800 - $ 45 . q
$ 4.500 + $17.800 = $ 60 . q – $ 45 . q
$ 22.300 = $ 15 . q q = $ 22.300 / $ 15 q = 1487 unidades.
e) Determinar el punto de equilibrio si se otorga una comisión del 10% de cada venta al vendedor.
Al pagarle un 10% al vendedor, debemos asumir esto como un costo unitario más. Por lo tanto tendríamos:
Cu = $ 45 + $ 5 + 10% . $ 60 = $ 45 + $ 5 + 0,10 . $ 60 =$ 45 + $ 5 + $ 6 = $ 51
El costo unitario pasa a ser: $ 51.
$ 60 . q = $ 17.800 + $ 51 . q
$ 60 . q - $ 51 . q = $ 17.800
$ 9 . q = $ 17.800 q= $ 17.800 / $ 9 ∴ q= 1978 unidades.
f) Encontrar la cantidad a vender para obtener una ganancia del 5% de los costos proporcionales.
Podemos considerar el 5% de los costos proporcionales en el punto de equililbrio:
Cantidad de equilibrio: 1187 unidades.
CV = $ 45 . 1187 = $ 53.415
Como deseamos ganar 5% de dichos costos, hacemos: Ganancia = $ 53.415 . 5% = $ 53.415 . 0,5 = $ 2671
Con este dato, realizamos los cálculos:
G = I – CT = I – (CF + Cu . q)
Reemplazando: $ 2.671 = $ 60 . q – ($17.800 + $ 45 . q)
Haciendo pasajes de términos y resolviendo:
$ 2.671 = $ 60 . q – $17.800 - $ 45 . q
$ 2.671 + $17.800 = $ 60 . q – $ 45 . q
$ 20.471 = $ 15 . q q = $ 20.471 / $ 15 q = 1365 unidades.
Página 4