1 VOLUMENES Los cuerpos en el espacio (sólidos) poseen tres

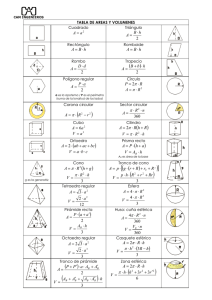
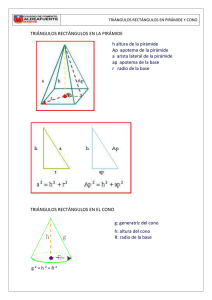
Volúmenes
VOLUMENES
Los cuerpos en el espacio (sólidos) poseen tres dimensiones: largo, ancho y profundidad
POLIEDROS
Un poliedro es un cuerpo limitado por polígonos
Los polígonos que limiten el poliedro, se llaman caras del poliedro.
Los lados de los polígonos se llaman aristas del poliedro
El punto de intersección de dos aristas le llama vértice.
PRISMAS
Un prisma es un poliedro que cumple: Dos de sus caras son polígonos paralelos congruentes
y las otras caras son rectángulos o paralelogramos.
Un prisma es recto cuando las caras laterales son perpendiculares a las bases, o sea que
son rectángulos. En caso contrario el prisma es oblicuo.
1
Volúmenes
Prisma Recto
Prisma oblicuo
PARALELEPIPEDOS
Son prismas cuyas bases son paralelogramos.
ORTOEDROS:
Son prismas en donde todas las caras son rectángulos.
VOLUMEN DE UN PRISMA
El volumen de un prisma es igual al área de la base por la altura
V  Bh
Entonces el área de un ortoedro (una caja) es igual a largo por ancho por altura.
2
Volúmenes
PIRÁMIDES
Son poliedros cuyas caras laterales son triángulos y que tienen una sola base.
Las pirámides tienen distintos nombres, según el número de lados del polígono de la base.
Las pirámides se clasifican en regulares rectas, cuando la base es un polígono regular y la
altura cae en el centro del polígono de la base.
VERTICE O CUSPIDE: Punto donde concurren las aristas laterales.
ARISTA: Segmento de recta común a dos caras
ALTURA: Perpendicular trazada desde la cúspide a la base.
APOTEMA DE LA PIRAMIDE: Es la altura de cualquiera de las caras laterales.
VOLUMEN DE UNA PIRAMIDE:
El volumen de una pirámide es la tercera parte del área de la base por la altura de la
pirámide.
3
Volúmenes
V
Bh
3
SÓLIDOS DE REVOLUCION
EL CILINDRO
Un cilindro circular recto es el cuerpo geométrico resultante
de la rotación de un rectángulo alrededor de uno de sus
lados hasta completar una vuelta.
VOLUMEN DE UN CILINDRO:
El volumen de un cilindro es igual al área de la base por la altura.
V  B  h   r 2h
EL CONO
Si hacemos girar un triangulo rectángulo, una vuelta completa,
alrededor de un de sus catetos, obtenemos un cuerpo geométrico
denominado: cono circular recto o cono de revolución.
VOLUMEN DE UN CONO:
El volumen de un cono es igual a un tercio del área de la base por la altura.
 r 2h
V
3
LA ESFERA:
Si hacemos girar media circunferencia, una vuelta completa, alrededor
del diámetro, obtenemos una superficie esférica
Todos los puntos de la superficie esférica equidistan de un punto fijo
llamado centro y la distancia es el radio.
4
Volúmenes
VOLUMEN DE LA ESFERA:
4
V   r3
3
EJRCICIOS SOBRE VOLUMENES
1. Un recipiente cilíndrico de 30 centímetros de diámetro se llena con agua. A continuación
se sumerge en él una roca, provocando que se derrame algo de agua. Cuando se saca la
roca el nivel de agua en el cilindro descendió 25 cm. ¿Cual es el volumen de la roca?
Respuesta: 17671.459 cm3
2. Una bola metálica hueca y de forma esférica tiene un diámetro interior de 11 cm. y su
espesor es de medio centímetro. Hallar el volumen del metal en la bola. Respuesta:
207.87 cm3
3. Un cilindro recto de 6 m de diámetro y 6 m de altura tiene igual volumen que un cono
recto de 6m. de diámetro. Calcular la altura y la generatriz del cono. Respuesta: 18 m. y
18.25 m respectivamente.
4. Se tiene un prisma regular recto cuyas bases son triángulos. Si el lado de la base es de
20 cm. Calcular el volumen del prisma. La altura del prisma es de 30 cm. Respuesta:
5.160 cm3
5. Calcular el volumen de una pirámide regular triangular, si la apotema de la base mide 5
cm. y la arista de la pirámide mide 12 cm. Respuesta: 287,41 cm3
6. Se tiene un cartón cuya forma es la de un triangulo equilátero de 24 cm. de lado, se
pliega en sus tres ángulos para formar un tetraedro regular. Hallar el volumen del
tetraedro. Respuesta: 144 2 cm3
7. Una esfera está inscrita en un cono circular recto, AB es un diámetro de la base y C es el
vértice del cono. El triangulo ABC es equilátero. Determinar el volumen del cono en
términos de R (el radio de la esfera). Respuesta 3R3
8. ¿Cuantas bolas de cristal de 1.5 cm. de radio caben exactamente en una caja de 162
centímetros cúbicos? Respuesta: 6
9. Se vende café en dos tipos de recipientes cilíndricos. El más alto tiene el doble de altura
que el más bajo, pero su diámetro es la mitad del diámetro del mas bajo. El mas alto
cuesta $ 8000 y el mas bajo $ 12000
¿Cuál es más económico? Explique.
10. Con una cartulina de 12 cm. de ancho por 22 cm. de largo, se pretende hacer una caja sin
tapa. Para ello se recortan cuadrados de 2 cm. de lado en sus cuatro extremos. La caja
así armada que volumen tiene? Respuesta: 288 cm 3
5
Volúmenes
11. Al introducir un trozo de metal en forma de prisma rectangular de 20 cm. de largo por 10
cm. de ancho, en un tanque rectangular en parte lleno de agua, el nivel del agua aumenta
en 2.5 cm ¿Cuál es el volumen y la altura del trozo de metal? Si el largo del tanque es de
80 cm. y el ancho del tanque es de 50 cm. Respuesta 10.000 cm 3 y 50 cm.
12. Un cono de 3 cm. de radio y de 13 cm. de altura, se ha cortado horizontalmente a una
distancia vertical de 4 cm. de la base donde el radio del circulo es 2 cm. ¿Cuál es el
volumen del tronco de cono así formado?
13. ¿Cuál es la longitud máxima que puede tener una barra de acero contenida en una caja
cúbica de 12 cm. de lado? Respuesta: 20.78 cm.
14. Calcular el volumen de un prisma hexagonal regular si la apotema de la base mide 9 cm.
y la altura del prisma mide 48 cm. Respuesta: 13.468,32 cm 3
15. Calcular el volumen de un cubo, si la diagonal de una de sus caras mide 8 cm.
Respuesta: 181,02 cm3
16. La base de una pirámide regular es un cuadrado de lado 6 cm. Calcular su volumen si la
apotema de la pirámide es tres veces el lado de la base. Respuesta: 212,88 cm 3
17. Hallar el volumen de una pirámide regular de base cuadrada, si la apotema de la base
mide 4 cm. y la arista lateral de la pirámide mide 10 cm.
18. Hallar el volumen de una pirámide regular hexagonal, si la apotema de la base mide 10
cm. y la arista lateral de la pirámide mide 20 cm. Respuesta: 1.886,12 cm3
19. Hallar el volumen de una esfera circunscrita a un cilindro circular de 24 cm. de altura y 9
cm. de diámetro de la base. Respuesta: 8.825,77 cm 3
20. Una esfera de 1 cm. de radio está inscrita en un cilindro. ¿Cuál es
volumen del cilindro? Respuesta: 2 cm3
21. Se da un cono circular recto de altura h, de radio de la base R. Se
inscribe en él un cilindro de altura h/3. Demostrar que le volumen del
4
cilindro es
R 2 h .
27
22. Un cono circular recto de altura 8 cm., se puede inscribir en una esfera
256
de 6 cm. de radio. Calcular el volumen del cono. Respuesta:
cm3
3
23. Una esfera de 8 cm. de diámetro se inscribe en cono de 16 cm. de altura. Hallar el
512
 cm3
volumen del cono.
3
6
Volúmenes
24. En un cono circular recto de radio de 6 cm. y altura 12 cm., se inscribe un cilindro de
altura 4 cm. Hallar el volumen del cilindro. Respuesta: 64 cm3
25. Hallar el volumen de un cono circular recto de 4 cm. de radio inscrito en una esfera de
radio
64 2
cm3
3 2 . Respuesta:
3
26. ¿Cuál es la profundidad de una piscina cuyo piso rectangular es de 7 metros de ancho
por 20 metros de largo y cuyo contenido de agua pesa 280 toneladas? (Un volumen de 1
m3 de agua pesa 1 tonelada) Respuesta: 2 m.
27. Un recipiente cilíndrico de 30 cm. de diámetro se llena con agua. A continuación se
sumerge en el cilindro una piedra, provocando que se derrame algo de agua. Cuando se
saca la piedra el nivel del agua en el cilindro descendió 25 cm. ¿Cuál es volumen de la
piedra? Rta: 17.671,46 cm3
28. Que profundidad tiene un corriente de agua si el caudal es de 1.200 litros por segundo, en
un cauce de 1,2 metros de ancho, si la velocidad de la corriente es de 2,2 m/seg.
Respuesta: 0,45 m
29. A un tanque de base rectangular de 180 metros de largo por 80 metros de ancho, llega el
agua por una tubería de 40 cm. de diámetro, con velocidad de 4,50 metros por segundo.
Calcular el tiempo que se necesitara para elevar el nivel del tanque 5 cm. Respuesta:
21,05 minutos.
30.
En esta caja se meten seis latas cilíndricas de jugo. ¿Cuál es la
razón entre el volumen de la caja y los volúmenes de las 6 latas
juntas?
4
Respuesta:

7
Volúmenes
Ejercicios tomados de los siguientes textos:
 Geometría Euclidiana de Hemmerling
 Curso de Geometría. Reunión de profesores
 Geometría de Clemens y otros, de la serie Awli
 Geometría de Edwin E. Moise
Recopilados por: José Manuel Montoya Misas.
8