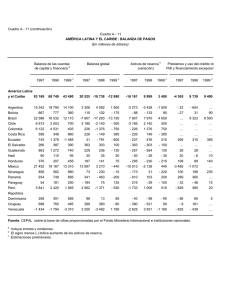
crisis de balanza de pagos y crisis cambiarias

UNIVERSIDAD AUTÓNOMA DE MADRID
FACULTAD DE CIENCIAS ECONÓMICAS Y EMPRESARIALES
DEPARTAMENTO DE ECONOMÍA APLICADA
CRISIS DE BALANZA DE PAGOS Y CRISIS CAMBIARIAS:
“MODELOS DE PRIMERA GENERACIÓN”
APLICACIÓN AL CASO DE EUROPA CENTRAL Y ORIENTAL
Director: D. José Vicéns Otero
Autor: Ainhoa Herrarte Sánchez
Programa de Doctorado en Modelización Económica Aplicada
Instituto Lawrence R. Klein
Octubre 2000
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
INDICE
PRESENTACIÓN
5
CAPITULO I: MODELOS DE CRISIS CAMBIARIAS
10
I.1. MODELOS TEORICOS DE PRIMERA GENERACION: CRISIS DE
BALANZA DE PAGOS_____________________________________________ 12
I.1.1. Modelo de Krugman ................................................................................. 14
I.1.2. Modelo de Flood y Garber......................................................................... 22
I.1.3. Modelo de Connolly y Taylor .................................................................... 29
I.1.4. Modelo de Obstfeld .................................................................................. 36
I.1.5. Esquema típico de un modelo de primera generación................................... 41
I.2. MODELOS EMPIRICOS DE PRIMERA GENERACIÓN _______________ 43
I.2.1. Devaluaciones sucesivas y ataques especulativos sobre el peso mexicano.
Herminio Blanco & Peter M. Garber (1986) ........................................................ 44
I.2.2. Crisis de devaluación y las consecuencias macroeconómicas del proceso de
ajuste posterior sobre los países en desarrollo. Sebastian Edwards y Peter J. Montiel
(1989) ............................................................................................................... 49
I.2.3. Indicadores de alerta de crisis cambiarias. Graciela Kaminsky, Saul Lizondo &
Carmen Reinhart. (1998) .................................................................................... 55
I.3. MODELOS DE SEGUNDA GENERACION: CRISIS CAMBIARIAS
AUTOGENERADAS_______________________________________________ 62
3
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
CAPITULO II: ANÁLISIS DEL RIESGO DE CRISIS CAMBIARIA EN LOS PAÍSES DE
EUROPA CENTRAL Y ORIENTAL
64
II.1. IMPORTANCIA Y CARACTERÍSTICAS DE LA MUESTRA ___________ 65
II.2. DEFINICIÓN DE PERÍODOS DE CRISIS Y PERÍODOS DE CALMA ____ 67
II.3. DEFINICIÓN DE LA VARIABLE ENDÓGENA _____________________ 72
II.4. VARIABLES EXPLICATIVAS___________________________________ 74
II.5. ANÁLISIS INDIVIDUAL DE LAS VARIABLES _____________________ 81
II.6. MODELO PARA LA DETERMINACIÓN DEL RIESGO CAMBIARIO EN
LOS PAÍSES DE EUROPA CENTRAL Y ORIENTAL ___________________ 108
CAPITULO III: CONCLUSIONES
117
BIBLIOGRAFÍA
122
ANEXOS
127
ANEXO I: Matriz de correlaciones .......................................................................... 129
ANEXO II: Salidas EVIEWS. Regresiones logísticas individuales............................. 130
ANEXO III: Salidas EVIEWS: Modelo para la estimación del riesgo cambiario ......... 144
ANEXO IV: Salidas SPSS. Análisis de la Varianza .................................................. 147
ANEXO V: Datos muestrales .................................................................................. 152
4
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
PRESENTACIÓN
Las crisis financieras no son un fenómeno reciente ya que afectan a la economía de los
países desde principios del siglo XVIII1 . A lo largo del siglo XX se han sucedido un buen número
de crisis, - las múltiples crisis del período de entreguerras, la crisis de la libra esterlina y el franco
francés en los años 60, la desintegración del sistema de Bretton Woods a principios de los años 70,
la ruptura del mecanismo de tipos de cambio del Sistema Monetario Europeo, el efecto tequila en
México en 1994-95, etc. En los últimos años se han producido nuevas crisis, - la crisis asiática, la
crisis rusa y su contagio a Latinoamérica -, cuyos efectos sobre la economía mundial siguen
teniendo eco. Por la frecuencia con que se producen y por las importantes consecuencias que
originan en una economía, está fuera de dudas la trascendencia de los estudios e investigaciones en
este ámbito, del que la presente tesina pretende ser una primera y modesta aproximación.
Las crisis financie ras pueden ser de tres tipos: crisis cambiarias, crisis bancarias o crisis de
deuda externa. Una crisis cambiaria es un movimiento especulativo contra una divisa que da lugar
a una devaluación o depreciación de la moneda. Una crisis bancaria es una situación en la que se
producen retiros masivos de depósitos conduciendo a un banco a suspender la convertibilidad de
sus pasivos, o provocando que sea necesaria la intervención de la autoridad monetaria para impedir
tales retiros y evitar de esta forma la quiebra. Por último, las crisis de deuda externa se producen
cuando un país no puede acudir al pago de la deuda contraída con el exterior.
Independientemente del tipo que sean, las crisis financieras reflejan las deficiencias
económicas y financieras de una economía. Además, un tipo de crisis puede venir seguido por
otro. En concreto, existe una fuerte relación entre las crisis cambiarias y las bancarias, ya que éstas
últimas suelen estar precedidas en muchos de los casos por crisis cambiarias, no cumpliéndose la
relación en sentido contrario.
Aunque existen causas comunes que conviven en las crisis financieras acontecidas a lo
largo de la historia, la mayor integración de los mercados financieros y el proceso de globalización
que caracteriza nuestros días, han introducido nuevos rasgos a las crisis de las dos últimas décadas,
haciendo que las crisis de finales del siglo XX difieran en aspectos importantes respecto a las
crisis conocidas hasta el momento. Estas diferencias se basan fundamentalmente en la rapidez de
difusión de los efectos derivados desde unas economías a otras. Entre las causas comunes que
5
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
pueden generar una crisis destaca de manera prioritaria la inestabilidad macroeconómica, en el
sentido de políticas económicas insostenibles entre sí, habiendo sido ésta la causa original de
muchas de las crisis financieras. La debilidad del sistema financiero del país, la inestabilidad
política o la situación financiera mundial, son otras causas comunes que podemos encontrar en la
historia de las crisis.
Por otro lado, las manifestaciones de las crisis cambiarias son comunes en todas las
economías: fuerte depreciación de la moneda, elevación de los tipos de interés internos e
importante disminución de las reservas internacionales del Banco Central. Sin embargo, existen
diferencias fundamentales entre los resultados de las medidas tomadas por las autoridades
monetarias en unos países y en otros. Mientras que en algunos países, tras una devaluación
sustancial de la moneda el tipo de cambio vuelve a estabilizarse, las reservas se recuperan y los
tipos de interés disminuyen, en otros en cambio, tras la devaluación la crisis se agudiza y se hace
más grave cuanto mayor es la depreciación de la moneda, independientemente de los fundamentos
económicos del país.
La gran cantidad de estudios sobre crisis financieras nos ofrecen un conocimiento sobre las
causas que generan una crisis. Sin embargo, las crisis siguen produciéndose y pese a los grandes
esfuerzos de los gobiernos, de los organismos internacionales, y de los académicos por evitarlas,
parece prácticamente imposible poder prevenirlas. De hecho, según Fernández Valbuena 2 , en los
últimos 10 años se ha producido una crisis cambiaria importante cada 19 meses en promedio.
Existen dos corrientes teóricas que pretenden explicar las causas que provocan una crisis
cambiaria, así como proponer mecanismos de alerta que permitan evitarlas. Ambas corrientes no
pretenden excluirse entre sí, sino complementarse. De hecho, los mismos autores cuyas teorías dan
lugar a la primera corriente, completan posteriormente sus trabajos originales añadiendo nuevos
factores explicativos, dando lugar a una segunda corriente de teorías sobre crisis cambiaras. Los
primeros trabajos realizados en esta materia han sido denominados en la literatura económica
como “modelos de primera generación”, mientras que los modelos surgidos posteriormente son
conocidos como “modelos de segunda generación”.
1
En Charles P. Kindleberger “Manías, Pánicos y cracs. Historia de las crisis financieras” puede verse un recorrido
histórico de las crisis financieras desde 1720. Editorial Ariel Sociedad Económica. 1991.
2
Véase Santiago Fernández Valbuena (2000): “Las crisis cambiarias de finales del siglo XX: hechos, teorías y
políticas”. En Lecturas de Economía Aplicada: Referencias a algunas transformaciones derivadas de la Nueva
Economía. Editado por IT&FI (International Technical & Financial Institute).
6
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Los “modelos de primera generación” comienzan con el trabajo original de Paul Krugman
en 1979, en el que explica cómo en una economía que mantiene un sistema de tipos de cambio
fijos, una política fiscal expansiva financiada a través de crédito interno, da lugar a una
disminución gradual de las reservas del Banco Central hasta que éstas se agotan, provocando el
abandono del tipo de cambio fijo y permitiendo la flotación libre de la moneda. El modelo inicial
de Krugman fue completado posteriormente por Flood y Garber (1984), a través de un modelo
lineal con el cual tratan de determinar el momento del tiempo en el que se produce el colapso del
régimen de tipo de cambio, así como el tipo de cambio de la moneda tras el abandono de la
paridad fija. Entre los modelos de primera generación se encuentran también los realizados por
Conolly y Taylor (1984), Maurice Obstfeld (1984), Blanco y Garber (1986), y Edwards y Montiel
(1989) entre otros. Todos estos trabajos encuentran la causa de las crisis cambiarias en la
inconsistencia de las políticas fiscal y monetaria con la política cambiaria.
Los modelos de primera generación sirvieron para explicar las crisis cambiarias de las
décadas de los años 70 y 80. Sin embargo, a partir de principios de los 90, se empiezan a dar
nuevas crisis cuyos rasgos ya no pueden ser explicados totalmente por los modelos originales. Es
en ese momento cuando se inicia una nueva corriente de modelos teóricos, que incluyen como
factor detonante de las crisis cambiarias, no la inconsistencia de las políticas económicas, sino las
expectativas de los agentes. Estos nuevos trabajos, - “modelos de segunda generación” -, se inician
con la aportación realizada por Maurice Obstfeld en 1994, quien explica una situación en la que las
expectativas de los agentes sobre una devaluación de la moneda provocan un incremento de los
salarios con el consiguiente aumento de precios, haciendo que llegue un momento en que al
gobierno le resulte imposible mantener el tipo de cambio y se vea obligado a devaluar la moneda.
Los “modelos de segunda generación” se caracterizan porque definen las crisis como
“crisis autogeneradas”, en el sentido de que son los propios agentes los que provocan un cambio en
la política económica del gobierno a través de sus expectativas. Cuando los agentes prevén que la
moneda va a ser devaluada, se producen determinados efectos sobre la economía (aumento de los
tipos de interés, incremento de los costes salariales, etc.), de tal forma que llega un momento en
que el coste de estos efectos sobre la economía es mayor que el coste que supone para un país
devaluar su moneda, provocando que las expectativas de los agentes condicionen al gobierno y
éste decida devaluar la moneda. Además, si las expectativas de los agentes vienen acompañadas
por unos fundamentos económicos inconsistentes entre sí, la probabilidad de una crisis cambiaria
aumenta. De esta forma, se siguen considerando fundamentales los planteamientos teóricos
iniciales, pero incorporando nuevas variables, y por tanto no se anulan sino que se potencian los
7
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
modelos de primera generación. Entre los modelos de segunda generación se encuentran también
los realizados por Flood y Marion (1997), Bernad Bensaid y Oliver Jeanne (1996), y Obstfeld
(1996) entre otros.
Dado que todo conocimiento de una materia parte del conocimiento de sus fundamentos,
el principal objetivo de este trabajo ha sido el estudio de los primeros modelos o “modelos de
primera generación”, sin olvidar por ello los modelos posteriores. El trabajo que se presenta está
estructurado en tres capítulos. El Capítulo I a su vez está formado por tres apartados: en el primero
de ellos se realiza una revisión de los principales modelos teóricos de primera generación, desde el
modelo inicial de Krugman (1979) hasta los modelos posteriores de Flood y Garber (1984),
Connolly y Taylor (1984) y Obstfeld (1984), para definir a partir de estas teorías el esquema típico
de una crisis de balanza de pagos. El segundo apartado de este primer Capítulo recoge algunas de
las aplicaciones prácticas realizadas de cara a la predicción de una crisis cambiaria a partir de los
fundamentos teóricos definidos por los autores de los modelos de primera generación. Este
apartado incluye tres modelos, de los cuales los dos primeros responden a modelos de primera
generación (Blanco y Garber (1986), Edwards y Montiel (1989)), mientras que el realizado por
Kaminsky, Lizondo y Reinhart (1998) ha sido incluido por ser un estudio tanto de modelos de
primera generación como de segunda, incorporando una aplicación en la que se construye un
sistema de alarma para la previsión de una crisis cambiaria a partir de indicadores de “primera
generación” e indicadores de “segunda generación”. Por último, en el apartado 3 del Capítulo I se
recogen las características de los modelos de segunda generación, así como un breve resumen de
los principios de esta corriente teórica.
En el Capítulo II se ha realizado un modelo econométrico derivado de las teorías de los
modelos de primera generación, cuyo objetivo es predecir el riesgo cambiario en un conjunto de
países de Europa Central y Oriental. La muestra analizada comprende el período desde enero de
1992 hasta junio de 2000. Se trata de un modelo Logit de corte transversal, en el que la variable
endógena es la probabilidad de crisis cambiaria para cada uno de los países, definiendo como crisis
aquellos períodos en los que la variación mensual del tipo de cambio de la moneda de cada uno de
los países respecto al marco alemán haya sido superior al 10%. Dado que el fin último de este
modelo es diseñar una herramienta que permita predecir el riesgo cambiario en el área de Europa
Central y Oriental, las variables explicativas incluidas han sido seleccionadas en función de su
capacidad predictiva. La metodología empleada para la identificación de los mejores indicadores
de cara a la predicción, ha sido la realización de análisis de la varianza (ANOVA) entre cada una
de las variables explicativas y la variable endógena, así como estimaciones logísticas individuales
8
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
de la probabilidad de crisis en función de cada una de las variables exógenas. El modelo final
incluye tres variables, el ratio del crédito interno sobre la oferta monetaria, la variación mensual de
los precios relativos respecto al IPC alemán, y la variación mensual de las reservas del Banco
Central. Los resultados de la aplicación del modelo a período histórico, han sido bastante
favorables, obteniéndose un porcentaje de aciertos sobre el total de la muestra del 88%, y del 80%
durante los períodos de crisis.
Por último, el Capítulo III recoge las conclusiones extraídas a lo largo de todo el trabajo
tanto de los modelos teóricos y empíricos de primera generación, así como las conclusiones
derivadas del modelo realizado para la estimación del riesgo cambiario en los países de Europa
Central y Oriental.
9
CAPITULO I:
MODELOS DE CRISIS CAMBIARIAS
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
I. MODELOS DE CRISIS CAMBIARIAS
Como ya se ha mencionado anteriormente, existen dos planteamientos teóricos para
explicar por qué se produce una crisis de balanza de pagos: “modelos de primera generación” y
“modelos de segunda generación”. Los “modelos de primera generación” defienden que las crisis
cambiarias tienen su origen en políticas macroeconómicas inconsistentes entre sí, y en concreto
una política fiscal expansiva financiada a través de emisión de nueva moneda. Los “modelos de
segunda generación” en cambio, defienden que son las expectativas de los agentes sobre una
próxima devaluación las que provocan que el gobierno se vea obligado a devaluar la moneda
provocando una crisis cambiaria.
El presente capítulo tiene por objetivo describir los fundamentos teóricos de los modelos
de primera generación y una breve descripción de los de segunda, estando estructurado en tres
apartados. En el primero de ellos se hace un análisis individual de los principales modelos teóricos
de primera generación (Krugman (1979), Flood y Garber (1984), Connolly y Taylor (1984), y
Obstfeld (1984)), con el fin de poder extraer las características básicas de las crisis de balanza de
pagos definidas por los modelos de primera generación. El segundo apartado incluye tres
aplicaciones prácticas realizadas en el entorno de los modelos de primera generación. El objetivo
perseguido en cada uno de ellos es distinto, y el grupo de países sobre el que se centran también.
En el primer modelo analizado (Blanco y Garber), se realizan estimaciones de la probabilidad de
devaluación de una moneda bajo un régimen de tipo de cambio fijo y se estiman los distintos tipos
de cambio que prevalecen tras el abandono del sistema de tipos fijos. En el segundo modelo
(Edwards y Montiel), se realiza un análisis del comportamiento de un conjunto de variables
económicas durante los períodos anteriores a una crisis con el fin de caracterizan los períodos precrisis. En este apartado se incluye también el trabajo realizado por Kaminsky, Lizondo y Reinhart,
que aunque no pueda ser catalogado como de primera generación dado que estos autores hacen un
estudio de los modelos de primera y de segunda generación, construyendo además un indicador de
alerta sobre la probabilidad de crisis cambiaria para un amplio conjunto de países. En el tercer
apartado de este capítulo se exponen las características de los modelos de segunda generación así
como un breve resumen de los principales modelos desarrollados en esta línea.
11
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
I.1. MODELOS TEORICOS DE PRIMERA GENERACION: CRISIS DE BALANZA DE
PAGOS
Los mode los sobre crisis de balanza de pagos se fundamentan en que la viabilidad de un
sistema de tipo de cambio fijo se basa en la consistencia entre la política monetaria, fiscal y
cambiaria, en el sentido de que una política fiscal expansiva financiada a través de crédito interno
conduce a una disminución de las reservas del Banco Central que concluye en un abandono de la
paridad fija. Todos los autores defienden que antes de que se produzca el agotamiento total de las
reservas del Banco Central, se produce un ataque especulativo sobre la moneda que acelera el
agotamiento de las reservas, anticipando de esta manera el abandono del tipo de cambio.
Estos modelos parten de una hipotética pequeña economía abierta en la que se cumple el
principio de la paridad del poder adquisitivo, se asume que los precios extranjeros son constantes e
iguales a la unidad, y por tanto el tipo de cambio se iguala al nivel de precios interno, por lo que
las expectativas de inflación se igualan a las expectativas de depreciación. Adicionalmente, estos
modelos parten de la hipótesis de que los agentes poseen expectativas perfectas. La cartera de los
agentes puede estar compuesta por tres tipos de activos: moneda nacional, bonos nacionales y
bonos extranjeros, siendo estos últimos sustitutivos perfectos. Suponiendo un sistema de tipos de
cambio fijos o deslizantes, esta hipotética situación se traduce en que al poseer los agentes
expectativas perfectas, cuando estos prevén que se va a producir un abandono de la paridad fija o
una devaluación de la moneda, deciden cambiar la composición de su cartera, aumentando la
proporción de activos en moneda extranjera y disminuyendo la proporción de activos en moneda
nacional. Para ello acuden al Banco Central, provocando que las reservas comiencen a disminuir,
hasta que llega un momento en que alcanzan su nivel mínimo, de tal forma que el gobierno ya no
puede mantener la paridad generándose una crisis de balanza de pagos. Aunque estos modelos
parten de una economía que mantiene un régimen de tipos de cambio fijos o deslizantes (crawling
peg regime), sus teorías son igualmente aplicables a los sistemas de tipos de cambio flexibles.
El primer trabajo desarrollado sobre crisis de Balanza de Pagos fue el realizado por Paul
Krugman en 1979, demostrando en su modelo cómo bajo un régimen de tipo de cambio fijo, la
financiación del déficit público mediante emisión de nueva moneda, conduce a una disminución
paulatina de las reservas del Banco Central, dando lugar a una pérdida de confianza por parte de
los agentes en el mantenimiento de la paridad de la moneda. Esta pérdida de confianza provoca un
ataque especulativo contra la divisa, que acaba agotando definitivamente las reservas del gobierno,
obligándole a abandonar el tipo de cambio fijo y dejar flotar libremente la moneda.
12
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El modelo planteado por Krugman no consigue llegar a determinar el momento del tiempo
en el que se produce el colapso del régimen, por lo que posteriormente surgen varios trabajos que
intentan ampliar lo inicialmente expuesto por Krugman hasta conseguir determinar cuál es este
momento.
Robert Flood y Peter Garber (1984) plantean un modelo lineal en el que explican que el
colapso de un régimen de tipo de cambio fijo se produce, al igual que decía Krugman, debido a un
exceso de crecimiento de l crédito interno, derivando en una disminución de las reservas del Banco
Central y provocando el colapso del régimen en el momento en que estas se agotan. La aportación
de Flood y Garber respecto al modelo inicial desarrollado por Krugman, es que dichos autores
establecen cómo determinar el momento del tiempo en el cual se produce la caída del régimen, así
como el tipo de cambio de la moneda tras la crisis.
También en 1984, Connolly y Taylor desarrollan un modelo, en este caso partiendo de una
economía bajo un régimen de tipo de cambio deslizante (crawling peg regime), a través del cual
demuestran que cuando el crédito interno crece a un ritmo mayor que la depreciación de la
moneda, se produce un ataque especulativo contra las reservas del Banco Central provocando el
colapso del sistema de tipo de cambio.
Maurice Obstfeld (1984) desarrolla un modelo partiendo del inicialmente planteado por
Flood y Garber, en el que un país que sigue un sistema de tipo de cambio fijo, ante una crisis de su
balanza de pagos, abandona de manera temporal la paridad de la moneda para posteriormente
volver al sistema de tipo de cambio fijo habiendo devaluado previamente la moneda. Su trabajo
estudia cómo las expectativas de los agentes sobre una posible devaluación de la moneda influyen
sobre el momento en que se produce una crisis de balanza de pagos, determinando asimismo este
momento, la magnitud de la devaluación de la moneda y la duración del período temporal de
flotación de la divisa.
A continuación, se analizan de forma individual cuatro de los principales modelos de
primera generación. En cada uno de ellos se ha mantenido la terminología utiliza por los autores
para facilitar el seguimiento de la lectura, en el caso de que se desee acudir a los trabajos
originales.
13
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
I.1.1. Modelo de Krugman (1979)
Paul Krugman, partiendo del modelo original de Salant y Henderson (1978) 3 , estudia el
caso concreto de las crisis de balanza de pagos en una economía bajo régimen de tipo de cambio
fijo, que deriva en el abandono del tipo de cambio. Este trabajo, considerado como fundamental,
ha servido de base para todos los trabajos posteriores de modelización de crisis financieras.
La crisis de balanza de pagos estándar definida por Krugman, se origina por una
disminución progresiva de las reservas de moneda extranjera del Banco Central hasta que éstas se
agotan, haciendo que en ese momento al gobierno le resulte imposible mantener el tipo de cambio.
Antes de que las reservas se agoten totalmente, se produce un ataque especulativo contra la
moneda, adelantando de esta forma el momento en el que éstas se agotan definitivamente. El
ataque especulativo se produce porque los inversores, ante la sospecha de que se va a producir un
abandono del tipo de cambio, deciden cambiar la composición de su cartera, disminuyendo sus
tenencias de moneda interna en favor de moneda extranjera. Este cambio en la composición de las
carteras, se justifica porque cuando el gobierno de un país va a depreciar su moneda, los
especuladores obtienen beneficios derivados de la diferencia entre los tipos de cambio.
El modelo macroeconómico del que parte Krugman posee dos características
fundamentales:
1. La demanda de moneda nacional depende del tipo de cambio
2. El tipo de cambio que equilibra el mercado de moneda interna, varía a lo largo del
tiempo
El planteamiento del modelo arranca de una pequeña economía abierta productora de un
único bien comerciable, cuyo precio es fijado en los mercados internacionales, de tal forma que se
cumple la paridad del poder adquisitivo, es decir, P = sP*, donde “P” es el precio del producto en
el mercado nacional, “s” es el tipo de cambio de la moneda respecto a una divisa extranjera, y
“P*” es el precio del producto en el extranjero. Asumiendo que P* es constante, y transformando
las unidades de tal manera que P*=1, el precio del producto en el territorio nacional queda
igualado al tipo de cambio (P = s).
14
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Se asumen además las hipótesis de precios y salarios flexibles, y nivel de producción de
pleno empleo.
La Balanza Comercial4 (B), que en el modelo planteado por Krugman se corresponde con
la Balanza por Cuenta Corriente, viene definida como la diferencia entre la producción y el gasto:
B = Y - G - C (Y - T, W)
C1 , C2 , > 0
(1)
donde B es la Balanza por Cuenta Corriente, Y el nivel de producción, G el gasto público, C el
consumo privado, T los impuestos y W la riqueza real de los residentes. C1 y C2 son la parte del
consumo que depende de la renta neta y de la riqueza respectivamente.
En el mercado de activos, se parte de que los inversores sólo pueden elegir entre activos
denominados en moneda nacional (M), y activos en moneda extranjera (F), considerando que el
tipo de interés nominal de ambos activos es igual a cero. De esta forma, la riqueza real de los
residentes viene definida por la suma del valor real de las tenencias en moneda nacional (M/P),
más las tenencias de activos en moneda extranjera:
W = M/P + F
(2)
Por último, se asume también que los extranjeros no mantienen moneda nacional en sus
carteras, por lo que M es el stock de moneda interna y en situación de equilibrio los residentes
nacionales deben estar dispuestos a mantener dicho stock.
Partiendo de que las tenencias deseadas de moneda nacional son una proporción de la
riqueza real de los residentes, la condición de equilibrio de la cartera queda determinada por la
siguiente expresión:
M/P = L (π) * W
L<0
3
(3)
Salant y Henderson (1978) plantean un modelo en el que el intento por parte del gobierno de que no se eleve el precio
de un bien no renovable (el oro), obliga a las autoridades a vender oro dando lugar a que las reservas de dicho bien se
agoten.
4
La Balanza Comercial incluye únicamente el comercio de bienes, mientras que la Balanza por Cuenta Corriente incluye
el comercio de bienes y servicios y las transferencias.
15
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Donde π, es la tasa de inflación esperada, que tal y como se ha planteado el modelo (P=s ),
se corresponde con la tasa de depreciación esperada de la moneda.
El estudio desarrollado por Krugman contempla dos regímenes cambiarios distintos:
sistema de tipos de cambio flexibles, en el que el gobierno se abstiene de intervenir el mercado de
divisas para mantener el tipo de cambio, y sistema de tipo de cambio fijo, en el que el Banco
Central se compromete a vender moneda nacional a un tipo de cambio fijo, utilizando para ello sus
reservas de moneda extranjera. Tanto para uno como para otro, realiza un análisis del
comportamiento de la economía en el corto y la rgo plazo.
El análisis del comportamiento de la economía en el corto plazo bajo los dos regímenes
cambiarios se resume a través del siguiente gráfico:
M/P
W
L
A
L’
C
L
B
L’
W
F
La recta LL representa la condición de equilibrio de la cartera de los residentes: en
equilibrio y suponiendo constante la tasa de inflación esperada, un aumento de las tenencias de
moneda extranjera (F) viene acompañado por un aumento de las tenencias reales de moneda
nacional (M/P), ya que si la inflación esperada no varía, no existen motivos para que los residentes
deseen alterar las proporciones de sus tenencias de moneda nacional y moneda extranjera. La recta
WW determina la composición de la riqueza de los residentes: dado un valor fijo de la riqueza,
para aumentar las posesiones de moneda extranjera es necesario disminuir las posesiones reales de
moneda nacional. El punto en el cual se cruzan ambas rectas, es el punto que indica el valor y la
composición de la riqueza de los residentes.
Bajo un régimen de tipo de cambio flexible , el stock de moneda extranjera no puede
variar, ya que el gobierno no se compromete a vender moneda extranjera a cambio de moneda
nacional. En esta situación, si se produjera un incremento de la tasa de inflación esperada, la
moneda nacional sería menos atractiva, desplazando la recta LL hasta L’L’. El nuevo punto de
16
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
corte con la recta WW (punto C) muestra las tenencias de moneda extranjera y nacional deseadas
por los inversores, sin embargo, dado que el stock de moneda extranjera no puede variar, el nuevo
punto de equilibrio no será el punto C, sino el punto B, donde lo único que se ha producido es un
incremento del nivel de precios pero no de la composición de la cartera.
Sin embargo, cuando el tipo de cambio es fijo, el gobierno dispone de unas reservas de
moneda extranjera (R), y está dispuesto a venderlas a cambio de moneda nacional a un precio fijo.
En esta situación, los residentes nacionales sí pueden variar la composición de su riqueza.
Partiendo del gráfico anterior, un incremento de la inflación esperada conduciría a la economía
hasta el punto C, en el que se ha producido un cambio en la composición de la cartera de los
residentes en favor de las tenencias de moneda extranjera. Esta situación provoca un cambio
compensatorio en las reservas del Banco Central que disminuyen exactamente en la misma cuantía
en que aumentan las tenencias de moneda extranjera en manos de los residentes privados:
∆R = - ∆F = ∆ M/P
(4)
Por tanto, bajo un régimen de tipo de cambio flexible, variaciones en las expectativas de
precios se ven reflejadas en el corto plazo en variaciones del tipo de cambio, y bajo un régimen de
tipo de cambio fijo provocan cambios en las reservas del gobierno.
Del mismo modo, Krugman analiza el comportamiento dinámico de la economía bajo
ambos tipos de sistemas:
En el caso de un régimen de tipo de cambio flexible , el tipo de cambio puede variar por
tres motivos:
a) Una variación de la cantidad de dinero en circulación
b) Una variación en las tenencias de moneda extranjera en manos de los residentes
privados
c) Un cambio en las expectativas de inflación
a) Si la creación de dinero depende únicamente de las necesidades de financiación del
gobierno, el crecimiento del stock de dinero vendrá determinado por la diferencia entre los gastos
e ingresos del gobierno:
17
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
M&
= G −T
P
G: Gasto público
(5)
T: Impuestos
Si además se asume que el gobierno ajusta su gasto de tal manera que el déficit público se
mantenga como una constante (g) de la oferta monetaria (M/P=m), entonces se puede expresar que
G - T = gm. Por tanto:
m& = M& / P − (M / P)(P& / P ) = gm − g ( P& / P ) = ( g − P& / P )m
(6)
De esta expresión se deriva que la tasa de variación de los saldos reales depende
únicamente de la tasa de inflación.
b) Tal y como se ha planteado el modelo, la variación de las tenencias de moneda
extranjera bajo un régimen de tipo de cambio flexible, sólo puede venir derivada del intercambio
de bienes, por lo que el crecimiento de las tenencias de moneda extranjera debe ser igual al saldo
de la balanza por cuenta corriente:
F& = B = Y - G - C (Y - T, W)
(7)
c) Por último, para analizar las causas del cambio en las expectativas de inflación, se
asume la hipótesis de “expectativas perfectas”, es decir, que la tasa de inflación esperada coincide
con el crecimiento real de los precios ( π = P& / P ).
Analizando el sistema como un conjunto, se establece una relación entre los saldos reales,
las tenencias de moneda extranjera y la inflación, de tal forma que los residentes sólo estarán
dispuestos a aumentar la proporción de moneda nacional en su cartera si obtienen un mayor
beneficio derivado de una reducción del nivel de precios.
P& / P = π ( m / F )
π<0
(8)
Por tanto, bajo un sistema de tipos de cambio flexible s, la evolución de la oferta monetaria
depende de las expectativas de inflación, y las tenencias de activos extranjeros se igualan a la
balanza por cuenta corriente, lo cual se resume a través de las siguientes expresiones:
18
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
m& = ( g − π ( m / F ))m
(9)
F& = B = Y - G - C (Y - T, W)
(10)
En el caso de un sistema de tipo de cambio fijo, el gobierno posee un stock de reservas de
moneda extranjera (R) que utiliza para mantener el tipo de cambio, lo cual es equivalente a
mantener constante el nivel de precios ( P ).
En primer lugar, Krugman analiza la composición del presupuesto del sector público, así
como del sector privado. El sector privado sólo puede adquirir más activos si disminuye sus
gastos, por lo que el ahorro privado vendrá definido como el exceso de ingresos sobre sus gastos:
S = Y - T - C (Y - T, W)
(11)
Dado que el nivel de precios es constante, el crecimiento de la riqueza de los residentes
equivale al ahorro del sector privado:
W& = M& / P + F& = S
(12)
La distribución del ahorro entre activos denominados en moneda nacional y activos en
moneda extranjera viene determinada por la condición de equilibrio de la cartera (ecuación 3), y
mientras los inversores confíen en que el gobierno va a mantener el nivel de precios, la tasa de
inflación esperada será nula y habrá una relación estable entre la riqueza y las tenencias de dinero.
Por tanto, si se produce un cambio en la riqueza, una proporción L irá destinada a moneda
doméstica, y (1 - L) irá destinado a moneda extranjera, de tal forma que:
W& = M& / P + F& = S
M& / P = LS
(13)
F& = ( 1 − L )S
En el caso del presupuesto público, el gobierno puede financiar su déficit emitiendo más
moneda nacional, o disminuyendo sus reservas de moneda extranjera, por lo que la composición
del presupuesto vendrá expresada del siguiente modo:
M& / P + R& = G − T = g ⋅ ( M / P)
19
(14)
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
De la ecuación (14) se deduce que mientras el gobierno se comprometa a mantener el tipo
de cambio, no posee control sobre cómo se financia su déficit, ya que si el gobierno emite más
cantidad de dinero de lo que los residentes están dispuestos a mantener, los inversores retirarán el
exceso de moneda interna cambiándolo por activos en moneda extranjera al tipo de cambio fijado.
La consecuencia de esto es que la parte del déficit público que queda financiada con reservas
extranjeras, depende de la cantidad de moneda nacional que los residentes estén dispuestos a
mantener:
R& = −( G − T ) + LS
ya que
(15)
M& / P + R& = G − T
La conclusión que extrae Krugman sobre la evolución de la economía bajo un régimen de
tipo de cambio fijo, es que cuando el gobierno incurre en un déficit, sus reservas empiezan a
disminuir aunque el ahorro del sector privado sea igual a cero, y situaciones sucesivas de déficit
hacen que sea imposible fijar el tipo de cambio, independientemente de la cantidad inicial de
reservas que tuviera el gobierno.
Por último, Krugman describe el proceso a través del cual se produce la crisis de balanza
de pagos:
En ausencia de especulación, si una economía está perdiendo gradualmente reservas,
cuando éstas se agotan, se produce un incremento del nivel de precios y por tanto una depreciación
de la moneda, dando lugar a pérdidas de capital para los inversores. Pero dada la asunción de
expectativas perfectas, los inversores ante la disminución de reservas, prevén la depreciación de la
moneda, y deciden cambiar la composición de su cartera vendiendo al Banco Central sus tenencias
de moneda nacional a cambio de moneda extranjera, con el objeto de obtener unos beneficios
derivados de las diferencias en el tipo de cambio, y así evitar pérdidas de capital. Esta situación
provoca que el agotamiento de las reservas del Banco Central se produzca antes de lo que lo
hubieran hecho en una situación sin especulación. Por tanto, si los inversores anticipan
correctamente la depreciación de la moneda, las reservas del gobierno serán eliminadas por un
ataque especulativo.
20
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Las consecuencias del ataque especulativo para el gobierno implican una liquidación de
sus reservas, mientras que para los residentes privados suponen simplemente una alteración de la
composición de su cartera. En concreto, si M y F son las tenencia s de activos de los residentes
justo antes del ataque, y M’ y F’ son sus tenencias después, se deriva que:
M' / P = M / P − R
(16)
F’ = F + R
(17)
Tras el ataque, la economía pasa a un régimen de tipos de cambio flexibles, en el que el
nivel de precios P’ viene determinado por las tenencias de activos:
P’ = M’ G (F’)
(18)
O bien, P' / P = ( M ' / P )G( F' ) = ( M / P − R )G( F + R )
(19)
Dado que no se han producido pérdidas de capital, el ataque especulativo no habrá
provocado variaciones en el nivel de precios, lo que es lo mismo que decir que P' = P o que
P' / P = 1 . Esta condición es la que determina la crisis de balanza de pagos. Bajo un régimen de
tipo de cambio fijo, tanto M / P como F son función de la riqueza W, por tanto la condición
P' / P = 1 , puede ser escrita como función implícita de las reservas y la riqueza:
1 = [L(0)W – R] G [W – L(0)W + R]
La expresión anterior define los límites entre la riqueza y el nivel de reservas.
El siguiente gráfico muestra la evolución de las reservas del Banco Central y la riqueza de
los residentes, desde el momento antes del ataque especulativo hasta después de la crisis:
21
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
m
X
W’
W
A
S
B
S
W’
W
O
F
R
R’
La recta OX representa la situación de la economía bajo un régimen de tipo de cambio fijo
antes del ataque especulativo, y la recta SS representa la situación cuando se ha pasado a un
régimen de tipo de cambio flexible. En el momento del ataque las tenencias privadas de activos
vienen representadas por la intersección entre la recta OX y WW (punto A), mientras que tras el
ataque la situación de la economía pasa a un punto como el B, donde se ha producido un aumento
de las tenencias de moneda extranjera en manos de los residentes así como una disminución de las
tenencias de moneda interna. La diferencia entre las tenencias iniciales de moneda extranjera y las
mismas tras el ataque especulativo, son la pérdida de reservas por parte del Banco Central. En el
caso de que en el momento del ataque la riqueza de los residentes hubiera sido mayor (recta
W’W’), la cantidad de reservas que los residentes tendrían que haber adquirido para que éstas se
agotaran hubiera sido mayor (R’).
I.1.2. Modelo de Robert Flood y Peter Garber (1984)
A partir del trabajo de Krugman, Flood y Garber desarrollan un modelo lineal cuyo
objetivo es determinar el momento del tiempo en el cual se produce el colapso de un régimen de
tipo de cambio fijo. El modelo parte de la hipótesis de expectativas perfectas, y aunque mantiene
los elementos esenciales del trabajo realizado por Krugman, incorpora un nuevo concepto: el “tipo
de cambio sombra”. Para determinar este momento se basan inicialmente en los fundamentos del
mercado, para posteriormente incluir el comportamiento especulativo de los inversores a través de
una variables aleatoria.
22
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El modelo desarrollado por estos autores parte de una pequeña economía en la que se dan
las siguientes características:
−
Régimen de tipo de cambio fijo
−
Se cumple la condición de la paridad del poder adquisitivo
−
Los agentes económicos actúan bajo el supuesto de expectativas perfectas
−
Los activos a los que tienen acceso los residentes nacionales son moneda nacional y
extranjera, así como bonos nacionales y extranjeros
−
El gobierno posee un stock de moneda extranjera con el objeto de mantener el tipo de
cambio
−
Los residentes privados nacionales no mantienen en su cartera moneda extranjera
−
Los bonos nacionales y extranjeros son sustitutivos perfectos
Las ecuaciones de partida del modelo son las siguientes:
Mt
= a 0 − a1i t
Pt
a1 > 0
M t = Rt + Dt
(1)
(2)
D& t = µ
µ>0
(3)
Pt = Pt* S t
(4)
 S& 
*
it = it +  t 
 St 
(5)
Donde M es la oferta monetaria, P es el nivel de precios, i es el tipo de interés, R son las
reservas de moneda extranjera que posee el Banco Central, D es el crédito interno y S es el tipo de
cambio de la moneda interna respecto a la moneda extranjera. P* e i* representan el nivel de
precios y el tipo de interés extranjero. Por último, S& representa la variación temporal del tipo de
cambio. Como se puede observar, la primera diferencia respecto al modelo inicialmente planteado
por Krugman es la incorporación del tipo de interés como variable fundamental en la construcción
del modelo.
La ecuación (1) refleja la condición de equilibrio del mercado de dinero, siendo la parte
derecha de la ecuación la demanda de saldos reales. La ecuación (2) representa la composición de
23
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
la oferta monetaria: reservas de moneda extranjera del Banco Central más el crédito interno. La
ecuación (3) establece la hipótesis de que el crédito interno crece cada período un valor constante
y positivo µ. Por último, las ecuaciones (4) y (5) representan las condiciones necesarias para que
se cumpla la paridad del poder adquisitivo.
Sustituyendo las ecuaciones (4) y (5) en la ecuación (1) se llega a las siguientes
expresiones:

 * S&
*
M t = Pt S t  a0 − a1  it + t
St





 
M t = Pt* S t a0 − Pt* St a1i * − Pt* a1S& t
Igualando a 0 P* − a1 P* i * = β y a1 P* = α se obtiene que:
M t = β S t − α S& t
(6)
Se asume que el nivel de precios extranjero, así como los tipos de interés extranjeros
permanecen constantes, por lo que los coeficientes β y α permanecerán también constantes.
Dado que el modelo parte de un país bajo un régimen de tipo de cambio fijo, el valor de S&
es nulo, por lo que M t = βSt . Sustituyendo esta expresión en la ecuación (2) se obtiene la
ecuación que determina el nivel de reservas extranjeras del Banco Central:
R t = βS t − Dt
(7)
De la ecuación (7) se deduce que cuando el tipo de cambio es fijo, el nivel de reservas se
ajustará en función de las variaciones del crédito interno (D) para mantener el equilibrio del
mercado de dinero (M = R + D). Por tanto, a medida que el crédito interno aumenta, el stock de
reservas irá disminuyendo, y dado que una de las hipótesis del modelo es que el crédito interno
crece una cantidad constante y positiva µ, las reservas irán disminuyendo esa misma cuantía de
manera progresiva hasta que se agoten.
24
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El Banco Central del país mantendrá el tipo de cambio mientras las reservas netas sean
positivas, y en el momento en que éstas se agoten se produc irá el colapso del régimen del tipo de
cambio. A partir de ese momento, el tipo de cambio flotará libremente.
Flood y Garber tratan de determinar el momento en que se produce el colapso del régimen,
así como el tipo de cambio posterior al colapso. La estrategia que siguen es determinar primero el
tipo de cambio inmediatamente posterior al colapso del régimen, suponiendo que dicho colapso se
produce en un momento cualquiera z. A este tipo de cambio flotante lo denominan “tipo de cambio
sombra”.
Si el régimen de tipo de cambio fijo deja de ser viable en el momento z, significa que en
ese momento el stock de reservas del Banco Central se ha agotado. Sin embargo, generalmente el
agotamiento de las reservas se produce antes de ese momento debido a que los agentes, ante la
sospecha de que el tipo de cambio va a ser abandonado, provocan un ataque especulativo contra la
moneda.
Tras el colapso del régimen, el equilibrio del mercado de dinero vendrá determinado por la
ecuación (9), donde z+ indica el momento posterior al ataque especulativo:
M
z+
= β S z + − α S& z +
(9)
Además, dado que el stock de reservas se ha agotado, la oferta monetaria será igual al
crédito interno ( M z + = Dz + ), y por tanto a partir de ahora el stock de dinero crecerá al mismo
ritmo que el crédito interno (µ).
Para calcular el tipo de cambio sombra, Flood y Garber proponen la siguiente expresión:
[
]
S( t ) = αµ / β 2 + M ( t ) / β ,
t≥ z
(10)
Una vez calculado el tipo de cambio sombra, para determinar el momento z en que se
produce el colapso del régimen, parten de que en el momento inmediatamente posterior al colapso
(z+), el tipo de cambio es igual al tipo de cambio fijo ( S z + = S ). Esto es así, porque si el tipo de
cambio Sz+ fuera mayor que el tipo fijo, los agentes al ver que podrían obtener beneficios
potenciales derivados de la diferencia entre los tipos de cambio, adelantarían el colapso del
25
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
régimen antes del momento z. Por el contrario, si Sz+ fuera menor que el tipo de cambio fijo, al no
poder obtener ningún beneficio, los agentes no tendrían incentivos para comprar moneda
extranjera y por tanto el sistema de tipo de cambio fijo se mantendría. A través de esta condición y
recordando que una vez que las reservas se han alcanzado su nivel mímino se produce la igualdad
Mt = Dt , y sustituyendo el valor del crédito interno en el momento t ( Dt = D0 + µt ) en la
ecuación (10), se obtiene el momento del colapso del régimen:
 βS − D 0  α R0 α
 − =
z =  t
−
µ
µ β

 β
(11)
Esta ecuación indica que si se produce un aumento de las reservas iniciales (R0 ), el
momento del colapso del régimen se retrasa, mientras que si aumenta el crecimiento del crédito
interno (µ), el momento del colapso se acelera.
Despejando el valor del tipo de cambio en la ecuación (7), se obtiene que el tipo de cambio
en el momento anterior al colapso del régimen es:
S =
R z − + Dz −
β
(12)
Partiendo de la ecuación (11) que define el momento z del colapso y dado que
Dz − = D0 + µz y Rz − = βS − D z − , se obtiene que la cantidad de reservas en el momento
anterior al colapso del régimen es:
RZ − = αµ
(13)
β
En el siguiente gráfico se representa la trayectoria de las reservas del Banco Central, del
crédito interno y de la oferta monetaria en los momentos cercanos al colapso del sistema de tipo de
cambio fijo. Antes del momento z, la oferta monetaria se mantiene constante, sin embargo sus
componentes varían: el crédito interno crece a una tasa µ, y el nivel de las reservas de moneda
extranjera decrecen a la misma tasa. En el momento z, tanto la oferta monetaria como las reservas
caen a una tasa de αµ / β. Desde el momento en que las reservas se agotan, la oferta monetaria
iguala al crédito interno después del momento z. El eje horizontal del gráfico representa el tiempo,
26
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
siendo R0 /µ el momento en el cual las reservas se agotarían en el caso de que no se produjera un
ataque especulativo contra la moneda. La corrección temporal α / β hace que se acelere el
momento del colapso del régimen asegurando que el tipo de cambio no salte.
M
Crédito interno
αµ
β
D0
R0
Reservas
αµ
β
R 0 /µ
z
α β
Tiempo
Estos resultados están basados en la hipótesis de que el valor del tipo de cambio flotante
depende únicamente de los fundamentos del mercado, sin embargo Flood y Garber incorporan el
comportamiento especulativo de los inversores a través de la inclusión de una variable aleatoria
(A). El planteamiento parte de que el tipo de cambio flotante podría seguir la siguiente ley
dinámica:
S t = A exp[(t − z ) β / α ] + αµ β 2 + M t β
(14)
“A”, cuyo valor inicial es cero, es una constante arbitraria determinada en el momento z.
Entonces el tipo de cambio sombra es ahora:
S t = A + αµ / β 2 + Dt / β
(15)
Al igual que anteriormente, para determinar el momento z en que se produce la caída del
régimen del tipo de cambio, es necesario igualar el tipo de cambio sombra al tipo de cambio fijo:
27
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
R
α
β
z =  0 −  − A
β
α
µ
(16)
A partir de las ecuaciones (12) y (16) se puede determinar el nivel de reservas en el
momento del ataque especulativo:
Rz − = βA +
αµ
β
(17)
La ecuación (16) revela que el momento del colapso depende tanto de los fundamentos del
mercado ( R0 / µ − α / β ), como de la constante arbitraria A. La constante A recoge el
comportamiento que podría causar una indeterminación sobre la trayectoria del tipo de cambio
flotante en los momentos posteriores al colapso. Un aumento del valor de A, provocaría un
adelanto del momento del colapso, haciendo que éste se produjera cuando el valor de las reservas
fuera superior a Rz − , haciendo que el ataque especulativo contra la moneda fuera aún mayor.
En el caso de que el crecimiento del crédito interno fuera nulo (µ=0) y no existiera un
comportamiento especulativo arbitrario, el sistema de tipo de cambio fijo jamás se colapsaría. En
este caso, la ecuación (17) daría lugar a que Rz − = βA , y si µ=0 el nivel de reservas se
mantendría constante en su valor inicial (R0 ), por tanto, el colapso del régimen sólo podría ocurrir
si se produjera un comportamiento especulativo de los agentes que hiciera que A ≥ R0 / β .
La posibilidad de que un comportamiento especulativo arbitrario pueda causar el colapso
de un régimen de tipo de cambio fijo tiene que ver con un argumento clásico a favor de los
regímenes de tipo de cambio fijo. El argumento es que desde el momento en que un tipo de cambio
flexible pueda estar sujeto a fluctuaciones especulativas arbitrarias, el tipo de cambio debería ser
fijado con el fin de proteger los sectores de la economía. El análisis realizado por Flood y Garber
indica que un comportamiento especulativo arbitrario idéntico al que se podría manifestar bajo un
régimen de tipo de cambio flexible, se puede producir en un régimen de tipo de cambio fijo
provocando además la indeterminación del momento en el cual se produce el colapso del régimen.
28
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
I.1.3. Modelo de Michael Connolly y Dean Taylor (1984)
El modelo planteado por Connolly y Taylor parte de una economía en la que se sigue un
régimen de tipo de cambio deslizante (crawling peg regime), es decir, la moneda es devaluada a lo
largo del tiempo, pero la tasa de depreciación es anunciada con anterioridad, por lo que los agentes
conocen cuál va a ser el nuevo tipo de cambio.
Connolly y Taylor demuestran cómo cuando el crédito interno crece a un ritmo mayor que
la depreciación de la moneda se produce un colapso del régimen del tipo de cambio, seguido por
un ataque especulativo contra las reservas del Banco Central que provoca que el colapso del
régimen se produzca con anterioridad a una situación en ausencia de especulación.
El modelo que estos autores plantean parte de las siguientes hipótesis básicas:
−
La riqueza monetaria (W) de los agentes está constituida por sus tenencias de moneda
nacional (M) así como por moneda extranjera expresada en moneda nacional (F).
W=M+F
(1)
F = rF*,
(2)
donde F* es el stock de divisas extranjeras y r es el tipo de cambio de la moneda nacional
respecto a la moneda extranjera.
−
Las tenencias de moneda nacional (M) en manos de los residentes son una proporción K de la
riqueza monetaria de los agentes, dependiendo esta proporción del tipo de cambio (r), de tal
forma que cuanto más se deprecie el tipo de cambio, menor será la proporción de tenencias de
moneda interna.
M = KW
(3)
 1  dr 
K = k   
 r  dt 
k<0
29
(4)
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
−
Se asume además que los precios son constantes a nivel internacional, por lo que la riqueza
monetaria en manos de los residentes es constante en términos reales:
W = wr
−
(5)
Los activos de las autoridades monetarias nacionales son iguales a sus pasivos, por lo que:
M=R+C
(6)
siendo R es el stock de reservas del Banco Central y C el crédito interno
−
Durante el régimen de tipo de cambio deslizante, el tipo de cambio se deprecia a la tasa
preanunciada (γ), por tanto r = ~
r e γt , donde ~
r es el tipo de cambio inicial.
−
Del mismo modo, se asume que el crédito interno crece a la tasa γ + ε
El colapso del régimen, seguido de un ataque especulativo contra las reservas del Banco
Central, se produce cuando ε > 0, lo que significa que el crédito interno está creciendo a un ritmo
mayor que lo que se deprecia la moneda nacional, y dado que M = R + C, un crecimiento del
crédito interno (C) implica una disminución de las reservas (R), por tanto a medida que el crédito
interno crece en exceso, el stock de reservas del Banco Central va disminuyendo hasta llegar a la
situación en que se produce el colapso del régimen del tipo de cambio. Mientras la tasa de
depreciación de la moneda sea γ, los agentes mantendrán su equilibrio monetario de acuerdo a la
ecuación M = KW, forzando su ahorro a la adquisición de moneda nacional extra a la tasa γ, pero
no a una tasa mayor ya que incurrirían en un déficit comercial.
Si la política monetaria del gobierno es demasiado expansiva, el régimen del tipo de
cambio deslizante se colapsará y el país pasará a un régimen de tipo de cambio completamente
flexible. En el momento en que se produce el colapso del régimen la tasa esperada de inflación se
sitúa en γ + ε, donde ε es el exceso de crecimiento de crédito interno, y los agentes cambiarán la
composición de su cartera de equilibrio liberándose del exceso de moneda nacional a través de
compras de divisas extranjeras al Banco Central.
30
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Esto significa que durante el régimen de tipo de cambio deslizante, k se mantiene
constante, mientras que después del colapso su valor cae hasta un nuevo punto de equilibrio.
El planteamiento desarrollado por Connolly y Taylor parte también de que los agentes
actúan bajo el supuesto de expectativas perfectas. En su trabajo analizan el proceso de ajuste de un
régimen de tipo de cambio deslizante a uno de tipo de cambio flexible, cuáles son las condiciones
que provocan una crisis de confianza en el régimen de tipo de cambio, prediciendo asimismo el
momento del tiempo en que se pasa de un régimen de tipo de cambio deslizante a un régimen de
tipo de cambio flexible.
Para explicar el proceso del colapso del régimen del tipo de cambio, analizan inicialmente
el comportamiento de las reservas de moneda extranjera a través de su relación con el crédito
interno.
En primer lugar, asumen que en el momento t = 0 el sistema se encuentra en equilibrio,
siendo la tasa de crecimiento del crédito interno y la depreciación de la moneda iguales a γ. Tras
este momento t=0, la tasa de creación de crédito interno se incrementa a γ + ε.
Mientras la tasa de depreciación de la moneda sea constante, los agentes mantienen sus
saldos monetarios en una proporción constante al tipo de cambio. Las tenencias de activos
extranjeros en manos del público se aprecian de forma proporcional al tipo de cambio y por tanto
ni adquirirán ni venderán moneda extranjera, lo que significa que:
dF *
= 0
dt
Un exceso de crédito interno provoca un déficit de la Balanza de Pagos, dando lugar a una
salida de reservas igual a ese déficit en moneda extranjera.
Combinando las ecuaciones (3) y (5), se obtiene que M = k w r, y dado que M = R + C,
entonces:
M=R+C =kwr
(7)
31
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Como el sistema está inicialmente en equilibrio:
~
~
R + C = kw~
r
(8)
~ ~
donde R, C y ~
r representan los valores iniciales de las variables en el momento t = 0.
Si el crédito interno crece a una tasa γ + ε, y el tipo de cambio se deprecia a la tasa γ, la
ecuación anterior puede expresarse como:
~
C = Ce ( γ + ε )t
r = ~
r e γt
~
R = kw~
r e γt − C e (γ + ε ) t
(9)
Por tanto:
~
~
R = Meγ t − Ce (γ + ε )t
(10)
~
~
R = ( M − Ce εt )eγ t
o bien:
(11)
~
donde M es el stock inicial de dinero.
Una vez conocida la relación entre las reservas y el crédito interno, Connolly y Taylor
plantean que se pueden dar tres situaciones alternativas:
1) Que la política crediticia sea consistente con la tasa de depreciación deslizante del tipo de
cambio, es decir, que ε = 0. En este caso las reservas vendrían determinadas por la siguiente
expresión:
~
~
R = ( M − C )e γt
(12)
~
o bien: R = R eγ t
(13)
Esto significa que el valor nominal de las reservas crecerá a la tasa de cambio deslizante
(γ), lo que signigicaría que las reservas de moneda extranjera permanecerán constantes. En
32
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
consecuencia, la preanunciada tasa deslizante implica que si el crédito interno crece a esa misma
tasa se mantendrá el equilibrio.
2) Que la política sobre la evolución del crédito interno sea más expansiva que la tasa de cambio
deslizante, es decir ε > 0. Si el crédito interno crece a una tasa mayor que lo que se deprecia el
tipo de cambio se origina un déficit y las reservas vendrán determinadas por:
~
~
R = Meγ t − Ce (γ + ε )t
(14)
De esta ecuación se deduce que dado que el crédito interno crece más rápido que el stock
de dinero, las reservas comienzan a disminuir.
En términos de reservas en moneda extranjera R* (R = r R*), éstas caen inmediatamente y
esto pesa más que la revaluación de las reservas en moneda nacional. Sin embargo, antes de que
las reservas sean iguales a cero, en el momento t’, el régimen del tipo de cambio se colapsará, ya
que todos los agentes saben que una situación así es insostenible, precipitando por tanto el colapso
del régimen.
Partiendo la ecuación (14), el momento t’ vendrá determinado por la expresión:
[
~
~
~
ln ( R + C ) / C
t' =
ε
]
(15)
3) La ultima alternativa que estos autores plantean es que ε < 0, lo que significaría que las
reservas del Banco Central crecerían de acuerdo a la expresión:
~
~
R = ( M − Ce εt )eγ t
(16)
De esta forma, la tasa de crecimiento de las reservas sería:
 1  dR 
C 
 
 = γ − ε 
 R  t 
R
33
(17)
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
y por tanto la tasa de variación de las reservas en moneda extranjera (R* ) sería:
 1  dR * 
C


= −ε  
*  dt 
R
 R 

(18)
Una vez analizado el comportamiento de las reservas de moneda extranjera pasan a
determinar el momento en que se produce el colapso del régimen. Siempre que la tasa de creación
del crédito interno sea mayor que la tasa de depreciación del tipo de cambio deslizante, la situación
será insostenible haciendo que las reservas tiendan a cero. Sin embargo, antes de que se produzca
el agotamiento completo de las reservas, los individuos bajo el supuesto de expectativas perfectas
anticipan el abandono del régimen de tipo de cambio y su comportamiento especulativo ante esta
situación precipita el colapso monetario.
En ausencia de especulación, antes de que se produzca el colapso del régimen, la cantidad
deseada de moneda nacional en función de los precios (r) viene determinada por la expresión K(γ)
= k(γ)w, siendo γ la tasa esperada y realizada de depreciación del tipo de cambio. Cuando se
agotan las reservas del Banco Central, el tipo de cambio varía y los saldos monetarios vendrán
determinados en función de K (γ + ε) = k (γ + ε)w, donde γ + ε es la nueva tasa de depreciación.
Sin embargo, dado que se ha establecido la hipótesis de expectativas perfectas, los agentes prevén
el colapso del régimen y ante la posibilidad de obtener beneficios, antes de que se deprecie el tipo
de cambio, compran activos en moneda extranjera, haciendo que las reservas del Banco Central se
agoten antes de lo que lo hubieran hecho en ausencia de especulación. Esta situación precipita el
colapso del régimen.
Posteriormente, la economía pasa a un régimen de tipo de cambio flexible en el que los
agentes poseen menos saldos reales debido a la mayor tasa de depreciación de la moneda y con
una tasa de inflación γ + ε.
Connolly y Taylor plantean que el momento en que se produce el colapso del régimen
puede ser calculado. Para ello parten de las ecuaciones que determinan la condición de equilibrio:
~
~
~
~
R + C = M = k (γ )W
~
W = w~
r,
y
~
~
R + C = k (γ ) w~
r
34
(a)
por tanto:
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Inmediatamente después del colapso del régimen, el crédito interno ha crecido a la tasa de
depreciación γ + ε, hasta igualarse a la demanda de dinero. Las reservas extranjeras se ven
reducidas en el momento, y el nuevo punto de equilibrio vendrá determinado por las expresiones:
~
M = C = Ce (γ + ε )t = k (γ + ε )W
W = w~r eγ t
y
Consecuentemente:
~
Ce (γ + ε )t = k (γ + ε ) w~
r eγt
(b)
Dividiendo la ecuación (b) entre la ecuación (a) y multiplicando el resultado por
~
~
~
( R + C ) / C eγt , tomando logaritmos y dividiendo el resultado por ε, se obtiene el momento del
colapso del régimen y el paso a un régimen de tipo de cambio flexible:
~
~ 
  k (γ + ε ) R

+
C
 ln 

~
  k (γ )
C
 
t* =  
ε
(20)
Por lo que el momento del colapso vendrá determinado por la expresión:
[
]
~ ~
t * = −α * + ln( R / C ) + 1) ε
(21)
donde α* indica la sensibilidad de la demanda de dinero respecto a la tasa de depreciación. De esta
expresión se derivan tres conclusiones:
El momento del colapso se produce antes cuanto:
−
Mayor es la sensibilidad de la demanda de dinero respecto a la tasa de inflación.
−
Mayor es la tasa de crecimiento del crédito interno respecto a la tasa de depreciación
deslizante.
−
Menor es el stock de reservas en moneda extranjera respecto al crédito interno.
35
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Conclusiones:
Las principales conclusiones derivadas del trabajo desarrollado por Connolly y Taylor son
las siguientes:
•
Una regla específica sobre la variación del tipo de cambio implica una política monetaria
específica.
•
Si esta política no se sigue, se producirá un colapso del régimen de tipo de cambio deslizante.
•
El colapso del régimen se produce en un momento determinado sujeto a predicción, como
consecuencia de un repentino ataque especulativo sobre las reservas del Banco Central.
•
Tras el colapso, se pasa a un régimen de tipo de cambio flexible.
I.1.4. El modelo de Maurice Obstfeld (1984)
El trabajo desarrollado por Obstfeld parte del modelo lineal inicialmente desarrollado por
Flood y Garber (1984), en el que se establece la hipótesis de una pequeña economía abierta que
sigue una política cambiaria de tipo de cambio fijo, y en la que un déficit continuado de su balanza
de pagos conduce a una crisis de la misma, en la que los especuladores huyendo de la moneda
interna adquieren una gran proporción de las reservas del Banco Central, obligando a la autoridad
monetaria a devaluar la moneda. Sin embargo, a diferencia de Flood y Garber, en el trabajo de
Obstfeld esta devaluación no conlleva un abandono del tipo de cambio fijo, sino que pasando por
un período de transición durante el cual el tipo de cambio fluctúa libremente, de nuevo se vuelve a
un régimen de tipo de cambio fijo aunque con un tipo de cambio devaluado. Una característica
importante de su análisis, es que durante el período de flotación el tipo de cambio sobrepasa el tipo
de cambio tras la devaluación.
Obstfeld trata de determinar el momento del tiempo en el cual se produce la crisis de
balanza de pagos, en función de la cuantía de la devaluación esperada (cuanto mayor es la
devaluación esperada antes se produce la crisis de balanza de pagos), y en función de las
expectativas sobre la duración del período de transición durante el cual el tipo de cambio flota.
36
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Hipótesis del modelo:
−
Pequeña economía abierta en la que los agentes actúan bajo el supuesto de expectativas
perfectas.
−
Existe un bien único de consumo producido tanto por productores nacionales como
extranjeros.
−
Sólo existen dos activos disponibles: activos en moneda nacional (sólo en manos de residentes
internos), y activos extranjeros, cuyo valor en moneda nacional es fijo.
−
El precio del bien de consumo en moneda nacional (P) es igual al tipo de cambio de la
moneda interna respecto a la moneda extranjera (E) por el precio del bien en moneda
extranjera (P*): P = EP*. Se asume que el valor de P* es constante y exógeno, y por
conveniencia se adopta la normalización P* = 1.
−
El tipo de interés de los bonos en moneda extranjera es constante e igual a cero.
−
La demanda de saldos monetarios reales es una función decreciente de la depreciación
esperada del tipo de cambio, donde E& t es la variación del tipo de cambio:
M td / E t = α − β ( E& t / E t )
De estas condiciones de partida se deduce que un crecimiento de la tasa de inflación
interna conduce a que los agentes dediquen una proporción mayor de la composición de su cartera
a activos en moneda extranjera.
−
Por último, la oferta monetaria viene determinada por la siguiente expresión, donde D es el
crédito interno y R son las reservas de moneda extranjera que posee el Banco Central valorada
en moneda nacional al tipo de cambio fijo:
M ts = Dt + Rt
En situación de equilibrio se cumple que
M td = M ts = Dt + Rt .
El Banco Central
&
establece que el crédito interno crece siempre a la tasa constante y positiva µ ( D
t
regla de comportamiento se cumple siempre bajo un régimen de tipo de cambio fijo.
37
= µ ), y esta
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Bajo un régimen de tipo de cambio fijo con movilidad perfecta de capitales, el stock de
reservas extranjeras (R) es una variable endógena que varía de manera discontinua en función de
cómo los residentes cambian la composición de su cartera en respuesta a shocks presentes o
anticipados sobre la evolución del tipo de cambio.
Sin embargo, el crédito interno es una variable predeterminada que debe variar de manera
continua de acuerdo a la tasa µ.
Si el tipo de cambio se fija inicialmente en el valor E , de tal forma que E& / E = 0 , los
saldos monetarios serán constantes de acuerdo a la siguiente expresión:
M = αE
Mientras el tipo de cambio se mantenga fijo, dado que M ts = Dt + Rt , el stock de reservas
disminuye a la tasa µ, por tanto R&t = −µ . La pérdida de reservas se refleja en una continua salida
de capitales del sector privado, y la paridad fija deberá ser abandonada una vez que el stock de
reservas destinado a defender el tipo de cambio se haya agotado. Obstfeld, al igual que Salant y
Henderson (1978) y Krugman (1979), señala que el colapso del régimen de tipo de cambio trae
consigo una crisis de balanza de pagos, en la que los residentes nacionales adquieren rápidamente
la parte de reservas no destinada a la defensa del tipo de cambio.
El momento preciso en que se produce la crisis depende de las expectativas que tengan los
agentes sobre la política que seguirá el Banco Central ante el agotamie nto de las reservas. El
trabajo desarrollado por Krugman se fundamenta en el caso en el que el Banco Central decide
retirarse permanentemente de los mercados de divisas tras el colapso, sin embargo, el modelo
planteado por Obstfeld estudia las diferentes políticas que puede adoptar el Banco Central, y cómo
éstas afectan al momento del ataque especulativo.
Normalmente los bancos centrales no comprometen todo el stock de reservas para
defender un tipo de cambio que ya no es defendible, sino que lo normal es que el Banco Central se
retire del mercado de divisas una vez que se produce una crisis de balanza de pagos que haya
dejado el stock de reservas en un nivel peligrosamente bajo. Tras un período transitorio de
flotación, el tipo de cambio es devaluado formalmente y de nuevo se fija un nuevo tipo de cambio
fijo. El establecimiento de un tipo de cambio realista debería provocar inicialmente una entrada de
38
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
capitales, pero a no ser que la devaluación de la moneda venga acompañada por una política
macroeconómica restrictiva apropiada, se producirán otras crisis de forma inevitable.
Para determinar cuál es el momento en que se produce el ataque especulativo inicial,
Obstfeld parte de una serie de hipótesis adicionales sobre la información de que disponen los
agentes:
−
Los agentes conocen con exactitud cuánto va a durar el período transitorio de flotación
(τ).
−
Los agentes conocen cuál va a ser la cuantía de devaluación del tipo de cambio tras el
período de flotación ( E' > E ).
−
Por último, se asume que los agentes conocen cuál es el nivel de reservas al cual el Banco
Central abandona la paridad fija.
Partiendo del momento t = 0, el momento T en que se produce la crisis se calcula de
manera retrospectiva. La solución está en que bajo la hipótesis de expectativas perfectas , los
agentes nunca podrían prever una variación del tipo de cambio, ya que un cambio del tipo de
cambio, si es anticipado, proporcionaría a los agentes una oportunidad de obtener beneficios
inconsistente con la hipótesis de equilibrio. Este principio implica dos restricciones sobre la
trayectoria de la economía. En el momento T, cuando el Banco Central permite que el tipo de
cambio fluctúe, el tipo de cambio E debe ser ET para equilibrar el mercado de activos.
Adicionalmente, a medida que t se aproxima a T + τ (momento en el cual el Banco Central entra
de nuevo en el mercado de divisas), el tipo de cambio flexible de equilibrio Et debe tender al
nuevo valor E' . Solamente la tasa de depreciación ( E& / E ) puede variar.
Para calcular el momento T en que se produce la crisis de balanza de pagos, primeramente
analiza el comportamiento del tipo de cambio durante el período de transición, aplicando
ecuaciones diferenciales a la ecuación M td / Et = α − β ( E& t / E t ) . Finalmente, el momento T de la
crisis queda determinado por la siguiente expresión:
T=
( µτ − α ( E' − E ))e −ατ 7 β
µ( 1 − e
−ατ / β
)
39
+
αE − D0 − R β
−
µ
α
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
De esta ecuación se deduce que el momento T es una función decreciente del tipo de
cambio que se fije tras la devaluación ( E' ), es decir, cuanto mayor es la devaluación esperada,
antes se produce el ataque especulativo contra la moneda. Por otra parte, a medida que τ → 0,
T→- ∞, por tanto si el período de transición es lo suficientemente corto, el momento T tendrá
lugar en el momento 0. En concreto, si se sabe que la autoridad monetaria va a devaluar la moneda
en el momento en que se produce el ataque especulativo (es decir, τ = 0), la fuga de capitales se
producirá tan pronto como los agentes perciban que se va a producir una crisis.
La evolución del tipo de cambio durante el período de transición es diferente según sea la
duración de dicho período: para períodos de transición lo suficientemente largos, el tipo de cambio
se irá depreciando hasta que en un momento determinado se apreciará fijándose un nuevo tipo de
cambio fijo. Cuando el período de transición es corto, el tipo de cambio se irá depreciando hasta
situarse en la nueva paridad. Dependiendo de cuál sea el caso, la entrada de nuevo del Banco
Central en el mercado de divisas supondrá una entrada de capitales o una salida de los mismos.
Tras la devaluación, la evolución de la cuenta de capital dependerá de lo realista que sea el
nuevo tipo de cambio y de la adopción por parte del gobierno de políticas macroeconómicas
restrictivas apropiadas.
40
Crisis de Balanza de Pagos y Crisis Cambiarias: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
I.1.5. Esquema típico de un modelo de primera generación
Una vez analizados los principales modelos teóricos de primera generación, se podría
hacer un resumen de las características de estos modelos:
Supuestos de partida:
•
Cumplimiento de la hipótesis de la paridad del poder adquisitivo
•
Los agentes pueden disponer de tres tipos de activos: moneda nacional, bonos nacionales y
bonos extranjeros, siendo ambos tipos de bonos sustitutivos perfectos
•
La oferta monetaria es equivalente al crédito interno más las reservas del Banco Central
•
El crédito interno crece a una tasa constante µ, por lo que las reservas decrecen a esa misma
tasa
•
Los agentes poseen expectativas perfectas
•
La demanda de dinero depende positivamente del nivel de producción y negativamente de los
tipos de interés
Dadas estas hipótesis de partida, estos modelos defienden que si la expansión del crédito
interno excede la demanda de dinero, las reservas disminuirán en la misma proporción en que
aumenta el crédito interno, hasta que llega un momento en que las reservas se agotan y se produce
una crisis de balanza de pagos que da lugar a un abandono del tipo de cambio fijo.
La causa que origina el aumento del crédito interno, es un incremento del gasto público
financiado a través de la emisión de dinero, dando lugar a una disminución de las reservas. Ante
esta situación, los agentes prevén que el tipo de cambio fijo va a ser abandonado, por lo que
deciden aumentar la proporción en su cartera de activos en moneda extranjera, disminuyendo la
proporción de activos en moneda nacional. Esto genera un ataque especulativo contra la moneda
que acaba por eliminar las reservas del Banco Central y dando lugar a una crisis de balanza de
pagos, momento tras el cual el tipo de cambio pasa a flotar libremente.
La crisis también puede venir derivada de un cambio en las expectativas de inflación, ya
que al coincidir estas con las expectativas de depreciación, genera un cambio en sus tenencias de
activos deseadas a favor de los activos en moneda extranjera.
41
ESQUEMA DE UNA CRISIS CAMBIARIA SEGÚN LOS MODELOS DE PRIMERA GENERACIÓN
El esquema de una crisis de balanza de pagos descrita por los modelos de primera generación podría representarse de la siguiente manera:
Aumento del
Aumento del
Déficit Público
Crédito Interno
DISMINUCIÓN
DE RESERVAS
Aumento del
nivel de precios
Pérdidas de
competitividad
Saldo negativo de
la balanza por
cuenta corriente
ATAQUE
ESPECULATIVO:
Agotamientos de
las reservas
CRISIS
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
I.2. MODELOS EMPÍRICOS DE PRIMERA GENERACIÓN
Aunque la literatura existente sobre modelos teóricos de crisis financieras es amplia, los
trabajos empíricos desarrollados en la línea de desarrollar modelos económicos que permitan
predecir o anticipar una crisis financiera partiendo de las teorías derivadas de los modelos de
primera generación, podrían ser calificados de escasos, tal y como señalan algunos autores como
por ejemplo Blanco y Garber (1986).
Sin embargo, sí es común encontrar trabajos de carácter descriptivo cuya finalidad es
analizar el comportamiento de un conjunto amplio de variables económicas, con el objeto de
conocer qué variables se comportan especialmente distintas en los períodos anteriores a una crisis
frente al comportamiento de las mismas variables en los períodos que podrían ser denominados
como de “calma”. En este sentido, destacan de manera especial los trabajos desarrollados por
Edwards y Montiel (1989), y Edwards (1989).
En este apartado se presentan dos modelos empíricos que podrían ser calificados como de
primera generación, aunque cada uno de ellos desarrolla de manera paralela a la aplicación
práctica un modelo teórico. Adicionalmente, aunque no puede ser calificado estrictamente como
de primera generación, se presenta también el trabajo realizado por Graciela Kaminsky, Saul
Lizondo y Carmen Reinhart en 1998, dado su enorme interés entre los trabajos empíricos sobre la
detección de crisis financieras.
El primer modelo que se expone, realizado por Blanco y Garber (1986), parte de la
hipótesis de un país que mantiene un sistema de tipos de cambio fijos, en el que se produce un
agotamiento de las reservas, provocando que el tipo de cambio ya no sea viable, por lo que a partir
de ese momento el tipo de cambio comienza a flotar libremente hasta que es fijado de nuevo un
tipo de cambio fijo mayor que el inicial. Su aplicación consiste en el cálculo de los tipos de
cambios flotantes, así como las probabilidades de devaluación asociadas a cada uno de ellos. La
hipótesis de la que parten estos autores, es que si la política prioritaria del gobierno es la fiscal, y
éste utiliza el crédito interno para financiar su déficit, llega un momento en que el crédito interno
alcanza un nivel, que al gobierno le resulta imposible mantener la paridad fija. El modelo que
plantean estos autores es aplicado al caso del peso mexicano obteniéndose muy buenos resultados
a período histórico, ya que las probabilidades de devaluación son especialmente más elevadas
43
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
justo antes de que éstas se produzcan, y consigue reproducir bastante bien las devaluaciones más
importantes registradas en México durante el período analizado.
El segundo modelo analizado, es el realizado por Edwards y Montiel (1989), en el cual se
analizan un total de 20 crisis financieras ocurridas en 16 países que han sufrido una devaluación de
al menos el 15%, tras haber mantenido un régimen de tipo de cambio fijo respecto al dólar durante
al menos dos años. Edwards y Montiel analizan el comportamiento de un conjunto de variables
durante los tres períodos anteriores a la crisis, comparando los resultados con un grupo de control
constituido por países que durante un mínimo de 10 años han mantenido un régimen de tipo de
cambio fijo. Las variables que analizan son: crédito interno, déficit público, tipo de cambio
efectivo real, Balanza por cuenta corriente, Reservas/ M2, prima del mercado negro y salarios
reales. Estos autores sostienen que la crisis cambiaria puede venir provocada tanto por políticas
macroeconómicas no adecuadas, como por shocks derivados del comercio exterior.
En el trabajo realizado por Kaminsky, Lizondo y Reinhart (1998), se realiza una profunda
revisión de los modelos sobre crisis cambiarias, tanto teóricos como empíricos, de primera y de
segunda generación, proponiendo adicionalmente un método cuyo objetivo es servir de alarma
ante una posible crisis financiera a través de un amplio conjunto de indicadores económicos.
A continuación se presentan de manera individual cada uno de estos modelos.
II.2.1. Devaluaciones sucesivas y ataques especulativos sobre el peso mexicano. Herminio
Blanco & Peter M. Garber (1986)
Herminio Blanco y Peter Garber desarrollan un método empírico a partir de la literatura
existente sobre crisis de balanza de pagos, con el objetivo de cuantificar la magnitud de una
posible futura devaluación de una moneda bajo un sistema de tipos de cambio fijos derivado de un
ataque especulativo sobre la divisa.
La aplicación del modelo se desarrolla sobre el caso del peso mexicano durante el período
1973-1982, a partir de la estimación de series sobre la probabilidad de devaluación de la moneda
44
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
un período antes, el valor esperado para el nuevo tipo de cambio fijo tras la devaluación, así como
la varianza y los intervalos de confianza 5 para cada uno de los tipos de cambios.
El supuesto del que parten es que una economía puede mantener un régimen de tipo de
cambio fijo controlando la creación de crédito interno, pero si la política cambiaria no es el
principal objetivo del gobierno, sino que el cumplimiento de la misma se encuentra subordinado al
cumplimiento de otras políticas, acabarán produciéndose repetidas devaluaciones de la moneda. La
hipótesis de partida del trabajo desarrollado por Blanco y Garber, es que si la política prioritaria
del gobierno es la fiscal y éste utiliza la creación de crédito interno para financiar su déficit, el
crédito interno alcanzará un determinado nivel que hará que sea imposible mantener el tipo de
cambio fijo, siendo por tanto abandonado.
El modelo desarrollado está estructurado en tres bloques fundamentales: la demanda de
dinero, la política de devaluación, y la creación de crédito interno.
El principal componente del modelo es el mercado de dinero, el cual queda definido por
la siguiente expresión:
mt − pt = β + Ωy t − αit + wt
(1)
donde mt , pt , e yt son los logaritmos del stock de dinero, el nivel de precios interno, y el nivel de
producción respectivamente, it es el tipo de interés y wt es la perturbación aleatoria de la demanda
de dinero. β, Ω, y α son parámetros a estimar. Además, determinan que el tipo de interés interno
depende del tipo de interés extranjero y del tipo de cambio nominal, y que el nivel de precios es
función del nivel de precios extranjeros y de los tipos de cambio nominal y real:
it = it* + Eet + 1 − et
(2)
p t = p *t + et + ut
(3)
siendo i* y p* el tipo de interés y el nivel de precios extranjeros, y et y u t los logaritmos del tipo de
cambio nominal y real respectivamente. El operador E representa las expectativas de los agentes
derivadas de la información disponible a lo largo del tiempo.
5
Nivel de significación = 5%
45
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El comportamiento de las reservas netas viene determinado por cambios en las variables
determinantes de la demanda de dinero (ecuación 1) o variaciones del crédito interno. Dado el tipo
de cambio fijo e , el Banco Central deja de intervenir el mercado de divisas cuando las reservas
alcanzan el nivel crítico R expresado en moneda extranjera. Si esto se produce en el momento t, y
el Banco Central no varía su política, se establecerá un nuevo tipo de cambio fijo ( êt ), el cual será
función de las variables estocásticas del modelo. Mientras sea viable el tipo de cambio fijo inicial,
êt será un “tipo de cambio sombra” no observable por el investigador, y sólo podrá ser conocido
en el momento en que se produce la devaluación. Antes de que el nuevo tipo de cambio sea fijado,
hay un período en el que el tipo de cambio fluctúa libremente. Para que el nuevo tipo êt sea
viable, será necesario que sea mayor o igual que el tipo de cambio flexible que prevalece tras el
ataque especulativo.
Esto es así, porque cuando el Banco Central no interviene el mercado de divisas, las
reservas netas permanecen en el nivel mínimo R , y el equilibrio del mercado de dinero viene
determinado por el tipo de cambio flexible. Sin embargo, si el Banco Central se ve obligado a
devaluar e intenta establecer de nuevo un tipo de cambio fijo por debajo del tipo de cambio
flotante asociado con el nivel de reservas R , esta situación conduciría a una demanda de reservas
que el Banco Central no podría atender porque éstas ya habrían alcanzado su nivel mínimo R . Por
tanto, el nuevo tipo de cambio fijo ( êt ) deberá ser mayor que el tipo de cambio flexible que
determina el equilibrio del mercado tras el ataque contra la divisa.
Se asume la hipótesis de que el gobierno no abandona el tipo de cambio fijo hasta que las
reservas no alcancen su nivel mínimo ( R ).
Por otra parte, se asume también la hip ótesis de que el nuevo tipo de cambio fijo sigue una
función lineal simple del tipo de cambio fluctuante:
eˆt = ~
et + δvt
(4)
donde δ es un parámetro positivo, ~
et es el tipo de cambio flexible y êt es el nuevo tipo de cambio
fijo si el nivel de reservas del Banco Central alcanza el valor R en el momento t. A través de esta
última expresión (ecuación 4), se demuestra que tras un ataque especulativo el Banco Central fijará
46
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
un nuevo tipo igual al mínimo valor viable más una cantidad positiva que dependerá de la
magnitud de la fuerza que forzó el colapso del régimen.
La última parte del modelo desarrollado por Blanco y Garber para predecir las crisis
financieras del peso mexicano, se basa en la estimación de las probabilidades de crisis asociadas a
cada uno de los tipos de cambio flotantes determinados previamente. Estas probabilidades
permiten calcular las expectativas de los agentes sobre futuros tipos de cambio, a través de la
media del tipo de cambio actual y del tipo de cambio potencial en el caso de una devaluación,
ponderándolos ambos por sus respectivas probabilidades de ocurrencia.
Aplicación del modelo al peso mexicano y resultados obtenidos:
A partir de 1973 el Banco de México se convirtió en la mayor fuente de financiación del
sector público, lo que le condujo al país a una serie de sucesivas crisis de balanza de pagos, dando
lugar a que el Banco tuviera que devaluar el peso en varias ocasiones, produciéndose las más
importantes en agosto de 1976, y en febrero y agosto de 1982.
Blanco y Garber aplicaron el modelo teórico expuesto anteriormente al caso mexicano
utilizando datos trimestrales desde el cuarto trimestre de 1973 hasta el cuarto trimestre de 1981.
El procedimiento seguido por estos autores parte de la estimación en primer lugar de los
parámetros de la demanda de dinero a través de la ecuación 1. A continuación estiman a través de
un procedimiento iterativo el valor límite de las reservas (R ) y el valor del parámetro δ. Por
último estiman las expectativas de los agentes sobre los tipos de cambio futuros. De esta forma el
tipo de cambio del peso respecto al dólar (f t ) queda determinado por la siguiente expresión, donde
∈t es una perturbación aleatoria:
f t = Eet +1 + ∈t
(5)
Los resultados de los parámetros estimados por Blanco y Garber son los que se muestran a
continuación:
47
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Parámetro
Ω
Valor estimado
1,196
Desviación típica
0,051
α
Q (15)
1,310
27,021
0,627
-
R2
0,962
-
R
δ
-3.018,068
657,942
1,956
0,547
Los resultados derivados de la estimación de las probabilidades de devaluación en el
período anterior, demostraron que las probabilidades de devaluación son relativamente bajas hasta
el segundo trimestre de 1975, a partir de este momento la probabilidad de devaluación comienza a
aumentar alcanzando el valor 0,188 en el segundo semestre de 1976, justo un trimestre antes de la
devaluación de agosto de 1976. A partir del tercer trimestre de 1976 la probabilidad de
devaluación vuelve a disminuir hasta el cuarto trimestre de 1978. A partir de ese momento las
probabilidades comienzan a aumentar, alcanzando los mayores valores durante los tres trimestres
anteriores a la devaluación de febrero de 1982, e incluso después de esta devaluación de casi el
100%, la probabilidad de devaluación alcanzó su valor máximo (0,294) en el primer trimestre de
1982, cuatro meses antes de la devaluación de agosto de 1982.
En la siguiente tabla se muestran los principales resultados derivados del tipo de cambio
observado y estimado así como sus correspondientes intervalos de confianza:
Período
Tipo de
Cambio
Observado
Tipo de
Cambio
Estimado
Intervalo de
Confianza
Limite
Inferior
Intervalo de
Confianza
Limite
Superior
Desviación
Típica
1976:1
1976:2
1976:3
1976:4
1981:1
1981:2
1981:3
1981:4
1982:1
1982:2
1982:3
12,500
12,500
19,880
20,200
23,610
24,340
25,055
25,980
45,300
47,651
-
17,403
17,429
17,775
28,544
31,769
32,526
34,268
36,150
37,013
68,078
67,896
12,165
12,096
14,807
20,152
22,873
23,321
23,919
25,088
29,537
46,361
54,724
22,641
22,763
20,743
36,937
40,665
41,731
44,617
47,211
44,490
89,790
81,068
3,976
4,032
4,788
8,204
6,226
6,789
8,557
10,726
10,080
25,520
18,511
48
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Tal y como muestran los datos, las devaluaciones se producen cuando el tipo de cambio
esperado es superior al tipo de cambio fijo. Además las probabilidades de devaluación alcanzan
valores relativamente altos antes de que se produzcan las devaluaciones reales, dos de las cuales se
produjeron fuera del período muestral.
Pese a los buenos resultados obtenidos por Blanco y Garber en el sentido de la capacidad
del modelo para reproducir la historia cambiaria del peso, estos autores insisten en la necesidad de
mejorar la especificación de las distintas funciones empleadas, así como en los procedimientos de
estimación empleados.
II.2.2. Crisis de devaluación y las consecuencias macroeconómicas del proceso de ajuste
posterior sobre los países en desarrollo. Sebastian Edwards y Peter J. Montiel (1989)6
Edwards y Montiel desarrollan un modelo a través del cual analizan las 20 mayores crisis
de devaluación ocurridas en un conjunto de 16 países. Dicho modelo pretende recoger las
características fundamentales de las crisis cambiarias, así como el proceso de ajuste
macroeconómico que se produce posteriormente. Basan su análisis tanto en los efectos derivados
de una política de crédito y fiscal demasiado expansiva, así como en los shocks externos
provocados por variaciones negativas en el comercio.
Su trabajo parte del análisis del comportamiento de las siguientes variables:
−
Tipos de cambio efectivo reales
−
Balanza por cuenta corriente
−
Posición de los activos financieros en el sistema monetario
−
Prima del mercado negro de divisas (“black market premium”)
−
Los salarios reales
Todos los países analizados en este trabajo sufrieron una devaluación de sus monedas de al
menos el 15%, después de haber mantenido oficialmente un tipo de cambio fijo respecto al dólar
estadounidense durante dos o más años. En 13 de las devaluaciones analizadas, los países
6
Sebastian Edwards y Peter J. Montiel. "Devaluation crisis and the macroeconomic consequences of postponed
adjustment in developing countries". IMF Staff Pap ers. Vol. 36. No. 4 (Diciembre 1989)
49
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
correspondientes intentaron establecer de nuevo una paridad fija respecto al dólar, sin éxito en la
mayoría de los casos, y dando lugar a devaluaciones sucesivas. En los otros 7 casos, tras la
devaluación se estableció un tipo de cambio deslizante (crawling exchange rate ). Al contrario de
las teorías tradicionales sobre crisis financieras, Krugman (1979), Flood y Garber (1984), y
Obstfeld (1984), estos autores señalan cómo en todos los casos, tras la devaluación de la moneda,
se adopta algún tipo de régimen cambiario predeterminado, ya sea tipo de cambio fijo o deslizante,
y no un tipo de cambio flotante. Esta es la principal aportación del trabajo de Edwards y Montiel,
al incluir en su modelo esta característica sobre el tipo de cambio tras la crisis.
Otro de los aspectos analizados por estos autores y no incluido en los modelos
tradicionales, es la existencia de un mercado negro de divisas en los períodos cercanos a las crisis.
En la siguiente tabla se muestran los países incluidos en el estudio divididos entre aquellos
que tras la devaluación adoptaron una nueva paridad fija, y aquellos que tras la devaluación
adoptaron un régimen de tipo de cambio deslizante. En la tabla se muestran las cuantías de las
devaluaciones así como las variaciones del tipo de cambio a lo largo de los tres años posteriores:
País
Año de
devaluación
Variación del
TC un año
después
%
Devaluación
Variación del
TC dos años
después
Variación del
TC tres años
después
Países que establecieron una nueva paridad tras la devaluación
Costa Rica
1962
1965
1974
34,3
50,0
28,8
0,0
0,0
0,0
0,0
16,7
0,0
50,0
7,1
0,0
Chipre
1967
16,6
0,0
0,0
0,0
Guyana
1967
15,9
0,9
0,6
0,2
India
1966
58,6
-0,3
1,0
-0,9
Israel
Nicaragua
1962
1967
1971
1979
66,6
16,6
20,0
43,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,0
7,1
0,0
Pakistán
1972
130,1
-10,2
0,0
0,0
Sri Lanka
1967
24,1
0,0
0,5
0,0
Yugoslavia
1965
66,6
0,0
0,0
0,0
Colombia
50
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
País
Año de
devaluación
Variación del
TC un año
después
%
Devaluación
Variación del
TC dos años
después
Variación del
TC tres años
después
Países que establecieron un régimen de tipo de cambio deslizante tras la devaluación
Chile
1982
88,2
19,2
46,5
43,3
Colombia
1967
16,7
7,1
5,7
6,9
Kenya
1981
35,9
23,7
8,4
14,3
Corea del Sur
1980
36,3
6,1
6,9
6,2
México
1976
1982
1982
59,6
267,8
29,6
13,9
49,1
5,1
-0,0
-33,7
13,7
0,3
93,0
4,0
Pakistán
Fuente: Fondo Monetario Internacional (International Financial Statistics)
En el estudio realizado comienzan analizando el comportamiento del crédito interno y la
política fiscal durante los tres períodos inmediatamente anteriores a las crisis. Los resultados
obtenidos fueron comparados con un grupo de control7 constituido por países que durante 10 años
o más han mantenido un tipo de cambio fijo. Los indicadores analizados fueron:
−
Crecimiento anual del crédito interno (%)
−
Crecimiento anual del crédito interno al sector público (%)
−
Crédito interno al sector público sobre el crédito interno total (ratio x 100)
−
Déficit Fiscal (% PIB)
−
Crecimiento del crédito interno al sector público en proporción al PIB (%)
Del análisis de estas variables obtuvieron las siguientes conclusiones:
•
La política fiscal es más expansiva en el período inmediatamente anterior a la devaluación de
la moneda.
•
Los países en los que se produce la devaluación se comportan de una manera
significativamente distinta de los países integrantes del grupo de control, y especialmente en
lo que se refiere a los indicadores fiscales. Por ejemplo, durante el año anterior a la crisis, la
mitad de los países que sufrieron una devaluación dedicaron más del 25% del crédito interno
7
Los países incluidos en el grupo de control fueron: Côte d’Ivoire, República Dominicana, Ecuador, Egipto, El
Salvador, Egipto, Etiopía, Grecia, Guatemala, Honduras, República Islámica de Irán, Iraq, Jordania, Malasia, México,
Nicaragua, Nigeria, Panamá, Paraguay, Singapur, Sudán, Tailandia, Túnez, Venezuela y Zambia.
51
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
total a la financiación del sector público, mientras que en el caso de los países del grupo de
control la mediana casi no llega al 10%.
Edwards y Montiel señalan además que las dificultades de balanza de pagos no sólo son
consecuencia de políticas macroeconómicas inconsistentes, ya que en muchas ocasiones se
producen shocks externos que provocan importantes déficit por cuenta corriente. En el trabajo que
desarrollan, observan en muchos de los casos analizados que en el período anterior a la crisis
existen importantes cambios en su comercio exterior. En 6 de las 16 devaluaciones analizadas se
produjeron importantes pérdidas comerciales en el período anterior al momento del colapso del
tipo de cambio. Por este motivo, el modelo desarrollado por estos autores trata de incluir también
estos shocks externos derivados del comercio.
En la gran mayoría de las 20 devaluaciones analizadas el sector exterior experimentó un
importante deterioro en el período anterior a la crisis:
−
Coincidiendo con los modelos tradicionales de crisis cambiarias desarrollados por Krugman
(1979) y otros autores, en los cuales la devaluación tenía lugar cuando el nivel de reservas
internacionales alcanzaba un determinado valor mínimo, en 16 de los 20 casos estudiados, el
ratio de los activos extranjeros netos sobre la masa monetaria experimentó una caída a lo largo
de los dos períodos anteriores a la crisis.
−
En 14 de las 20 crisis analizadas, la Balanza por Cuenta Corriente sobre el PIB experimentó
una pérdida durante los dos períodos anteriores a la crisis, siendo especialmente importante en
Kenia en 1981 e Israel en 1971.
−
En 15 de los 19 casos para los que existía disponibilidad de datos, el tipo de cambio efectivo
real bilateral experimentó una apreciación real durante los tres períodos anteriores a la crisis, y
en 13 de estas 19 devaluaciones, la depreciación real afectó también al tipo de cambio efectivo
real multilateral en el período anterior a la crisis. La apreciación real media fue del 9,2% y del
9,0% para el tipo de cambio efectivo real bilateral y multilateral respectivamente. Ellos
señalan que estas apreciaciones fueron el resultado de incrementos en la tasa de inflación
interna de los países analizados. Comparando con el grupo de control observan que a medida
que el momento de la crisis se acerca, se incrementan las diferencias entre las tasas de
inflación de los países que han sufrido una devaluación, y los países del grupo de control. Para
estos autores esta característica es fundamental en el desarrollo de su modelo, y les permite
52
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
decir que al menos las decisiones sobre una devaluación están condicionadas por el nivel de
reservas y el tipo de cambio efectivo real.
Otra de las características del modelo desarrollado por Edwards y Montiel y no recogida
por otros modelos, es que tras la devaluación, el ratio de los activos extranjeros sobre la masa
monetaria vuelve al nivel de reservas anterior a la crisis, lo que significa que los países intentan
alcanzar siempre un nivel de reservas predeterminado.
Respecto a la prima del mercado negro de divisas (“black market premium”), observan que
en 13 de las 18 devaluaciones de las que disponen de datos, el valor de la prima del mercado negro
era mayor un mes antes que nueve meses antes de la devaluación. Observan también, que en todos
los países, inmediatamente después de la crisis se produce una caída de la prima del mercado
negro.
La última variable analizada son los salarios reales. El motivo por el cual deciden analizar
esta variable, es porque existe una creencia generalizada de que tras una devaluación se produce
un incremento de los salarios reales. En su estudio observan que en los períodos cercanos a las
crisis, en 13 países de los 18 analizados, se produjo un aumento de los salarios en el período
anterior a la crisis. Sin embargo, estos incrementos sólo fueron especialmente importantes en 7 de
los países, pero en todos ellos, tras la devaluación los salarios reales volvieron a caer. En los otros
10 casos sin embargo, los salarios reales no descendieron tras la crisis.
Conclusiones:
Tras analizar las características de las crisis de balanza de pagos en 16 países en
desarrollo, señalan que las características comunes a estas crisis son:
•
Aceleración de la tasa de inflación
•
Apreciación continua del tipo de cambio efectivo real
•
Aumento del déficit por cuenta corriente
•
Caída continuada de las reservas de moneda extranjera
•
Aumento continuo de la prima en el mercado negro de divisas
La consecuencia inmediata a una crisis, es el establecimiento de programas de ajuste
macroeconómicos, los cuales incluyen sustanciales devaluaciones del tipo de cambio.
53
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El trabajo desarrollado por Edwards y Montiel parte de una economía hipotética
caracterizada por los siguientes rasgos:
−
Una economía productora de tres bienes
−
Los agentes mantienen moneda interna y moneda extranjera y existe un tipo de cambio
bilateral
−
El Banco Central posee un nivel objetivo de reservas bien definido
Edwards y Montiel analizan la reacción de la economía frente a dos tipos de shocks:
−
Un incremento del gasto público financiado con creación de crédito interno
−
Un shock negativo sobre el comercio exterior del país
Demuestran que el programa de ajuste posterior depende del tipo de shock que ha
ocasionado la crisis:
•
Si la crisis se debe a una política fiscal demasiado expansiva, el programa de ajuste requerirá
una devaluación mayor de la moneda, aunque la relación entre la cuantía de la devaluación y
el momento en que esta se produce no es lineal. Por otra parte, cuanto más se retrase el
programa de ajuste, más se alejarán las variables endógenas de su nivel de equilibrio. Una vez
que el programa de ajuste se ha implementado, las variables macroeconómicas sobrepasarán
su nivel de equilibrio, y la diferencia será mayor cuanto más tiempo se tarde en establecer el
programa de ajuste.
•
Si la crisis se debe a un shock derivado del comercio exterior, la cuantía de la devaluación no
vendrá afectada por el tiempo que se tarde en establecer el programa de estabilización.
Además, cuanto más tiempo se retrase el ajuste, menor será la desviación de las variables
macroeconómicas respecto de su nivel inicial de equilibrio, a excepción de las reservas y la
base monetaria.
Por último, una de las conclusiones más importantes del trabajo realizado por Edwards y
Montiel, es que en muchos de los países en desarrollo, las crisis con devaluación son el resultado
de un fallo en la aplicación de medidas correctivas ante un desajuste interno o externo.
54
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.2.3. Indicadores de alerta de crisis cambiarias 8 . Graciela Kaminsky, Saul Lizondo &
Carmen Reinhart. (1998)
Estos autores realizan un estudio tanto teórico como práctico sobre las crisis cambiarias.
Su análisis parte de una revisión de la literatura teórica sobre crisis cambiarias, analizando desde
los “modelos de primera generación” iniciados por Krugman (1979), hasta los estudios más
recientes denominados comúnmente como “modelos de segunda generación”. Estos últimos, como
ya se ha mencionado en ocasiones anteriores, consideran que las crisis cambiarias pueden ser
autogeneradas (self-fulfilling), en lugar de justificar las crisis como la consecuencia de unos
fundamentos económicos débiles, argumento defendido por los modelos de primera generación.
La parte fundamental de su estudio es una recopilación de los trabajos empíricos sobre
crisis cambiarias más relevantes, con el objeto de conocer cuáles son los indicadores económicos
más utilizados y con mayor utilidad predictiva, de cara a la previsión de una posible crisis
cambiaria.
Por último, desarrollan un sistema de alarma a partir de una selección de indicadores, que
ante ciertos valores límite de esos indicadores, alerta de la posibilidad de una crisis cambiaria
durante los 24 meses siguientes al momento en el cual se supera el límite.
En cuanto a los trabajos empíricos analizados por estos autores, son clasificados en cuatro
bloques según la metodología empleada:
•
Grupo1:
Trabajos sobre los aspectos cualitativ os que provocan una crisis cambiaria.
Aunque estos trabajos sí ofrecen indicadores cuyo comportamiento debe ser
analizado para poder anticipar una crisis, no se aplican test que permitan
validar la capacidad predictiva de los indicadores.
•
Grupo2:
Trabajos que analizan las características de los períodos inmediatamente
anteriores y posteriores a las crisis. En algunos casos se compara el
comportamiento de determinadas variables en períodos considerados de
calma frente al comportamiento de las mismas en los períodos de crisis. A
veces se utiliza para realizar la comparación un grupo de control formado por
países en los cuales no se ha producido una crisis cambiaria. En este caso se
encuentran trabajos que aplican tanto tests paramétricos como no
paramétricos.
8
Título original: “Leading indicators of Currency Crisis”
55
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
•
Grupo 3:
Trabajos cuyo objetivo es determinar la probabilidad de una devaluación de la
moneda uno varios períodos antes de que ésta se produzca. Entre estos
trabajos destaca de manera especial el desarrollado por Blanco y Garber
(1986) y aplicado al caso del peso mexicano, el cual ya ha sido analizado en
detalle en el apartado I.2.1. Estos trabajos incluyen estudios individuales por
países, así como estudios multipaís.
•
Grupo 4:
En este grupo se encuentra el trabajo realizado por Kaminsky y Reinhart
(1996), en el que desarrollan un sistema no paramétrico para evaluar la
capacidad de un conjunto de variables para anticipar una crisis cambiaria.
Este trabajo es una extensión de los estudios en los que se analizan la
evolución de indicadores de alerta durante los períodos anteriores a la crisis
utilizando un grupo de control para comparar los resultados.
Los indicadores de alerta más importantes derivados de la revisión de trabajos empíricos,
con sus correspondientes transformaciones, se presentan agrupados en las siguientes categorías:
•
Cuenta de Capital:
−
−
−
−
−
Reservas internacionales
Flujos de capital
Flujos de capital a corto plazo
Inversión directa extranjera
Diferencial de tipos de interés (nacional − extranjero)
•
Deuda:
−
−
−
−
−
Deuda pública extranjera
Deuda extranjera total
Deuda a corto plazo
Deuda clasificada por tipo de prestamista y estructura
del tipo de interés
Ayuda extranjera
−
−
−
−
−
−
−
−
−
Tipo de cambio efectivo real
Balanza por Cuenta Corriente
Balanza comercial
Exportaciones
Importaciones
Términos de comercio
Precio de las exportaciones
Ahorro
Inversión
•
Cuenta Corriente:
56
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
•
Variables internacionales: −
−
−
Crecimiento real del PIB extranjero
Tipos de interés extranjeros
Nivel de precios extranjero
•
Liberalización Financiera: −
−
−
−
Crecimiento del crédito
Variaciones en el multiplicador monetario
Tipos de interés reales
Diferencia entre los tipos de interés de préstamo y
depósito
•
Otras variables
financieras:
−
−
−
−
−
−
−
−
−
−
Crédito del Banco Central al sistema bancario
Diferencia entre la oferta y la demanda de dinero
Crecimiento del dinero
Rendimiento de los bonos
Inflación nacional
Tipo de cambio sombra
Prima del mercado de cambio paralelo
Paridad central del tipo de cambio
Posición del tipo de cambio respecto a la banda oficial
Ratio M2/Reservas internacionales
•
Sector Real:
−
−
−
−
−
−
Crecimiento real del PIB
Producción
PIB potenciasl (output gap)
Nivel de empleo, desempleo
Salarios
Variación de existencias
•
Variables fiscales:
•
Factores estructurales:
−
−
−
−
−
−
−
−
−
−
−
Déficit fiscal
Consumo público
Crédito al sector público
Grado de apertura
Concentración comercial
Controles de cambio
Duración de los períodos de sistema de tipo de cambio
fijo
Liberalización financiera
Crisis bancarias
Crisis cambiarias pasadas
Acontecimientos pasados sobre el mercado de divisas
−
−
Inconveniente victoria o pérdida ele ctoral
Cambio de gobierno
•
Variables políticas:
57
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
A partir de todo este conjunto de indicadores, Kaminsky, Lizondo y Reinhart analizan
cuáles de ellos poseen mayor capacidad predictiva en la anticipación de una crisis cambiaria. El
punto de partida es escoger aquellos indicadores que resultaron estadísticamente significativos en
los trabajos originales de los distintos autores que los realizaron.
Partiendo de este modo de una primera selección de indicadores, Kaminsky, Lizondo y
Reinhart, seleccionan para el caso de los trabajos empíricos basados en la comparación de los
indicadores respecto a un grupo de control, aquellos en los que las diferencias resultan
estadísticamente significativas; y para el caso de los trabajos empíricos que estiman la
probabilidad de crisis un período o varios antes de que esta se produzca, realizan regresiones
individuales tipo logit o probit. En ambos casos el nivel de significación exigido es al menos del
10%. De este modo, las variables que muestran mayor capacidad predictiva en la anticipación de
una crisis cambiaria son las siguientes:
−
Tipo de cambio efectivo real
−
Crisis bancarias
−
Exportaciones
−
Variación de existencias
−
Ratio M2/ Reservas internacionales
−
Producción
−
Exceso de saldos de M1
−
Reservas internacionales
−
Multiplicador de la M2
−
Ratio Crédito interno/ M2
−
Tipo de interés real
−
Términos de comercio (valor unitario de las exportaciones sobre valor unitario de las
importaciones)
−
Diferencial de tipos de interés reales
−
Importaciones
−
Depósitos bancarios
−
Ratio tipo de interés de préstamo/ tipo de interés de depósito
A partir de esta batería de indicadores, Kaminsky, Lizondo y Reinhart desarrollan un
sistema de alarma alternativo con el fin de poder predecir una crisis cambiaria con la suficiente
antelación como para que el gobierno pueda tomar medidas económicas para evitarla.
58
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El método propuesto estima la probabilidad de una crisis condicionada a las señales de
alarma emitidas por los indicadores en función de su capacidad predictiva, de tal forma que la
probabilidad de crisis será mayor si las señales provienen de indicadores con gran capacidad de
predicción que si provienen de indicadores cuya utilidad en la anticipación de una crisis es más
escasa.
En la siguiente tabla se recogen las características de la aplicación realizada por estos
autores:
•
Población y período
muestral
15 países en desarrollo y 5 países industriales
Datos mensuales desde 1970 - 1995
76 períodos de crisis
•
Definición de crisis
Ataque sobre una moneda que produce una depreciación de
la misma o una importante caída de las reservas
internacionales, o ambas situaciones a la vez. Para cada país
se identifican las crisis a partir de un “índice de presión
sobre el mercado de divisas”, el cual es una media
ponderada de las variaciones mensuales del tipo de cambio
respecto al USD o al marco alemán, y de las variaciones
mensuales de nivel de reservas extranjeras. Cuando el valor
del índice supera la media más tres veces la desviación
típica, se dice que hay una crisis.
•
Señales de alarma
Una señal de alarma seguida por una crisis en los 24 meses
siguientes, es considerada una “buena señal”, mientras que
una señal no seguida por una crisis en este período es
considerada como una “señal falsa o ruido”.
•
Límites para establecer
señales de alarma
Cuando el valor de un indicador en un determinado período
supera el valor del percentil 10 ó 20. Esto se realiza para
cada uno de los indicadores y en cada uno de los países.
De cara a conocer la capacidad predictiva de cada uno de los indicadores de manera
individual, construyen la siguiente tabla de contingencia para cada uno de los indicadores
analizados:
59
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Crisis
No crisis
Señales de alarma emitidas
A
B
No señales de alarma
C
D
Donde A es el número de meses para los cuales el indicador ha emitido una buena señal, B
es el número de meses para los cuales el indicador emitió una señal falsa, C es el número de meses
en los cuales el indicador debía haber emitido una señal de alarma y no lo hizo, y D es el número
de meses en los que el indicador acertó no emitiendo ninguna señal de alarma ya que no se produjo
ninguna crisis. De esta matriz se deriva que un indicador sería perfecto cuando C = 0 y B = 0, a la
vez que A > 0 y D > 0.
Resultados:
Los principales resultados obtenidos por estos autores se resumen en la siguiente tabla.
Nº de crisis
% de crisis
correctas
% de
buenas
señales
% de
males
señales
Señales falsas
ponderadas
(A)
A/
(A+C)
B/
(B+D)
[B/(B+D)]/
[A/(A+C)]
Tipo de cambio efectivo real
72
57
25
5
0,19
Crisis bancarias
26
37
19
6
0,34
Exportaciones
72
85
17
7
0,42
Variación de existencias
53
64
17
8
0,47
M2/ Reservas internacionales
70
80
21
10
0,48
Producción
57
77
16
8
0,52
Exceso de saldos de M1
66
61
16
8
0,52
Reservas internacionales
72
75
22
12
0,55
Multiplicador de la M2
70
73
20
12
0,61
Crédito interno/ PIB
62
56
14
9
0,62
Tipos de interés reales
44
89
15
11
0,77
Términos de comercio
58
79
19
15
0,77
Diferencial tipos interés reales
42
86
11
11
0,99
Importaciones
71
54
9
11
1,16
Depósitos bancarios
69
49
16
19
1,20
T. interés préstamo/ T. Interés
depósito
33
67
13
22
1,69
60
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
De todos estos valores, los más importantes son los correspondientes a la última columna,
la cual muestra simultáneamente la capacidad de los indicadores para emitir buenas señales, así
como para evitar ruidos. De este indicador se deduce que será mejor aquel indicador que muestre
un menor valor en esta columna (tipo de cambio efectivo real).
Por otra parte, señalan que no sólo es importante que un indicador sea capaz de emitir
buenas señales y evitar señales falsas, sino que además es importante que sea capaz de emitir
buenas señales con la suficiente anticipación como para que el gobierno pueda tomar las medidas
oportunas. Por ello, analizan también el tiempo que transcurre desde que el indicador emite una
señal de alarma hasta que se produce la crisis. La conclusión extraída de este análisis es que la
mayoría de los indicadores emiten la señal de alarma un año o año y medio antes de que la crisis se
produzca, siendo el indicador de problemas bancarios el que emite la señal con mayor anticipación
(19 meses), seguido por el tipo de cambio efectivo real (17 meses) y los tipos de interés reales (17
meses).
Las conclusiones extraídas no sólo del sistema de alarma desarrollado por estos autores
sino también de los estudios que revisan en la etapa previa, se pueden resumir en los siguientes
puntos:
•
En primer lugar, estos autores señalan que un buen sistema de alarma para la predicción de
una crisis, debe incluir un conjunto variado de indicadores, ya que las crisis se pueden
manifestar en varios sentidos.
•
Entre los indicadores que señalan como más útiles en la anticipación de una crisis cambiaria,
se encuentran el comportamientos de las reservas internacionales, el tipo de cambio efectivo
real, el crédito interno, el crédito al sector público y la inflación interna.
•
Un segundo grupo de indicadores quedaría formado por la balanza comercial, las
exportaciones, el crecimiento del dinero, el crecimiento real del PIB y el déficit fiscal.
•
Por último, advierten de que también un buen sistema de alarma está sometido a limitaciones,
ya que se pueden producir factores externos de tipo político o institucional que afecten de
manera negativa al tipo de cambio de una moneda.
61
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
I.3.
MODELOS
DE
SEGUNDA
GENERACIÓN:
CRISIS
CAMBIARIAS
AUTOGENERADAS
Frente a los primeros trabajos desarrollados sobre las causas de las crisis cambiarias y
crisis de balanza de pagos, los cuales establecen como principal causa de las mimas unos
fundamentos económicos débiles basados en políticas fiscales, monetarias y cambiarias
incompatibles entre sí, en los últimos años se han desarrollado trabajos que defienden que las
causas que han decidido a las autoridades monetarias a abandonar un sistema de tipo de cambio se
derivan de otros indicadores económicos.
Estos estudios más recientes han sido denominados en la literatura económica como
“modelos de segunda generación” y defienden que las crisis cambiarias no tienen por qué
producirse como consecuencia de unos fundamentos económicos débiles, sino que son las
expectativas de los agentes las que pueden provocar dichas crisis, incluso sin que se haya
producido una alteración de la política económica del gobierno. Se denominan crisis
“autogeneradas” (self-fulfilling), ya que se produce un círculo entre agentes y la política
económica. Los agentes se forman sus expectativas y de esta forma afectan a la actividad
económica e influyen además sobre la política económica.
Si bien el objetivo del presente trabajo es el estudio de los modelos de crisis cambiarias de
primera generación, a continuación se muestra un breve resumen de los diferentes modelos
teóricos de segunda generación. La realización de este apartado se ha basado fundamentalmente en
el trabajo de tesina realizado por Eva Medina (2000) “Modelos de segunda generación para la
determinación del tipo de cambio. Una aplicación para los países Latinoamericanos”, y por el
trabajo de Kaminsky, Lizondo y Reinhart (1998).
El primer trabajo realizado en esta línea es el modelo planteado por Maurice Obstfeld en
1994, en el que plantea que las expectativas de los agentes sobre una futura devaluación de la
moneda da lugar a un incremento de los costes salariales que se traduce en un incremento de
precios. Esta situación provoca que en un momento determinado el coste sobre la economía del
país del aumento de precios es mayor que el coste que supone para el país mantener el tipo de
cambio, por lo que finalmente el gobierno decide devaluar la moneda, haciendo de esta forma que
las expectativas de los agentes se hayan cumplido. En un trabajo posterior realizado por el mismo
autor, las expectativas sobre el abandono del tipo de cambio provocan incrementos en los tipos de
62
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
interés, haciendo que el gobierno abandone la paridad con el fin de evitar mayores costes de la
deuda pública. Obstfeld señala también que los aumentos de los tipos de interés aumentan la
posibilidad de una crisis bancaria con sus consiguientes costes fiscales.
El modelo planteado por Ozkan y Sutherland (1995) plantea como variables clave para la
previsión de una crisis cambiaria la evolución del nivel de producción, y los tipos de interés
nacionales y extranjeros. Según estos autores, la función objetivo del gobierno depende
positivamente de los beneficios derivados de mantener fijo el tipo de cambio (control de la
inflación), y negativamente de la desviación del nivel de producción respecto a un nivel objetivo.
Bajo un sistema de tipo de cambio fijo, incrementos en los tipos de interés extranjeros conducen a
incrementos del tipo de interés interno, provocando menores niveles de producción, dando lugar a
que a las autoridades les resulte muy costoso mantener la paridad de la moneda. En el momento en
que los tipos de interés extranjeros alcancen un determinado valor, el coste de mantener el tipo de
cambio fijo superará los beneficios, haciendo que las autoridades tengan que abandonar el tipo de
cambio. Además, el incremento de los tipos de interés interno supone mayores costes de
financiación para el gobierno, por tanto, dado que las autoridades son conscientes de los efectos de
su política cambiaria, la decisión de abandonar el tipo de cambio fijo o no vendrá determinada
también por el nivel de deuda pública. Por otra parte, altos tipos de interés hacen que el sistema
bancario se debilite, y ante este riesgo las autoridades prefieren devaluar la moneda.
Otros modelos defienden que las políticas macroeconómicas no están predeterminadas,
sino que responden a cambios en la situación económica y que los agentes económicos forman sus
expectativas de acuerdo a esta característica. Del mismo modo, las expectativas y las acciones de
los agentes influyen sobre determinadas variables ante las cuales las políticas económicas
responden. Este círculo da lugar a que puedan existir múltiples situaciones de equilibrio sin que se
produzcan alteraciones de los fundamentos económicos. Esto hace que una economía que se
encuentra inicialmente en equilibrio bajo un sistema de tipo de cambio fijo, ante un
empeoramiento de las expectativas, tenga que variar su política económica, dando lugar al
abandono del régimen cambiario, validando de este modo las expectativas de los agentes.
Por último, los trabajos más recientes se han basado en los efectos de contagio entre unas
economías y otras. Entre ellos destaca el trabajo desarrollado por Gerlach y Smets (1994), en el
que la devaluación de la divisa de un país conduce a devaluaciones de las monedas de sus socios
comerciales ante el temor de una pérdida de competitividad. En los modelos de contagio, una crisis
cambiaria en un país próximo es un indicador de una posible crisis cambiaria interna.
63
CAPITULO II:
MODELO PARA LA ESTIMACIÓN DEL RIESGO
CAMBIARIO EN LOS PAÍSES DE EUROPA
CENTRAL Y ORIENTAL
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.1. IMPORTANCIA Y CARACTERÍSTICAS DE LA MUESTRA
Partiendo de las conclusiones extraídas sobre las causas que provocan una crisis cambiaria,
a través de los modelos teóricos y empíricos de primera generación analizados en el capítulo II, se
ha desarrollado un modelo econométrico de corte transversal utilizando la metodología logit, con
el objeto de estimar el riesgo cambiario en un conjunto de países de Europa Central y Oriental.
Este trabajo se encuadra dentro de un conjunto de estudios sobre la estabilidad de las
monedas y la paridad del poder adquisitivo, aplicando metodología logit, probit y cointegración,
desarrollados en el área de Economía Internacional del Instituto de Predicción Económica
Lawrence R. Klein de la Universidad Autónoma de Madrid. El primero de estos trabajos se inició
con un modelo logit para la estimación del riesgo cambiario de los países latinoamericanos 9 . El
modelo que se presenta a continuación, sigue esta misma línea de trabajo en cuanto a metodología
y objetivo, aunque con una diferencia fundamental, ya que es el primer modelo empírico que
pretende reproducir los rasgos de una crisis cambiaria definidos por los modelos de primera
generación.
El motivo por el cual se han elegido los países de Europa Central y Oriental como área
geográfica de aplicación, se encuentra en el interés económico que suponen para España debido a
que bastantes de ellos se incorporarán a la Unión Europea 10 en un futuro no muy lejano, si bien un
primer grupo de estos países lo harán probablemente en el 2004, y otro segundo grupo se
incorporarán antes de finalizar el año 2012. Es cierto que aunque las relaciones comerciales entre
España y algunos de estos países (Polonia, República Checa y República Eslovaca) han aumentado
de manera importante durante los últimos cinco años, el porcentaje que representan actualmente
estas economías sobre el comercio español sigue siendo aún muy bajo. Tampoco estos países han
sido el foco de atención de la inversión de las empresas españolas. Sin embargo, estos países
poseen un alto potencial económico, reflejado en un crecimiento del PIB creciente y sostenido, en
una tendencia de reducción de la inflación y unos costes laborales sensiblemente más bajos que los
españoles, haciendo que deban ser considerados por un lado como mercados estratégicos, y por
otro unos potenciales competidores, especialmente en lo que se refiere a productos agríc olas.
9
“Modelos de crisis Financieras” (Enero 2000). Herrarte, Medina y Vicéns. Documento de trabajo 00/1. Instituto de
Predicción Económica L.R. Klein. Facultad de CC.EE. y EE. Universidad Autónoma de Madrid.
10
Hungría, Polonia, República Checa y Eslovenia tienen previsto su incorporación en el 2004, mientras que la República
Eslovaca, Bulgaria y Rumania lo harán en el 2012. Ver Vicéns Otero, José “Europa Central y Oriental. Una llamada de
atención”. Nota CEPREDE nº00.6 (May. 2000). Editado por CEPREDE.
65
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Otros países ya han detectado este potencial, ya que la inversión extranjera directa en estas
economías ha aumentado notablemente en la última década, por lo que la relación entre España y
estos países acabará siguiendo la misma tendencia, haciendo imprescindible el conocimiento de los
riesgos financieros que puedan existir.
Teniendo en cuenta la disponibilidad de datos, su calidad y su frecuencias, de todo este
bloque de países, finalmente fueron seleccionados los siguientes nueve países, de los que se
recogen sus rasgos fundamentales:
Bulgaria:
PIB (Mill. USD): 12.256,9 (1998)
PIB real (Mill. USD): 761,39 (1998)
PIB sobre total área (1998): 2,0%
% Cto. PIB real (1999): 2,4%
Tasa de paro (1999): 13,7%
Inflación (1999): 1,8%
BCC (% PIB) (1999): -5,4%
Moneda : Leva
TC leva/DM: 0,9389 (1999)
TC leva/USD: 1,8364 (1999)
PNB per cápita (USD, 1998): 1.230
Eslovenia:
PIB (Mill. USD): 19.523,9 (1998)
PIB real (Mill. USD): 15.046,0 (1998)
PIB sobre total área (1998): 3,1%
% Cto. PIB real (1999): 4,9%
Tasa de paro (1999): 13,6%
Inflación (1999): 5,9%
BCC (% PIB) (1999): -2,9%
Moneda : Tolar
TC tolar/ DM: 92,938
TC tolar/ USD: 181,77
PNB per cápita (USD, 1998): 9.760
Hungría:
PIB (Mill. USD): 47.399,7 (1998)
PIB real (Mill. USD): 29.118,2 (1998)
PIB sobre total área (1998): 7,6%
% Cto. PIB real (1999): 4,5%
Tasa de paro (1999): 9,7%
Inflación (1999): 9,1%
BCC (% PIB) (1999): -4,3%
PIB (Mill. USD): 143.131,8 (1997)
PIB real (Mill. USD): 104.851,2 (1998)
PIB sobre total área (1998): 16,9%
% Cto. PIB real (1999): 4,1%
Tasa de paro (1999): 12,0%
Inflación (1999): 6,8%
BCC (% PIB) (1999): -7,5%
Polonia:
66
Moneda: Forint
TC forint/ DM: 121,251
TC forint/ USD: 237,146
PNB per cápita (USD, 1998): 4.510
Moneda: Zloty
TC zloty/ DM: 2,028
TC zloty/ USD : 3,967
PNB pe r cápita (USD, 1998): 3.900
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
República
Checa:
República
Eslovaca :
Rumania :
Rusia :
Ucrania :
PIB (Mill. USD): 53.119,8 (1999)
PIB real (Mill. USD): 40.438,0 (1999)
PIB sobre total área (1998): 9,0%
% Cto. PIB real (1999): -0,2%
Tasa de paro (1999): 8,6%
Inflación (1999): 2,0%
BCC (% PIB) (1999): -2,0%
PIB (Mill. USD): 18.840,5 (1999)
PIB real (Mill. USD): 15.098,0 (1999)
PIB sobre total área (1998): 3,3%
% Cto. PIB real (1999): 1,9%
Tasa de paro (1999): 17,5%
Inflación (1999): 9,5%
BCC (% PIB) (1999): -5,7%
PIB (Mill. USD): 34.027,4 (1999)
PIB real (Mill. USD): 7.521,7 (1998)
PIB sobre total área (1998): 6,7%
% Cto. PIB real (1999): -3,2%
Tasa de paro (1999): 11,4%
Inflación (1999): 30,1%
BCC (% PIB) (1999): -3,8%
PIB (Mill. USD): 184.627,1 (1999)
PIB real (Mill. USD): 147.963,4 (1998)
PIB sobre total área (1998): 44,7%
% Cto. PIB real (1999): 3,2%
Tasa de paro (1999): 2,1%
Inflación (1999): 46,1%
BCC (% PIB) (1999): 11,3%
PIB (Mill. USD): 42.404,2 (1998)
PIB real (Mill. USD): 42478,9 (1997)
PIB sobre total área (1998): 6,8%
% Cto. PIB real (1999):
Tasa de paro (1999): 3,5%
Inflación (1999): 18,5%
BCC (% PIB) (1999): -3,1%
Moneda: Corona checa
TC corona/ DM: 17,675 (1999)
TC corona/ USD: 34,569 (1999)
PNB per cápita (USD, 1998): 5.040
Moneda: Corona eslovaca
TC corona/ DM: 21,149 (1999)
TC corona/ USD: 41,363 (1999)
PNB per cápita (USD, 1998): 3.700
Moneda: leu (lei)
TC leu/ DM: 7839,5 (1999)
TC leu/ USD: 15332,8 (1999)
PNB per cápita (USD, 1998): 1.390
Moneda: Rublo ruso
TC rublo/ DM: 12,6 (1999)
TC rublo/ USD: 24,6 (1999)
PNB per cápita (USD, 1998): 2.300
Moneda: Hryvnia
TC Hryvnia/ DM: 2,11 (1999)
TC Hryvnia/ USD: 4,13 (1999)
PNB per cápita (USD, 1998): 850
Fuente: Fondo Monetario Internacional (International Financial Statistics, World Economic Outlook),
OCDE (Main Economic Indicators)
La muestra analizada comprende el período desde enero de 1992 hasta junio de 2000,
utilizando datos mensuales para la mayor parte de las variables. Adicionalmente, se han utilizado
mediciones distintas para cada una de las variables incluidas (niveles, tasas de variación, ratios
sobre otra variable), con el fin de evitar la eliminación en el modelo de variables que podrían ser
fundamentales para la determinación de una crisis cambiaria.
67
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.2. DEFINICION DE PERÍODOS DE CRISIS Y PERÍODOS DE CALMA
La especificación del modelo ha partido en primer lugar de la determinación de los
“períodos de crisis” y de los “períodos de calma” para cada uno de los países, entendiendo
como períodos de crisis aquellos en los que se producen fuertes oscilaciones depreciatorias del tipo
de cambio, y períodos de calma aquellos en los que el tipo de cambio no sufre importantes
variaciones. La moneda de referencia utilizada para el cálculo de las variaciones del tipo de
cambio ha sido el marco alemán, ya que en la mayor para de los casos Alemania es el principal
socio comercial de estos países. El tipo de cambio respecto al marco alemán de cada una de las
monedas ha sido calculado a partir del tipo de cambio respecto al dólar americano, obtenido de la
publicación
mensual
“Estadísticas
Financieras
Internacionales”
del
Fondo
Monetario
Internacional11 .
En la siguiente tabla se muestran los dos principales socios comerciales para cada uno de
los países en función del porcentaje de importaciones y exportaciones:
Principales socios comerciales de los países de Europa Central y Oriental
País
Bulgaria
Eslovenia
Hungría
Polonia
República Checa
República Eslovaca
Rumania
Rusia
Ucrania 12
Importaciones 1998
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Rusia 20,1%
Alemania 14,0%
Alemania 20,7%
Italia 16,8%
Alemania 28,2%
Austria 9,6%
Alemania 19,5%
Italia 7,9%
Alemania 34,4%
Rep. Eslovaca 7,2%
Alemania 25,9%
Rep. Checa 18,5%
Alemania 17,5%
Italia 17,4%
Alemania 11,7%
Bielorrusia 10,9%
Rusia 48,1%
Unión Europea 22,7%
Exportaciones 1998
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Italia 12,8%
Alemania 10,5%
Alemania 28,4%
Italia 13,9%
Alemania 36,6%
Austria 10,6%
Alemania 36,0%
Italia 5,8%
Alemania 38,5%
Rep. Eslovaca 10,6%
Alemania 28,9%
Rep. Checa 20,3%
Italia 22,0%
Alemania 19,6%
Ucrania 9,1%
Alemania 9,0%
Rusia 23,0%
Unión Europea 16,9%
Fuente: Economist Intelligence Unit (Country Report)
11
A partir de enero de 1999 el FMI ofrece el tipo de cambio euro/dólar, por lo que se han calculado los tipos de cambio
en este periodo aplicando la paridad fija DM/euro de 1,95583.
68
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El criterio utilizado para fijar los períodos de crisis y de calma, ha sido considerar que se
produce una crisis cuando la variación mensual del tipo de cambio de la moneda de un país
respecto al marco alemán es superior al 10%. El motivo por el cual se ha elegido el 10% como
valor de referencia, ha sido porque se ha considerado que una variación mensual del tipo de
cambio superior a este límite es demasiado elevada y puede estar reflejando una crisis cambiaria
subyacente. Adicionalmente, la fijación de este valor se ha basado también en los estudios
empíricos analizados en el capítulo I.2. 13 , donde se utilizan valores de referencia para establecer
los períodos de crisis desde el 5% al 20%. En este trabajo se ha considerado el 5% una cifra
demasiado pequeña lo cual podría dar lugar a estimaciones demasiado elevadas sobre la
probabilidad de riesgo cambiario, mientras que el 20% es demasiado elevado, con lo cual el
modelo estimado no predeciría crisis que podrían tener lugar.
En la siguiente tabla se muestran las variaciones medias del tipo de cambio, así como sus
desviaciones típicas, para cada uno de los países analizados en la muestra. Como se puede
observar, aunque la variación media del tipo de cambio en ninguno de los casos es superior al
10%, la dispersión del tipo de cambio es especialmente elevada en el caso de Bulgaria, Rusia y
Ucrania. Adicionalmente, en el caso de la República Checa y la República Eslovaca, la variación
del tipo de cambio no supera para ninguno de los datos mensuales el límite establecido del 10%,
ya que los valores máximos de la variación del tipo de cambio son del 5,79% y del 7,25%
respectivamente. Sin embargo, ambos países han sido mantenidos en la muestra, como se explic ará
más adelante, debido a su importancia en la economía de este área, ya que suponen más del 10%
del total del PIB de la zona, y más del 20% si no se tiene en cuenta a Rusia en la muestra.
12
En este caso no se ha realizado un nivel de desagregación mayor por falta de disponibilidad de datos en la fuente
original.
13
Edwards y Montiel (1989): Depreciación del 15%; Herrarte, Medina y Vicéns (2000): Depreciación del 10%; Frankel
y Rose (1996): Depreciación del 25%, junto con un aumento del 10% en la tasa de depreciación respecto al año anterior;
Modelo de JP Morgan (1998): Depreciación del 10%; Kaminsky, Lizondo y Reinhart (1998) construyen un índice de
presiones especulativas a partir de la variación del tipo de cambio y las reservas.
69
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Variaciones del Tipo de cambio respecto al marco alemán
Enero 1992 – Junio 2000
País
Media
Desv. Típica
Máximo
Mínimo
Bulgaria
5,79%
24,46%
227,20%
-31,36%
Eslovenia
1,06%
2,55%
23,19%
-0,63%
Hungría
1,00%
1,77%
10,94%
-2,26%
Polonia
1,12%
2,66%
10,90%
-10,33%
Rep. Checa
0,02%
1,44%
5,79%
-4,32%
Rep. Eslovaca
0,22%
1,57%
7,25%
-2,76%
Rumania
4,65%
6,89%
41,14%
-6,68%
Rusia
6,87%
17,86%
126,10%
-8,66%
Ucrania
9,13%
21,53%
104,89%
-6,62%
Fuente: Elaboración propia a partir de datos del Fondo Monetario Internacional
(International Financial Statistics)
Siguiendo con la definición de los períodos de crisis, es necesario señalar que, en algunos
casos, un período de crisis abarca más de un mes, ya que tras el momento inicial en que el tipo de
cambio se deprecia más de un 10%, pueden sucederse variaciones del mismo superiores o
inferiores al limite fijado. Estas variaciones no deben ser consideradas como crisis independientes,
sino como una continuación de la primera depreciación de la moneda. En este sentido se considera
que un período de crisis finaliza cuando se suceden seis meses consecutivos en los que el tipo de
cambio no se deprecia más del 10% establecido, y por tanto, el final del período de crisis vendrá
marcado por el último mes en el que se ha superado el límite de depreciación.
Este es el caso por ejemplo de Rumania, país en el cual se inicia un período de crisis en
marzo de 1993 debido a una depreciación del tipo de cambio del 14,45%, y este período no
finaliza hasta marzo de 1994, ya que durante los meses intermedios el tipo de cambio fluctúa tanto
por encima como por debajo del 10%. Por último, se considera que el período de calma comienza
en octubre de 1994, ya que es en ese momento cuando han transcurrido seis meses de
“tranquilidad” respecto a las variaciones del tipo de cambio. En la siguiente tabla se muestra la
descripción de este período de crisis así como el inicio del siguiente período de calma.
70
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Abr.93-Ago.93
Menos de 6
meses de calma,
continúa la crisis
Menos de 6 meses
consecutivos de calma,
continúa la crisis
Período
Mar-93
% Tipo de cambio
Abr-93
6,31
May-93
2,29
Jun-93
7,71
Jul-93
7,52
Ago-93
6,40
Sep-93
12,43
Oct-93
Nov-93
12,13
4,50
Dic-93
6,21
Ene-94
Feb-94
19,29
8,04
Mar-94
10,07
Abr-94
3,97
May-94
1,59
Jun-94
2,39
Jul-94
4,85
Ago-94
0,51
Sep-94
3,25
Oct-94
3,70
14,45
Período de crisis
Seis meses consecutivos en
los que la depreciación del
tipo de cambio no supera
el 10%
Comienzo del período de
calma
En cuanto a los períodos de calma, un período de calma está formado por un conjunto de
meses consecutivos durante los cuales el tipo de cambio no sufre variaciones superiores al 10%.
Para delimitar aún mejor los períodos de calma, estos se han establecido sin incluir los seis meses
anteriores a una crisis (ya que se considera que es en estos meses cuando se está gestando una
crisis), y los seis meses posteriores (ya que se considera que en este período todavía pueden
permanecer los efectos de la crisis sobre la economía).
Para todos los países analizados, excepto para la República Checa y la República
Eslovaca, hay al menos un período de crisis y uno de calma. En el caso de estos dos países, la
variación del tipo de cambio no supera en ningún caso el 10%, siendo la variación máxima en la
República Checa del 5,79%, y del 7,25% en la República Eslovaca.
71
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Con el fin de no eliminar estas economías del análisis debido a su importancia dentro del
área de Europa Central y Oriental, sólo se han tomado valores de estos países para los períodos de
calma. El procedimiento seguido en este caso para determinar los períodos de calma, ha sido
buscar el valor máximo de la variación del tipo de cambio, y tomando este valor como referencia y
dejando los seis meses anteriores y posteriores, se ha calculado la media de los períodos
correspondientes para cada una de las variables analizadas. En el caso de la República Checa la
variación máxima del tipo de cambio se produce en febrero de 1999, y en la República Eslovaca
en octubre de 1998. De esta forma, los períodos de calma para estos países quedan recogidos en la
siguiente tabla:
País
Variación máxima del Tipo
de cambio
República Checa
Feb. 98
República Eslovaca
Oct. 98
Períodos de calma
•
•
•
•
Ene. 92 - Jul. 98
Sep. 99 - Jun. 00
Ene. 92 - Mar. 98
May. 99 - Jun. 00
II.3. DEFINICIÓN DE LA VARIABLE ENDÓGENA
A partir de esta definición de los períodos de crisis y de calma, se determina la variable
endógena, la cual es de carácter dicotómico, tomando valor 1 cuando se trata de un período de
crisis, y valor 0 cuando se trata de un período de calma. De esta forma quedan definidos un total de
17 períodos de crisis, y 19 períodos de calma, los cuales quedan recogidos por países en la
siguiente tabla :
72
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
País
Bulgaria
Crisis/ Calma
Período
Variación del Tipo
de cambio (%) (*)
Crisis
Mar. 94 – Sep. 94
31,49
May. 96 – Feb. 97
43,99
Ene. 92 – Ago. 93
0,80
Abr. 95 – Oct. 95
0,43
Sep. 97 – Jun. 00
0,01
Crisis
Feb. 92
23,19
Calma
Sep. 92 – Jun. 00
0,72
Crisis
Mar. 95
10,94
Calma
Ene. 92 – Ago. 94
1,09
Oct. 95 – Jun. 00
0,66
Mar. 92
10,90
Sep. 93
10,70
Oct. 92 – Feb. 93
0,52
Abr. 94 – Jun. 00
0,69
Ene. 92 – Jul. 98
-0,02
Sep. 99 – Jun. 00
-0,13
Ene. 92 – Mar. 98
0,12
May. 99 – Jun. 00
-0,42
May. 92 – Ago. 92
14,59
Mar. 93 – Mar. 94
14,45
Nov. 95
10,42
Ene. 97 – Feb. 97
28,54
Mar. 99
11,22
Oct. 94 – Abr. 95
2,84
Sep. 97 – Ago. 98
1,65
Oct. 99 – Jun. 00
1,49
Jul 92 – Jun. 95
28,52
Sep. 98 – Ene. 99
126,10
Ene. 96 – Feb. 98
0,18
Ago. 99 – Jun. 00
0,46
Ene. 93 – Dic. 93
14,07
Jun-94 – Oct. 95
26,09
Sep-98 – Oct. 98
34,02
Ago. 99
14,12
May. 96 – Feb. 98
-0,61
Mar. 00 – Jun. 00
-0,99
Calma
Eslovenia
Hungría
Crisis
Polonia
Calma
Calma
República Checa
República Eslovaca
Calma
Crisis
Rumania
Calma
Crisis
Rusia
Calma
Crisis
Ucrania
Calma
(*) En el caso de los períodos de crisis que comprenden más de un mes, el valor de la variación del tipo
de cambio se refiere al primer mes en que se produce la depreciación del tipo de cambio superior al 10%.
73
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.4. VARIABLES EXPLICATIVAS
Según la literatura teórica y empírica, se pueden extraer un conjunto de variables que
resultan buenos indicadores de cara a la predicción de una crisis cambiaria. Estas variables pueden
clasificarse en dos grupos:
1) Variables primarias
2) Variables inducidas
Las variables primarias son la causa original que actúa de motor sobre la economía
degenerando finalmente en una crisis cambiaria. Las variables inducidas son indicadores que
sufren alteraciones como consecuencia de cambios en las variables primarias. Según el esquema
presentado en el capítulo I.1.5., estas variables se agrupan de la siguiente manera:
Variables primarias
Variables inducidas
•
Déficit Público
•
Tipo de cambio efectivo real
•
Indice de precios
•
Crédito interno
•
Balanza por cuenta corriente
•
Reservas
•
Producto interior bruto
Pese a que el inicio del proceso se encuentra en las variables primarias, de cara a la
realización de un modelo empírico, es necesario tener en cuenta todo el conjunto de variables,
tanto primarias como inducidas. Dado que el objetivo último de la realización de este trabajo ha
sido construir un modelo que sirva de herramienta para la predicción del riesgo de crisis cambiario
en un conjunto de países, la selección de variables se ha realizado seleccionando aquellos
indicadores que por su capacidad predictiva, así como por la disponibilidad de datos, ofrecieran
mejores resultados. Por este motivo, el modelo que se presenta en este trabajo ha partido de un
análisis individual de todo este conjunto de variables, expresadas en la mayoría de los casos en
diferentes unidades de medida, para posteriormente realizar una selección de los indicadores que
permitan anticipar la proximidad de una crisis cambiaria.
A continuación se analiza la relación existente entre cada una de las variables explicativas
incluidas en el modelo y la probabilidad de crisis cambiaria:
74
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
• Déficit Público: Los modelos estudiados defienden que una economía que incrementa su gasto
público y decide financiar el déficit a través del incremento del crédito interno, provoca una
reducción compensatoria del nivel de reservas extranjeras del Banco Central, hasta llegar un
momento en que la oferta monetaria queda constituida exclusivamente por crédito interno. Esto
supone que la moneda del país quede sobrevalorada, lo que conduce a una depreciación
necesaria de la moneda. Por tanto, el incremento del déficit público, siempre que se financie a
través de crédito interno, puede ser un buen indicador de una futura crisis cambiaria.
• Indice de precios al consumo: Los modelos teóricos de primera generación parten de la
hipótesis del cumplimiento de la teoría del poder adquisitivo, es decir, que el tipo de cambio de
una moneda respecto a otra es igual al cociente de los índices de precios. Además, estos
modelos asumen que los precios extranjeros son constantes, por lo que las expectativas de
inflación se igualan a las expectativas de depreciación. De esta forma, las tenencias de moneda
nacional que los agentes desean mantener dependen de las expectativas de inflación, ya que
cuando se produce un incremento del nivel de precios, la moneda nacional se hace menos
atractiva, provocando que los residentes deseen deshacerse de sus tenencias de moneda
nacional a cambio de moneda extranjera, acudiendo para ello a las reservas del Banco Central.
Así, un incremento de los precios genera una disminución paulatina de las reservas del Banco
Central, dando lugar a un agotamiento de las mismas a través de un ataque especulativo que
provoca finalmente una devaluación de la moneda o un abandono del tipo de cambio fijo. Por
tanto el signo asociado a esta variable debe ser positivo.
• Diferencial de precios y Precios relativos: En el modelo realizado no sólo se ha analizado la
evolución del índice de precios, sino también el diferencial de precios respecto a Alemania, así
como los precios relativos entre el país correspondiente y Alemania. Estas variables han sido
incluidas con el objeto de medir las diferencias de competitividad, en el sentido de que una
pérdida de competitividad afecta al saldo de la balanza por cuenta corriente, y cuando se
producen sucesivos períodos de déficit por cuenta corriente es necesario devaluar la moneda
para financiar el déficit de la balanza. Dado que los agentes poseen expectativas perfectas, son
conscientes de que malos resultados de la balanza por cuenta corriente conducen a una
devaluación de la moneda, por lo que querrán cambiar la composición de su cartera a favor de
moneda extranjera, acudiendo por tanto a las reservas del Banco Central, y cuando éstas
alcancen su valor mínimo acabará produciéndose finalmente la crisis.
75
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
También se han medido los precios como variación de los precios relativos, en el sentido de
que cuanto mayores sean los incrementos de los precios de un país respecto a los precios de
Alemania, supondrá mayores pérdidas de competitividad que conducirán a una devaluación de
la moneda y a una probable crisis cambiaria. De esta forma, el signo asociado a estas dos
variables (diferencial de precios y precios relativos) debe ser positivo.
• Tipo de cambio efectivo real14 : Al igual que en el caso anterior, el tipo de cambio efectivo
real es un indicador que permite medir las pérdidas o ganancias de competitividad de una
economía a través de variaciones en los precios. La mayor parte de los modelos empíricos
señalan que las crisis financieras se encuentran precedidas por pérdidas de competitividad que
afectan a la Cuenta corriente y consecuentemente a la Balanza de Pagos, desembocando en un
crisis financiera. Dado que el tipo de cambio efectivo real es igual al tipo de cambio nominal de
una moneda respecto a otra de referencia, multiplicado a su vez por el cociente de los precios
relativos, un aumento del tipo de cambio efectivo real supone un incremento de los precios del
país, lo que supone pérdidas de competitividad y por tanto mayor probabilidad de crisis. Por
tanto el signo asociado a esta variable debe ser positivo.
• Crédito interno: Esta variable está muy relacionada con el nivel de reservas internacionales,
ya que la oferta monetaria está compuesta por la suma de ambas variables. Una política
monetaria expansiva no resulta compatible con el mantenimiento de un régimen de tipo de
cambio fijo, por lo que una expansión del crédito interno en una economía hace que los agentes
se formen expectativas sobre una futura devaluación de la moneda, provocando que deseen
cambiar la composición de su cartera en favor de moneda extranjera, generando un ataque
especulativo contra las reservas del Banco Central y provocando finalmente la devaluación de
la moneda (en el caso de un régimen de tipo de cambio deslizante), o el abandono del sistema
de tipo de cambio (en el caso de un régimen de tipo de cambio fijo). Por tanto, un aumento del
crédito interno es un indicador que refleja un aumento de la probabilidad de crisis financiera.
Otra forma de medir la evolución de esta variable es a través del ratio sobre la oferta monetaria,
ya que aumentos de la proporción del crédito interno sobre la M2 suponen disminuciones de la
proporción de las reservas sobre la oferta monetaria, y por tanto mayor probabilidad de crisis.
14
Aunque a priori resulte dudosa la inclusión de esta variable como variable explicativa al incluir en sí misma a la
variable endógena, en realidad no es así porque tal y como se explica más adelante, esta variable se incluye en el
modelos retardada como la media de los tres meses anteriores a que se produzca la primera depreciación fuerte de la
moneda. Por tanto, lo que se está midiendo es la tendencia de esta variable durante los períodos previos a una “crisis”.
76
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
De nuevo el signo asociado tanto a la variación del crédito interno como al ratio del crédito
interno sobre la oferta monetaria es positivo.
• Balanza por Cuenta Corriente: Una economía que registra déficits consecutivos por cuenta
corriente, hace que al gobierno del país le resulte imposible mantener el tipo de cambio,
provocando un abandono del régimen del tipo de cambio fijo o una devaluación de la moneda
(con el fin de incrementar las exportaciones y favorecer el saldo de la balanza). Los modelos
teóricos estudiados en el capítulo I.1., parten del supuesto de expectativas perfectas, por lo que
los agentes privados ante un déficit permanente de la cuenta corriente anticipan el abandono del
tipo de cambio, lo que les conduce a cambiar la composición de sus carteras a través de ventas
de sus tenencias de activos nacionales al Banco Central a cambio de activos en moneda
extranjera. Esta situación genera un ataque especulativo contra la moneda del país, haciendo
que las reservas del Banco Central disminuyan rápidamente hasta alcanzar su nivel mínimo,
momento en el cual el gobierno se ve obligado a abandonar el tipo de cambio. Por tanto el
signo asociado a esta variable debe ser negativo.
• Reservas Internacionales: Todos los autores coinciden en señalar que una pérdida gradual de
reservas del Banco Central da lugar a una crisis de balanza de pagos, provocando una crisis
cambiaria que supone un abandono del régimen de tipo de cambio fijo o una devaluación de la
moneda. Por tanto, la evolución de las reservas internacionales es un indicador de la posible
cercanía de una crisis cambiaria, en el sentido de que cuando se producen fuertes
disminuciones de las reservas de moneda extranjera del Banco Central, es muy probable que se
produzca una crisis cambiaria. Algunos autores incluyen la evolución de las reservas no como
variable explicativa, sino como variable necesaria y complementaria a la variación del tipo de
cambio para la definición de los períodos de crisis 15 . Por tanto, la relación de la evolución del
nivel de reservas con la probabilidad de una crisis es negativa, ya que fuertes caídas del nivel
de reservas suponen mayor probabilidad de crisis.
Al igual que se hizo con el crédito interno, es interesante analizar también la evolución del ratio
de las reservas internacionales sobre la M2, ya que cuanto mayor es el peso de las reservas
sobre la oferta monetaria, mayor capacidad posee el gobierno del país para defender el tipo de
cambio de su moneda, y por tanto existirán menores probabilidades de crisis cambiarias. En
este sentido la relación entre el ratio Reservas/ M2 y la probabilidad de crisis es negativa.
15
Ver Kaminsky y Reinhart (1996) “The Twin Crisis: The causes of Banking and Balance-of-Payments Problems”.
77
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Adicionalmente, se han analizado también las reservas del Banco Central pero medidas en
millones de dólares, siendo el signo en este caso también negativo.
•
Producto Interior Bruto: Aunque los modelos teóricos de primera generación no utilizan el
crecimiento del producto interior bruto como variable explicativa de una crisis financiera, no
se ha querido dejar sin analizar esta variable como explicativa, por considerar que los períodos
de crecimiento económico proporcionan estabilidad al país, y por tanto alejan las
probabilidades de crisis cambiaria, lo que supone que la relación entre el crecimiento del PIB y
la probabilidad de crisis es negativa. También se ha querido observar el comportamiento de
este indicador para la previsión del riesgo cambiario, ya que es común encontrar el PIB como
variable explicativa entre las aplicaciones prácticas existentes.
Una vez definidas todas las variables que iban a ser utilizadas en el modelo como
explicativas, el siguiente paso para la realización del modelo fue recopilar la información de cada
una de estas variables para cada uno de los nueve países analizados. En el siguiente cuadro se
recogen todas estas variables, así como las distintas unidades de medida en que han sido
analizadas con el objeto de conocer de qué forma aportan mayor capacidad explicativa al modelo:
Variable
Unidades de medida
Reservas Internacionales sin oro −
−
−
Crédito Interno
−
−
−
Indice de precios al consumo
−
−
−
−
−
Tipo de Cambio Efectivo Real
−
Balanza por Cuenta Corriente
−
Fuente
Tasas de variación intermensuales
Ratio mensual Reservas/ M2
Niveles (millones de USD)
Niveles (millones de USD)
Tasas de variación intermensuales
Ratio mensual Crédito Interno/ M2
Tasas interanuales
Tasas intermensuales
Diferencial de precios mensual
respecto al índice de precios alemán
(IP Alem.- IP País)
Precios mensuales relativos respecto
al índice de precios alemán (IP
Alem/ IP País)
Variación mensual de los precios
relativos
Tasas de variación intermensuales
−
Ratio BCC/PIB (%). Trimestral y
anual
−
−
−
−
−
−
−
−
−
78
Fondo Monetario Internacional
(International Financial Statistics)
The Economist
Fondo Monetario Internacional
(International Financial Statistics)
Fondo Monetario Internacional
(International Financial Statistics)
OCDE (Main Economic Indicators)
The Economist
Fondo Monetario Internacional
(International Financial Statistics)
Fondo Monetario Internacional
(International Financial Statistics)
OCDE (Main Economic Indicators)
The Economist
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Variable
Unidades de medida
Déficit Público
−
Ratio Déficit Público/ PIB (%).
Anual
Producto Interior Bruto
−
−
Niveles
% Crecimiento anual
Fuente
−
−
−
−
−
Fondo Monetario Internacional
(International Financial Statistics)
Banco Mundial
Fondo Monetario Internacional
(World Economic Outlook,
International Financial Statistcs)
OCDE (Main Economic Indicators)
The Economist
Partiendo de la base de datos inicial, se realizaron diferentes pruebas utilizando distintos
valores de las variables para los períodos de crisis. La principal diferencia entre las tres pruebas
realizadas, se refiere a los datos de las variables de frecuencia mensual, ya que en la primera de las
pruebas se ha utilizado como dato en los períodos de crisis el valor de la variable correspondiente
al mes anterior. En la segunda prueba, el dato utilizado ha sido la media de los tres meses
anteriores, y en la última prueba (Prueba 3), se han utilizado como datos para los períodos de
crisis, la media de los seis meses anteriores.
Respecto a las variables de periodicidad trimestral, los datos de las variables en los
períodos de crisis fueron el trimestre anterior para la Prueba 1 y 2, y la media de los dos trimestres
anteriores para el caso de la prueba 3.
Por último, las variables de frecuencia anual han sido incluidas en el modelo de igual
forma en las tres pruebas realizadas: se utiliza el dato correspondiente al año anterior cuando la
crisis se produce durante los primeros seis meses del año, y el dato del año cuando el período de
crisis se produce durante el segundo semestre del año.
En cuanto a los períodos de calma, en todas las pruebas se utilizaron los mismos datos,
correspondiéndose con la media de la variable a lo largo de cada período de calma. En el siguiente
cuadro se recogen las características de las distintas pruebas:
PRUEBA
PRUEBA 1
PRUEBA 2
PRUEBA 3
Periodicidad de los datos
Dato escogido en períodos de crisis
Variables Mensuales
Dato del mes anterior
Variables Trimestrales
Dato del trimestre anterior
Variables Mensuales
Media de los tres meses anteriores
Variables Trimestrales
Dato del trimestre anterior
Variables Mensuales
Media de los seis meses anteriores
Variables Trimestrales
Media de los dos trimestres anteriores
79
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Una vez construidas las tres bases de datos distintas, se realizó un análisis individual de
cada una de las variables en las distintas pruebas, con el fin de conocer qué tipo de datos resultaba
más significativo de cara a la predicción de una crisis cambiaria.
En el siguiente cuadro se muestra el resultado de las regresiones individuales para cada
una de las variables de periodicidad mensual16 en cada una de las bases de datos utilizadas, con su
nivel de significación y el ratio de verosimilitud correspondiente:
-0,393193
-1,518261
-1,536215
Nivel de
significación
0,6942
0,1289
0,1245
Ratio de
verosimilitud
0,003208
0,063033
0,067887
Prueba 1
Prueba 2
Prueba 3
-0,754076
-0,751449
-0,686600
0,4508
0,4524
0,4923
0,013149
0,013859
0,010640
Nivel de
reservas
Prueba 1
Prueba 2
Prueba 3
-1,048107
-1,836259
-1,112472
0,2946
0,0663
0,2659
0,024332
0,100192
0,028002
Variación del
crédito interno
Prueba 1
Prueba 2
Prueba 3
-0,236696
0,307689
-0,547626
0,8129
0,7583
0,5839
0,001136
0,002044
0,006190
Crédito interno
sobre M2
Prueba 1
Prueba 2
Prueba 3
1,304759
1,386700
1,082192
0,1920
0,1655
0,2792
0,034978
0,042206
0,023624
Variación anual
del IPC
Prueba 1
Prueba 2
Prueba 3
0,357427
0,539781
0,634310
0,7208
0,5893
0,5259
0,002660
0,006524
0,008564
Variación
mensual del IPC
Prueba 1
Prueba 2
Prueba 3
1,875195
2,034829
1,810812
0,0608
0,0419
0,0702
0,167078
0,216953
0,194088
Diferencial de
precios respecto
a Alemania
Prueba 1
Prueba 2
Prueba 3
-1,092969
-1,119337
-1,154323
0,2744
0,2630
0,2484
0,053984
0,059521
0,059412
Variables
Datos
Estadístico z
Variación de
reservas
Prueba 1
Prueba 2
Prueba 3
Reservas/ M2
16
Sólo se incluyen los resultados de las pruebas sobre las variables mensuales, porque es donde se diferencian las
variables, ya que los valores de las variables de frecuencia trimestral y anual son muy similares en las pruebas.
80
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
-1,118817
Nivel de
significación
0,2632
Ratio de
verosimilitud
0,055663
Prueba 2
Prueba 3
-1,148012
-1,187463
0,2510
0,2350
0,061523
0,061660
Variación de los
precios relativos
Prueba 1
1,837147
0,0662
0,161046
Prueba 2
Prueba 3
2,061665
1,799659
0,0392
0,0719
0,223401
0,197906
Variación del
tipo de cambio
efectivo real
Prueba 1
0,325748
0,7446
0,002155
Prueba 2
Prueba 3
0,230542
1,213845
0,8177
0,2248
0,001137
0,049801
Variables
Datos
Estadístico z
Precios relativos
respecto a
Alemania
Prueba 1
Atendiendo simultáneamente al nivel de significación de la variable y al ratio de
verosimilitud, se obtienen mejores resultados cuando se utilizan los datos correspondientes a la
media de los tres meses anteriores (Prueba 2), seguidos por los datos correspondientes a la media
de los seis meses anteriores (Prueba 3). En ninguno de los casos las variables resultan más
significativas cuando el dato utilizado es el del mes anterior (Prueba 1). Por este motivo se decidió
trabajar con la base de datos correspondiente a la Prueba 2.
II.5. ANÁLISIS INDIVIDUAL DE LAS VARIABLES
Las características de las variables objeto de estudio, por un lado una variable discreta
dicotómica (probabilidad de crisis), y por otro variables continuas, no permiten realizar un análisis
de correlaciones entre cada una de las explicativas y la variable endógena.
Por este motivo, el análisis individual de cada una de las variables ha consistido en la
realización de regresiones logísticas entre la variable endógena y cada una de las variables
explicativas, con el fin de conocer qué variables resultan más significativas de manera individual,
y si el signo obtenido se corresponde con el esperado.
Adicionalmente, con el objeto de completar el análisis y conocer las causas que provocan
la falta de significativad de determinadas variables, se ha realizado también un análisis de la
varianza (ANOVA17 ) entre la variable endógena y cada una de las variables explicativas.
17
El Análisis de la Varianza es una técnica de análisis entre variables cuyo objeto es conocer si los niveles de una
variable cualitativa influyen sobre los valores de una variable de tipo continuo. Para ello, esta herramienta se basa en la
comparación de las medias de la variable continua en cada uno de los grupos definidos por los niveles de la variable
81
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
En el caso de las estimaciones logísticas, el paquete estadístico utilizado ha sido E-Views,
mientras que para el caso de los análisis de la varianza, se ha utilizado como herramienta
informática el programa estadístico SPSS.
II.5.1. Variación mensual de reservas (V_RES)
La regresión resultante de estimar la probabilidad de crisis en función de la variación
mensual de reservas internacionales expresa que la relación causal entre ambas variables es
correcta en signo, ya que disminuciones del nivel de reservas implican aumentos de la
probabilidad de crisis. Sin embargo, esta variable no resulta estadísticamente significativa, ya que
el nivel de significación obtenido es 0,1289, debiendo ser 0,05 o inferior para poder aceptar su
validez estadística para un nivel de confianza del 95%. Del mismo modo, el ratio de verosimilitud
resulta demasiado bajo siendo 0,063.
En cuanto al porcentaje de aciertos tanto en los períodos de calma como en los de crisis, se
puede observar que a través de esta variable se obtienen muy buenos resultados a la hora de
predecir los períodos de calma (94,7%), mientras que en los períodos de crisis el modelo apenas
acierta un 40,% de los casos. Esto se debe a que la variable reservas muestra un comportamiento
más heterogéneo en el caso de los períodos de crisis frente a los períodos de calma. Esto genera un
mayor número de puntos atípicos durante los períodos de crisis dificultando su estimación, tal y
como se muestra más adelante en el análisis del gráfico de residuos y en el análisis de la varianza.
En el total de la muestra, el porcentaje de aciertos es del 70,6%.
Tabla 1.1
Variación mensual de las Reservas
Coeficiente
Signo
z-Statistic
-0,070050
Correcto
-1,518261
Ratio de verosimilitud
Nivel de
significación
0,1289
0,063033
% de aciertos en períodos de calma
94,74%
% de aciertos en períodos de crisis
40,00%
% de aciertos total
70,59%
discreta (habrá tantos grupo como niveles tenga la variable discreta). Si las diferencias entre las medias de los grupos son
lo suficientemente elevadas, se dice que existe una relación de dependencia entre la variable continua y los niveles de la
variable cualitativa. Sin embargo, una de las hipótesis de las que parte el Análisis de la Varianza, es que la dispersión
dentro de cada grupo sea pequeña, ya que si no es así el resultado del análisis podría ser de no significatividad, aún
existiendo diferencias importantes entre los grupos.
82
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El gráfico de residuos derivado de esta regresión muestra que existen varios puntos
atípicos, correspondiéndose en su totalidad con períodos de crisis, los cuales se enumeran a
continuación:
Gráfico de residuos
1.0
•
Eslovenia: Crisis Feb. 92
•
Rumania: Crisis May.92 – Ago. 92
•
Rumania: Crisis Ene. 97 - Feb.97
•
Ucrania: Crisis Ago. 99
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
5
10
15
20
25
30
35
En las siguientes tablas se exponen los resultados obtenidos del Análisis de la varianza
entre la variable “variación mensual de las reservas” como variable dependiente, y la probabilidad
de crisis como variable independiente.
Tabla 1.2
Media
Desviación típica
Calma
3,3
6,0
Coeficiente de
variación
1,8
Crisis
-2,2
12,5
-5,8
15
Total
0,9
9,7
10,8
34
Nº de casos
19
Tabla 1.3
Suma de cuadrados
Grados lib.
Media cuadrática
Inter-grupos
250,092
1
250,092
Intra-grupos
2860,869
32
89,402
Total
3110,961
33
F
Sig.
2,797 0,104
Como se puede observar, existen importantes diferencias entre la media de la variable en
los períodos de calma (en los que las reservas aumentan en torno al 3,3%), y la media de la
variable en los períodos de crisis (en los que las reservas disminuyen una media del -2,2%). Sin
embargo, los resultados del ANOVA no son significativos, al obtenerse un nivel de significación
de 0,104, debiendo ser 0,05 o inferior. Esto se debe a la gran dispersión encontrada en los grupos
83
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
analizados, y especialmente en los períodos de crisis, donde la desviación típica es de ±12,5 puntos
porcentuales. En el caso de los períodos de calma la dispersión es de ± 6,0.
II.5.2. Ratio Reservas/ M2 (RES_M2)
El signo derivado de la regresión logística individual entre el ratio de las reservas
internacionales sobre la oferta monetaria y la probabilidad de crisis es correcto, ya que cuanto
mayor es este ratio, mayor margen de maniobra posee un país para defender su tipo de cambio, y
por tanto menor será la probabilidad de crisis. Sin embargo, la variable no resulta significativa
individualmente, obteniéndose además un ratio de verosimilitud muy pequeño (0,014).
Respecto al porcentaje de aciertos, la variable predice perfectamente los períodos de calma
analizados, ya que se obtiene un 100% de aciertos, mientras que en el caso de las crisis ocurre
exactamente lo contrario: 0% de aciertos. En el total de la muestra el porcentaje de aciertos es del
55,9%.
Tabla 2.1
Ratio Reservas/ M2
Coeficiente
Signo
z-Statistic
-0,003412
Correcto
-0,751449
Nivel de
significación
0,4524
0,013859
Ratio de verosimilitud
% de aciertos en períodos de calma
100,0%
% de aciertos en períodos de crisis
0,0%
% de aciertos total
55,9%
Tal y como muestra el gráfico de residuos, tan sólo existe un punto atípico importante que
se corresponde con el período de crisis de Hungría de marzo en 1995.
Gráfico de residuos
0.8
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
5
10
15
20
84
25
30
35
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Los resultados derivados del análisis de la varianza, muestran grandes diferencias entre la
media de la variable en los períodos de crisis y calma, ya que en los períodos de calma, la media es
casi el doble que en los períodos de crisis, siendo el ratio de las reservas sobre la M2 en los
períodos de calma del 57,8%, mientras que en los períodos de crisis disminuye hasta el 34%.
Tabla 2.2
Media
Desviación típica
Calma
57,8
94,3
Coeficiente de
variación
1,6
Crisis
34,0
84,9
2,5
15
Total
47,3
89,7
1,9
34
Nº de casos
19
Sin embargo, el ANOVA no resulta significativo (0,45 de nivel de significación) debido de
nuevo a la gran dispersión encontrada dentro de cada uno de los grupos, que en el caso de los
períodos de calma es del ± 94,3% y en los períodos de crisis del ± 84,9%.
Tabla 2.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
4745,82
1
4745,82
0,58
0,45
Intra-grupos
261046,34
32
8157,70
Total
265792,15
33
II.5.3. Nivel de Reservas (N_RES)
El signo asociado a la variable nivel de reservas cuando se realiza una regresión logística
entre esta variable y la probabilidad de crisis es correcto al ser éste negativo, ya que cuanto mayor
es el nivel de reservas de un país, mayor es su capacidad para mantener el tipo de cambio pese a
que se produzcan disminuciones del nivel de reservas.
Tabla 3.1
Nivel de Reservas Internacionales
Coeficiente
Signo
z-Statistic
-0,000210
Correcto
-1,836259
Ratio de verosimilitud
Nivel de
significación
0,0663
0,100192
% de aciertos en períodos de calma
52,63%
% de aciertos en períodos de crisis
68,75%
% de aciertos total
60,00%
85
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Aunque el nivel de significación exigido para aceptar una variable como estadísticamente
significativa es igual o menor a 0,05, el nivel obtenido al estimar esta variable con la variable
endógena ha resultado del 0,0663, muy cercano a 0,05, y por tanto se puede aceptar esta variable
como válida (aunque con una probabilidad menor al 95%), para la estimación por sí sola de la
probabilidad de crisis.
La bondad del ajuste medida a través del ratio de verosimilitud es 0,10. Respecto a los
porcentajes de aciertos, destaca que se obtienen mejores resultados en los períodos de crisis
(68,75%) que en los períodos de calma (52,63%), ya que en la mayoría de los casos los resultados
derivados de la estimación resultan mejores en los períodos de crisis.
Gráfico de residuos
Puntos atípicos
1.2
0.8
•
Hungría: Crisis Mar. 95
•
Rusia: Crisis Sep.98 - Ene. 99
0.4
0.0
-0.4
-0.8
5
10
15
20
25
30
35
Los resultados derivados de la regresión logística no permitían aceptar la significativad de
la variable a un 0,05 de nivel de significación, sin embargo, tal y como se puede observar en la
siguiente tabla, existen grandes diferencias entre el nivel de reservas durante los períodos de calma
y crisis. En los períodos de calma la media del nivel de reservas resulta más del doble que en los
períodos de crisis, aunque en ambos casos la dispersión es muy elevada.
Tabla 3.2
Media
Desviación típica
Calma
5339,1
5102,3
Coeficiente de
variación
1.0
Crisis
2282,5
2921,6
1.3
16
Total
3941,8
4464,8
1.1
35
Nº de casos
19
Estas grandes diferencias entre las medias permite que el análisis de la varianza resulte
significativo, con un nivel de significación del 0,04, mostrando la capacidad explicativa de esta
variable de cara a la previsión del riesgo cambiario.
86
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Tabla 3.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
81148286,3
1
81148286,3
4,49
0,04
Intra-grupos
596634232,5
33
18079825,2
Total
677782518,9
34
II.5.4. Variación Mensual del Crédito Interno (V_CRED)
Cuando se analiza la variación mensual del crédito interno para predecir la probabilidad de
crisis cambiaria, se obtiene un signo positivo y por tanto correcto. Esto es así porque cuanto más
crezca mensualmente el crédito interno, mayor será la probabilidad de crisis.
Sin embargo, la variable no resulta estadísticamente significativa, al obtenerse un nivel de
significación del 0,7583, frente al 0,05 exigido.
Por otra parte, el valor del ratio de verosimilitud es muy cercano a cero (0,002), siendo 1
su valor más deseable. Pese a estos malos resultados, el modelo se ajusta perfectamente durante los
períodos de calma, acertando el 100% de los mismos. En cambio, el porcentaje de aciertos de los
períodos de crisis es muy pequeño (tan solo el 13,3%), invalidando por tanto la capacidad
explicatoria individual de esta variable para la muestra y período analizado.
Tabla 4.1
Variación del Crédito interno
Coeficiente
Signo
z-Statistic
0,022937
Correcto
0,307689
Ratio de verosimilitud
Nivel de
significación
0,7583
0,002044
% de aciertos en períodos de calma
100,0%
% de aciertos en períodos de crisis
13,3%
% de aciertos total
61,76%
A continuación se muestra el gráfico de residuos, así como los principales puntos atípicos:
87
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Gráfico de residuos
0.8
0.6
0.4
•
Rumania: Crisis May. 92 - Ago. 92
•
Rumania: Crisis Mar. 99
•
Rusia: Crisis Sep.98 - Ene. 99
0.2
0.0
-0.2
-0.4
-0.6
5
10
15
20
25
30
35
El análisis de la varianza realizado arroja los mismos resultados obtenidos anteriormente,
ya que el nivel de significación asociado al test F es de 0,77. En este caso, la falta de
significatividad de la variable no se deriva únicamente de la alta dispersión de la misma tanto en
los períodos de calma como en los de crisis, sino que además, la media de la variación del crédito
interno en los períodos de calma (1,5%) es muy similar a la media de la variable durante los
períodos de crisis (2,0%), si bien es cierto que en los períodos de crisis la dispersión es mucho
mayor (6,8%).
Tabla 4.2
Media
Desviación típica
Calma
1,5
2,2
Coeficiente de
variación
1,5
Crisis
2,0
6,8
3,4
15
Total
1,7
4,7
2,8
34
Nº de casos
19
Tabla 4.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
2,07
1
2,07
0,09
0,77
Intra-grupos
737,03
32
23,03
Total
739,10
33
II.5.5. Ratio Crédito Interno sobre Oferta Monetaria (CRED_M2)
La relación causal entre el ratio del crédito interno sobre la oferta monetaria y la
probabilidad de crisis es correcta, ya que el signo asociado a esta variable al realizar la regresión
logística individualmente ha sido positivo, y tal y como se ha explicado en el apartado
88
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
correspondiente a la definición de las variables explicativas, incrementos del crédito interno sobre
la oferta monetaria suponen mayor probabilidad de crisis.
No obstante, el nivel de significación obtenido (0,1655) ha sido muy elevado como para
poder aceptar la significatividad estadística de la variable.
La bondad del ajuste, medida a través del ratio de verosimilitud ha resultado por otra parte
de tan solo un 0,0422. Adicionalmente, el porcentaje de aciertos, tanto en los períodos de calma
(63,1%) como en los de crisis (37,5%), ha sido también muy escaso.
Tabla 5.1
Ratio Crédito interno sobre M2
Coeficiente
Signo
z-Statistic
0,018391
Correcto
1,386700
Nivel de
significación
0,1655
0,042206
Ratio de verosimilitud
% de aciertos en períodos de calma
63,16%
% de aciertos en períodos de crisis
37,50%
% de aciertos total
51,43%
Es importante destacar la gran variabilidad que registra esta variable a lo largo de los
distintos períodos muestrales, dando lugar a un gran número de puntos atípicos, los cuales se
corresponden en su mayoría con períodos de crisis. Además, destaca el hecho de que un gran
número de estos puntos se producen durante los períodos de crisis definidos en Rumania, lo que
demuestra que el comportamiento de dicha variable es significativamente distinto en este país
respecto al resto de países incluidos en la muestra. En concreto, la media de esta variable durante
los períodos de crisis en Rumania es de 102,9%, mientras que en la muestra total es de 126,4%
•
Eslovenia: Crisis Feb. 92
•
Polonia: Crisis Mar. 92
•
Rumania: Crisis May.92 - Ago. 92
•
Rumania: Crisis Mar. 93 - Mar. 94
Gráfico de residuos
0.8
0.6
0.4
0.2
•
Rumania: Crisis Nov. 95
•
Rumania: Crisis Ene. 97 - Feb. 97
•
Rumania: Crisis Mar. 99
•
Rusia: Calma Ago. 99 - Jun. 00
0.0
-0.2
-0.4
-0.6
-0.8
5
89
10
15
20
25
30
35
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
No se observan diferencias importantes entre la media de la variable durante los períodos
de calma y su valor durante los períodos de crisis, ya que durante los períodos de calma el ratio del
crédito interno sobre la oferta monetaria es del 113%, y durante los períodos de crisis del 126%.
Tabla 5.2
Media
Desviación típica
Calma
113,4
27,2
Coeficiente de
variación
0,2
Crisis
126,4
26,9
0,2
16,0
Total
119,3
27,4
0,2
35,0
Nº de casos
19,0
Debido a esta proximidad entre las medias de las variables durante los períodos de calma y
crisis, el nivel de significación asociado al test F al realizar el análisis de la varianza resulta
demasiado elevado, haciendo que la variable no resulte estadísticamente significativa (nivel de
significación = 0,17).
Tabla 5.3
Suma de cuadrados
Grados lib.
Media cuadrática
Inter-grupos
1466,006
1
1466,006
Intra-grupos
24118,361
33
730,859
Total
25584,367
34
F
Sig.
2,006 0,166
II.5.6. Variación anual del Índice de Precios (INFLACION)
El signo que debe derivarse al estimar la probabilidad de riesgo cambiario en función de la
tasa anual de inflación es positivo, ya que cuanto mayores sean los precios, se producirá una
pérdida de competitividad del país que afectará al saldo de la balanza por cuenta corriente,
derivando en una depreciación de la moneda. Por tanto, un incremento del nivel de precios implica
una mayor probabilidad de crisis cambiaria.
Sin embargo, el índice de precios medido como tasa interanual no resulta significativo, ya
que se obtiene un nivel de significación muy superior al 0,05.
90
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Por otra parte, la bondad del ajuste es mínima, siendo el ratio de verosimilitud 0,0065. En
cuanto al porcentaje de aciertos, se obtiene casi un 89% en los períodos de calma, mientras que en
los períodos de crisis sobrepasa ligeramente el 10%.
Tabla 6.1
Variación anual del IPC
Coeficiente
Signo
z-Statistic
0,003263
Correcto
0,539781
Nivel de
significación
0,5893
0,006524
Ratio de verosimilitud
% de aciertos en períodos de calma
88,89%
% de aciertos en períodos de crisis
13,33%
% de aciertos total
54,55%
El gráfico de residuos muestra la existencia de varios puntos atípicos, de los cuales
destacan los siguie ntes:
Gráfico de residuos
0.6
•
Bulgaria: Calma Sep.97- Jun.00
0.4
•
Rumania: Crisis Nov. 95
0.2
•
Rumania: Crisis Ene.97 - Feb. 97
0.0
•
Rusia: Crisis Sep.98 - Ene. 99
-0.2
•
Ucrania: Crisis Ene.93 - Dic. 93
-0.4
•
Ucrania: Crisis Jun.94 - Oct. 95
-0.6
5
10
15
20
25
30
Aunque la media de los precios es mayor durante los períodos de crisis (52,1%) que
durante los períodos de calma (40,9%), esta diferencia no es demasiado elevada. Además, la
dispersión encontrada es en ambos caso muy superior a la media, siendo el coeficiente de
variación de Pearson en los períodos de calma de 18, y 15 en los períodos de crisis.
Tabla 6.2
Media
Desviación típica
Calma
40,9
52,9
Coeficiente de
variación
18
Crisis
52,1
67,9
15
15
Total
46,0
59,4
33
33
91
Nº de casos
18
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
La falta de homogeneidad dentro de cada grupo, hace que los resultados del análisis de la
varianza no resulten significativos, obteniéndose un nivel de significación de 0,6.
Tabla 6.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
1018,80
1
1018,80
0,28
0,60
Intra-grupos
112078,57
31
3615,44
Total
113097,37
32
II.5.7. Variación mensual del índice de precios (V_IPC)
Al igual que en el caso anterior, la relación causal entre la variación de los precios (en este
caso calculada como tasas intermensuales) debe ser positiva, ya que incrementos en el nivel de
precios se asocian a mayores probabilidades de crisis debido a las causas señaladas anteriormente.
Por tanto, el signo obtenido al estimar la probabilidad de crisis en función de la variación mensual
del índice de precios es correcto.
Adicionalmente la variable resulta significativa al llevar asociado un nivel de significación
inferior a 0,05 (0,0419), lo que demuestra la capacidad explicatoria de la variable por sí sola como
indicador de crisis cambiaria.
Tabla 7.1
Variación mensual del IPC
Coeficiente
Signo
z-Statistic
0,453678
Correcto
2,034829
Ratio de verosimilitud
Nivel de
significación
0,0419
0,216953
% de aciertos en períodos de calma
83,33%
% de aciertos en períodos de crisis
52,94%
% de aciertos total
68,57%
La bondad del ajuste medida a través del ratio de verosimilitud es 0,21, valor que puede
ser considerado como aceptable al incluir en la estimación una única variable.
92
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El porcentaje de aciertos obtenidos en los períodos de calma ha sido del 83%, mientras que
en los períodos de crisis empeora, acertando únicamente algo más del 50% de los casos. Cuando se
considera la muestra total el porcentaje de aciertos es del 68,57%.
El gráfico de residuos muestra como el número de puntos atípicos detectados es elevado,
destacándose un total de ocho:
Gráfico de residuos
•
Bulgaria: Crisis May.96 - Feb.97
•
Hungría: Crisis Mar. 95
•
Polonia: Crisis Sep. 93
•
Rumania: Crisis Nov.95
•
Rumania: Crisis Mar. 99
•
Rusia: Crisis Sep.98 - Ene.99
•
Ucrania: Crisis Sep.98 - Oct.98
•
Ucrania: Crisis Ago. 99
1.2
0.8
0.4
0.0
-0.4
-0.8
5
10
15
20
25
30
35
A continuación se muestran los valores medios de la variable durante los períodos de crisis
y calma. Tal y como se puede observar, las diferencias entre las medias son muy importantes,
siendo en el caso de los períodos de calma del 1,8% y en los períodos de crisis del 6,3%. La
dispersión es especialmente elevada durante los períodos de crisis, aunque en este caso la falta de
homogeneidad dentro de los grupos no afecta a la significatividad del análisis de la varianza
debido a la cuantía de las diferencias entre las medias.
Tabla 7.2
Media
Desviación típica
Calma
1,8
1,2
Coeficiente de
variación
0,7
Crisis
6,3
6,6
1,0
17
Total
4,0
5,1
1,3
35
Nº de casos
18
Los resultados derivados del análisis de la varianza ratifican las conclusiones derivadas del
análisis de regresión logística, ya que el nivel de significación obtenido en el ANOVA y asociado
al test F es de 0,01, lo que nos permite validar estadísticamente la significatividad de esta variable
de manera individual para la predicción del riesgo cambiario.
93
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Tabla 7.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
179,01
1
179,01
8,25
0,01
Intra-grupos
715,97
33
21,70
Total
894,98
34
II.5. 8. Precios relativos respecto al IPC alemán (PRERELA)
También se han analizado los precios en términos de la paridad del poder adquisitivo,
utilizando como país de referencia Alemania por los motivos señalados en el apartado 2 de este
capítulo. El signo que debe ir asociado a esta variable es positivo, ya que incrementos de los
precios del país correspondiente respecto a Alemania suponen pérdidas de competitividad, y por
tanto mayor será la probabilidad de crisis. De este modo, el signo obtenido al estimar la
probabilidad de crisis en función de esta variable no es correcto al haber resultado negativo. La
variable tampoco ha resultado significativa, ya que el nivel de significación asociado al coeficiente
es de 0,25.
Tabla 8.1
IPC País/ IPC Alemania
Coeficiente
Signo
z-Statistic
-0,260070
Incorrecto
-1,148012
Ratio de verosimilitud
Nivel de
significación
0,2510
0,061523
% de aciertos en períodos de calma
33,33%
% de aciertos en períodos de crisis
70,59%
% de aciertos total
51,43%
La bondad del ajuste también ha sido escasa (el ratio de verosimilitud resultante es 0,061),
y al contrario que en el resto de las variables, el porcentaje de aciertos es más elevado en los
períodos de crisis que en los períodos de calma. Sin embargo este resultado puede ser la
consecuencia de una relación espuria, dado que la relación causal obtenida entre la probabilidad de
crisis y los precios relativos no ha sido correcta.
En el siguiente gráfico se muestran los puntos atípicos detectados, los cuales se
corresponden con períodos de crisis en Rumania y Rusia:
94
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Gráfico de residuos
0.8
•
Rumania: Crisis Mar.99
•
Ucrania: Crisis Ago. 99
0.6
0.4
0.2
0.0
-0.2
-0.4
-0.6
5
10
15
20
25
30
35
El signo obtenido en la estimación se puede justificar al observar los valores medios de la
variable durante los períodos de crisis y calma, ya que al contrario de lo que era de esperar, la
media de los precios relativos durante los períodos de calma es bastante superior a la media de los
mismos durante los períodos de crisis, dando lugar por tanto a un signo incorrecto en la
estimación.
Tabla 8.2
Media
Desviación típica
Calma
3,6
7,1
Coeficiente de
variación
2,0
Crisis
1,2
1,5
1,3
17
Total
2,4
5,3
2,2
35
Nº de casos
18
Por último, el análisis de la varianza realizado no resulta significativo, al ser el nivel de
significación asociado al test F superior a 0,05.
Tabla 8.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
50,5
1
50,5
1,85
0,18
Intra-grupos
901,5
33
27,3
Total
952,0
34
95
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.5. 9. Diferencial de precios respecto al IPC alemán (D_PRECIOS)
Otra forma de medir el efecto de los precios sobre la probabilidad de crisis, ha sido
calcular la diferencia del índice de precios respecto a Alemania. Para ello se ha generado una
variable consistente en la resta del índice de precios del país correspondiente menos el índice de
precios alemán. La interpretación económica de esta variable respecto a la probabilidad de crisis
cambiaria, es muy similar al razonamiento realizado para los índices de precios relativos. Cuando
el diferencial de precios es positivo, significa que los precios del país son superiores a los de
Alemania, y por tanto la probabilidad de crisis cambiaria será mayor debido a una pérdida de
competitividad del país correspondiente. El signo obtenido al estimar la probabilidad de crisis en
función del diferencial de precios es incorrecto, ya que debería haber sido positivo y sin embargo
ha resultado negativo.
Al igual que ocurría con los precios relativos, el diferencial de precios tampoco resulta
significativo, obteniéndose un nivel de significación de la variable de 0,2630.
Tabla 9.1
IPC País - IPC Alemania
Coeficiente
Signo
z-Statistic
-0,002417
Incorrecto
-1,119337
Ratio de verosimilitud
Nivel de
significación
0,2630
0,059521
% de aciertos en períodos de calma
27,78%
% de aciertos en períodos de crisis
70,59%
% de aciertos total
48,57%
El ratio de verosimilitud obtenido ha sido tan solo 0,059, y el porcentaje de aciertos sobre
el total no llega al 50%, lo que demuestra los malos resultados derivados de la estimación de la
probabilidad de crisis en función de esta variable. Es importante destacar que al igual que ocurría
con los precios relativos el porcentaje de aciertos en este caso es mayor en los períodos de crisis
que en los de calma.
En el gráfico se muestran los puntos atípicos detectados, que al ser la misma variable que
los precios relativos, aunque incorporada al modelo de una manera ligeramente diferente (una
como cociente y otra como diferencia), los puntos atípicos resultantes son los mismos:
96
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Gráfico de residuos
0.8
0.6
•
Rumania: Crisis Mar. 99
•
Ucrania: Crisis Ago. 99
0.4
0.2
0.0
-0.2
-0.4
-0.6
5
10
15
20
25
30
35
La media de la variable tanto en los períodos de crisis como en los de calma es positiva, lo
que significa que independientemente del período muestral, los precios de cada uno de los países
analizados son mayores que los de Alemania. Además, tal y como muestran estos datos, el
diferencial de precios es mayor en los períodos de calma que en los de crisis, cuando debería ser al
contrario. Esto explica el hecho de que el signo derivado de la estimación no sea correcto.
Tabla 9.2
Media
Desviación típica
Calma
270,0
745,7
Coeficiente de
variación
2,8
Crisis
21,5
157,4
7,3
17
Total
149,3
552,8
3,7
35
Nº de casos
18
El análisis de la varianza realizado sobre esta variable ratifica los resultados obtenidos a
través del análisis de regresión, ya que en este caso tampoco la variable resulta significativa (el
nivel de significación asociado al test F es de 0,19).
Tabla 9.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
539793,3
1
539793,3
1,81
0,19
Intra-grupos
9848961,6
33
298453,4
Total
10388755,0
34
97
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.5.10. Variación mensual de los precios relativos respecto al IPC alemán (V_PRERELA)
La importancia de los precios como variable fundamental causante de las crisis cambiarias,
ha llevado a que esta variable sea también medida como la variación de los precios relativos
respecto al índice de precios de Alemania. La interpretación económica en este caso, es que cuanto
mayor sea la variación de los precios relativos significará que cada período los precios de los
países analizados han crecido respecto a los precios de Alemania, por tanto mayor será la
probabilidad de crisis cambiaria.
En este caso, al igual que con la variación mensual de los precios, la variable sí resulta
significativa, ya que el nivel de significación obtenido al estimar la probabilidad de crisis en
función de la variación de los precios relativos es inferior a 0,05 (0,0392).
El ratio de verosimilitud obtenido ha sido 0,22, valor que puede considerarse bastante
aceptable al tratarse de una estimación que sólo incluye una variable explicativa.
Tabla 10.1
Variación de los precios relativos
Coeficiente
Signo
z-Statistic
0,487678
Correcto
2,061665
Ratio de verosimilitud
Nivel de
significación
0,0392
0,223401
% de aciertos en períodos de calma
83,33%
% de aciertos en períodos de crisis
52,94%
% de aciertos total
68,57%
Los resultados de la estimación en cuanto al porcentaje de aciertos son bastante buenos en
los períodos de calma (83,3%), sin embargo, el porcentaje de aciertos disminuye notablemente
durante los períodos de crisis, siendo en este caso de un 53%. Considerando la muestra total, el
porcentaje de aciertos es cercano al 70%.
Los puntos atípicos derivados de la estimación son los siguientes:
98
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Gráfico de residuos
•
Bulgaria: Crisis May.96- Feb.97
1.2
•
Hungría: Crisis Mar. 95
0.8
•
Polonia: Crisis Sep. 93
•
Rumania: Crisis Nov. 95
•
Rumania: Calma Sep.97 - Ago.98
•
Rusia: Crisis Sep.98 - Ene.99
•
Ucrania: Crisis Sep.98 - Oct.98
•
Ucrania: Crisis Ago. 99
0.4
0.0
-0.4
-0.8
5
10
15
20
25
30
35
El incremento medio de los precios durante los períodos de calma es sensiblemente menor
que el mismo durante los períodos de crisis, siendo del 1,5% durante los períodos de calma y del
6% durante los períodos de crisis. Se observa además, que la dispersión durante los períodos de
calma es inferior que en las crisis, sin embargo, esta falta de homogeneidad en los períodos de
crisis no impide que el análisis de la varianza resulte significativo, tal y como se muestra en la
Tabla 10.3., donde se obtiene un nivel de significación de 0,007.
Tabla 10.2
Media
Desviación típica
Calma
1,5
1,1
Coeficiente de
variación
0,7
Crisis
6,0
6,5
1,1
17
Total
3,7
5,0
1,4
35
Nº de casos
18
Tabla 10.3
Suma de cuadrados
Grados lib.
Media cuadrática
Inter-grupos
173,286
1
173,286
Intra-grupos
693,024
33
21,001
Total
866,309
34
99
F
Sig.
8,251 0,007
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.5.11. Variación mensual del tipo de cambio efectivo real (V_TCER)
Los modelos empíricos estudiados señalan el tipo de cambio efectivo real como uno de los
mejores indicadores de cara a la previsión de una crisis cambiaria. Sin embargo, tal y como se ha
incluido esta variable en el modelo, (como media de la variación mensual de los tres meses
anteriores a un período de crisis), y aplicada a la muestra y período definido, la variable no resulta
significativa al obtenerse un nivel de significación de 0,8177, pese a que el signo de la estimación
sí es correcto. Sin embargo, dado que lo se pretende medir a través de esta variable son las
pérdidas de competitividad del país y sí se han obtenido resultados satisfactorios con otras
variables que miden este mismo factor (variación de los precios relativos, variación de precios,
balanza por cuenta corriente), se ha considerado que el hecho de no poder incluir esta variable
posteriormente en el modelo por su falta de significatividad, no supondrá importantes pérdidas de
información.
Tabla 11.1
Variación del TC Efectivo Real
Coeficiente
Signo
z-Statistic
0,013948
Correcto
0,230542
Ratio de verosimilitud
Nivel de
significación
0,8177
0,001137
% de aciertos en períodos de calma
100,0%
% de aciertos en períodos de crisis
18,75%
% de aciertos total
61,76%
El ratio de verosimilitud obtenido ha sido también muy bajo (un 0,0011), y el porcentaje
de aciertos, aunque ha sido del 100% en los períodos de calma, en los períodos de crisis es tan solo
del 18%. En la muestra total el porcentaje de aciertos ha sido del 61,76%.
En el caso de esta variable no se detectan demasiados puntos atípicos, reduciéndose a dos
períodos de crisis definidas en Ucrania:
100
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Gráfico de residuos
0.8
0.6
0.4
•
Ucrania: Crisis Ene.93 - Dic.93
0.2
•
Ucrania: Crisis Jun.94 - Oct.95
0.0
-0.2
-0.4
-0.6
5
10
15
20
25
30
35
El análisis de la varianza tampoco resulta significativo, ya que además de que la diferencia
entre la media de la variación del tipo de cambio efectivo real durante los períodos de calma y
crisis es tan solo de 0,4 puntos porcentuales, la dispersión de esta variable tanto en los períodos de
calma como en los de crisis, y especialmente en estos últimos, es muy elevada.
Tabla 11.2
Media
Desviación típica
Calma
1,5
1,9
Coeficiente de
variación
1,3
Crisis
1,9
8,3
4,4
16
Total
1,7
5,8
3,4
34
Nº de casos
18
Tabla 11.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
1,74
1
1,74
0,05
0,82
Intra-grupos
1108,47
32
34,64
Total
1110,21
33
II.5.12. Balanza por Cuenta Corriente en porcentaje del PIB (BCCPIB)
La estimación de la probabilidad de crisis en función de la balanza por cuenta corriente
medida como porcentaje del PIB ha resultado significativa, ya que el nivel de significación
asociado al estadístico z ha sido de 0,02. Además, la relación causal entre las variables también ha
sido correcta, ya que el signo del coeficiente obtenido en la regresión ha resultado negativo, y tal y
como ya se ha indicado en apartados anteriores, saldos negativos de la balanza por cuenta corriente
101
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
implican mayor probabilidad de crisis, debido a que ante saldos negativos consecutivos de la BCC,
los gobiernos tenderán a depreciar la moneda con el fin de financiar el déficit y equilibrar la
balanza.
Tabla 12.1
BCC (% PIB)
Coeficiente
Signo
z-Statistic
-0,452600
Correcto
-2,252914
Nivel de
significación
0,0243
0,219674
Ratio de verosimilitud
% de aciertos en períodos de calma
88,89%
% de aciertos en períodos de crisis
54,55%
% de aciertos total
75,86%
El ratio de verosimilitud obtenido (0,21) arroja una bondad del ajuste muy aceptable para
tratarse de una estimación que sólo incluye una variable explicativa. El porcentaje de aciertos
muestra que esta variable tiene una gran capacidad explicativa durante los períodos de calma
(siendo en este caso el porcentaje de aciertos de casi el 90%), aunque en los períodos de crisis el
porcentaje de aciertos disminuye notablemente.
En el gráfico de residuos se muestran los puntos atípicos detectados, que en el caso de esta
variable resultan más pronunciados que en las variables analizadas anteriormente.
Gráfico de residuos
•
Bulgaria: Crisis May.96 - Feb.97
1.2
•
Polonia: Crisis Mar. 92
0.8
•
Rep. Eslovaca: Calma May.99 - Jun. 00
0.4
•
Rumania: Crisis May.92 - Ago.92
0.0
•
Rumania: Calma Sep.97 - Ago.98
-0.4
•
Rusia: Crisis Sep.98 - Ene.99
-0.8
5
10
15
20
25
30
La tabla 12.2 muestra los valores medios de la balanza por cuenta corriente en los períodos
de calma y crisis. Como puede observarse, el saldo de la cuenta corriente en estos países resulta
negativo en ambos períodos, aunque es menos deficitaria en los períodos de calma, siendo en este
caso el saldo del –2,0% del PIB, y del –5,6% del PIB en los períodos de crisis. Estas diferencias de
102
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
medias hacen que el análisis de la varianza resulte significativo, obteniéndose un valor del test F
de 6,84 con un nivel de significación asociado de 0,01.
Tabla 12.2
Media
Desviación típica
Calma
-2,0
3,9
Coeficiente de
variación
-2,0
Crisis
-5,6
3,1
-0,6
11
Total
-3,4
4,0
-1,2
29
Nº de casos
18
Tabla 12.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
89,39
1
89,39
6,84
0,01
Intra-grupos
352,93
27
13,07
Total
442,32
28
II.5.13. Déficit público en porcentaje del PIB (DEFICIT)
Según los modelos de primera generación la variable detonante de una crisis cambiaria es
una política fiscal expansiva financiada a través de crédito interno que produce una disminución
paulatina de las reservas del Banco Central, culminando finalmente en una crisis. Por tanto, el
signo asociado a esta variable debe ser positivo, en el sentido de que incrementos del déficit
público suponen mayor probabilidad de crisis cambiaria. Sin embargo, la regresión realizada en
función de esta variable da como resultado una relación inversa entre las variables, por lo que el
signo obtenido en la estimación es incorrecto.
Además, la variable tampoco ha resultado significativa, ya que el nivel de significación
obtenido ha sido de 0,11. El ratio de verosimilitud derivado de la estimación fue de 0,098, con un
porcentaje de aciertos en períodos de calma del 78,5% y del 33,3% en períodos de crisis.
Estos malos resultados, tanto de signo como de significatividad y bondad del ajuste, no
deben llevar a considerar esta variable como un mal indicador de la probabilidad de una crisis
cambiaria, ya que es precisamente en esta variable donde se han encontrado más dificultades a la
hora de la disponib ilidad de datos, lo que imposibilita interpretar correctamente los estadísticos
obtenidos por falta de grados de libertad. Por otra parte, también hay que tener en cuenta que esta
103
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
variable puede estar mal medida, ya que normalmente los gobiernos tardan alrededor de cuatro
años en publicar sus cifras definitivas sobre gasto público, haciendo que los datos incluidos en el
modelo puedan ser no homogéneos.
Tabla 13.1
Déficit Público (% PIB)
Coeficiente
Signo
z-Statistic
-0,250985
Incorrecto
-1,570339
Nivel de
significación
0,1163
0,098456
Ratio de verosimilitud
% de aciertos en períodos de calma
78,57%
% de aciertos en períodos de crisis
33,33%
% de aciertos total
60,87%
El gráfico de residuos muestra claramente esta carencia de datos señalada para un gran
número de los períodos muestrales analizados. Siendo conscientes de este defecto, se pueden
señalar aún así varios puntos que resultan especialmente atípicos, todos ellos detectados en
períodos de crisis definidos en Rumania.
Gráfico de residuos
1.2
0.8
•
Rumania: Crisis May.92 - Ago.92
•
Rumania: Crisis Nov. 95
•
Rumania: Crisis Ene.97 - Feb.97
•
Rumania: Crisis Mar. 99
0.4
0.0
-0.4
-0.8
5
10
15
20
25
30
La tabla 13.2 muestra que el déficit público es bastante más elevado en los períodos de
crisis (-4,9%), que en los períodos de calma (-2,5%). Sin embargo, la dispersión en ambos
períodos es alta, impidiendo por tanto que el análisis de la varianza resulte significativo (0,10 de
nivel de significación).
104
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Tabla 13.2
Media
Desviación típica
Calma
-2,5
2,8
Coeficiente de
variación
-1,1
Crisis
-4,9
3,8
-0,8
9
Total
-3,4
3,3
-1,0
23
Nº de casos
14
Tabla 13.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
30,61
1
30,61
2,99
0,10
Intra-grupos
214,69
21
10,22
Total
245,30
22
II.5.14. Crecimiento del Producto Interior Bruto (PIB)
Por último, se ha analizado el crecimiento del PIB real como variable explicativa de cara a
la predicción de una crisis cambiaria, ya que en principio, un país que registre un crecimiento
económico sostenido, es menos susceptible de sufrir una crisis cambiaria.
Cuando se estima la probabilidad de crisis en función de esta variable, el signo obtenido es
correcto y además la variable resulta significativa.
El ratio de verosimilitud resultante ha sido 0,1072, con un porcentaje de aciertos en los
períodos de calma de casi el 80%, y del 53% en los períodos de crisis.
Tabla 14.1
Crecimiento del PIB
Coeficiente
Signo
z-Statistic
-0,136801
Correcto
-2,060509
Ratio de verosimilitud
Nivel de
significación
0,0393
0,107263
% de aciertos en períodos de calma
78,95%
% de aciertos en períodos de crisis
52,94%
% de aciertos total
66,67%
Los principales puntos atípicos detectados son los siguientes, los cuales se producen
siempre en períodos de crisis:
105
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Gráfico de residuos
•
Bulgaria: Crisis May.96 - Feb.97
1.2
•
Hungría: Crisis Mar. 95
0.8
•
Polonia: Crisis Sep. 93
•
Rumania: Crisis Nov. 95
•
Rumania: Crisis Ene.97 - Feb.97
•
Ucrania: Crisis Sep.98 - Oct.98
•
Ucrania: Crisis Ago. 99
0.4
0.0
-0.4
-0.8
5
10
15
20
25
30
35
La tabla 14.2 muestra que existen grandes diferencias entre los crecimientos medios del
PIB durante los períodos de calma y crisis, siendo la media en el caso de los períodos de calma del
–0,1%, mientras que durante los períodos de crisis se producen decrecimientos mucho mayores,
con una media de –4,8%. Sin embargo, estas medias no resultan muy significativas para
caracterizar los períodos de crisis y calma según esta variable, ya que la dispersión encontrada en
ambos períodos es muy elevada, especialmente en el caso de los períodos de crisis.
Tabla 14.2
Media
Desviación típica
Calma
-0,1
3,7
Coeficiente de
variación
3,6
Crisis
-4,8
7,9
-1,6
17
Total
-2,3
6,4
-2,8
36
Nº de casos
19
Pese a la gran dispersión en ambos grupos, las diferencias entre la s medias permiten que el
análisis de la varianza resulte significativo para un nivel de significación del 0,03.
Tabla 14.3
Suma de cuadrados
Grados lib.
Media cuadrática
F
Sig.
Inter-grupos
199,69
1
199,69
5,46
0,03
Intra-grupos
1242,96
34
36,56
Total
1442,64
35
106
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.5.15. Resultados comparativos del análisis individual
En la siguiente tabla se muestran los resultados del análisis individual de las variables
explicativas obtenidos a través de las regresiones logísticas y del análisis de la varia nza. Las
variables aparecen ordenadas en la tabla en función del nivel de significación obtenido a través de
los ANOVAS realizados:
Resultados
ANOVA
Resultados regresiones LOGIT
Variables
z-Statistic
Variación de los precios
relativos
Variación mensual del
IPC
Nivel de
Ratio de
significación verosimilitud
% aciertos
períodos
calma
% aciertos
períodos
crisis
Significación
2,061665
0,0392
0,223401
83,33%
52,94%
0,007
2,034829
0,0419
0,216953
83,33%
52,94%
0,007
BCC (% PIB)
-2,252914
0,0243
0,219674
88,89%
54,55%
0,014
Crecimiento del PIB
Nivel de Reservas
Internacionales
Déficit Público (% PIB)
(*)
Variación mensual de
las Reservas
Ratio Crédito interno
sobre M2
IPC País/ IPC Alem. (*)
-2,060509
0,0393
0,107263
78,95%
52,94%
0,025
-1,836259
0,0663
0,100192
52,63%
68,75%
0,042
-1,570339
0,1163
0,098456
78,57%
33,33%
0,098
-1,518261
0,1289
0,063033
94,7%
40,0%
0,104
1,386700
0,1655
0,042206
63,16%
37,50%
0,166
-1,148012
0,2510
0,061523
33,33%
70,59%
0,183
IPC País – IPC Alem.
(*)
-1,119337
0,2630
0,059521
27,78%
70,59%
0,188
Ratio Reservas/ M2
-0,751449
0,4524
0,013859
100,0%
0,0%
0,451
88,89%
13,33%
0,599
100,0%
13,3%
0,766
100,0%
18,75%
0,824
Variación anual del IPC
0,539781
0,5893
0,006524
Variación del Crédito
0,307689
0,7583
0,002044
interno
Variación del TC
0,230542
0,8177
0,001137
Efectivo Real
(*) Los signos obtenidos en las regresiones logísticas fueron incorrectos
Atendiendo al nivel de significación derivado de los dos tipos de análisis, al signo
obtenido en las regresiones, al ratio de verosimilitud y a los porcentajes de aciertos, las variables
que mejores resultados arrojan de manera individual son las siguientes: Variación mensual del
IPC, Variación mensual de los precios relativos y la Balanza por Cuenta Corriente en porcentaje
del PIB. Otro segundo grupo de variables caracterizados por niveles de significación y porcentajes
de aciertos similares, pero ratios de verosimilitud inferiores, es el formado por las variables
crecimiento real del PIB y nivel de Reservas.
107
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
II.6. MODELO PARA LA DETERMINACIÓN DEL RIESGO CAMBIARIO EN LOS
PAÍSES DE EUROPA CENTRAL Y ORIENTAL
La realización del modelo para la estimación del riesgo cambiario en los países de Europa
Central y Oriental ha partido tanto de los resultados del análisis individual de variables, como de
las conclusiones extraídas a través de los modelos teóricos y empíricos analizados. Hay que
señalar que debido a las relaciones existentes entre las variables explicativas18 , los resultados del
análisis individual difieren de los obtenidos en el análisis conjunto, ya que una variable puede
resultar significativa de manera aislada, y en cambio no ofrecer buenos resultados en regresiones
multivariantes, debido a posibles problemas de multicolinealidad entre las variables. De hecho, de
las variables que mejores resultados han ofrecido en el análisis individual, tan sólo ha sido incluida
en el modelo final la variación mensual de los precios relativos. Incluso, podría decirse que se ha
incurrido en el caso de alguna variable, Balanza por Cuenta Corriente, en cierta traición teórica, ya
que la selección final de variables se ha basado finalmente en multitud de pruebas y análisis
empíricos. En nuestro descargo, sólo puede argumentarse que el modelo tiene un fin predictivo y
que a este objetivo se ha supeditado todo el proceso, eso sí, sin perder la orientación teórica de los
capítulos precedentes, tal y como puede deducirse de las variables seleccionadas.
En cuanto a la especificación concreta de cada variable y en comparación a la selección
individual realizada anteriormente, los comentarios siguientes son aclaratorios:
−
La variación mensual del IPC no fue incluida en el modelo ya que las estimaciones
multivariantes de la probabilidad de crisis ofrecían mejores resultados al incluir como variable
explicativa los precios relativos.
−
La Balanza por cuenta corriente había ofrecido muy buenos resultados al estimar la variable
endógena utilizando esta variable como único regresor, habiendo resultado significativa para
un nivel de confianza del 99% y obteniéndose un ratio de verosimilitud de 0,21. Sin embargo,
al realizar regresiones conjuntas introduciendo otras variables explicativas, ninguna de las
variables adicionales resultaba estadísticamente significativa, quedando siempre recogida toda
la capacidad explicativa del modelo a través de la variable de cuenta corriente. Por este
motivo, pese a que la mayoría de los trabajos señalan que déficits consecutivos en la balanza
18
Ver en Anexo I la matriz de correlaciones entre todas las variables explicativas.
108
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
por cuenta corriente muestran la proximidad de una crisis, el modelo que se presenta en este
trabajo no ha incluido finalmente esta variable.
−
El crecimiento del PIB no ha sido incluido en el modelo, porque aunque los resultados
individuales han sido buenos, al añadir nuevas variables explicativas al modelo, en la mayoría
de los casos la variable PIB no resultaba significativa.
−
El nivel de reservas no ha sido incluido en el modelo como variable explicativa, porque
aunque en el análisis individual los resultados derivados de esta variable eran mejores que los
derivados de la variació n de reservas, a la hora de realizar estimaciones conjuntas los
resultados mejoraban notablemente cuando la variable explicativa incluida era en tasas de
variación en lugar de niveles.
Por último, se ha considerado fundamental para la realización de un modelo de previsión
de riesgo cambiario la inclusión del crédito interno como variable explicativa, ya que todos los
autores defienden que la causa original de las crisis cambiarias es un aumento del crédito interno
para financiar el déficit público. Por este motivo, el modelo final ha incluido también como
variable explicativa el crédito interno medido como ratio sobre la oferta monetaria.
De esta forma, la especificación final del modelo para la predicción del riesgo cambiario
en los países de Europa Central y Oriental, ha quedado definida por las siguientes variables
explicativas:
•
Ratio del crédito interno sobre la oferta monetaria (CRED_M2)
•
Variación mensual de los precios relativos del país respecto al índice de precios
alemán (V_PRERELA)
•
Variación mensual del nivel de reservas (V_RES)
Según los modelos teóricos estudiados, estas variables son buenos indicadores de la
proximidad de una crisis cambiaria. Por un lado, todos los autores defienden que un aumento
sostenido del crédito interno conduce inevitablemente al debilitamiento de la moneda del país, y
por tanto a una devaluación de la misma o a un abandono del régimen del tipo de cambio fijo. Por
tanto, el ratio del crédito interno sobre la oferta monetaria, indica la evolución de la composición
de la oferta monetaria, en el sentido de que un aumento del peso del crédito interno sobre la M2,
109
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
supone una disminución del nivel de reservas internacionales, y es cuando éstas se agotan cuando
se produce finalmente la crisis cambiaria.
La variación de los precios relativos respecto al índice de precios alemán, indica las
ganancias o pérdidas de competitividad del país respecto a Alemania 19 . Cuando el nivel de precios
del país correspondiente aumenta respecto a los precios alemanes, se produce una pérdida de
competitividad, dando lugar a un aumento de las importaciones y a un descenso de las
exportaciones, empeorando el saldo de la balanza por cuenta corriente. Adicionalmente, los
modelos teóricos de primera generación asocian las expectativas de inflación a las expectativas de
depreciación, ya que asumen que el nivel de precios extranjeros es constante y que se cumple la
teoría de la paridad del poder adquisitivo. Estos modelos asumen también que los agentes poseen
expectativas perfectas, por lo que cuanto más aumenten los precios relativos, los agentes preverán
una depreciación de la moneda y querrán deshacerse de sus tenencias de moneda nacional a
cambio de moneda extranjera, generando de este modo un agotamiento de las reservas del Banco
Central que culminará en crisis cambiaria.
Por último, ya que es una disminución brusca e importante de las reservas la que provoca
finalmente la crisis, es imprescindible incluir en un modelo para la previsión del riesgo cambiario,
la evolución de las reservas durante los meses anteriores a que se produzca la misma.
Tal y como se comentó en el apartado anterior, los valores tomados para las variables en
los períodos de crisis, han sido la media de los tres meses anteriores al mismo, y durante los
períodos de calma, la media de la variable a lo largo de todo el período de calma.
La función logística estimada es la siguiente, mostrándose los resultados de la misma en la
tabla adjunta:
prob .crisis =
e ( − 6, 943144+ 0 ,042595CRED _ M 2+ 0, 846114V _ PRERELA − 0,186829V _ RES )
1 + e ( − 6,943144+ 0 ,042595CRED _ M 2+ 0,846114V _ PRERELA −0 ,186829V _ RES )
19
Se utiliza Alemania como país de referencia por ser éste el principal socio comercial del grupo de países analizados,
tal y como se ha señalado en el apartado 2 de este capítulo.
110
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Coeficiente
Signo
Nivel de
significación
-2,347759
0,0189
z-Statistic
C
-6,943144
-
Ratio Crédito interno/ M2
0,042595
Correcto
1,979879
0,0477
Variación precios relativos
0,846114
Correcto
2,291916
0,0219
Variación reservas internacionales
-0,186829
Correcto
-2,314896
0,0206
Suma cuadrática de errores
3,939497
% aciertos períodos calma20
94,44%
Logaritmo de verosimilitud
-13,22813
% aciertos períodos crisis
80,00%
Log. De verosimilitud modelo restr.
-22,73730
% aciertos períodos total
87,88%
Ratio de verosimilitud
0,418219 Observaciones totales
Observaciones Dep = 0
18
Observaciones Dep = 1
33
15
Todas las variables incluidas en el modelo han resultado estadísticamente significativas, ya
que en todos los casos el nivel de significación es igual o inferior a 0,05. Respecto al signo de las
variables, tambié n ha resultado el esperado.
Del mismo modo, el signo asociado a las variables es correcto, ya que cuanto mayor es la
proporción de crédito interno sobre la oferta monetaria, mayor es el aumento de los precios
relativos y mayor es la caída de las reservas, la probabilidad de crisis cambiaria aumenta.
El modelo incluye 33 de las 36 observaciones que componen la muestra, debido a la no
disponibilidad de datos para algunas variables. De estas 33 observaciones, 18 se corresponden con
períodos de calma y 15 con períodos de crisis, lo que hace que el modelo esté lo suficientemente
equilibrado y se eviten de esta manera sesgos que podrían distorsionar los resultados.
Con el fin de evitar problemas de multicolinealidad en el modelo, antes de continuar
analizando sus resultados, se ha comprobado que las correlaciones entre las variables explicativas
medidas a través del coeficiente de correlación de Pearson, no resulten importantes en ninguno de
los casos. Estas correlaciones se muestran en la siguiente tabla:
20
Se considera crisis si la probabilidad estimada es superior a 0,5
111
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Variación de
reservas
Ratio Crédito
interno/ M2
Variación
precios relativos
Variación de
reservas
Ratio Crédito
interno/ M2
Variación
precios relativos
1,000
0,065
0,128
0,065
1,000
-0,094
0,128
-0,094
1,000
Como puede observarse, la correlación máxima se produce entre la variación de los
precios relativos y la variación de las reservas, aunque aún así está correlación no llega tan siquiera
al 0,2. Se podría sospechar la existencia de problemas de multicolinealidad entre el crédito interno
sobre la oferta monetaria y la variación de las reservas, ya que la oferta monetaria está compuesta
por el crédito interno y las reservas. Sin embargo, dicha correlación no se produce porque al medir
ambas variables de forma diferente, lo que reflejan son aspectos distintos. De hecho la correlación
resultante entre ambas variables ha sido del 0,065.
La bondad del ajuste, medida a través del ratio de verosimilitud ha sido de 0,418, valor que
puede considerarse bastante aceptable al tratarse de un modelo logit. Los resultados del modelo
estimado son especialmente buenos cuando se analiza el porcentaje de aciertos tanto en los
períodos de calma como en los de crisis. Para ello se ha considerado que hay crisis cuando la
variable estimada toma valores iguales o superiores a 0,5, y se considera que hay calma cuando la
probabilidad de crisis estimada es inferior a 0,5.
Los mejores resultados del modelo se obtienen en los períodos de calma, donde el
porcentaje de aciertos es del 94,4%. También se obtienen buenos resultados en la predicción de los
períodos de crisis, aunque en este caso el porcentaje de aciertos es menor, siendo en este caso del
80%. Cuando se considera el total de la muestra, el porcentaje de aciertos es del 87,9%.
En el siguiente gráfico se muestra la evolución de la variable endógena y de la estimada,
así como el gráfico de los residuos. En él se pueden observar cuatro puntos atípicos especialmente
elevados:
112
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
1.0
0.8
0.6
0.4
0.2
0.0
1.0
0.5
0.0
-0.5
-1.0
5
10
15
Error
20
25
30
Real
35
Estimada
Los puntos atípicos detectados se corresponden con la crisis de septiembre de 1993 en
Polonia, el período de crisis de marzo de 1999 en Rumania, el período de calma de Rusia desde
enero de 1996 hasta febrero de 1998, y la crisis de agosto de 1999 en Ucrania.
Para analizar por qué estos períodos resultan atípicos, en la siguiente tabla se muestran los
valores de cada una de las variables en estos puntos de la muestra, comparándolos con la media de
las variables en los períodos de crisis o calma según corresponda:
Crédito interno/ M2
Polonia: Valor crisis Sep. 93
Rumania: Valor crisis Mar. 99
Rusia: Valor calma Ene.96-Feb. 98
Ucrania: Valor crisis Ago. 99
Media en período
de calma
111,7
144,6
Media en período
de crisis
123,7
111,7
91,3
-
151,2
Variación precios relativos
Polonia: Valor crisis Sep. 93
1,5
-
4,1
1,4
Rumania: Valor crisis Mar. 99
Rusia: Valor calma Ene.96-Feb. 98
1,1
2,6
Ucrania: Valor crisis Ago. 99
-
Variación de reservas
Polonia: Valor crisis Sep. 93
Rumania: Valor crisis Mar. 99
Rusia: Valor calma Ene.96-Feb. 98
Ucrania: Valor crisis Ago. 99
3,6
-0,3
-
113
0,3
-2,2
-0,2
1,2
17,0
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
El punto atípico originado por el período de crisis de septiembre 1993 en Polonia, se
caracteriza porque los valores obtenidos para cada una de las variables se alejan significativamente
de la media de las variables durante los períodos de crisis. Mientras que en la muestra total el ratio
del crédito interno sobre la oferta monetaria es del 123,7%, en septiembre de 1993 esta variable
toma el valor de 111,7%, valor coincidente con la media de la variable en los períodos de calma.
Respecto a la variación de los precios relativos, de nuevo se produce una situación semejante.
Mientras que en la muestra total el crecimiento medio de los precios relativos durante los períodos
de crisis es del 4,1%, en el caso de este punto muestral el crecimiento de los precios es del 1,4%,
muy cercano al crecimiento de los precios durante los períodos de calma (1,5%). Por último, las
reservas decrecen a una tasa media de –2,2% en los períodos de crisis para el total poblacional,
mientras que en el caso de la crisis definida por este punto atípico la reducción de las reservas es
tan solo el –0,2%.
El punto atípico definido por el período de crisis de marzo de 1999 en Rumania queda
reflejado claramente en el comportamiento del ratio del crédito interno sobre la oferta monetaria, y
de las reservas del Banco Central. En cuanto al crédito interno sobre la oferta monetaria, el valor
medio que toma esta variable en la muestra total durante los períodos de crisis es de 123,7%, sin
embargo en marzo de 1999 en Rumania la proporción del crédito interno sobre la M2 es mucho
menor, siendo del 91,3%. En el caso de las reservas, mientras que en la muestra total durante los
períodos de crisis decrecen a una tasa de -2,2%, en el caso de Rumania , en este dato muestral
crecen un 1,2%. Por último, también el crecimiento de los precios relativos es menor en este punto
que en el total muestral (2,6% frente al 4,1% del total).
El punto atípico asociado al período de calma de Rusia de Ene.96 - Feb.98, se debe por un
lado a que mientras en los períodos de calma la media del ratio del crédito interno sobre la oferta
monetaria es casi el 112%, en el caso de este dato muestral la proporción del crédito interno sobre
la M2 es de 144,6%, valor incluso muy superior a dicho ratio durante los períodos de crisis. La
otra causa que da lugar a que se produzca este punto “raro” es la variación de las reservas
internacionales, que en los períodos de calma suele mostrar incrementos mensuales en torno al
3,5%, mientras que en el caso de este período muestra una caída media del -0,3%.
Por último, el punto atípico detectado en agosto de 1999 en Ucrania, se debe
principalmente a la variación de las reservas internacionales, las cuales crecen en este punto un
17%, mientras que en la muestra total durante los períodos de crisis las reservas decrecen una
media del -2,2%. También se observan diferencias importantes en la variación de los precios
114
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
relativos, los cuales crecen en este punto un 0,3%, frente al crecimiento medio de los mismos
durante los períodos de crisis para el total de la muestra (4,1%). Por último, el ratio del crédito
interno sobre la M2 es sensiblemente mayor en este punto que la media de la variable en los
períodos de crisis, siendo un 151,2% frente al 123,7% del total poblacional.
Con el fin de caracterizar de algún modo tanto los períodos de crisis como los períodos de
calma, se muestran a continuación los valores medios, así como su dispersión, de las variables
explicativas incluidas en el modelo para cada uno de los períodos:
Períodos de calma
Períodos de crisis
Media
D.T.
Media
D.T.
Media
D.T.
Crédito interno/ M2
111,7
26,9
123,7
25,5
117,2
26,6
Variación precios relativos
1,5
1,1
4,1
3,8
2,7
3,0
Variación de reservas
3,6
6,0
-2,2
12,5
1,0
9,8
Nº observaciones
18
15
Muestra total
33
Según estos datos, los períodos de calma se caracterizan en media por ratios del crédito
interno sobre la oferta monetaria en torno al 111,7%, incrementos de los precios relativos respecto
a los precios alemanes del 1,5%, e incrementos mensuales del nivel de reservas del 3,6%. Sin
embargo, los períodos de crisis se caracterizan por un ratio del crédito interno superior en más de
diez puntos porcentuales a su valor durante los períodos de calma, incrementos de los precios
relativos superiores al 4%, y disminuciones de las reservas internacionales en torno al –2,2%.
No obstante la elevada dispersión de las variables hace que los valores medios no puedan
ser considerados como representativos, a excepción del ratio del crédito interno sobre la oferta
monetaria. Además, se observa que la dispersión de las variables es mayor en los períodos de crisis
que en los períodos de calma, destacando especialmente el caso de la variación de las reservas,
cuya desviación típica es más de seis veces el valor de la media durante los períodos de crisis, y
casi el doble de su media durante los períodos de calma.
115
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Aunque los resultados del modelo aquí presentado han sido bastante satisfactorios,
obteniéndose un porcentaje de aciertos a período histórico del 88% sobre el total de la muestra,
este trabajo es tan sólo una modesta aproximación a la elaboración de una herramienta para la
previsión de las crisis cambiaras, conscientes de las nuevas puertas abiertas en esta materia a
través de las nuevas teorías sobre crisis cambiarias derivadas de los modelos de segunda
generación.
El hecho de haber realizado un modelo típicamente de “primera generación” no supone el
querer poner un punto final a este trabajo, sino simplemente dar un primer paso fundamental hacia
este tipo de modelos, con el propósito de completar el trabajo inicialmente realizado a través de la
inclusión de las nuevas variables propuestas por los modelos más recientes, y a través de la
introducción de variables que permitan medir la interrelación entre las economías con el fin de
recoger de alguna forma los efectos de contagio tan comunes en nuestros días entre unos países y
otros cuando se produce una crisis cambiaria.
116
CAPITULO III:
CONCLUSIONES
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
III. CONCLUSIONES
Las principales conclusiones que se extraen de los trabajos teóricos analizados pueden
resumirse en los siguientes puntos:
•
Los modelos de primera generación concluyen que la causa de las crisis cambiarais se
encuentra en una inconsistencia entre las políticas fiscal y monetaria del gobierno con la
política cambiaria, reflejado en un aumento del gasto público financiado a través de crédito
interno que hace que resulte imposible el mantenimiento del tipo de cambio. Dado que estos
modelos parten de una hipotética situación en la que la oferta monetaria está únicamente
compuesta por reservas internacionales y crédito interno (M = R + C), un incremento del
crédito interno supone una disminución de las reservas de divisas del Banco Central para
mantener el equilibrio del mercado de dinero.
•
Asimismo, la mayoría de los modelos teóricos plantean que cuando las reservas comienzan a
disminuir, al poseer los agentes expectativas perfectas, éstos prevén el abandono del tipo de
cambio y deciden cambiar la composición de su cartera, vendiendo sus activos en moneda
nacional y comprando activos en moneda extranjera, acelerando de este modo el agotamiento
de las reservas. Este cambio en las tenencias deseadas de los agentes se debe a que cuando
éstos perciben que la moneda va a ser devaluada, cuanto mayor sea la cantidad de divisas
extranjeras que posean, podrán obtener mayores beneficios derivados de la diferencia entre los
tipos de cambio. Estas ganancias potenciales de capital generan un comportamiento
especulativo contra la moneda que acaba agotando las reservas del Banco Central,
produciéndose una crisis de balanza de pagos. Tras la crisis, la autoridad monetaria ya no
puede mantener el tipo de cambio puesto que las reservas han alcanzado su valor mínimo, y el
tipo de cambio a partir de ese momento o bien fluctúa libremente o la moneda es devaluada.
•
Otra alternativa planteada desde los modelos iniciales es que la crisis puede venir también
provocada por un cambio en las expectativas de inflación de los agentes. Los primeros
modelos parten del supuesto de que los precios extranjeros son constantes, por lo que las
expectativas de inflación se igualan a las expectativas de depreciación. En este caso, un
incremento de la inflación esperada supone que los agentes prevén una depreciación de la
moneda, por lo que deciden cambiar la composición de su cartera, adquiriendo activos en
118
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
moneda extranjera y vendiendo activos en moneda nacional, con la consiguiente disminución
de reservas que finaliza en una crisis de balanza de pagos.
Respecto a las principales conclusiones derivadas de los modelos empíricos se pueden
señalar las siguientes:
•
En general se mantiene que la política fiscal es más expansiva en los períodos anteriores a las
devaluaciones. En los casos en que se compara el comportamiento de un conjunto de variables
entre un grupo formado por países que han sufrido una devaluación y un grupo de control, se
observa que las diferencias entre los grupos son especialmente significativas en los indicadores
fiscales.
•
Los principales modelos aplicados observan que los períodos anteriores a las crisis se ven
caracterizados por una disminución de las reservas internacionales, medidos por el ratio de las
reservas sobre la M2, una apreciación del tipo de cambio efectivo real, un aumento del crédito
interno y del crédito al sector público, así como un aumento de la tasa de inflación interna.
También se han observado durante los períodos previos a las devaluaciones, déficits por
cuenta corriente, disminución de las exportaciones, crecimiento de la cantidad de dinero en
circulación, menores tasas de crecimiento del PIB y déficits fiscales.
Por último, atendiendo a los resultados derivados de la aplicación realizada para los países
de Europa Central y Oriental se pueden señalar los siguientes aspectos:
•
El análisis individual de las variables ha demostrado que, para el período y muestra analizado,
las variables con mayor capacidad predictiva son en primer lugar la Variación mensual del
IPC, la Variación mensual de los precios relativos, y la Balanza por Cuenta Corriente en
porcentaje del PIB. También han resultado buenos indicadores para la predicción de una crisis
cambiaria aunque con ratios de verosimilitud menores, el crecimiento del PIB y el nivel de
reservas internacionales. Atendiendo al porcentaje de aciertos, la variable que mejores
resultados ofrece es la Balanza por Cuenta Corriente, con un porcentaje de aciertos sobre el
total del la muestra del 75,9%, del 54,6% durante los períodos de crisis y del 88,9% en los
períodos de calma. En segundo lugar, la variación mensual de las reservas da lugar a un
porcentaje de aciertos sobre el total del 70,6%, mejorando los resultados respecto a la Balanza
por Cuenta Corriente durante los períodos de calma (94,7%), pero obteniendo un porcentaje de
aciertos algo inferior durante los períodos de crisis (40,0%).
119
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
•
A nivel agregado, con el fin de construir una herramienta para la predicción del riesgo
cambiario en los países de Europa Central y Oriental, el modelo finalmente especificado ha
incluido como variables explicativas el ratio del crédito interno sobre la oferta monetaria, la
variación mensual de los precios relativos, y la variación mensual de las reservas
internacionales. Los resultados del modelo a nivel global han sido bastante satisfactorios,
obteniéndose un porcentaje de aciertos sobre el total de la muestra del 87,9%, siendo muy
favorables durante los períodos de calma, en los que el porcentaje de aciertos ha sido del
94,4%, y algo peores en los períodos de crisis (80,0%). El ratio de verosimilitud derivado de la
estimación logit fue del 0,42.
•
Según los resultados obtenidos de la estimación del modelo, los períodos de calma se
caracterizan por ratios del crédito interno sobre la oferta monetaria en torno al 111,7%,
incrementos de los precios relativos respecto a los precios alemanes del 1,5%, e incrementos
mensuales del nivel de reservas del 3,6%. Los períodos de crisis en cambio, registran ratios
medios del crédito interno sobre la M2 cercanos al 124%, incrementos de los precios relativos
superiores al 4%, y disminuciones de las reservas internacionales por encima del –2%. Sin
embargo, estos resultados son tan sólo orientativos, ya que no pueden ser considerados
estadísticamente significativos al existir una dispersión muy elevada tanto en los períodos de
crisis como en los períodos de calma.
120
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Por último, no quisiera cerrar este trabajo sin incluir las líneas de investigación que el
autor pretende realizar en un futuro, que darán lugar a diferentes proyectos, artículos, y probable y
deseablemente a una tesis doctoral. Entre las diferentes alternativas, quisiera destacar las
siguientes:
−
Desarrollar un modelo compacto que incluya tanto las variables estudiadas en este trabajo,
como variables más acordes con los modelos de segunda generación, haciendo especial
hincapié en los efectos de contagio entre unas economías y otras.
−
Especificar la variable endógena no sólo a partir de las variaciones del tipo de cambio, sino
incluyendo también otras variables como la variación de las reservas del Banco Central y los
tipos de interés, tal y como han realizado otros autores.
−
Probar especificaciones diferentes al modelo logit que permitan utilizar todo el rango temporal
de las variables (tanto endógena como explicativas).
−
Enfrentar los resultados derivados de los modelos logit y probit con los derivados de los
indicadores de alerta, con el fin de conocer cuál de estos dos procedimientos resulta más
adecuado para la previsión de una crisis cambiaria.
121
BIBLIOGRAFÍA
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
-
Agénor P.R. y Flood R.P. (1994). “Macroeconomic Policy, Speculatuve Attacks, and Balance
of Payments Crisis”. En “The Handbook of International Macroeconomics”. Editado por
Frederick Van Der Ploeg (Cambrigde, Massachusetts; Oxford, Inglaterra: Blackwell), pp. 224250.
-
Bae r, Mónica (1994). “Un nuevo orden monetario-financiero internacional: las lecciones de
Bretton Woods”. “Economistas”. Editado por el Colegio de Economistas de Madrid. Nº61,
Año XII, pp.38-42.
-
Bajo, Oscar y Simón Sosvilla (1993). “Teorías del tipo de cambio: una panorámica”. Revista
de Economía Aplicada. Volumen I, Otoño 1993, pp. 175-205.
-
Blanco, Herminio y Peter M. Garber (1986). “Recurrent Devaluation and Specultative
Attacks on the Mexican Peso”. Jornal of Political Economy, 1986, vol. 94, nº 1, pp. 148-166.
-
Connolly, Michael B. y Dean Taylor (1984). “The Exact Timing of the Collapse of an
Exchange Rate Regime and Its Impact on the Relative Price of Traded Goods”. Journal of
Money, Credit and Banking. Vol. 16. Nº 2. (Mayo 1984), pp. 194-207.
-
Durán, Juan José (1997). “Mercado de Divisas y riesgo de cambio”. Ed. Piramide.
-
Edwards, Sebastian y Peter J. Montiel (1989). “Devaluation Crisis and the Macroeconomic
Consequences of Postponed Adjustment in Developing Countries”. IMF Staff Papers. Vol.
36. Nº 4 (Diciembre 1989). Pp. 875 – 903.
-
Edwars, Sebastian (1989). “Exchange Controls, Devaluations, and Real Exchange Rates: The
Latin American Experience”. Economic Development and Cultural Change. 1989.
-
Fernández Valbuena, Santiago (2000). “Las crisis cambia rias de finales del siglo XX:
hechos, teorías y políticas”. Lecturas de Economía Aplicada: Referencias a algunas
transformaciones derivadas de la Nueva Economía. Editado por IT&FI (International
Technical & Financial Institute), pp. 179 – 198.
123
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
-
Flood, Robert P. Y Peter M. Garber (1984). “Collapsing exchange – rate regimes: Some
linear examples”. Journal of International Economics. Vol. 17. Nº 1/2. (Agosto 1984), pp. 113.
-
Flood, Robert P. y Marion, Nancy P. (1997). “Policy Implications of Second-Generation
Crisis Model”. IMF Staff Papers. Vol. 44. Nº 3 (Septiembre 1997). Pp. 383 – 390.
-
Frankel Jeffrey A. Y Andrew K. Rose (1996). “Currency Crashes in Emerging Markets:
Empirical Indicators”. NBER, documento de trabajo nº 5437 (Cambridge, Massachussetts:
National Bureau of Economic Research). Enero 1996.
-
García Fernandez-Muro, Clara e Iliana Olivié Aldasoro (1999). “Modelos teóricos de
crisis de tipo de cambio y su aplicación a la crisis de Asia Oriental”. Facultad de CC.
Económicas y Empresariales, Universidad Complutense de Madrid, Documento de trabajo
9910.
-
García Santos, Mª Nieves (2000). “Los principios de la arquitectura financiera como base
para la política económica”. En “Lecturas de Economía Aplicada: Referencias a algunas
transformaciones derivadas de la Nueva Economía.” Editado por IT&FI (International
Technical & Financial Institute), pp. 133 – 177.
-
Gil Pérez-Andujar, A., Gregorio Izquierdo Llanes, Mercerdes Frielingsdorf y José Mª.
Goizueta Besga (1998). “La crisis Inédita”. Revista del Instituto de Estudios Económicos,
Nº4, 1998.
-
Herrarte Sánchez, Ainhoa, Eva Medina Moral y José Vicéns Otero (2000). “Modelos de
crisis financieras”. Instituto de Predicción Económica L.R. Klein, Facultad de CC.
Empresariales y Económicas, Universidad Autónoma de Madrid, Documento 00/01 (Enero
2000).
-
Hubbard, R. Glenn (1991). “Financial Markets and Financial Crisis”. Chicago: University of
Chicago Press, 1991. Project Report NBER.
124
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
-
Jovell, Albert J. (1995). “Análisis de Regresión Logística”. Centro de Investigacines
sociológicas (CIS). Cuardernos Metodológicos, nº 15, Madrid.
-
J.P. Morgan (1998). “Event Risk Indicator Handbook”. J.P. Morgan Exchange Research Ltd.
London. (Mayo 1998).
-
Kaminsky, Graciela, Saul Lizondo y Carmen M. Reinhart (1998). “Leading indicators of
Currency Crisis”. IMF Staff Papers. Vol. 45. Nº 1 (Marzo 1998), pp. 1 – 48.
-
Kaminsky, Graciela y Carmen M. Reinhart (1996). “The Twin Crisis: The Causes of
Banking and Balance of Payments Problems”. International Finance Discussion (Washington:
Board of Governors of the Federal Reserve System). Mayo 1996.
-
Krugman, Paul R. y Maurice Obstfeld (1995). “Economia Internacional”. Editorial Mc
Graw Hill.
-
Krugman, Paul R. (1979). “A model of Balance of Payments Crisis”. Journal of Money
Credit and Banking. Vol. 11, Nº 3 (Agosto 1979). Pp. 311 – 325.
-
Krugman, Paul R. (1992). “Currencies and crisis”. The MIT Press. Cambridge,
Massachusetts. London, England.
-
Kindleberger, Charles P. (1998). “El orden económico internacional”. Editorial Crítica.
-
Kindleberger, Charles P. (1991). “Manías, pánicos y cracs. Historia de las crisis financieras”.
Editorial Ariel Sociedad Económica. Octubre 1991.
-
Medina Moral, Eva (2000). “Modelos de segunda generación para la determinación del tipo
de cambio. Una aplicación a los países Latinoamericanos”. Trabajo de Tesina, Facultad de CC.
Económicas y Empresariales, Universidad Autónoma de Madrid.
-
Nenovsky, Nikolay, Kalin Hristov y Boris Petrov (1999). “Two Approaches to the Fixed
Exchange Rate Crises”. Bulgarian National Bank, Discussion Papers DP/4/1999. (Abril 1999).
125
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
-
Obstfeld, Maurice (1984). “Balance of Payments Crisis and Devaluation”. Journal of Money,
Credit and Banking. Vol. 16. Nº 2 (Mayo 1984). Pp. 208 – 217.
-
Obstfeld, Maurice (1996). “Models of Currency Crisis with Self-fulfilling features”.
European Economic Review, 40, pp. 1037-1047.
-
Rodríguez Prada, Gonzalo (1995). “La economía de los Currency Boards: Pasado y
presente”. En “Economistas”. Editado por el Colegio de Economistas de Madrid. Nº 63, Año
XIII, pp.114-121.
-
Ruiz Maya, Luis, F.Javier Martín Pliego, José Mª. Montero y Pilar Uriz Tomé (1995).
“Análisis estadístico de encuestas: Datos Cualtitativos”. Editorial AC, pp. 539-699.
-
Salant, Stephen W., y Dale W. Henderson. “Market Anticipation of Government Policy and
the Price of Gold”. Journal of Political Economy, 86 (Agosto 1978), pp. 627 – 648.
-
Velasco, Andrés (1987). “Financial Crisis and Balance of Payments Crisis. A simple Model
of the Southern Cone Experience”. Journal of Development Economics nº 27, pp. 263-283.
-
Vicéns Otero, José (1995). “Modelos con variables cualtitativas dicotómicas”. Instituto de
Predicción Económica L.R. Klein, Documento 95/5, (Noviembre 1995).
126
ANEXOS
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
DEFINICIÓN DE LAS VARIABLES EXPLICATIVAS
•
V_RES:
Variación mensual de las reservas internacionales
•
RES_M2:
% de Reservas internacionales sobre la oferta monetaria
•
N_RES:
Nivel de reservas (millones USD)
•
V_CRED:
Variación mensual del crédito interno
•
CRED_M2:
% Crédito interno sobre la oferta monetaria
•
INFLACION:
Variación anual del IPC
•
V_IPC:
Variación mensual del IPC
•
PRERELA:
Precios relativos respecto al IPC alemán
•
D_PRECIOS:
Diferencial de precios respecto al IPC alemán
•
V_PRERELA:
Variación mensual de los precios relativos respecto al IPC alemán
•
V_TCER:
Variación mensual del tipo de cambio efectivo real
•
BCCPIB:
Balanza por Cuenta Corriente (% PIB)
•
DEFICIT:
Déficit Público (% PIB)
•
PIB:
Cto. Anual del PIB
128
ANEXO I: MATRIZ DE CORRELACIONES
BCCPIB CRED_M2 D_PRECIOS DEFICIT INFLACION N_RES
PIB
PRERELA RES_M2 V_CRED V_IPC V_PRERELA V_RES V_TCER
BCCPIB
1,000
-0,029
0,155
0,469
-0,189
0,292
0,257
0,155
-0,267
-0,122
-0,413
-0,417
0,176
-0,344
CRED_M2
-0,029
1,000
-0,420
-0,711
-0,225
0,131
-0,110
-0,421
0,223
0,031
0,044
0,011
0,102
-0,398
D_PRECIOS
0,155
-0,420
1,000
0,434
0,423
-0,102
-0,031
1,000
-0,018
-0,119
-0,220
-0,205
-0,023
-0,066
DEFICIT
0,469
-0,711
0,434
1,000
0,316
-0,001
-0,048
0,433
-0,283
-0,338
-0,069
-0,042
0,365
0,211
INFLACION
-0,189
-0,225
0,423
0,316
1,000
-0,509
-0,618
0,420
-0,188
-0,239
0,663
0,667
0,294
0,486
N_RES
0,292
0,131
-0,102
-0,001
-0,509
1,000
0,265
-0,100
0,170
-0,044
-0,469
-0,489
-0,015
-0,409
PIB
0,257
-0,110
-0,031
-0,048
-0,618
0,265
1,000
-0,027
0,184
0,286
-0,612
-0,597
-0,362
-0,417
PRERELA
0,155
-0,421
1,000
0,433
0,420
-0,100
-0,027
1,000
-0,018
-0,118
-0,224
-0,208
-0,026
-0,068
RES_M2
-0,267
0,223
-0,018
-0,283
-0,188
0,170
0,184
-0,018
1,000
0,028
-0,203
-0,212
-0,078
-0,217
V_CRED
-0,122
0,031
-0,119
-0,338
-0,239
-0,044
0,286
-0,118
0,028
1,000
0,006
-0,007
-0,010
0,211
V_IPC
-0,413
0,044
-0,220
-0,069
0,663
-0,469
-0,612
-0,224
-0,203
0,006
1,000
0,997
0,265
0,772
V_PRERELA
-0,417
0,011
-0,205
-0,042
0,667
-0,489
-0,597
-0,208
-0,212
-0,007
0,997
1,000
0,279
0,790
V_RES
0,176
0,102
-0,023
0,365
0,294
-0,015
-0,362
-0,026
-0,078
-0,010
0,265
0,279
1,000
0,322
V_TCER
-0,344
-0,398
-0,066
0,211
0,486
-0,409
-0,417
-0,068
-0,217
0,211
0,772
0,790
0,322
1,000
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
ANEXO II: SALIDAS EVIEWS: REGRESIONES LOGÍSTICAS INDIVIDUALES
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 34
Excluded observations: 2
Convergence achieved after 2 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
V_RES
-0.182908
-0.070050
0.362183
0.046138
-0.505016
-1.518261
0.6135
0.1289
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.441176
0.488731
7.643469
-21.86054
-23.33116
2.941245
0.086344
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
19
15
0.503995
1.403561
1.493347
1.434181
-0.642957
0.063033
Total obs
34
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 34
Excluded observations: 2
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent Gain**
18
1
19
18
94.74
5.26
-5.26
NA
9
6
15
6
40.00
60.00
40.00
40.00
27
7
34
24
70.59
29.41
14.71
33.33
Estimated Equation
Dep=0 Dep=1
Total
E(# of Dep=0)
E(# of Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent Gain**
11.33
7.67
19.00
11.33
59.62
40.38
3.74
8.47
7.67
7.33
15.00
7.33
48.85
51.15
4.73
8.47
19.00
15.00
34.00
18.66
54.87
45.13
4.18
8.47
Constant Probability
Dep=0 Dep=1
Total
19
0
19
19
100.00
0.00
15
0
15
0
0.00
100.00
34
0
34
19
55.88
44.12
Constant Probability
Dep=0 Dep=1
Total
10.62
8.38
19.00
10.62
55.88
44.12
8.38
6.62
15.00
6.62
44.12
55.88
19.00
15.00
34.00
17.24
50.69
49.31
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
130
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 34
Excluded observations: 2
Convergence achieved after 3 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
RES_M2
-0.085391
-0.003412
0.393069
0.004540
-0.217241
-0.751449
0.8280
0.4524
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.441176
0.506474
8.208507
-23.00781
-23.33116
0.646701
0.421295
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
19
15
0.503995
1.471048
1.560834
1.501667
-0.676700
0.013859
Total obs
34
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 34
Excluded observations: 2
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
19
15
34
19
15
34
0
19
19
100.00
0.00
0.00
NA
0
15
0
0.00
100.00
0.00
0.00
0
34
19
55.88
44.12
0.00
0.00
0
19
19
100.00
0.00
0
15
0
0.00
100.00
0
34
19
55.88
44.12
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
10.78
8.22
19.00
10.62
8.38
19.00
8.22
6.78
15.00
8.38
6.62
15.00
19.00
10.78
56.73
43.27
0.85
1.93
15.00
6.78
45.20
54.80
1.08
1.93
34.00
17.56
51.64
48.36
0.95
1.93
19.00
10.62
55.88
44.12
15.00
6.62
44.12
55.88
34.00
17.24
50.69
49.31
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
131
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 35
Excluded observations: 1
Convergence achieved after 6 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
N_RES
0.557297
-0.000210
0.492141
0.000114
1.132394
-1.836259
0.2575
0.0663
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.457143
0.479640
7.591813
-21.71364
-24.13142
4.835568
0.027878
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
19
16
0.505433
1.355065
1.443942
1.385745
-0.620390
0.100192
Total obs
35
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 35
Excluded observations: 1
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
10
5
15
19
16
35
9
19
10
52.63
47.37
-47.37
NA
11
16
11
68.75
31.25
68.75
68.75
20
35
21
60.00
40.00
5.71
12.50
0
19
19
100.00
0.00
0
16
0
0.00
100.00
0
35
19
54.29
45.71
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
11.40
7.60
19.00
10.31
8.69
19.00
7.60
8.40
16.00
8.69
7.31
16.00
19.00
11.40
59.99
40.01
5.71
12.48
16.00
8.40
52.49
47.51
6.78
12.48
35.00
19.80
56.56
43.44
6.20
12.48
19.00
10.31
54.29
45.71
16.00
7.31
45.71
54.29
35.00
17.63
50.37
49.63
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
132
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 34
Excluded observations: 2
Convergence achieved after 3 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
V_CRED
-0.276812
0.022937
0.370650
0.074547
-0.746828
0.307689
0.4552
0.7583
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.441176
0.510946
8.354101
-23.28349
-23.33116
0.095355
0.757477
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
19
15
0.503995
1.487264
1.577050
1.517884
-0.684808
0.002044
Total obs
34
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 34
Excluded observations: 2
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
19
13
32
19
15
34
0
19
19
100.00
0.00
0.00
NA
2
15
2
13.33
86.67
13.33
13.33
2
34
21
61.76
38.24
5.88
13.33
0
19
19
100.00
0.00
0
15
0
0.00
100.00
0
34
19
55.88
44.12
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
10.64
8.36
19.00
10.62
8.38
19.00
8.36
6.64
15.00
8.38
6.62
15.00
19.00
10.64
56.02
43.98
0.14
0.31
15.00
6.64
44.29
55.71
0.17
0.31
34.00
17.29
50.84
49.16
0.15
0.31
19.00
10.62
55.88
44.12
15.00
6.62
44.12
55.88
34.00
17.24
50.69
49.31
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
133
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 35
Excluded observations: 1
Convergence achieved after 4 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
CRED_M2
-2.373146
0.018391
1.627289
0.013262
-1.458343
1.386700
0.1447
0.1655
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.457143
0.499062
8.219086
-23.11292
-24.13142
2.036999
0.153512
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
19
16
0.505433
1.435024
1.523901
1.465704
-0.660369
0.042206
Total obs
35
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 35
Excluded observations: 1
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
12
10
22
19
16
35
7
19
12
63.16
36.84
-36.84
NA
6
16
6
37.50
62.50
37.50
37.50
13
35
18
51.43
48.57
-2.86
-6.25
0
19
19
100.00
0.00
0
16
0
0.00
100.00
0
35
19
54.29
45.71
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
10.80
8.20
19.00
10.31
8.69
19.00
8.20
7.80
16.00
8.69
7.31
16.00
19.00
10.80
56.82
43.18
2.54
5.55
16.00
7.80
48.73
51.27
3.01
5.55
35.00
18.59
53.12
46.88
2.76
5.55
19.00
10.31
54.29
45.71
16.00
7.31
45.71
54.29
35.00
17.63
50.37
49.63
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
134
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 34
Included observations: 33
Excluded observations: 1 after adjusting endpoints
Convergence achieved after 2 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
INFLACION
-0.332864
0.003263
0.447614
0.006044
-0.743641
0.539781
0.4571
0.5893
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.454545
0.511459
8.109308
-22.58897
-22.73730
0.296679
0.585972
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
18
15
0.505650
1.490240
1.580938
1.520757
-0.684514
0.006524
Total obs
33
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 34
Included observations: 33
Excluded observations: 1 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
16
13
29
18
15
33
2
18
16
88.89
11.11
-11.11
NA
2
15
2
13.33
86.67
13.33
13.33
4
33
18
54.55
45.45
0.00
0.00
0
18
18
100.00
0.00
0
15
0
0.00
100.00
0
33
18
54.55
45.45
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
9.89
8.11
18.00
9.82
8.18
18.00
8.11
6.89
15.00
8.18
6.82
15.00
18.00
9.89
54.95
45.05
0.41
0.89
15.00
6.89
45.94
54.06
0.49
0.89
33.00
16.78
50.86
49.14
0.44
0.89
18.00
9.82
54.55
45.45
15.00
6.82
45.45
54.55
33.00
16.64
50.41
49.59
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
135
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 35 after adjusting endpoints
Convergence achieved after 5 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
V_IPC
-1.392755
0.453678
0.648239
0.222956
-2.148521
2.034829
0.0317
0.0419
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.485714
0.445026
6.535596
-18.98566
-24.24586
10.52042
0.001181
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
18
17
0.507093
1.199180
1.288057
1.229861
-0.542447
0.216953
Total obs
35
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 35 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
15
8
23
18
17
35
3
18
15
83.33
16.67
-16.67
NA
9
17
9
52.94
47.06
52.94
52.94
12
35
24
68.57
31.43
17.14
35.29
0
18
18
100.00
0.00
0
17
0
0.00
100.00
0
35
18
51.43
48.57
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
11.47
6.53
18.00
9.26
8.74
18.00
6.53
10.47
17.00
8.74
8.26
17.00
18.00
11.47
63.71
36.29
12.28
25.29
17.00
10.47
61.58
38.42
13.00
25.29
35.00
21.94
62.67
37.33
12.63
25.29
18.00
9.26
51.43
48.57
17.00
8.26
48.57
51.43
35.00
17.51
50.04
49.96
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
136
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 35 after adjusting endpoints
Convergence achieved after 5 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
PRERELA
0.386571
-0.260070
0.467725
0.226540
0.826493
-1.148012
0.4085
0.2510
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.485714
0.495735
8.109866
-22.75419
-24.24586
2.983348
0.084125
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
18
17
0.507093
1.414525
1.503402
1.445205
-0.650120
0.061523
Total obs
35
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 35 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
6
5
11
18
17
35
12
18
6
33.33
66.67
-66.67
NA
12
17
12
70.59
29.41
70.59
70.59
24
35
18
51.43
48.57
0.00
0.00
0
18
18
100.00
0.00
0
17
0
0.00
100.00
0
35
18
51.43
48.57
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
9.89
8.11
18.00
9.26
8.74
18.00
8.11
8.89
17.00
8.74
8.26
17.00
18.00
9.89
54.92
45.08
3.49
7.19
17.00
8.89
52.27
47.73
3.70
7.19
35.00
18.77
53.63
46.37
3.59
7.19
18.00
9.26
51.43
48.57
17.00
8.26
48.57
51.43
35.00
17.51
50.04
49.96
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
137
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 35 after adjusting endpoints
Convergence achieved after 5 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
D_PRECIOS
0.130911
-0.002417
0.361926
0.002160
0.361708
-1.119337
0.7176
0.2630
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.485714
0.496533
8.135990
-22.80273
-24.24586
2.886269
0.089338
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
18
17
0.507093
1.417299
1.506176
1.447979
-0.651507
0.059521
Total obs
35
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 35 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
5
5
10
18
17
35
13
18
5
27.78
72.22
-72.22
NA
12
17
12
70.59
29.41
70.59
70.59
25
35
17
48.57
51.43
-2.86
-5.88
0
18
18
100.00
0.00
0
17
0
0.00
100.00
0
35
18
51.43
48.57
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
9.86
8.14
18.00
9.26
8.74
18.00
8.14
8.86
17.00
8.74
8.26
17.00
18.00
9.86
54.79
45.21
3.36
6.91
17.00
8.86
52.13
47.87
3.55
6.91
35.00
18.72
53.49
46.51
3.45
6.91
18.00
9.26
51.43
48.57
17.00
8.26
48.57
51.43
35.00
17.51
50.04
49.96
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
138
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 35 after adjusting endpoints
Convergence achieved after 5 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
V_PRERELA
-1.358573
0.487678
0.627598
0.236546
-2.164719
2.061665
0.0304
0.0392
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.485714
0.442820
6.470945
-18.82931
-24.24586
10.83311
0.000997
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
18
17
0.507093
1.190246
1.279123
1.220926
-0.537980
0.223401
Total obs
35
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 35 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep= 0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
15
8
23
18
17
35
3
18
15
83.33
16.67
-16.67
NA
9
17
9
52.94
47.06
52.94
52.94
12
35
24
68.57
31.43
17.14
35.29
0
18
18
100.00
0.00
0
17
0
0.00
100.00
0
35
18
51.43
48.57
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
11.53
6.47
18.00
9.26
8.74
18.00
6.47
10.53
17.00
8.74
8.26
17.00
18.00
11.53
64.07
35.93
12.64
26.03
17.00
10.53
61.96
38.04
13.39
26.03
35.00
22.07
63.05
36.95
13.01
26.03
18.00
9.26
51.43
48.57
17.00
8.26
48.57
51.43
35.00
17.51
50.04
49.96
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
139
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 34
Excluded observations: 1 after adjusting endpoints
Convergence achieved after 3 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
V_TCE R
-0.141513
0.013948
0.359210
0.060502
-0.393956
0.230542
0.6936
0.8177
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.470588
0.514038
8.455532
-23.48142
-23.50815
0.053462
0.817145
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
18
16
0.506640
1.498907
1.588693
1.529526
-0.690630
0.001137
Total obs
34
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 34
Excluded observations: 1 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
18
13
31
18
16
34
0
18
18
100.00
0.00
0.00
NA
3
16
3
18.75
81.25
18.75
18.75
3
34
21
61.76
38.24
8.82
18.75
0
18
18
100.00
0.00
0
16
0
0.00
100.00
0
34
18
52.94
47.06
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
9.54
8.46
18.00
9.53
8.47
18.00
8.46
7.54
16.00
8.47
7.53
16.00
18.00
9.54
53.02
46.98
0.08
0.17
16.00
7.54
47.15
52.85
0.09
0.17
34.00
17.09
50.26
49.74
0.08
0.17
18.00
9.53
52.94
47.06
16.00
7.53
47.06
52.94
34.00
17.06
50.17
49.83
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
140
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 33
Included observations: 29
Excluded observations: 4 after adjusting endpoints
Convergence achieved after 4 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
BCCPIB
-2.313991
-0.452600
0.967141
0.200896
-2.392610
-2.252914
0.0167
0.0243
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.379310
0.429914
4.990312
-15.01974
-19.24804
8.456606
0.003637
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
18
11
0.493804
1.173775
1.268071
1.203307
-0.517922
0.219674
Total obs
29
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 33
Included observations: 29
Excluded observations: 4 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
16
5
21
18
11
29
2
18
16
88.89
11.11
-11.11
NA
6
11
6
54.55
45.45
54.55
54.55
8
29
22
75.86
24.14
13.79
36.36
0
18
18
100.00
0.00
0
11
0
0.00
100.00
0
29
18
62.07
37.93
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
12.98
5.02
18.00
11.17
6.83
18.00
5.02
5.98
11.00
6.83
4.17
11.00
18.00
12.98
72.13
27.87
10.06
26.52
11.00
5.98
54.39
45.61
16.46
26.52
29.00
18.97
65.40
34.60
12.49
26.52
18.00
11.17
62.07
37.93
11.00
4.17
37.93
62.07
29.00
15.34
52.91
47.09
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
141
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 30
Included observations: 23
Excluded observations: 7 after adjusting endpoints
Convergence achieved after 3 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
DEFICIT
-1.356079
-0.250985
0.759994
0.159829
-1.784329
-1.570339
0.0744
0.1163
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.391304
0.475995
4.757992
-13.87886
-15.39454
3.031371
0.081669
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
14
9
0.499011
1.380770
1.479509
1.405603
-0.603429
0.098456
Total obs
23
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 30
Included observations: 23
Excluded observations: 7 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
11
6
17
14
9
23
3
14
11
78.57
21.43
-21.43
NA
3
9
3
33.33
66.67
33.33
33.33
6
23
14
60.87
39.13
0.00
0.00
0
14
14
100.00
0.00
0
9
0
0.00
100.00
0
23
14
60.87
39.13
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
9.23
4.77
14.00
8.52
5.48
14.00
4.77
4.23
9.00
5.48
3.52
9.00
14.00
9.23
65.90
34.10
5.03
12.85
9.00
4.23
46.95
53.05
7.82
12.85
23.00
13.45
58.49
41.51
6.12
12.85
14.00
8.52
60.87
39.13
9.00
3.52
39.13
60.87
23.00
12.04
52.36
47.64
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
142
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 36
Convergence achieved after 3 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
PIB
-0.405862
-0.136801
0.379268
0.066392
-1.070118
-2.060509
0.2846
0.0393
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (1 df)
Probability(LR stat)
0.472222
0.477231
7.743489
-22.22712
-24.89771
5.341188
0.020827
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
19
17
0.506309
1.345951
1.433924
1.376656
-0.617420
0.107263
Total obs
36
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample: 1 36
Included observations: 36
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=
C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
15
8
23
19
17
36
4
19
15
78.95
21.05
-21.05
NA
9
17
9
52.94
47.06
52.94
52.94
13
36
24
66.67
33.33
13.89
29.41
0
19
19
100.00
0.00
0
17
0
0.00
100.00
0
36
19
52.78
47.22
Estimated Equation
Dep=0 Dep=1
Total
E(# of
Dep=0)
E(# of
Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent
Gain**
Constant Probability
Dep=0 Dep=1
Total
Constant Probability
Dep=0 Dep=1
Total
11.27
7.73
19.00
10.03
8.97
19.00
7.73
9.27
17.00
8.97
8.03
17.00
19.00
11.27
59.31
40.69
6.53
13.83
17.00
9.27
54.52
45.48
7.30
13.83
36.00
20.54
57.05
42.95
6.90
13.83
19.00
10.03
52.78
47.22
17.00
8.03
47.22
52.78
36.00
18.06
50.15
49.85
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
143
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
ANEXO III: SALIDAS EVIEWS: MODELO PARA LA ESTIMACIÓN DEL RIESGO
CAMBIARIO EN LOS PAÍSES DE EUROPA CENTRAL Y ORIENTAL
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 33
Excluded observations: 2 after adjusting endpoints
Convergence achieved after 5 iterations
Covariance matrix computed using second derivatives
Variable
Coefficient
Std. Error
z-Statistic
Prob.
C
CRED_M2
V_PRERELA
V_RES
-6.943144
0.042595
0.846114
-0.186829
2.957349
0.021514
0.369173
0.080707
-2.347759
1.979879
2.291916
-2.314896
0.0189
0.0477
0.0219
0.0206
Mean dependent var
S.E. of regression
Sum squared resid
Log likelihood
Restr. log likelihood
LR statistic (3 df)
Probability(LR stat)
0.454545
0.368571
3.939497
-13.22813
-22.73730
19.01835
0.000271
Obs with Dep=0
Obs with Dep=1
S.D. dependent var
Akaike info criterion
Schwarz criterion
Hannan-Quinn criter.
Avg. log likelihood
McFadden R-squared
18
15
0.505650
1.044129
1.225524
1.105163
-0.400852
0.418219
Total obs
33
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 33
Excluded observations: 2 after adjusting endpoints
Prediction Evaluation (success cutoff C = 0.5)
Estimated Equation
Dep=0 Dep=1
Total
P(Dep=1)<=C
P(Dep=1)>C
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent Gain**
17
1
18
17
94.44
5.56
-5.56
NA
3
12
15
12
80.00
20.00
80.00
80.00
20
13
33
29
87.88
12.12
33.33
73.33
Estimated Equation
Dep=0 Dep=1
Total
E(# of Dep=0)
E(# of Dep=1)
Total
Correct
% Correct
% Incorrect
Total Gain*
Percent Gain**
13.89
4.11
18.00
13.89
77.18
22.82
22.64
49.80
4.11
10.89
15.00
10.89
72.62
27.38
27.16
49.80
18.00
15.00
33.00
24.79
75.11
24.89
24.69
49.80
Constant Probability
Dep=0 Dep=1
Total
18
0
18
18
100.00
0.00
15
0
15
0
0.00
100.00
33
0
33
18
54.55
45.45
Constant Probability
Dep=0 Dep=1
Total
9.82
8.18
18.00
9.82
54.55
45.45
8.18
6.82
15.00
6.82
45.45
54.55
18.00
15.00
33.00
16.64
50.41
49.59
*Change in "% Correct" from default (constant probability) specification
**Percent of incorrect (default) prediction corrected by equation
144
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Dependent Variable: ENDOG
Method: ML - Binary Logit
Sample(adjusted): 1 35
Included observations: 33
Excluded observations: 2 after adjusting endpoints
Descriptive statistics for explanatory variables
Variable
Dep=0
Mean
Dep=1
All
C
CRED_M2
V_PRERELA
V_RES
1.000000
111.6819
1.545888
3.645065
1.000000
123.7336
4.122781
-2.155153
1.000000
117.1599
2.717203
1.008602
Variable
Dep=0
Standard
Deviation
Dep=1
All
C
CRED_M2
V_PRERELA
V_RES
0.000000
26.87420
1.119799
6.028355
0.000000
25.54303
3.843192
12.54704
0.000000
26.57559
2.970844
9.837823
Observations
18
15
33
1.0
0.8
0.6
0.4
0.2
0.0
1.0
0.5
0.0
-0.5
-1.0
5
10
Error
15
20
Real
145
25
30
Estimada
35
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
146
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
ANEXO IV: SALIDAS SPSS: ANÁLISIS DE LA VARIANZA
Informe
Variación mensual de las reservas
Media
Probabilidad
de crisis
N
Desv. típ.
,00
3,3070
19
6,0410
1,00
-2,1552
15
12,5470
Total
,8972
34
9,7094
Tabla de ANOVA
Suma de
cuadrados
Variación mensual de lasInter-grupos (Combinadas)
reservas * Probabilidad Intra-grupos
de crisis
Total
Media
cuadrática
gl
250,092
1
250,092
2860,869
32
89,402
3110,961
33
F
2,797
Sig.
,104
Informe
Reservas sobre oferta monetaria (%)
Media
Probabilidad
de crisis
N
Desv. típ.
,00
57,8384
19
94,3451
1,00
34,0441
15
84,8647
Total
47,3409
34
89,7458
Tabla de ANOVA
Suma de
cuadrados
Reservas sobre oferta
monetaria (%) *
Probabilidad de crisis
Media
cuadrática
gl
4745,815
1
4745,815
Intra-grupos
261046,339
32
8157,698
Total
265792,155
33
Inter-grupos (Combinadas)
147
F
,582
Sig.
,451
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Informe
Nivel de reservas internacionales
Media
Probabilidad
de crisis
N
Desv. típ.
,00
5339,0707
19
5102,2591
1,00
2282,4827
16
2921,6362
Total
3941,7733
35
4464,8382
Tabla de ANOVA
Nivel de reservas
internacionales *
Probabilidad de crisis
Inter-grupos
Suma de
cuadrados
81148286,326
(Combinadas)
1
Media
cuadrática
81148286,326
18079825,228
gl
Intra-grupos
596634232,537
33
Total
677782518,863
34
F
4,488
Sig.
,042
Informe
Variación mensual del crédito interno
Probabilidad
de crisis
,00
Media
1,5159
N
19
Desv. típ.
2,1585
1,00
2,0129
15
6,8304
Total
1,7352
34
4,7326
Tabla de ANOVA
Suma de
cuadrados
Variación mensual del
crédito interno *
Probabilidad de crisis
Media
cuadrática
gl
2,070
1
2,070
Intra-grupos
737,032
32
23,032
Total
739,103
33
Inter-grupos (Combinadas)
F
,090
Sig.
,766
Informe
Crédito interno sobre la oferta monetaria
Media
Probabilidad
de crisis
N
Desv. típ.
,00
113,4005
19
27,1701
1,00
126,3921
16
26,8707
Total
119,3395
35
27,4314
Tabla de ANOVA
Suma de
cuadrados
Crédito interno sobre la Inter-grupos (Combinadas)
oferta monetaria *
Intra-grupos
Probabilidad de crisis
Total
148
Media
cuadrática
gl
1466,006
1
1466,006
24118,361
33
730,859
25584,367
34
F
2,006
Sig.
,166
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Informe
Variación anual del IPC
Probabilidad
de crisis
,00
Media
40,9289
N
18
Desv. típ.
52,8959
1,00
52,0878
15
67,8827
Total
46,0011
33
59,4499
Tabla de ANOVA
Suma de
cuadrados
Inter-grupos (Combinadas)
Variación anual del IPC *
Intra-grupos
Probabilidad de crisis
Total
Media
cuadrática
gl
1018,805
1
1018,805
112078,565
31
3615,438
113097,370
32
F
Sig.
,282
,599
F
Sig.
Informe
Variación mensual del IPC
Media
Probabilidad
de crisis
N
Desv. típ.
,00
1,7748
18
1,1644
1,00
6,2998
17
6,5808
Total
3,9727
35
5,1306
Tabla de ANOVA
Suma de
cuadrados
Variación mensual del
IPC * Probabilidad de
crisis
Media
cuadrática
gl
Inter-grupos (Combinadas)
179,014
1
179,014
Intra-grupos
715,966
33
21,696
Total
894,979
34
8,251
,007
Informe
Precios relativos respecto al IPC alemán
Media
Probabilidad
de crisis
N
Desv. típ.
,00
3,5668
18
7,1279
1,00
1,1636
17
1,5375
Total
2,3995
35
5,2916
Tabla de ANOVA
Suma de
cuadrados
Inter-grupos (Combinadas)
Precios relativos
respecto al IPC alemán * Intra-grupos
Probabilidad de crisis
Total
149
Media
cuadrática
gl
50,496
1
50,496
901,542
33
27,319
952,038
34
F
1,848
Sig.
,183
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Informe
Diferencial de precios respecto al IPC alemán
Probabilidad
de crisis
,00
Media
270,0227
N
18
Desv. típ.
745,6710
1,00
21,5452
17
157,4272
Total
149,3336
35
552,7672
Tabla de ANOVA
Suma de
cuadrados
539793,341
1 539793,341
9848961,649
33 298453,383
Inter-grupos (Combinadas)
Diferencial de precios
respecto al IPC alemán *Intra-grupos
Probabilidad de crisis
Total
Media
cuadrática
gl
10388754,990
F
Sig.
1,809
,188
34
Informe
Variación mensual de los precios relativos
Probabilidad
de crisis
,00
Media
1,5459
N
18
Desv. típ.
1,1198
1,00
5,9979
17
6,4793
Total
3,7083
35
5,0477
Tabla de ANOVA
Inter-grupos
Variación mensual de los
precios relativos *
Intra-grupos
Probabilidad de crisis
Total
Suma de
cuadrados
173,286
(Combinadas)
1
Media
cuadrática
173,286
693,024
33
21,001
866,309
34
gl
F
8,251
Informe
Variación mensual del tipo de cambio efectivo real
Media
Probabilidad
de crisis
N
Desv. típ.
,00
1,4733
18
1,9212
1,00
1,9267
16
8,3496
Total
1,6867
34
5,8002
Tabla de ANOVA
Suma de
cuadrados
Variación mensual del
tipo de cambio efectivo
real * Probabilidad de
crisis
Media
cuadrática
gl
1,742
1
1,742
Intra-grupos
1108,472
32
34,640
Total
1110,213
33
Inter-grupos (Combinadas)
150
F
,050
Sig.
,824
Sig.
,007
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
Informe
Balanza por cuenta corriente (% PIB)
Media
Probabilidad
de crisis
N
Desv. típ.
,00
-2,0091
18
3,8896
1,00
-5,6275
11
3,0943
Total
-3,3816
29
3,9746
Tabla de ANOVA
Suma de
cuadrados
Balanza por cuenta
corriente (% PIB) *
Probabilidad de crisis
Media
cuadrática
gl
89,391
1
89,391
Intra-grupos
352,933
27
13,072
Total
442,324
28
Inter-grupos (Combinadas)
F
6,839
Sig.
,014
Informe
Déficit Público (% PIB)
Media
Probabilidad
de crisis
N
Desv. típ.
,00
-2,5023
14
2,7553
1,00
-4,8662
9
3,8079
Total
-3,4273
23
3,3392
Tabla de ANOVA
Suma de
cuadrados
30,611
1
30,611
Intra-grupos
214,690
21
10,223
Total
245,301
22
Inter-grupos (Combinadas)
Déficit Público (% PIB)
* Probabilidad de crisis
Media
cuadrática
gl
F
2,994
Sig.
,098
Informe
Crecimiento anual del PIB
Media
Desv. típ.
19
3,728
1,00
-4,805
17
7,877
Total
-2,315
36
6,420
,00
Probabilidad
de crisis
N
-8,764E-02
Tabla de ANOVA
Suma de
cuadrados
Crecimiento anual del
PIB * Probabilidad de
crisis
Media
cuadrática
gl
199,685
1
199,685
Intra-grupos
1242,955
34
36,558
Total
1442,640
35
Inter-grupos (Combinadas)
151
F
5,462
Sig.
,025
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
ANEXO V: DATOS MUESTRALES
PAÍS
BULGARIA
ESLOVENIA
HUNGRÍA
POLONIA
REP. CHECA
REP. ESLOVACA
RUMANIA
RUSIA
UCRANIA
PERIODO
V_TC
ENDOG
V_RES
RES_M2
V_CRED
CRED_M2
Ene.92 – Ago.93
0.801
0
25,32
14,87
6,96
167,08
Mar.94 – Sep.94
31.493
1
-11,18
8,81
0,43
179,03
Abr.95 – Oct.95
0.425
0
3,99
19,23
0,40
119,32
May.96 – Feb.97
43.991
1
-12,55
9,58
-1,30
121,69
Sep.97 - Jun.00
0.008
0
1,46
76,89
-0,73
75,91
Feb.92
23.191
1
11,11
5,86
-3,21
108,43
Sep.92 – Jun.00
0.721
0
1,91
33,10
1,42
94,47
Ene.92 – Ago.94
1.092
0
1,82
357,92
0,63
142,30
Mar.95
10.941
1
-1,34
338,79
1,37
140,44
Oct.95 – Jun.00
0.657
0
0,48
279,33
0,56
138,42
Mar.92
10.899
1
-3,53
14,64
13,57
108,05
Oct.92 – Feb.93
0.517
0
-1,97
15,03
0,72
106,01
Sep.93
10.698
1
-0,24
12,59
-0,01
111,70
Abr.94 – Jun.00
0.687
0
2,36
36,27
0,93
96,95
Ene. 92 – Jul.98
-0.021
0
3,31
24,95
0,82
103,23
Sep.99 – Jun.00
-0.125
0
0,99
34,80
-0,78
91,08
Ene.92 – Mar.98
0.120
0
6,94
19,14
0,78
104,22
May.99 – Jun.00
-0.421
0
3,61
25,51
0,38
101,33
May.92 – Ago.92
14.590
1
13,17
5,27
-12,79
116,41
Mar.93 – Mar.94
14.449
1
-0,48
19,37
7,98
104,03
Oct.94 – Abr.95
2.841
0
0,16
34,38
5,42
88,96
Nov.95
10.420
1
-6,96
21,51
2,99
96,68
Ene.97 – Feb.97
28.536
1
9,20
26,34
2,76
106,05
Sep.97 – Ago.98
1.647
0
0,06
45,70
2,48
85,08
Mar.99
11.223
1
1,25
32,33
-1,62
91,30
Oct.99 – Jun.00
1.494
0
0,96
37,48
-0,68
76,04
Jul.92 – Jun.95
28.516
1
-
-
-
-
Ene.96 – Feb.98
-0.026
0
-0,32
20,64
2,07
144,57
Sep.98 – Ene.99
126.101
1
-0,33
15,91
-1,43
157,33
Ago.99 – Jun.00
0.465
0
8,09
23,52
0,06
144,40
Ene.93 – Dic.93
14.068
1
-
-
-
166,27
Jun.94 – Oct.95
26.086
1
-31,76
-0,47
15,69
114,30
May.96 – Feb.98
-0.610
0
6,42
0,14
2,14
130,88
Sep.98 – Oct.98
34.019
1
-15,71
-0,25
4,35
149,37
Ago.99
14.118
1
17,02
0,38
1,41
151,20
Mar.00 – Jun.00
-0.995
0
-2,78
0,04
5,23
144,33
152
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
PAÍS
BULGARIA
ESLOVENIA
HUNGRÍA
POLONIA
REP. CHECA
REP. ESLOVACA
RUMANIA
RUSIA
UCRANIA
PERIODO
INFLACION
V_TCER
BCCPIB
DEFICIT
PIB
V_IPC
Ene.92 – Ago.93
99,93
4,54
-4,17
-4,93
-7,30
4,73
Mar.94 – Sep.94
60,55
-3,75
-10,13
-12,09
-1,50
4,08
Abr.95 – Oct.95
57,83
0,64
-0,33
-4,66
1,70
1,81
May.96 – Feb.97
27,92
-1,67
-0,20
-5,25
2,20
2,15
Sep.97 - Jun.00
209,88
0,28
-0,54
2,03
-0,33
0,64
-
14,73
-
-
-8,90
13,71
Sep.92 – Jun.00
15,04
1,57
0,99
-0,37
2,82
1,01
Ene.92 – Ago.94
21,62
0,32
-5,05
-5,72
-1,85
1,67
Mar.95
22,31
0,34
-9,77
-7,12
2,90
2,68
Oct.95 – Jun.00
16,88
0,10
-4,13
-6,48
3,28
1,21
Mar.92
53,22
1,71
-2,52
-
-6,97
4,21
Oct.92 – Feb.93
43,79
1,83
-3,14
-
2,60
3,04
Sep.93
36,50
-0,55
-5,32
-
3,80
1,60
Abr.94 – Jun.00
18,36
0,39
-1,84
-1,78
5,65
1,28
Ene. 92 – Jul.98
9,52
0,35
-3,06
0,20
0,88
0,77
Sep.99 – Jun.00
4,10
-0,37
-3,45
-1,04
-0,50
0,36
Ene.92 – Mar.98
8,76
0,21
-4,10
-
2,41
0,75
May.99 – Jun.00
12,88
1,26
-5,68
-
1,00
1,47
May.92 – Ago.92
243,27
7,43
-3,51
1,94
-12,92
8,92
Mar.93 – Mar.94
177,50
15,07
-7,69
-4,68
-8,70
10,89
Oct.94 – Abr.95
57,66
4,89
-1,51
-2,51
3,90
2,18
Nov.95
25,99
4,39
-5,02
-2,96
7,10
2,03
Feb.92
Ene.97 – Feb.97
49,84
10,97
-7,34
-4,04
3,90
6,49
Sep.97 – Ago.98
102,80
5,19
-6,12
-3,89
-6,10
3,55
Mar.99
37,06
8,86
-7,03
-2,82
-5,40
2,69
Oct.99 – Jun.00
53,42
4,33
-3,83
0,24
-3,90
3,22
Jul.92 – Jun.95
17,57
-
-
-
-19,40
17,57
Ene.96 – Feb.98
1,86
1,06
1,47
-5,96
-2,23
1,86
Sep.98 – Ene.99
1,31
-0,83
-3,37
-6,77
-4,50
1,31
Ago.99 – Jun.00
1,32
-1,03
11,01
-0,15
3,20
1,32
Ene.93 – Dic.93
23,17
-18,53
-
-
-17,00
23,17
Jun.94 – Oct.95
5,63
-4,14
-
-
-14,20
5,63
May.96 – Feb.98
1,07
0,92
-2,67
-
-6,50
1,07
Sep.98 – Oct.98
-0,53
-0,89
-
-
-1,70
-0,53
Ago.99
-
-2,31
-
-
-0,40
0,50
Mar.00 – Jun.00
-
-
-
-
-0,40
-
153
Crisis Cambiarias y Crisis de Balanza de Pagos: Modelos de Primera Generación.
Aplicación al caso de Europa Central y Oriental
PAÍS
BULGARIA
ESLOVENIA
HUNGRÍA
POLONIA
REP. CHECA
REP. ESLOVACA
RUMANIA
RUSIA
UCRANIA
PERIODO
D_PRECIOS
PRERELA
V_PRERELA
N_RES
Ene.92 – Ago.93
-70,44
0,24
4,35
860,33
Mar.94 – Sep.94
-57,07
0,41
3,54
616,67
Abr.95 – Oct.95
0,19
1,00
1,71
1434,43
May.96 – Feb.97
19,00
1,19
1,91
710,67
Sep.97 - Jun.00
3112,42
30,75
0,59
2546,88
-52,25
0,42
13,08
6,72
Sep.92 – Jun.00
7,10
1,06
0,84
0,72
Ene.92 – Ago.94
-31,11
0,67
1,36
5451,16
Mar.95
-11,10
0,89
2,37
6830,33
Oct.95 – Jun.00
51,11
1,49
1,08
9537,93
Mar.92
-53,27
0,41
3,79
3518,97
Oct.92 – Feb.93
-42,50
0,54
2,40
3946,02
Sep.93
-37,00
0,61
1,36
3378,53
Abr.94 – Jun.00
29,23
1,28
1,15
17952,29
Ene. 92 – Jul.98
3,24
1,03
0,61
7422,07
Sep.99 – Jun.00
29,99
1,28
0,18
12709,90
Ene.92 – Mar.98
-1,05
0,99
0,59
2100,29
May.99 – Jun.00
31,93
1,30
1,08
3010,45
May.92 – Ago.92
-83,93
0,08
8,39
440,67
Mar.93 – Mar.94
-78,27
0,17
9,91
789,67
Oct.94 – Abr.95
-8,36
0,92
2,01
1947,57
Nov.95
2,80
1,03
2,07
1494,00
Feb.92
Ene.97 – Feb.97
63,70
1,63
6,41
2073,33
Sep.97 – Ago.98
394,93
4,79
3,49
3462,42
Mar.99
549,33
6,27
2,62
2670,00
Oct.99 – Jun.00
893,05
9,45
3,10
2651,33
Jul.92 – Jun.95
-90,83
0,01
17,18
-
Ene.96 – Feb.98
43,20
1,42
1,13
13369,53
Sep.98 – Ene.99
71,47
1,68
1,22
11054,40
Ago.99 – Jun.00
313,37
3,97
1,22
10321,98
Ene.93 – Dic.93
-92,16
0,00
22,95
468,80
Jun.94 – Oct.95
-82,47
0,16
5,45
31,60
May.96 – Feb.98
104,09
2,01
0,95
1850,00
Sep.98 – Oct.98
120,87
2,15
-0,63
1530,03
Ago.99
177,43
2,69
0,34
905,33
-
-
-
867,05
Mar.00 – Jun.00
154