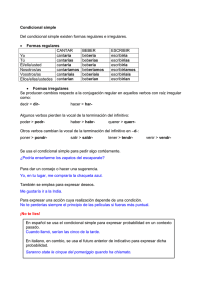
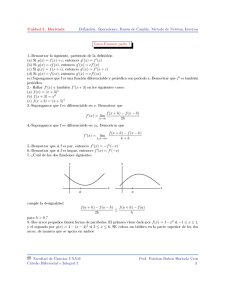
Muestra que si P A! > P B!, entonces P A \ B! > P B \ A
Anuncio

Muestra que si P (A) > P (B), entonces P (A j B) > P (B j A). Solución: Primeramente recordemos la de…nición de la probabilidad condicional: La probabilidad condicional del evento A; dado el evento B, denotada como P (A j B), se de…ne como P (A j B) = P (A \ B) P (B) donde necesariamente P (B) > 0 es Dada está de…nición, es obvio que la probabilidad condicional del evento B; dado el evento A, denotada como P (B j A), P (B j A) = P (A \ B) P (A) con P (A) > 0 Pasemos ahora a nuestro problema: Como P (A) > P (B) se tiene 1 1 > P (B) P (A) y desde luego P (A \ B) P (A \ B) > P (B) P (A) pero, por la de…nición de la probabilidad condicional P (A j B) = P (A \ B) P (B) y P (B j A) = P (A \ B) P (A) así que …nalmente P (A j B) > P (B j A) 1