ANOVA II CON INTERACCIÓN

Estadística Ciencias Ambientales
Facultad de Ciencias
Departamento de Matemáticas
Profesor: Santiago de la Fuente Fernández
ANÁLISIS VARIANZA MULTIFACTORIAL
ANOVA II CON INTERACCIÓN
ANÁLISIS DE LA VARIANZA CON DOS FACTORES E INTERACCIÓN
Modelo:
yij ≡
yij = μ + α i + β j + (α β ) ij + U
i = 1, 2, L , I
j = 1, 2, L , J
representa la respuesta de la variable en el i-ésimo nivel del FACTOR 1
( )
μ ij = E yij = μ + α i + β j + (α β ) ij
es el valor medio de
(α )
y en el jésimo nivel del FACTOR 2
yij
αi ≡
representa el efecto que sobre la media global
μ
tiene en el NIVEL i el FACTOR 1
(α )
βj ≡
representa el efecto que sobre la media global
μ
tiene en el NIVEL j el FACTOR 2
(β )
(α β ) ij
U ≡
≡
representa el efecto de la interacción entre el NIVEL i del FACTOR 1
es la variación aleatoria de las
Supondremos que
U
yij
(α )
y el NIVEL j del FACTOR 2
(igual para todas).
sigue una distribución
(β )
N (0, σ ) , lo que implica que yij
sigue una distribución
I
J
I
J
i=1
j =1
i=1
j=1
∑ α i = ∑ β j = ∑ (α β ) ij = ∑ (α β ) ij = 0
(
N μij, σ
)
(β )
Niveles
1
2
y111
y112
FACTOR 1 (α)
1
.........
.........
y211
y221
.........
.........
y21 n
21
.........
y22 n
22
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
.........
y1J1
y1J2
.........
.........
y1J n
y2J1
y 1• •
1J
y2J2
.........
.........
y2J n
2J
.........
.........
y 2• •
.........
.........
yIJ1
yI21
yI22
.........
.........
yI1 n
.........
.........
yI2 n
y •1 •
y •2•
I1
Medias
columnas
y222
.........
.........
.........
.........
12
.........
yI11
yI12
I
y121
y122
.........
.........
y12 n
11
Medias
Filas
J
.........
.........
y11 n
y212
2
(β )
I2
.........
.........
.........
.........
yIJ2
.........
.........
yIJ n
y I••
y •J•
y •••
IJ
Muestra aleatoria nij observaciones casilla (i, j)
FACTOR 2
(
yijk ∈ N μ + αi + β j + (α β )ij ; σ2
El origen de la descomposición de la varianza total, donde
( yijk − y••• )
=
( yijk − yij• )
)
independientes
k = n ij
(α β )
βˆ
ij
6444474
4448
647
4α i 48
4
647
4 j 48
4
+ yij• − yi • • − y• j• + y• • • + ( yi • • − y• • • ) + y• j• − y• • •
(
ˆ
)
(
)
SCT
I J K −1
64444744448
I
J
I
K
∑∑∑ ( yijk − y••• )
2
i =1 j=1 k =1
=
J
K
2
(
)
−
y
y
ijk
ij
•
∑∑∑
+
i =1 j=1 k =1
1
444424444
3
SCR
I J ( K −1)
I
+
J
K
∑∑∑ ( y
ij•
− yi • • − y• j• + y• • •
)
2
i =1 j=1 k =1
1
444444424444444
3
SCE (αβ )
( I −1)( J −1)
operando, resulta:
I
+
J
K
∑∑∑ ( y
i••
− y••• )
I
2
i =1 j=1 k =1
1
4444244443
SCE (α )
I −1
+
J
K
∑∑∑ ( y
• j•
− y•••
)2
i =1 j=1 k =1
1
4444244443
SCE (β )
J −1
SCT
I J K −1
64444744448
I
J
K
2
(
)
y
−
y
ijk
•
•
•
∑∑∑
=
i = 1 j = 1 k =1
I
J
K
∑∑∑ ( y
ijk
− y ij•
)
I
2
i = 1 j = 1 k =1
1
444424444
3
SCR
I J ( K −1)
+ k
J
∑∑ ( y
ij•
− y i • • − y • j• + y • • •
)
I
2
i =1 j = 1
1
44444424444443
SCE (αβ )
( I −1)( J −1)
SCT = SCR + SCE (α β ) + SCE (α ) + SCE (β )
SCT ≡ Variabilidad total de todos los datos
SCR ≡ Variabilidad debida a los factores
SCE (α β ) ≡ Variabilidad debida a las interacciones
SCE (α ) ≡ Variabilidad debida a los distintos niveles del Factor 1
SCE (β ) ≡ Variabilidad debida a los distintos niveles del Factor 2
+ JK
∑( y
i••
− y••• )
J
2
1 424443
14i =4
SCE (α )
I −1
+ IK
∑(y
• j•
− y•••
)2
j=1
1
44
42444
3
SCE (β )
J −1
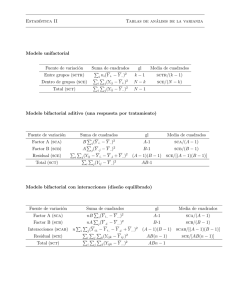
TABLA ANOVA: ANÁLISIS ESTADÍSTICO
Fuente
variación
Factor
Factor
(α )
(β )
Suma cuadrados
SCE (α ) = J K
SCE (β ) = I K
Interacción
=K
∑( y
− y••• )
i =1
J
∑(y
• j•
− y•••
)
2
∑∑ ( yij• − yi•• − y• j• + y••• ) 2
SCR =
( I −1 )
Ŝα2
SCE (α )
=
( I −1 )
( J −1 )
Ŝβ2
SCE (β )
=
( J −1)
( I −1 ) ( J −1)
J
i =1 j = 1
I
J
Residual
i••
2
K
2
(
)
y
−
y
•
ijk
ij
∑∑∑
I J (K − 1)
i =1 j=1 k =1
I
Total
SCT =
Varianza
j =1
SCE (α β ) =
I
I
grados libertad
J
K
∑∑∑ ( y
ijk
− y•••
)2
Ŝα2 β
SCE (α β )
=
( I − 1 )( J − 1 )
Ŝ2r =
Test F
Fα =
Fβ =
Fα β =
SCR
IJ( k −1)
IJ K −1
i =1 j=1 k =1
ANÁLISIS ESTADÍSTICO: Contraste del Efecto de cada factor
H o : α1 = α 2 = L = α I = 0
H o : β1 = β 2 = L = β J = 0
H1 : A lgún α i ≠ 0
H1 : A lgún β j ≠ 0
EL FACTOR 1
(α )
NO INFLUYE
EL FACTOR 2
(β )
NO INFLUYE
H o : (α β ) i j = 0
∀ i, j
H1 : Algún (α β ) i j ≠ 0
NO HAY INTERACCIONES
Ŝα2
Ŝ2r
Ŝβ2
Ŝ2r
2
Ŝαβ
Ŝ2r
ESTADÍSTICOS DE CONTRASTE:
H o : α1 = α 2 = L = α I = 0
H o : β1 = β 2 = L = β J = 0
H1 : A lgún α i ≠ 0
H1 : A lgún β j ≠ 0
EL FACTOR 1
(α )
NO INFLUYE
Se acepta la hipótesis nula cuando:
Ŝα2
Fα = 2 ≤ Fα, (I −1), I J (K −1)
Ŝr
EL FACTOR 2
(β )
H o : (α β ) i j = 0
∀ i, j
H1 : Algún (α β ) i j ≠ 0
NO INFLUYE
Se acepta la hipótesis nula cuando:
Ŝβ2
Fβ = 2 ≤ Fα, (J −1), I J (K −1)
Ŝr
NO HAY INTERACCIONES
Se acepta la hipótesis nula cuando:
Ŝα2 β
Fα β = 2 ≤ Fα, (I −1)(J −1), I J (K −1)
Ŝr
Cuando se rechaza la hipótesis nula Ho se pueden hacer pruebas simultáneas entre todas las posibles parejas de niveles en cada
factor. Uno de los tests más empleados en las Pruebas Post hoc es el Test de Bonferroni.
CONDICIONES DEL ANÁLISIS ESTADÍSTICO ANOVA
•
NORMALIDAD .- Los datos obtenidos en cada nivel de los factores se ajustan razonablemente a una distribución normal.
-
yij
sigue una distribución normal
(
N μ ij , σ
)
∀ i, j -
•
HOMOCEDASTICIDAD.- La variabilidad de los datos en cada nivel de los factores es similar (contraste de igualdad de
2
∀ i, j
varianzas) - σ = Var y ij
•
LINEALIDAD.- Los residuos (diferencia de los datos a su media, en cada nivel de los factores) se distribuyen alrededor del cero.
•
INDEPENDENCIA.- Las observaciones se realizan de forma independiente unas de otras (diseño de la obtención de datos).
( )
E (U ) = 0
En caso de existir desviaciones significativas sobre estos requisitos, los resultados posteriores pueden ser incorrectos.
EYSENCK (1974).- En un estudio sobre memoria verbal se seleccionaron al azar 50 personas mayores y 50 jóvenes (Factor 1: Edad).
Dentro de cada uno de estos grupos se asignaron, al azar, 10 personas a 5 distintos grupos a los que se les presentó una misma lista
de 27 palabras. A cada uno de los 5 grupos se les dieron las siguientes instrucciones (Factor 2: Método).
Grupo 1 (Contar): Se les pidió que contasen el número de letras de cada palabra. Grupo 2 (Rimar): Se les pidió que rimasen cada
palabra con otra. Grupo 3 (Adjetivar). Se les pidió que a cada palabra le asignasen un adjetivo. Grupo 4 (Imaginar): Se les pidió que a
cada palabra le asignasen una imagen. Grupo 5 (Recordar):Se les pidió que memorizasen las palabras.
I=2
J=5
K = 10
Factor 1 (Edad)
Mayores
I=2
Jóvenes
Contar
9
8
6
8
10
4
6
5
7
7
8
6
4
6
7
6
5
7
9
7
FACTOR 2 (Método) J = 5
Rimar
Adjetivar
Imaginar
12
11
7
11
13
9
16
8
6
11
6
6
9
14
6
23
11
11
12
13
6
10
13
3
19
10
8
11
11
7
20
14
10
16
11
7
16
18
8
15
14
10
18
13
4
16
22
7
20
17
10
22
16
6
14
12
7
19
11
7
Recordar
10
19
14
5
10
11
14
15
11
11
21
19
17
15
22
16
22
22
18
21
K = 10
A los 4 primeros grupos no se les dijo que deberían recordar las palabras. Finalmente, tras revisar la lista 3 veces, se recogió el
número de palabras recordadas por cada grupo (variable respuesta).
Factor 1 (Edad)
I=2
J=5
K = 10
FACTOR 2 (Método) J = 5
Adjetivar
Imaginar
Recordar
Contar
Rimar
Mayores
I=1
y11• = 7
y12 • = 6,9
y13• = 11
y14• = 13,4
y15• = 12
y1• • = 10,06
Jóvenes
I=2
y 21• = 6,5
y 22 • = 7 ,6
y 23• = 14,8
y 24• = 17,6
y 25• = 19,3
y 2• • = 13,16
medias por
columnas
y •1• = 6,75
y • 2 • = 7 , 25
y • 3• = 12 ,9
y • 4 • = 15,5
y • • • = 11,61
σ •2• • = 2667 ,79
s •2• • = 2694 ,74
medias por filas
y • 5 • = 15,65
SCT = 2694 ,74
y • • • = 11,6
( yi•• − y••• ) 2 = 5 .10 ∑ ( yi•• − y••• ) 2 = 50 [ ( 10,06 − 11,61 ) 2 + ( 13,16 − 11,61 ) 2 ] = 240,25
∑
i =1
i =1
I
SCE (α ) = J K
SCE (β ) = I K
2
J
∑ ( y• j• − y••• )
2
= SCE (β ) = 2 .10
j =1
5
2
(
)
y
−
y
=
j
•
•
•
•
•
∑
j=1
20
{( 6,75 − 11,61 )
2
+ ( 7,25 − 11,61 ) 2 +
}
+ ( 12,9 − 11,61 ) 2 + ( 15,5 − 11,61 ) 2 + ( 15,65 − 11,61 ) 2 = 1514,94
SCE (α β ) = K
= 10
I
J
( yij• − yi•• − y• j• + y••• )
∑∑
i =1 j = 1
{ (7 − 10,06 − 6,75 + 11,61)
2
2
2
= 10
5
( yij• − yi•• − y• j• + y••• ) 2 =
∑∑
i =1 j=1
+ (6,5 − 13,16 − 6,75 + 11,61) 2 + (6,9 − 10,6 − 7,25 + 11,61) 2 +
+ (7,6 − 13,16 − 7,25 + 11,61) 2 + (11 − 10,06 − 12,9 + 11,61) 2 + (14,8 − 13,16 − 12,9 + 11,61) 2 +
+ (13,4 − 10,06 − 15,5 + 11,61) 2 + (17,6 − 13,16 − 15,5 + 11,61) 2 + (12 − 10,06 − 15,65 + 11,61) 2 +
}
+ (19,3 − 13,16 − 15,65 + 11,61) 2 = 10 . 19,03 = 190,3
SCT = SCR + SCE (α β ) + SCE (α ) + SCE (β ) a SCR = SCT − SCE (α β ) − SCE (α ) − SCE (β )
SCR = SCT − SCE (α β ) − SCE (α ) − SCE (β ) ⇒ SCR = 2694,74 − 204,25 − 1514,94 − 190,3 = 785,25
TABLA ANOVA: ANÁLISIS ESTADÍSTICO
Fuente
variación
Suma cuadrados
Factor
(α )
SCE (α ) = 204,25
Factor
(β )
SCE (β ) = 1514,94
Interacción
SCE (α β ) = 190.3
Residual
SCR = 785,25
Total
SCT = 2694,74
grados libertad
Varianza
240,25
= 240,25
( I −1)
1514,94
Ŝβ2 =
= 378,74
J −1= 4
4
( I − 1 ) ( J − 1 ) = 4 Ŝα2 β = 190,3 = 47,58
4
785,25
Ŝ2r =
= 8,725
I J (K − 1) = 90
90
I −1= 1
Ŝα2 =
I J K − 1 = 99
SCT ≡ 2694,74 (Variabilidad total de todos los datos)
SCR ≡ 785,25 (Variabilidad debida a los factores)
SCE (α β ) ≡ 190,3 (Variabilidad debida a las interacciones)
SCE (α ) ≡ 204,25 (Variabilidad debida a los distintos niveles del Factor 1)
SCE (β ) ≡ 1514,94 (Variabilidad debida a los distintos niveles del Factor 2)
Test F
240,25
= 27,54
8,725
378,74
Fβ =
= 43,41
8,725
47,58
Fα β =
= 5,45
8,725
Fα =
ANÁLISIS ESTADÍSTICO: Contraste del Efecto de cada factor
H o : α1 = α 2 = L = α I = 0
H o : β1 = β 2 = L = β J = 0
H1 : A lgún α i ≠ 0
H1 : A lgún β j ≠ 0
EL FACTOR 1
(α )
NO INFLUYE
EL FACTOR 2
(β )
NO INFLUYE
H o : (α β ) i j = 0
∀ i, j
H1 : Algún (α β ) i j ≠ 0
NO HAY INTERACCIONES
ESTADÍSTICOS DE CONTRASTE:
H o : α1 = α 2 = L = α I = 0
H o : β1 = β 2 = L = β J = 0
H1 : A lgún α i ≠ 0
H1 : A lgún β j ≠ 0
EL FACTOR 1
(α )
NO INFLUYE
Se acepta la hipótesis nula cuando:
Ŝα2
Fα = 2 ≤ Fα, (I −1), I J (K −1)
Ŝr
Fα =
Ŝα2
Ŝr2
= 27,54 > 3,96 = F0,05, 1, 90
EL FACTOR 2
(β )
NO INFLUYE
Se acepta la hipótesis nula cuando:
Ŝβ2
Fβ = 2 ≤ Fα, (J −1), I J (K −1)
Ŝr
Fβ =
Ŝβ2
Ŝ2r
= 43,41 > 2,49 = F0,05, 4, 90
Se rechazan todas las hipótesis nulas. En consecuencia, influyen los factores.
H o : (α β ) i j = 0
∀ i, j
H1 : Algún (α β ) i j ≠ 0
NO HAY INTERACCIONES
Se acepta la hipótesis nula cuando:
Ŝα2 β
Fα β = 2 ≤ Fα, (I −1)(J −1), I J (K −1)
Ŝr
Fαβ =
2
Ŝαβ
Ŝ2r
= 5,45 > 2,49 = F0,05, 4, 90
Se verifica que la diferencia de medias es significativa, con una significación de 0,05