Tema 4. Análisis descriptivo de series cronológicas

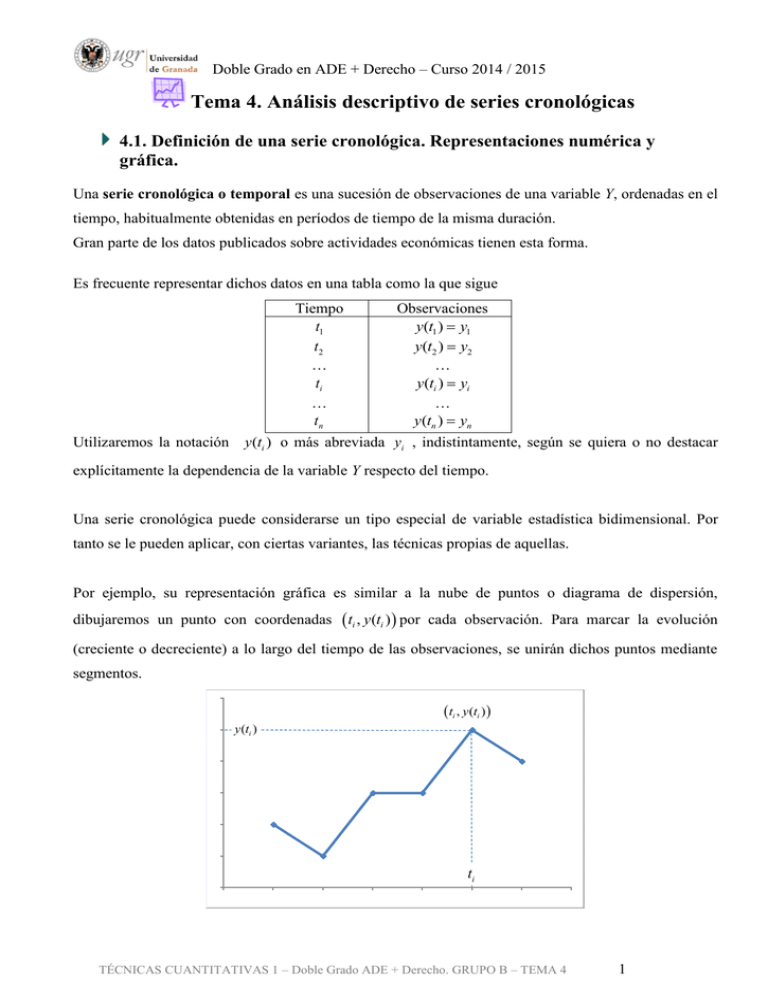
Doble Grado en ADE + Derecho – Curso 2014 / 2015
Tema 4. Análisis descriptivo de series cronológicas
4.1. Definición de una serie cronológica. Representaciones numérica y
gráfica.
Una serie cronológica o temporal es una sucesión de observaciones de una variable Y, ordenadas en el
tiempo, habitualmente obtenidas en períodos de tiempo de la misma duración.
Gran parte de los datos publicados sobre actividades económicas tienen esta forma.
Es frecuente representar dichos datos en una tabla como la que sigue
Tiempo
t1
t2
…
ti
…
tn
Utilizaremos la notación
Observaciones
y(t1 )  y1
y(t2 )  y2
…
y(ti )  yi
…
y(tn )  yn
y (ti ) o más abreviada yi , indistintamente, según se quiera o no destacar
explícitamente la dependencia de la variable Y respecto del tiempo.
Una serie cronológica puede considerarse un tipo especial de variable estadística bidimensional. Por
tanto se le pueden aplicar, con ciertas variantes, las técnicas propias de aquellas.
Por ejemplo, su representación gráfica es similar a la nube de puntos o diagrama de dispersión,
dibujaremos un punto con coordenadas
 ti , y(ti )  por
cada observación. Para marcar la evolución
(creciente o decreciente) a lo largo del tiempo de las observaciones, se unirán dichos puntos mediante
segmentos.
6
 ti , y(ti ) 
y (ti )
5
4
3
2
1
ti
0
0
1
2
3
4
5
6
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
7
1
Doble Grado en ADE + Derecho – Curso 2014 / 2015
Si dentro de cada período de tiempo ti se tienen varias observaciones, los datos se representan en una
tabla como la siguiente (por ejemplo, observaciones mensuales, trimestrales, … en cada año)
Año/estaciones
t1
…
ti
…
tn
1
y11
…
yi1
…
yn1
…
…
…
…
…
…
j
y1 j
…
yij
…
ynj
…
…
…
…
…
…
S
y1s
…
yis
…
yns
►PRACTICA 4.1. Consultar en INEbase la evolución del número de parados en España y
representar con Excel la serie del número de parados.
Evolución de parados
6
5
4
3
2
1
20
08
20 TI
08
20 TII
08
20 TIII
08
TI
20 V
09
20 TI
09
20 TII
09
20 TIII
09
TI
20 V
10
20 TI
10
20 TII
10
20 TIII
10
TI
20 V
11
20 TI
11
20 TII
11
20 TIII
11
T
20 IV
12
20 TI
12
TI
I
0
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
2
Doble Grado en ADE + Derecho – Curso 2014 / 2015
Año/estaciones
1
2
3
4
2008
2009
2010
2011
Parados en millones de habitantes
►EJEMPLO 4.1
Las denuncias en las Oficinas de Información al Consumidor en los últimos años han sido (expresadas
en decenas de miles)
2007
2008
2009
2010
1º cuatrimestre
5
8
10
11,5
2º cuatrimestre
3,5
5
7
10
3º cuatrimestre
7
9
10,5
13
◄
4.2. Componentes de una serie cronológica. Modelos.
Para el estudio de una serie cronológica, ésta se descompone en cuatro componentes:
 Tendencia secular,  (t ) : Es el movimiento de la serie a largo plazo, es decir, refleja el
comportamiento general de la serie. Por ejemplo, la tendencia creciente del IPC.
 Variación estacional, E (t ) : Representa fluctuaciones de la serie en períodos de tiempo que se
repiten con una periodicidad conocida. Por ejemplo, pretende recoger los crecimientos y
disminuciones en la serie por el hecho de estar en una determinada estación del año.
 Variación cíclica, C (t ) : Representa el comportamiento de la serie de carácter periódico, con
períodos de duración diferente, desconocida y en general superior a un año. Por ejemplo, los
ciclos económicos con etapas de prosperidad, recesión y recuperación.
 Variación irregular, residual o aleatoria,  (t ) : Refleja hechos impredecibles que ocurren
aleatoriamente y que normalmente suponen ligeras desviaciones de los valores de la variable
respecto de las componentes anteriores, aunque en otras ocasiones no es así (catástrofes como el
terremoto de Japón, …)
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
3
Doble Grado en ADE + Derecho – Curso 2014 / 2015
El primer problema que se nos plantea es la construcción de un modelo que reuniendo las anteriores
componentes explique el comportamiento de la serie cronológica. Básicamente podemos considerar dos
modelos.
 Modelo aditivo: Supone que las observaciones se generan como suma de las cuatro
componentes
Y (t )   (t )  E(t )  C(t )   (t )
En este modelo cada componente se expresa en la misma unidad que las observaciones.
La variación irregular es independiente de las demás componentes, es decir, la magnitud de sus
valores no depende de las otras componentes.
 Modelo multiplicativo: La observaciones están generadas por el producto de las componentes
(modelo multiplicativo puro)
Y (t )   (t ) E(t )C(t ) (t )
En este modelo la tendencia secular se expresa en la misma unidad que las observaciones y las
demás componentes en tantos por uno. Aquí no se cumple la hipótesis básica de independencia
de la variación irregular respecto de las demás componentes. Una variante de este modelo, el
modelo multiplicativo mixto
Y (t )   (t ) E(t )C(t )   (t )
sí cumple la anterior hipótesis.
En términos generales es más adecuado el modelo multiplicativo que el aditivo para la descripción de
fenómenos económicos (por ejemplo, los factores estacionales y cíclicos no afectarán de la misma
manera, en términos absolutos, a las ventas de un pequeño comercio y de un hipermercado, sino
proporcionalmente al volumen de ventas de cada uno)
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
4
Doble Grado en ADE + Derecho – Curso 2014 / 2015
 Procedimiento para determinar el tipo de modelo
Existen varios procedimientos para determinar el tipo de modelo al que responde una serie cronológica.
La idea en todos consiste en poner de manifiesto si las fluctuaciones de la serie son aproximadamente
constantes o proporcionales al valor de la tendencia. Uno de ellos es:
Análisis de la variabilidad de las diferencias y cocientes estacionales.
Calculamos las diferencias y cocientes estacionales: Para cada estación j se comparan los datos en años
consecutivos, (i-1), i, mediante la diferencia y cociente de ambos.
kij 
dij  yij  yi 1 j
yij
yi 1 j
A continuación calculamos los coeficientes de variación sobre las diferencias y sobre los cocientes. Si
CV (d )  CV (k ) se elegirá el modelo aditivo, en caso contrario se optará por el modelo multiplicativo.
►EJEMPLO 4.2
Estudiemos la conveniencia del modelo aditivo o multiplicativo sobre los datos del ejemplo 4.1.
1º cuatrimestre
5
8
10
11,5
2007
2008
2009
2010
2º cuatrimestre
3,5
5
7
10
3º cuatrimestre
7
9
10,5
13
Solución:
dij  yij  yi 1 j
2007
2008
2009
2010
kij 
yij
yi 1 j
1º cuatrimestre
--8  5=3
2
1,5
2º cuatrimestre
--5  3,5=1,5
2
3
3º cuatrimestre
--9  7=2
1,5
2,5
1º cuatrimestre
2º cuatrimestre
3º cuatrimestre
---
---
---
2007
5
8
9
 1, 6
 1, 29
 1, 43
5
7
3,5
2009
1,25
1,17
1,4
2010
1,15
1,24
1,43
Con los datos de cada tabla calculamos la media, varianza y desviación típica para finalmente hallar el
2008
coeficiente de variación:
d  2,11
Sd2  0,32
Sd  0,57

CV (d ) 
k  1,33
Sk2  0, 02
Sk  0,14

CV (k ) 
Sd
 0, 27
d
Sk
 0,105
k
CV (d )  CV (k ) , por tanto sería más adecuado el modelo multiplicativo.
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
5
Doble Grado en ADE + Derecho – Curso 2014 / 2015
4.3. Tendencia secular: ajuste de una línea recta. Suavizamiento (medias
móviles).
Estudiaremos dos procedimientos para la determinación de la tendencia secular en una serie
cronológica:
 El primer método tiene un enfoque global, consiste en el ajuste de una recta de mínimos
cuadrados al conjunto de todas las observaciones (podría considerarse el ajuste de otra función
si las características de la serie así lo indicaran).
 El segundo método tiene un enfoque local, sólo se utilizan algunas observaciones para el
cálculo de la tendencia en cada período mediante la media de dichas observaciones (medias
móviles).
Es aconsejable utilizar métodos locales en las previsiones a corto plazo porque se adaptan mejor y más
rápidamente a las circunstancias cambiantes. Sin embargo, en las previsiones a largo plazo donde nos
apoyamos en aspectos permanentes de la evolución del fenómeno es mejor usar métodos globales.
Método del ajuste de una recta de mínimos cuadrados (enfoque global).
Considerando una serie cronológica como un caso particular de variable estadística bidimensional,
ajustaremos la recta de regresión de mínimos cuadrados de y/x tal y como hemos visto en el tema 3.
►EJEMPLO 4.3
De nuevo utilizaremos los datos del ejemplo 4.1, para obtener la tendencia secular mediante el ajuste
de una recta por mínimos cuadrados.
Para que los datos sobre los que vamos a obtener la tendencia secular contengan fundamentalmente a
ésta, se eliminan previamente las oscilaciones debidas a factores estacionales calculando los valores
medios anuales. Y sobre dichos valores realizamos el ajuste.
2007
2008
2009
2010
ti
2007
2008
2009
2010
totales
1º cuatrimestre 2º cuatrimestre 3º cuatrimestre media anual
5
3,5
7
5,17
8
5
9
7,33
10
7
10,5
9,17
11,5
10
13
11,50
5  3,5  7
11,5  10  13
y1 
 5,17
...
y4 
 11,5
3
3
xi  ti  2006 yi  media anual
xi yi
xi2
1
5,17
1
5,17
2
7,33
4
14,66
3
9,17
9
27,51
4
11,50
16
46
10
33,17
30
93,34
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
6
Doble Grado en ADE + Derecho – Curso 2014 / 2015
Cuando se trabaja con años, un cambio de origen del tipo xi  ti  2006 facilita notablemente los
cálculos.
Exactamente igual que en el tema 3, obtenemos la recta de regresión de y/x:
Finalmente deshacemos el cambio de origen
xi  ti  2006 y expresamos
y como la tendencia
secular  (t ) a la que representa:
y  3,07  2,088x   (t )  3,07  2,088  t  2006    (t )  4185, 458  2,088t
◄
Método de las medias móviles (Enfoque local).
En este método no se supone una forma funcional para la tendencia, bien sea una recta o cualquier otro
tipo de curva.
El método de las medias móviles es un método de suavizamiento de la serie cronológica que
transforma las observaciones originales (con un representación gráfica típica de dientes de sierra) en
unos valores con menores fluctuaciones. Para la aplicación de este método se van calculando
sucesivamente medias sobre subconjuntos de datos originales, en cada nueva media se elimina la
observación más antigua e introduce la siguiente observación, avanzando así desde la primera hasta la
última de las observaciones (de ahí su calificativo de móviles).
Las anteriores medias móviles utilizan igual ponderación para cada una de las observaciones (medias
móviles no ponderadas), otra posibilidad consiste en considerar ponderaciones distintas, por ejemplo,
con el objeto de darle más importancia a las observaciones centrales en el cálculo de cada media
(medias móviles ponderadas).
Se denomina media móvil de amplitud h a la que se calcula sobre h observaciones.
Cuando este método se utiliza para la obtención de la tendencia secular, en el conjunto de datos sobre
los que se calcula cada media móvil deben estar representadas todas las estaciones eliminando así los
altibajos debidos a factores estacionales (h debe ser igual al número de estaciones o un múltiplo de
éste).
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
7
Doble Grado en ADE + Derecho – Curso 2014 / 2015
El valor de cada media móvil se asocia al período central de los períodos sobre los que se ha calculado.
Si h es impar el período central está clara y unívocamente determinado (ejemplo 4.4), sin embargo,
cuando h es par hay dos períodos centrales y la media móvil se asocia al punto intermedio entre ambos
períodos. Para que las medias móviles siempre estén referidas o los mismos períodos que las
observaciones originales, en este último caso es necesario proceder a centrar las medias móviles para lo
que se volverán a calcular medias móviles de amplitud 2 sobre las medias móviles de amplitud h
(ejemplo 4.5).
►EJEMPLO 4.4
Utilizamos de nuevo los datos del ejemplo 4.1, para obtener la tendencia secular mediante medias
móviles.
2007
2008
2009
2010
1º cuatrimestre
5
8
10
11,5
2º cuatrimestre
3,5
5
7
10
3º cuatrimestre
7
9
10,5
13
Calculando medias móviles de amplitud 3 incluiremos en su obtención una observación de cada
cuatrimestre, compensando (suavizando) así los mayores y menores valores que se presentan en las
distintas estaciones.
5  3,5  7
 5,17
3
3,5  7  8
 6,17
3
medias
1º cuatrimestre
móviles
2007
--2008
6,67
2009
8,67
2010
10,67
7 85
 6, 67
3
2º cuatrimestre
3º cuatrimestre
5,17
7,33
9,17
11,5
6,17
8
9,67
---
...
◄
►EJEMPLO 4.5
Obtenga la tendencia secular mediante medias móviles.
2006
2007
2008
2009
2010
1º trimestre
7
10
13,5
17
18,1
2º trimestre
5
7,1
8,9
11,2
12,7
3º trimestre
2,4
3,6
4,5
5,3
6,6
Calculamos las medias móviles de amplitud 4 que estarán
4º trimestre
1,1
1,4
1,6
2
2,4
asociadas al punto central de los 4
trimestres sobre los que se calcula:
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
8
Doble Grado en ADE + Derecho – Curso 2014 / 2015
media móvil
amplitud 4
1º trimestre
2º trimestre
2006
3º trimestre
4º semestre
1º trimestre
año siguiente
3,875
4,625
5,15
2007
5,45
5,525
6,4
6,85
2008
7,075
7,125
8,0
8,575
2009
8,775
8,875
9,15
9,525
2010
9,85
9,95
donde las medias se han calculado de la siguiente forma:
3,875 
7  5  2, 4  1,1
4
4, 625 
5  2, 4  1,1  10
4
5,15 
2, 4  1,1  10  1, 7
...
4
A continuación procedemos a centrar las medias móviles en los mismos períodos que las
observaciones de la serie, tomando medias móviles de amplitud 2 sobre las anteriores medias móviles
de amplitud 4:
4, 25 
3,875  4, 625
2
4,8875 
medias móviles
amplitud 2
2006
2007
2008
2009
2010
4, 625  5,15
2
5,3 
5,15  5, 45
...
2
1º trimestre
2º trimestre
3º trimestre
4º trimestre
--5,3
6,9625
8,675
9,6875
--5,4875
7,1
8,825
9,9
4,25
5,9625
7,5625
9,0125
---
4,8875
6,625
8,2875
9,3375
--◄
Figura 4.1. Representación gráfica de la Tendencia obtenida por el enfoque global (recta de
regresión) y por el enfoque local (medias móviles) para una serie del número de turistas.
25000
20000
15000
10000
5000
19
95
_
19 3
96
_
19 2
97
_
19 1
97
_
19 4
98
_
19 3
99
_
20 2
00
_
20 1
00
_
20 4
01
_
20 3
02
_
20 2
03
_
20 1
03
_
20 4
04
_
20 3
05
_
20 2
06
_1
0
Serie
Tendencia (Recta de Regresión)
Tendencia (Medias Móviles)
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
9
Doble Grado en ADE + Derecho – Curso 2014 / 2015
4.4. Variación estacional: índices de variación estacional.
En el modelo multiplicativo la componente estacional de una serie cronológica se mide con un índice
adimensional denominado índice de variación estacional, éste se expresa en porcentajes e indica la
fluctuación del valor de la serie en dicha estación respecto del valor medio de la tendencia a lo largo del
año. Por ejemplo, un índice de variación estacional del 90% indica que en esa estación hay una
disminución del 10% en relación al valor medio de la tendencia.
En el modelo aditivo la componente estacional indica en términos absolutos (expresada en las mismas
unidades que la variable observada) la cantidad en que se ha superado, si es positiva, o no se ha
alcanzado, si es negativa, la tendencia media a lo largo del año. Por ejemplo, un valor de la componente
estacional de -150€ indica que a esa estación le corresponde un valor 150€ por debajo del valor medio
de la tendencia.
En ocasiones interesa conocer las variaciones estacionales y eliminarlas de las observaciones de la serie
para poder ver mejor el comportamiento de ésta ajeno a causas estacionales. La eliminación de la
componente estacional se conoce como desestacionalización de la serie y permite entre otras cosas
comparar valores observados en estaciones distintas que están influidos, con toda seguridad, por este
hecho. Así, si las ventas de juguetes presentan una variación estacional según un modelo multiplicativo
del 48% en el mes de marzo y del 156% en el mes de diciembre no podremos comparar directamente
las ventas de 13500€ y 41500€ respectivamente en los meses de marzo y diciembre del año pasado.
Suponiendo el modelo multiplicativo, como se ha indicado, y eliminando el efecto estacional mediante
cociente (mediante diferencia si el modelo es aditivo), obtendríamos el valor de la serie si ésta no se
hubiera visto afectada por factores estacionales
Y (t )   (t ) E (t )C (t ) (t ) 
marzo :
13500
 28125
0, 48
Y (t )
  (t )C (t ) (t )
E (t )
diciembre :
41500
 26602,56
1,56
Donde se observa que el mes de marzo tuvo relativamente un mejor comportamiento que diciembre en
cuanto a las ventas (aunque en términos absolutos éstas fueron claramente inferiores, 13500<41500).
Vamos a estudiar tres procedimientos para la obtención de la variación estacional.
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
10
Doble Grado en ADE + Derecho – Curso 2014 / 2015
Método de las medias simples.
Denominado también método de las relaciones de las medias estacionales respecto a la tendencia.
►EJEMPLO 4.6
Explicamos el método con los datos del ejemplo 4.1.
2007
2008
2009
2010
1.
1º cuatrimestre
5
8
10
11,5
2º cuatrimestre
3,5
5
7
10
3º cuatrimestre
7
9
10,5
13
media anual
5,17
7,33
9,17
11,50
Sobre los valores medios anuales ajustamos la recta de regresión de mínimos cuadrados como
se hizo en el ejemplo 4.3.
y  3,07  2,088x   (t )  3,07  2,088  t  2006    (t )  4185, 458  2,088t
La pendiente b de la recta estima lo que varia la tendencia por unidad de tiempo (un año en nuestro
caso), por tanto la tendencia variará
En este ejemplo la tendencia crece
2.
b
por cada estación que transcurra (s=número de estaciones).
s
2, 088
 0, 696 cada cuatrimestre.
3
Calculamos los valores medios en cada estación
5  8  10  11,5
 8, 625
4
1º cuatrimestre
5
8
10
11,5
...
2º cuatrimestre
3,5
5
7
10
7  9  10,5  13
 9,875
4
3º cuatrimestre
7
9
10,5
13
2007
2008
2009
2010
medias por
8,625
6,375
9,875
estación ( y i )
medias
8,625
5,679
8,483
corregidas ( ei )
Seguidamente eliminamos la tendencia de los anteriores valores medios por estación, restando
tantas veces
b 2, 088

 0, 696 como estaciones del año han pasado, obteniendo las medias
s
3
b

corregidas  ei  yi  (i  1)   :
s

TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
11
3.
Doble Grado en ADE + Derecho – Curso 2014 / 2015
Calculamos la media de las medias corregidas, conocida como media global corregida
1 s 

 M   ei  :
s i 1 

4.
En el modelo multiplicativo la variación estacional se expresa mediante los índices de variación
estacional (IVE). Calculamos los IVE se obtienen del siguiente modo
E1 
e
e1
e
 100, E 2  2  100, , E s  s  100
M
M
M
Comparando las medias corregidas con su promedio (por cociente o diferencia según el modelo sea
multiplicativo o aditivo) obtenemos la variación estacional.
Media global
corregida
I.V.E.
media
8,625
corregida
modelo
113,55%
multiplicativo
modelo
1,0293
aditivo
8, 625
100  113,55
7,5957
8,625  7,5957  1,0293
5,679
8,483
74,77%
111,68%
-1,9167
0,8873
...
8, 483
100  111, 68
7,5957
...
8, 483  7,5957  0,8873
7,5957
Los IVE son valores adimensionales con la propiedad de que su media es 100 (1 si los IVE están
expresados en tantos por uno). En el primer cuatrimestre el número de denuncias es un 13,55%
mayor que la tendencia media anual para un cuatrimestre, en el segundo cuatrimestre las denuncias
no llegan a ser el 100% de la tendencia media anual para un cuatrimestre sino que es un 25,33%
menor (100-74,77=25,23), …
En el modelo aditivo la variación estacional está expresada en las mismas unidades que la variable
observada (decenas de miles de denuncias en este ejemplo) y su media es cero
( 1,0293 1.9167  0,8873  0,0001  0 debido a pequeños errores de redondeo). En el primer
cuatrimestre hay 1,0293 decenas de miles de denuncias más que la tendencia media anual para un
cuatrimestre (10293 denuncias más), en el segundo cuatrimestre hay 19167 denuncias menos que
la tendencia media anual para un cuatrimestre, …
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
◄
12
Doble Grado en ADE + Derecho – Curso 2014 / 2015
►EJEMPLO 4.7
Con el método de las medias simples obtenga la variación estacional de los datos del ejemplo 4.5
1.
En primer lugar ajustamos la recta de tendencia sobre las medias anuales:
ti
xi  ti  2005
2006
2007
2008
2009
2010
totales
1
2
3
4
5
15
n5
yi  media anual
xi2
1
4
9
16
25
55
35,35
y
 7, 07
5
3,875
5,525
7,125
8,875
9,950
35,35
15
x 3
5
xi yi
3,875
11,05
21,375
35,5
49,75
121,55
deshacemos el cambio de origen xi  ti  2005 y expresamos y como la tendencia secular  (t ) :
y  2, 42  1,55 x   (t )  2, 42  1,55  t  2005    (t)  3105,33 1,55t
2.
Seguidamente eliminamos la tendencia de los valores medios por estación, restando tantas
veces
b 1,55

 0,3875 como estaciones del año han pasado, obteniendo las medias corregidas:
s
4
 b
13,12   0    13,12
s

3.
 b
1, 7   3    0,5375
 s
...
Calculamos la media de las medias corregidas (media global corregida):
6, 48875 
13,12  8,5925  3, 705  0,5375
4
Comparando las medias corregidas con su promedio (por cociente o diferencia según el modelo sea
multiplicativo o aditivo) obtenemos la variación estacional.
13,12
100  202,196
6, 48875
...
0,5375
100  8, 284
6, 48875
13,12  6, 48875  6,631
...
0,5375  6, 48875  5,951
En la siguiente tabla se recogen todos los cálculos:
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
13
2006
2007
2008
2009
2010
media por
estación ( y i )
media
corregida ( ei )
modelo
multiplicativo
(IVE)
modelo
aditivo
Doble Grado en ADE + Derecho – Curso 2014 / 2015
1º trimestre
2º trimestre
3º trimestre
4º trimestre
7
5
2,4
1,1
10
7,1
3,6
1,4
13,5
8,9
4,5
1,6
17
11,2
5,3
2
18,1
12,7
6,6
2,4
13,12
8,98
4,48
1,7
media anual
3,875
5,525
7,125
8,875
9,950
media global
corregida
13,12
8,5925
3,705
0,5375
M=6,48875
202,196%
132,421%
57,099%
8,284%
6,631
2,104
 2,784
 5,951
◄
En los dos métodos siguientes la idea básica es eliminar de las observaciones el valor de la tendencia
secular, para ello es fundamental conocer el modelo que se adapta a la serie cronológica.
En el modelo multiplicativo eliminaremos la tendencia mediante cociente de las observaciones sobre la
tendencia
Y (t )   (t ) E (t )C (t ) (t ) 
Y (t )
 E (t )C (t ) (t )
 (t )
Mientras que en el modelo aditivo lo haremos por diferencia
Y (t )   (t )  E(t )  C(t )   (t )  Y (t )  (t )  E(t )  C(t )   (t )
Posteriormente se promedian estos valores ( E (t )C (t ) (t ) ó E(t )  C (t )   (t ) ) sobre cada una de las
estaciones, de esta forma los efectos unas veces positivos, otras negativos, de las componentes C (t ) y
 (t ) se anulan, recogiéndose en dicho promedio fundamentalmente el valor de la componente
estacional.
Método de la razón (o diferencia) a la tendencia.
Explicamos el método con los mismos datos del ejemplo 4.1 en el siguiente ejemplo.
►EJEMPLO 4.8
2007
2008
2009
2010
1º cuatrimestre
5
8
10
11,5
2º cuatrimestre
3,5
5
7
10
3º cuatrimestre
7
9
10,5
13
media anual
5,17
7,33
9,17
11,50
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
14
Doble Grado en ADE + Derecho – Curso 2014 / 2015
1.
Sobre los valores medios anuales ajustamos la recta de regresión de mínimos cuadrados como
se hizo en el ejemplo 4.3.
y  3,07  2,088x   (t )  3,07  2,088  t  2006    (t )  4185, 458  2,088t
2.
Estimamos la tendencia secular para cada una de las estaciones de cada año, teniendo presente
que la tendencia  (t )  4185, 458  2,088t para un año t se asigna al período central del año (2º
cuatrimestre en este ejemplo) y que la tendencia varía
b 2,088

 0,696 cada estación que pasa.
s
3
 (2007)  4185, 458   2,088  2007   5,158  2º cuatrimestre de 2007
…
 (2010)  4185, 458   2,088  2010  11, 422  2º cuatrimestre de 2010
En el 3º cuatrimestre de 2007 la tendencia será
b 2, 088

 0, 696 más que en el 2º cuatrimestre:
s
3
5,158+0,696=5,854
En el 1º cuatrimestre de 2007 la tendencia será
b 2, 088

 0, 696 menos que en el 2º
s
3
5,158  0,696=4,462
cuatrimestre:
…
Análogamente en el resto de los años.
3.
Se elimina de las observaciones, Y(t), el valor de la tendencia,  (t ) , realizando los cocientes
Y (t )
si suponemos el modelo multiplicativo y mediante las diferencias Y (t )   (t ) si el modelo es
 (t )
aditivo.
En lo que sigue supondremos el modelo multiplicativo (más adelante se repetirá todo para el
modelo aditivo).
5
 1,121
4, 462
4.
13
 1, 073
12,118
Calculamos la media por estación de los anteriores valores y la media (M) de dichas medias (que es
igual a la media global de todos los cocientes
5.
...
Y (t )
).
 (t )
Los índices de variación estacional (I.V.E.) se obtienen como en el método anterior, es decir, como
el cociente de las medias por estación sobre la media global (el resultado se multiplica por 100 para
expresarlo en tantos por ciento)
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
15
Doble Grado en ADE + Derecho – Curso 2014 / 2015
1,121  1, 221  1,158  1, 072
1,196  1,133  1, 047  1, 073
 1,143
...
 1,11225
4
4
1,143  0, 74875  1,11225
 1, 001333
3
1,143
100  114,148%
1, 001333
1,11225
100  111, 077%
1, 001333
...
En la siguiente tabla se recogen todos los cálculos (modelo multiplicativo):
Y (t )
2007
2008
2009
2010
 (t )
2007
2008
2009
2010
Y (t )
 (t )
2007
2008
2009
2010
media por
estación
I.V.E.
1º cuatrimestre
5
8
10
11,5
1º cuatrimestre
4,462
6,550
8,638
10,726
2º cuatrimestre
3,5
5
7
10
2º cuatrimestre
5,158
7,246
9,334
11,422
3º cuatrimestre
7
9
10,5
13
3º cuatrimestre
5,854
7,942
10,030
12,118
1º cuatrimestre
2º cuatrimestre
3º cuatrimestre
1,121
1,221
1,158
1,072
0,679
0,690
0,750
0,876
1,196
1,133
1,047
1,073
media global
1,143
0,74875
1,11225
1,001333
114,148%
74,775%
111,077%
Repetimos los pasos 3 y 4 suponiendo el modelo aditivo
3.
Se elimina de las observaciones, Y(t), el valor de la tendencia,  (t ) , realizando las diferencias
Y (t )   (t ) .
5  4, 462  0,538
4.
13 12,118  0,882
...
Calculamos la media por estación de los anteriores valores y la media de dichas medias (que es
igual a la media global de todas las diferencias Y (t )   (t ) ). La variación estacional (V.E.) se
obtiene como diferencia de la media por estación menos la media global
0,538  1, 450  1,362  0, 774
 1, 031
4
...
1,146  1, 058  0, 470  0,882
 0,889
4
1, 031  1,915  0,889
 0, 00167
3
1,031  0,00167  1,02933
...
0,889  0,00167  0,88733
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
16
Doble Grado en ADE + Derecho – Curso 2014 / 2015
En la siguiente tabla se recogen todos los cálculos (modelo aditivo):
Y (t )
2007
2008
2009
2010
 (t )
2007
2008
2009
2010
Y (t )   (t )
2007
2008
2009
2010
media por
estación
V.E.
1º cuatrimestre
5
8
10
11,5
1º cuatrimestre
4,462
6,550
8,638
10,726
1º cuatrimestre
0,538
1,450
1,362
0,774
2º cuatrimestre
3,5
5
7
10
2º cuatrimestre
5,158
7,246
9,334
11,422
2º cuatrimestre
−1,658
−2,246
−2,334
−1,422
3º cuatrimestre
7
9
10,5
13
3º cuatrimestre
5,854
7,942
10,030
12,118
3º cuatrimestre
1,146
1,058
0,470
0,882
media global
1,031
−1,915
0,889
0,00167
1,02933
−1,91667
0,88733
◄
Repetimos este método tanto para el modelo multiplicativo como aditivo en un ejemplo con un número
par de estaciones. La única diferencia con el ejemplo anterior está en la etapa 2 donde el valor de la
tendencia en un año t estará asignada al punto medio del año, es decir, entre las dos estaciones
centrales. Para referir los valores de la tendencia a los mismos períodos que las observaciones habrá
que centrar las estimaciones de la tendencia en dichos períodos como se expone en el siguiente
ejemplo.
►EJEMPLO 4.9.
Utilizamos los datos del ejemplo 4.5.
1.
Sobre los valores medios anuales ajustamos la recta de regresión de mínimos cuadrados como se
hizo en el ejemplo 4.7
y  2, 42  1,55 x   (t )  2, 42  1,55  t  2005    (t)  3105,33 1,55t
2.
Estimamos la tendencia secular para cada una de las estaciones de cada año, teniendo presente que
la tendencia  (t )  3105,33  1,55t para un año t se asigna al punto central del año (punto entre el
2º y 3º trimestres en este ejemplo), que la tendencia varía
b 1,55

 0,3875 cada estación que
s
4
 0,3875

pasa y la mitad 
 0,19375  si sólo ha transcurrido media estación. Así:
 2

 (2006)   (t )  3105,33  1,55  2006   3,97  punto entre 2º y 3º trimestres de 2006
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
17
Doble Grado en ADE + Derecho – Curso 2014 / 2015
…
 (2010)   (t )  3105,33  1,55  2010   10,17  punto entre 2º y 3º trimestres de 2010
La tendencia centrada en el 3º trimestre de 2006 será:
3,97+0,19375=4,16375
…
La tendencia centrada en el 3º trimestre de 2010 será:
En el 4º trimestre de 2006 la tendencia será
10,17+0,19375=10,36375
b 1,55

 0,3875 más que en el 3º trimestre:
s
4
4,16375+0,3875=4,55125
En el 2º trimestre de 2006 la tendencia será
b 1,55

 0,3875 menos que en el 3º trimestre:
s
4
4,16375−0,3875=3,77625
Y en el 1º trimestre de 2006 la tendencia será
b 1,55

 0,3875 menos que en el 2º trimestre:
s
4
3,77625−0,3875=3,38875
Análogamente en el resto de los años.
Las etapas 3 y 4 son idénticas a las del ejemplo anterior.
En la siguiente tabla se recogen todos los cálculos (modelo multiplicativo):
Y (t )
2006
2007
2008
2009
2010
 (t )
2006
2007
2008
2009
2010
Y (t )
 (t )
2006
2007
2008
2009
2010
media por
estación
I.V.E.
1º trimestre
7
10
13,5
17
18,1
1º trimestre
3,38875
4,93875
6,48875
8,03875
9,58875
2º trimestre
5
7,1
8,9
11,2
12,7
2º trimestre
3,77625
5,32625
6,87625
8,42625
9,97625
3º trimestre
2,4
3,6
4,5
5,3
6,6
3º trimestre
4,16375
5,71375
7,26375
8,81375
10,36375
4º trimestre
1,1
1,4
1,6
2
2,4
4º trimestre
4,55125
6,10125
7,65125
9,20125
10,75125
1º trimestre
2º trimestre
3º trimestre
4º trimestre
2,06566
2,02480
2,08052
2,11476
1,88763
1,32406
1,33302
1,29431
1,32918
1,27302
0,57640
0,63006
0,61951
0,60133
0,63684
0,24169
0,22946
0,20912
0,21736
0,22323
media global
2,03467
1,31072
0,61283
0,22417
1,0456
194,59%
125,36%
58,61%
21,44%
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
media anual
3,875
5,525
7,125
8,875
9,950
18
Doble Grado en ADE + Derecho – Curso 2014 / 2015
En la siguiente tabla se recogen todos los cálculos (modelo aditivo):
Y (t )
2006
2007
2008
2009
2010
 (t )
2006
2007
2008
2009
2010
Y (t )   (t )
2006
2007
2008
2009
2010
media por
estación
V.E.
1º trimestre
7
10
13,5
17
18,1
1º trimestre
3,38875
4,93875
6,48875
8,03875
9,58875
1º trimestre
3,61125
5,06125
7,01125
8,96125
8,51125
2º trimestre
5
7,1
8,9
11,2
12,7
2º trimestre
3,77625
5,32625
6,87625
8,42625
9,97625
2º trimestre
1,22375
1,77375
2,02375
2,77375
2,72375
3º trimestre
2,4
3,6
4,5
5,3
6,6
3º trimestre
4,16375
5,71375
7,26375
8,81375
10,36375
3º trimestre
−1,76375
−2,11375
−2,76375
−3,51375
−3,76375
4º trimestre
1,1
1,4
1,6
2
2,4
4º trimestre
4,55125
6,10125
7,65125
9,20125
10,75125
4º trimestre
−3,45125
−4,70125
−6,05125
−7,20125
−8,35125
media anual
3,875
5,525
7,125
8,875
9,950
media global
6,63125
2,10375
−2,78375
−5,95125
0
6,63125
2,10375
−2,78375
−5,95125
◄
NOTA: El método de las medias simples (modelo aditivo) y el método de la diferencia a la tendencia
coinciden. Las pequeñas diferencias que se aprecian en nuestros ejemplos son debidas a errores de
redondeo.
Método de la razón (o diferencia) a las medias móviles.
Este método es igual que el anterior con la única diferencia de que aquí se estima la tendencia para cada
período (estación) mediante la técnica de suavizamiento de las medias móviles tal y como vimos en los
ejemplos 4.4 y 4.5, según el número de estaciones sea impar o par.
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
19
Doble Grado en ADE + Derecho – Curso 2014 / 2015
►EJEMPLO 4.10.
Utilizamos los datos del ejemplo 4.4 donde ya se calcularon las medias móviles para estimar la
tendencia en cada estación.
Modelo multiplicativo:
Y (t )
2007
2008
2009
2010
 (t )
2007
2008
2009
2010
Y (t )
 (t )
2007
2008
2009
2010
media por
estación
I.V.E.
1º cuatrimestre
5
8
10
11,5
1º cuatrimestre
--6,67
8,67
10,67
2º cuatrimestre
3,5
5
7
10
2º cuatrimestre
5,17
7,33
9,17
11,5
3º cuatrimestre
7
9
10,5
13
3º cuatrimestre
6,17
8
9,67
---
1º cuatrimestre
2º cuatrimestre
3º cuatrimestre
--1,19940
1,15340
1,07779
0,67698
0,68213
0,76336
0,86957
1,13452
1,12500
1,08583
---
media global
1,14353
0,74801
1,11512
1,00222
114,10%
74,64%
111,26%
1º cuatrimestre
5
8
10
11,5
1º cuatrimestre
--6,67
8,67
10,67
1º cuatrimestre
--1,33
1,33
0,83
2º cuatrimestre
3,5
5
7
10
2º cuatrimestre
5,17
7,33
9,17
11,5
2º cuatrimestre
−1,67
−2,33
−2,17
−1,5
3º cuatrimestre
7
9
10,5
13
3º cuatrimestre
6,17
8
9,67
--3º cuatrimestre
0,83
1
0,83
---
media global
1,16333
−1,91750
0,88667
0,04417
1,11917
−1,96167
0,84250
Modelo aditivo:
Y (t )
2007
2008
2009
2010
 (t )
2007
2008
2009
2010
Y (t )   (t )
2007
2008
2009
2010
media por
estación
V.E.
◄
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
20
Doble Grado en ADE + Derecho – Curso 2014 / 2015
►EJEMPLO 4.11.
Usamos los datos del ejemplo 4.5 donde se calcularon las medias móviles centradas en cada estación.
Modelo multiplicativo:
1º trimestre
Y (t )
2006
7
2007
10
2008
13,5
2009
17
2010
18,1
1º
trimestre
 (t )
2006
--2007
5,3
2008
6,9625
2009
8,675
2010
9,6875
Y (t )
1º trimestre
 (t )
2006
--2007
1,88679
2008
1,93896
2009
1,95965
2010
1,86839
media por
1,91345
estación
I.V.E.
191,96%
Modelo aditivo:
1º trimestre
Y (t )
2006
7
2007
10
2008
13,5
2009
17
2010
18,1
1º trimestre
 (t )
2006
--2007
5,3
2008
6,9625
2009
8,675
2010
9,6875
Y (t )   (t )
1º trimestre
2006
--2007
4,7
2008
6,5375
2009
8,325
2010
8,4125
media por
6,99375
estación
V.E.
6,83516
2º trimestre
5
7,1
8,9
11,2
12,7
2º trimestre
--5,4875
7,1
8,825
9,9
3º trimestre
2,4
3,6
4,5
5,3
6,6
3º trimestre
4,25
5,9625
7,5625
9,0125
---
4º trimestre
1,1
1,4
1,6
2
2,4
4º trimestre
4,8875
6,625
8,2875
9,3375
---
2º trimestre
3º trimestre
4º trimestre
--1,29385
1,25352
1,26912
1,28283
0,56471
0,60377
0,59504
0,58807
---
0,22506
0,21132
0,19306
0,21419
---
media global
1,27483
0,58790
0,21091
0,99677
127,90%
58,98%
21,16%
2º trimestre
5
7,1
8,9
11,2
12,7
2º trimestre
--5,4875
7,1
8,825
9,9
2º trimestre
--1,6125
1,8
2,375
2,8
3º trimestre
2,4
3,6
4,5
5,3
6,6
3º trimestre
4,25
5,9625
7,5625
9,0125
--3º trimestre
−1,85
−2,3625
−3,0625
−3,7125
---
4º trimestre
1,1
1,4
1,6
2
2,4
4º trimestre
4,8875
6,625
8,2875
9,3375
--4º trimestre
−3,7875
−5,225
−6,6875
−7,3375
---
media global
2,14688
−2,74688
−5,75938
0,15859
1,98828
−2,90547
−5,91797
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
21
Doble Grado en ADE + Derecho – Curso 2014 / 2015
◄
4.5. Predicción
Conociendo las cuatro componentes de una serie cronológica así como el modelo según el cual se
relacionan podríamos conocer el valor de la serie en cualquier período. La variación irregular es por
naturaleza desconocida, del resto de componentes podemos tener a lo sumo una estimación de las
mismas y el modelo es sencillamente un esquema artificial impuesto para facilitar el estudio de la serie.
Por tanto, no se podrá conocer el valor de la serie para un período futuro, lo más que se podrá hacer es
una predicción lo mejor posible.
En este curso no hemos entrado en el estudio de la variación cíclica por lo que la predicción se hará en
base a la tendencia secular y variación estacional.
Si el modelo es aditivo, Y (t )   (t )  E(t )  C(t )   (t ) , la estimación del valor de la serie, Y (t ) , para un
período futuro t estará dada por:
Y (t )   (t )  E (t ) .
Si la serie sigue un modelo multiplicativo, Y (t )   (t ) E(t )C(t ) (t ) , la predicción de su valor para un
período futuro se hará mediante:
Y (t )   (t ) E (t ) .
En ambos casos se está suponiendo que la variación cíclica no tiene una influencia fuerte en los valores
de la serie.
►EJEMPLO 4.11.
¿Cuál sería el valor de la serie del ejemplo 4.1 en el primer cuatrimestre de 2012?. Utilice los diferentes
métodos y modelos.
Solución:
Según la recta de tendencia ajustada,  (t )  4185, 458  2,088t , el comportamiento medio de la serie
en los cuatrimestres de 2012 es:
 (2012)  4185, 458   2,088  2012   15,598
El valor de la serie para el primer cuatrimestre de 2012 diferirá de este valor medio según la variación
estacional para dicho cuatrimestre:
Método de las media simples
Modelo aditivo
Método de la diferencia a la tendencia
Y (t )   (t )  E (t )  15,598  1,0293  16,6273
Y (t )   (t )  E (t )  15,598  1,02933  16,62733
Como se indicó anteriormente en una nota, estos dos métodos coinciden sobre el modelo aditivo, la
diferencia que se observa es debida a errores de redondeo.
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
22
Doble Grado en ADE + Derecho – Curso 2014 / 2015
Modelo multiplicativo
Método de las media simples
Método de la razón a la tendencia
113,55
114,148
Y (t )   (t ) E (t )  15,598 
 17, 7115
Y (t )   (t ) E (t )  15,598 
 17,8048
100
100
En el método de la razón (diferencia) a las medias móviles la tendencia no se estima mediante el ajuste
de una recta por mínimos cuadrados sobre las medias anuales sino mediante medias móviles, por lo que
tendríamos que calcular el valor de la tendencia a partir de ellas. Haría falta ajustar una recta a las
medias móviles, esta recta no suele diferir mucho de la anterior recta de mínimos cuadrados sobre las
medias anuales. Por este motivo en la práctica también para este último método se procede como en los
dos anteriores: hallamos el valor estimado medio de la tendencia para las estaciones del año utilizando
la recta de mínimos cuadrados sobre las media anuales y posteriormente se modifica de acuerdo al
modelo y a la variación estacional estimada con el método de la razón (diferencia) a las medias
móviles.
Método de la razón a las medias móviles
114,10
Y (t )   (t ) E (t )  15,598 
 17, 7973
100
Método de la diferencia a las medias móviles
Y (t )   (t )  E (t )  15,598  1,11917  16,7172
◄
¿Cuál sería el valor de la serie del ejemplo 4.1 para todos los cuatrimestres de 2012? Utilice el método
de las medias simples y el modelo multiplicativo.
Cuatrimestre
Predicción por el método de las media simples y modelo multiplicativo
1
2
3
Preguntas de teoría del Tema 4
1. Componentes de una serie cronológica. Modelos.
2. Explique los procedimientos para determinar la tendencia secular de una serie
cronológica.
3. Índices de variación estacional. Desestacionalización.
TÉCNICAS CUANTITATIVAS 1 – Doble Grado ADE + Derecho. GRUPO B – TEMA 4
23