4GUIA-complejos en forma polar

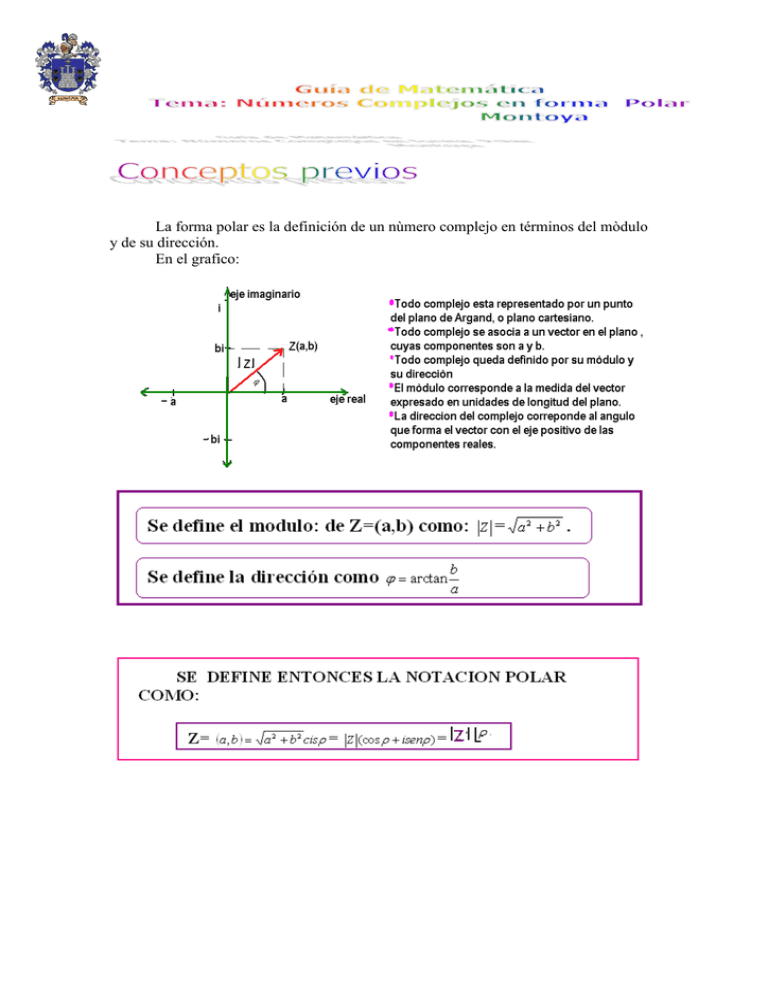
La forma polar es la definición de un nùmero complejo en términos del mòdulo
y de su dirección.
En el grafico:
EJERCICIOS DE APLICACIÓN.
1.- Dados los complejos Z 1 ( 3 ,1)
Z 2 (0,-4)
Exprese cada uno de ellos en forma polar.
Z 3 =2+3i
1
2 ! 135°
2
Exprese cada uno de ellos en forma canónica y binomial.
2.-Dados los complejos: Z 1 =2 3 ! π / 3
3.-Dados los complejos: Z 1 = ( 3 ,-1)
Z 4 =2+i
4.-Calcule en forma polar:
4.1.- Z 1 *Z 2
4.4.-
Z1 * Z 2
Z4
Z2 =
Z 2 = (0,-4)
4.2.- (Z 2 : Z 3 ) 3
4.5.-(Z 2 ) 3 *(Z 3 ) 4
5.- dados los complejos:
Z 2 = (-4,0)
Z 3 = (i, i)
Z 1 = (1, 3 )
Exprese cada uno de ellos en forma polar.
Z3=
1
2
Z3=
2 ! 135°
4.3.- (Z 4 ) −2
Z 4*( Z )3 −2
1
4.6.- (
)
Z3
1
! -60°
3
6.- Dados los complejos: Z 1 =2 2 CIS
π
4
Z2 =
1
2
3 CIS π , exprese cada uno
2
3
de ellos en forma canónica y binomial.
7.- dados los complejos: Z 1 = (-1, 3 )
Z 3 = 2 CIS135°
Z 2 = (0,-4)
Z 4 = 2 CIS -45°
Calcule en forma polar:
7.1.- Z 2 *Z 3
Z
7.2.-  1
 Z4



3
 Z13 * Z 3
7.3.-  4
Z :Z
2
 4
8.- calcule las raíces que se indican:
8.1.- quintas de la unidad real.
8.2.- cuartas de 16i
8.3.-quintas de 32i
8.4.- cuartas de 81
8.5.- cuartas de -16
8.- Considere los complejos representados en los gráficos:
Para cada uno de ellos
8.1.- Escríbalos en forma polar
8.2.- Escríbalos en forma canónica.
8.3 Escríbalos en forma binomial.




2
9.-Considere los complejos de grafico. Determine:
9.1.- Cada uno de ellos escrito en forma polar.
9.2.- El producto de los complejos en forma polar.
9.3.- La cuarta potencia del cuociente entre Z y Z’ en forma polar.
10.-Considere los complejos de grafico. Determine:
10.1.- Cada uno de ellos escrito en forma polar.
10.2.- El producto de los complejos en forma polar.
10.3.- La cuarta potencia del cuociente entre Z y Z’ en forma polar.
10.4.-La raíz sexta del producto de los complejos.
10.5.- La raíz cuarta del complejo Z.
10.6.- la sexta potencia de Z’.
10.7.- Una traslación según el vector v(2,-1) a la suma de los complejos del grafico.