parábola - División de Ciencias Básicas

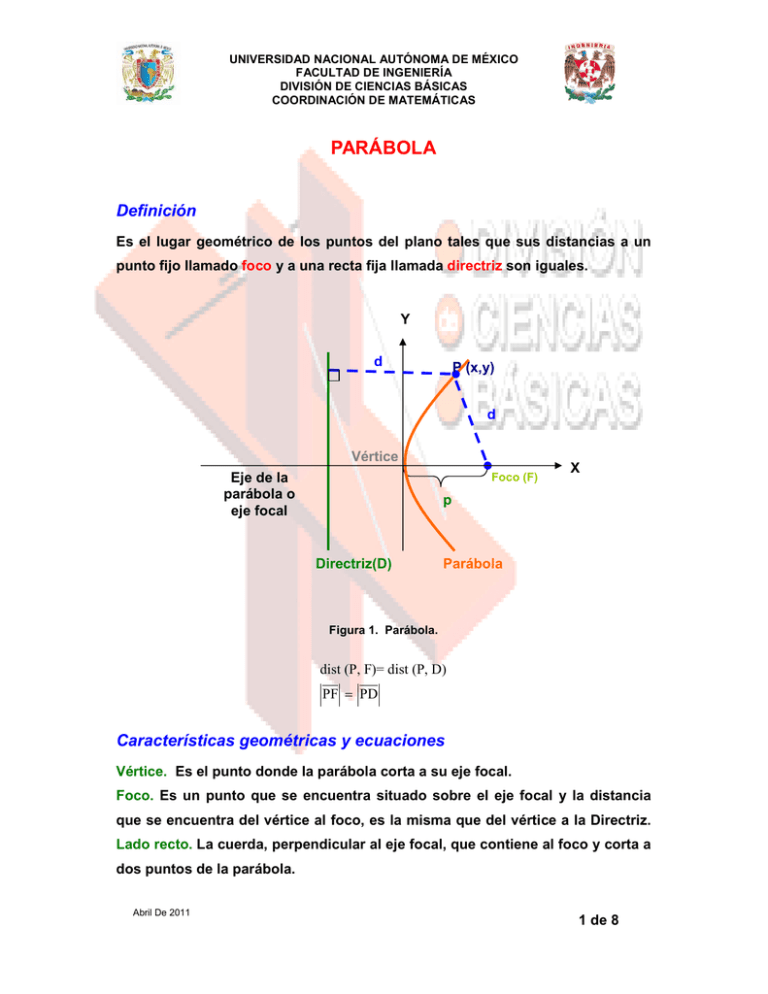
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE MATEMÁTICAS
PARÁBOLA
Definición
Es el lugar geométrico de los puntos del plano tales que sus distancias a un
punto fijo llamado foco y a una recta fija llamada directriz son iguales.
Y
d
P (x,y)
d
Vértice
Eje de la
parábola o
eje focal
Foco (F)
X
p
Directriz(D)
Parábola
Figura 1. Parábola.
dist (P, F)= dist (P, D)
PF = PD
Características geométricas y ecuaciones
Vértice. Es el punto donde la parábola corta a su eje focal.
Foco. Es un punto que se encuentra situado sobre el eje focal y la distancia
que se encuentra del vértice al foco, es la misma que del vértice a la Directriz.
Lado recto. La cuerda, perpendicular al eje focal, que contiene al foco y corta a
dos puntos de la parábola.
Abril De 2011
1 de 8
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE MATEMÁTICAS
Directriz. Línea recta donde la dist (P, F)= dist (P, D); PF = PD . Ver figura 1.
Eje focal. Recta que contiene el foco y es perpendicular a la directriz.
Parámetro p. Distancia del foco al vértice.
La ecuación de la parábola con vértice en el origen y eje focal sobre el eje X
que abre hacia la derecha es:
Y
D
P
Ecuación
y2 = 4px
0
x = -p
X
F(p,0)
Directriz
x= -p
Parábola
Figura 2. Parábola con vértice en el origen y eje focal sobre el eje X que abre hacia la derecha.
Abril De 2011
2 de 8
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE MATEMÁTICAS
La ecuación de la parábola con vértice en el origen y eje focal sobre el eje X
que abre hacia la izquierda es:
Y
P
D
Ecuación
y2 = –4px
Directriz
x= p
X
0
F(-p,0)
x=p
Parábola
Figura 3. Parábola con vértice en el origen y eje focal sobre el eje X que abre hacia la izquierda.
La ecuación de la parábola con vértice en el origen y eje focal sobre el eje Y
que abre hacia abajo es:
Y
Ecuación
D
y=p
0
X
Parábola
P
F(0,-p)
x2 = –4py
Directriz
y= p
Figura 4. Parábola con vértice en el origen y eje focal sobre el eje Y que abre hacia abajo
La ecuación de la parábola con vértice en el origen y eje focal sobre el eje Y
que abre hacia arriba es:
Abril De 2011
3 de 8
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE MATEMÁTICAS
Y
Ecuación
Parábola
x2 = 4py
F(0,p)
P
Directriz
0
y = -p
y= -p
Figura 5. Parábola con vértice en el origen y eje focal sobre el eje Y que abre hacia arriba
Ejemplo:
Obtener la ecuación, el foco y la directriz de la parábola con vértice en el
origen y contiene al punto B(3,4), además su eje focal es paralelo al eje X.
Resolución: Sustituyendo las coordenadas del punto B en la ecuación
y 2 = 4px :
16 = 4p(3)
16 4
p= =
12 3
16
y2 =
x
3
4
4 
Foco: F  , 0  ; Directriz: x=3
3 
Abril De 2011
4 de 8
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE MATEMÁTICAS
Ecuación de una parábola con eje focal paralelo o coincidente con
el eje “X”
A continuación se muestra la representación gráfica de parábolas con eje
paralelo al eje X y vértice en V(h,k)
Y
D
P
Ecuación
(y - k)2 = 4p(x-h)
Directriz
V(h,k)
F(h+p,k)
x= h - p
X
0
Parábola
Figura 6. Parábola con vértice en (h, k) y eje focal paralelo al eje X.
Y
P
D
Ecuación
(y – k)2 = –4p(x - h)
Directriz
F(h-p,k)
Parábola
V(h,k)
x= h - p
x = h+p
0
X
Figura 7. Parábola con vértice en (h, k) y eje focal paralelo al eje X.
Abril De 2011
5 de 8
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE MATEMÁTICAS
Ecuación de una parábola con eje focal paralelo o coincidente con
el eje “Y”.
A continuación se muestra la representación gráfica de parábolas con eje
paralelo al eje Y y vértice en V(h,k)
Y
Ecuación
Parábola
(x - h)2 = 4p(y - k)
F(h,p+k)
P
Directriz
y= k - p
V(h,k)
D
y = k-p
X
0
Figura 8. Parábola con vértice en (h, k) y eje focal paralelo al eje Y con p > 0.
Abril De 2011
6 de 8
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE MATEMÁTICAS
Y
Ecuación
(x - h)2 = –4p(y - k)
y = k+p
D
Directriz
V(h,k)
Parábola
0
y= k - p
P
F(h, k-p)
X
Figura 9. Parábola con vértice en (h, k) y eje focal paralelo al eje Y con p < 0.
Ejemplo:
Determinar las coordenadas del Vértice, Foco y calcular el lado recto de la
parábola de ecuación y 2 − y + 4 x + 5 = 0
Resolución:
Completando el trinomio al cuadrado perfecto
y2 − y +
1
+ 4x + 5 = 0
4
factorizando al trinomio al cuadrado perfecto y 2 − y +
1
se obtiene
4
2
1
1

 y −  = − 4x − 5 +
2
4

simplificando y factorizando el miembro derecho de la ecuación
2
1
19

 y −  = − 4x −
2
4

2
1
19 


 y −  = − 4 x +

2
16 


Abril De 2011
7 de 8
UNIVERSIDAD NACIONAL AUTÓNOMA DE MÉXICO
FACULTAD DE INGENIERÍA
DIVISIÓN DE CIENCIAS BÁSICAS
COORDINACIÓN DE MATEMÁTICAS
El lado recto de una parábola es 4p , para el ejemplo se tiene que p = -1 ya que
 19 1 
 35 1 
4p = -4, vértice V  − ,  , Foco F  − , 
 16 2 
 16 2 
Ejemplo:
Determinar la ecuación ordinaria, vértice y foco de la parábola de ecuación
3x 2 − y + 6 x + 2 = 0
Resolución:
Agrupando y completando el trinomio al cuadrado perfecto
3( x 2 + 2 x) = y − 2
3( x 2 + 2 x + 1) = y − 2 + 3
simplificando y factorizando el miembro derecho de la ecuación
3( x + 1) 2 = y + 1
multiplicando por
( x + 1) 2 =
1
a la ecuación
3
y +1
3
1
1
Si el lado recto es 4p y en este caso 4p = , se tiene que p =
3
12
y +1
y tiene su eje focal
3
11 

paralelo al eje Y, con vértice en V( −1, −1) y foco F  −1, − 
12 

Por lo que la parábola tiene ecuación ( x + 1)2 =
Abril De 2011
8 de 8