Circuitos SC (Switched Capacitors)

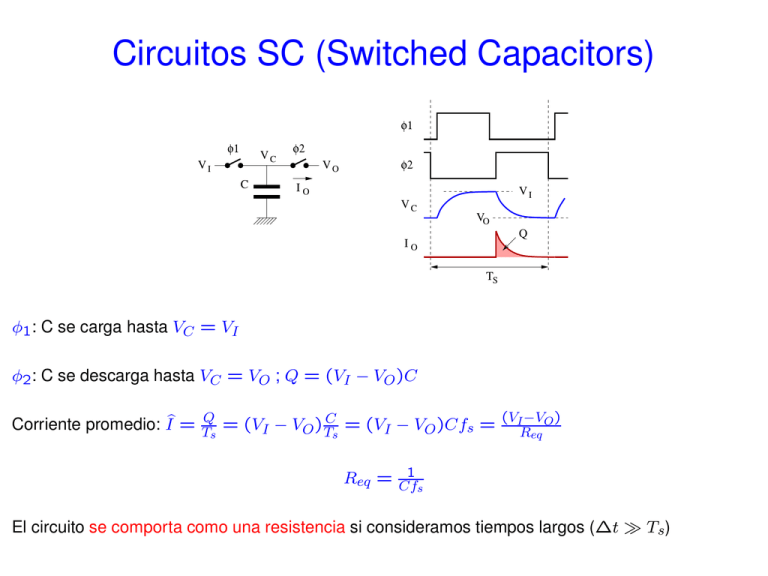
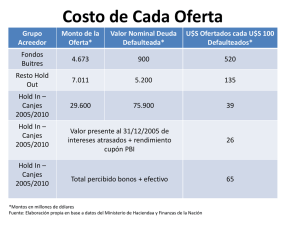
Circuitos SC (Switched Capacitors)
φ1
φ1
VC
VI
C
φ2
VO
IO
φ2
VC
VI
VO
IO
Q
TS
φ1 : C se carga hasta VC = VI
φ2 : C se descarga hasta VC = VO ; Q = (VI − VO )C
O)
Corriente promedio: Ib = TQs = (VI − VO ) TCs = (VI − VO )Cfs = (VIR−V
eq
1
Req = Cf
s
El circuito se comporta como una resistencia si consideramos tiempos largos (∆t T s)
Circuitos SC (Switched Capacitors)
Integrador de Tiempo Continuo
Integrador S. C.
C
C2
φ1
R
Vi
Vo
H(s) =
Av =
Vi
−1
RC s
−1
RC
VC
φ2
Vo
C1
H(s) =
Av =
−C1 fs
C2s
−C1
C2
fs
Tiempo continuo
- R y C son valores absolutos =>Variaciones grandes
- Se necesitan mecanismos de ajuste (sintonía)
S. C. (tiempo discreto)
- Cocientes de capacidades (C1/C2) =>valores precisos (sin sintonía)
La precisión sólo está limitada por el mismatch entre condensadores
- Ancho de banda proporcional a la frecuencia del reloj, f s
Sistemas de tiempo discreto (Muestreados)
fs > 2 × fmax (teorema de Shannon-Nyquist)
Análisis mediante transformada Z
z −1 ≡ retardo de un ciclo de reloj
Función de transferencia genérica:
−1 +···+a z −n
Y (z)
o+a1 z
n
H(z) = X(z)
= a1+b
−1+···+bm z −m
1z
Dominio del tiempo (xi : entrada en el ciclo actual, xi−n: entrada hace n ciclos):
Y + b1z −1Y + · · · + bm z −mY = a0X + · · · an z −nX
yi = a0 xi + a1 xi−1 + · · · + anxi−n
Respuesta en frecuencia: Evaluar H ejω/f s
→
− b1 yi−1 − b2yi−2 − · · · − bm yi−m
(sustitución: z ↔ ejω/f s )
Sistemas de tiempo discreto (Muestreados)
Ejemplo:
1+z −2
H(z) = 1−1,46 z −1+0,81 z −2
Lugar de las raíces
Respuesta en frecuencia (magnitud)
20
fs/4
+j
ω/fs
fs/2
jω /fs
0
fs
Ganancia (dB)
e
10
Ceros
0
Polos
-10
-20
−1
+1
−j
3fs/4
-30
-40
0
0.05
0.1
0.15 0.2 0.25 0.3 0.35
Frecuencia normalizada
0.4
0.45
0.5
Equivalencias Tiempo Continuo / Discreto
- Transformación de Euler
xi−xi−1
d
1
−1
X
sX ≡ dt x(t) ≈
≡ Ts 1 − z
Ts
1
−1
sustitución s ↔ Ts 1 − z
- Poco precisa para frecuencias altas (error en la fase ≡ retardo de 1/2 ciclo)
- Transformación bilineal
2 1 − z −1
s ↔
Ts 1 + z −1
- Más precisa (sin error en la fase)
- Aún así puede ser necesario el Prewarping en frecuencias altas:
ω0
Cambiar frecuencias de polos y ceros por ωpw = 2fs tan 2f
s
La respuesta en frecuencia es la misma en CT y DT para ω0
Integradores S.C.
- Bloque básico en filtros, convertidores A/D, etc.
C2
φ1
φ2
Vi
C1
C par
Sustr.
− C par se suma a C 1 => error
Vo
− Este circuito no se usa en la práctica
Integradores S.C.
Integrador Inversor
φ1
C2
Q
φ2
C1
Vi
φ1
C par2
φ2
φ2
φ1
C par1
Vo
Vo
Hold
Transp
instante de
muestreo
Hold
salida
válida
- Cpar2 siempre tiene la misma tensión => no transfiere carga => Sin error
fase φ1 : VC1 = 0
1
fase φ2 : VC1 = VI ; Q = ∆VC1 C1 = VI C1 ; ∆VO = −Q/C2 = −VI C
C2
C1
VO i = VO i−1 − VI i C
2
1
Vo = −C1
H(z) = V
C2 1−z −1
I
- Durante φ2 el integrador está transparente (Track & Hold)
Integradores S.C.
Integrador No Inversor (fases cruzadas)
φ1
C2
φ1
C1
Q
Vi
φ2
φ2
φ2
φ1
retardo
Vo
Vo
Hold
muestra i−1
Hold
Hold
muestra i
instante de muestreo salida válida
fase φ1 : VC1 = VI
1
fase φ2 : VC1 = 0 ; Q = ∆VC1 C1 = −VI C1 ; ∆VO = −Q/C2 = +VI C
C2
+C1 z −1/2
V
o
H(z) = V = C 1−z −1
2
I
- El integrador nunca está transparente => Sample & Hold
- El retardo de medio ciclo se traduce en un numerador z −1/2
Dinámica de los Integradores S.C.
- Fase 1. Carga de condensadores
C2
φ1
C1
φ1
φ2
Vi
Vi
φ2
r on
φ1
C
Verr
Vi
Vo
φ1
T1
r on
Vc
0
Verr = exp −T1
Vi
2 ron C
T1
; si VVerr = 10−4 entonces ron = 18,4
C
i
- Fase 2. Cambio en la salida del operacional
φ2
T2
TSR
TSet
∆VO2
∆VO
O
TSR = ∆V
SR
V err
VO
SLEW
RATE
SETTLING
; Verr = ∆VO2 exp (−BW TSet)
Verr = 10−4
Si ∆V
o2
queda:
2
; BW = GBW C C+C
1
2
GBW = T9,2
Set
1
1+C
C2
Dinámica de los Integradores S.C.
Ejemplo:
Datos de partida:
fs = 10 M Hz
TSR = TSet = 22,5 ns
T1 = 45 ns
C1 = C2 = 1 pF
Se obtiene:
ron < 2,4 kΩ
SR > 124 V /µs
GBW > 130 M Hz
T2 = 45 ns
∆Vo < 2,8 V
2
1
BIQUAD FLEISHER−LAKER
2
C
1
E
2
1
D
2
Vin
1
B
2
G
2
F
1
2
A
Vo
1
1
2
1
J
−2
z
1
2
H
−2
z
1 −
1
2
−2
z
1
2
A G
−
B D
I
B
−
J
+
B
I
B
A E
z
B D
−1
−2 −
F
B
+
A
C
B
D
+
E
D
+ 1+
F
B
2
I
1
B D
−1
+z
H(z)=
Vo’
2
B
A H
−
1
D B
−
H
D
−1 H
+z
D
1+
F
B
+
G
D
−
J
C
B D
+2
E
D
+
I
−2
z
1−
A E
B D
+z
−1
−2 −
F
B
+
A
C
B
D
+
E
D
1
- Permite implementar cualquier H(z) con numerador y denominador de 2 o grado
+ 1+
C
B D
H’(z)=
2
J
E J
F
B
+
E
D
−
G
D
1+
F
B
Circuitos SC. Simplificaciones
C1
mismas fases
C1
φ2
A
A
φ1
C
C2
C2
φ2
φ2
B
B
C
φ1
φ2
C
φ2
φ1
φ1
φ1
φ1
C
φ2
C
φ2
− C iguales
φ2
φ1
− Fases cruzadas y sin cruzar
Circuitos SC. Reglas de escalado
1.
Si todos los condensadores conectados a la salida de un operacional se multiplican por µ, la
amplitud de dicha salida se divide por µ y el resto no cambia. (útil para igualar amplitudes y
maximizar el rango dinámico)
2.
Si todos los condensadores conectados a la tierra virtual de un operacional se multiplican por µ,
las salidas no cambian (facilita la selección de valores para los condensadores)
3.
Si todos los condensadores conectados entre la entrada y tierras virtuales se multiplican por µ,
la ganancia del sistema se multiplica por µ (permite el ajuste final de la ganancia)