examen: integrales. cálculo de probabilidades. matemáticas

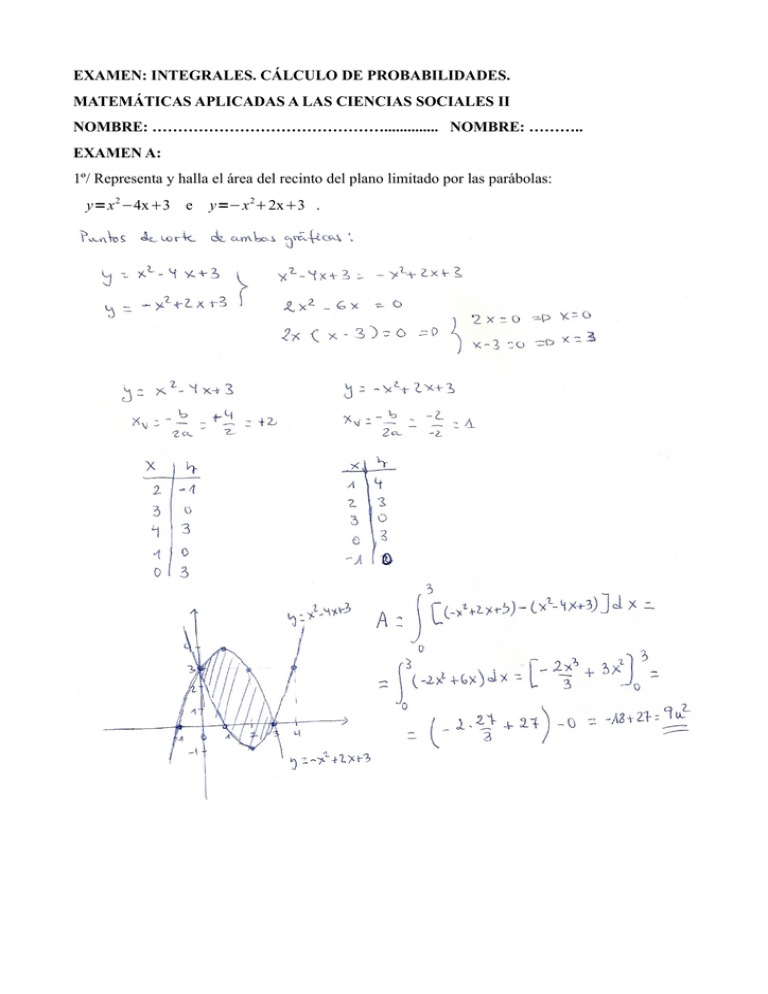
EXAMEN: INTEGRALES. CÁLCULO DE PROBABILIDADES.
MATEMÁTICAS APLICADAS A LAS CIENCIAS SOCIALES II
NOMBRE: ……………………………………….............. NOMBRE: ………..
EXAMEN A:
1º/ Representa y halla el área del recinto del plano limitado por las parábolas:
y=x 2 −4x3 e
y=−x 22x3 .
2º/ Se ha determinado que el 42% de los habitantes de una región son aficionados al fútbol y al
baloncesto, y que el 70% de los aficionados al fútbol, también son aficionados al baloncesto. ¿Qué
probabilidad hay de que elegida al azar una persona de dicha región resulte ser aficionada al fútbol?
3º/ En una empresa figuran en nómina un total de 1000 personas, de las cuales 350 son mujeres.
Sabiendo que los transportes públicos son utilizados para acudir al trabajo, por un 40% de los
varones, y no son utilizados por el 25% de las mujeres, obtener la probabilidad de que elegida al
azar una persona de dicha empresa, resulte ser usuaria de los transportes públicos para acudir al
trabajo.
4º/ El personal de cierta empresa está constituido por un 60% de personal obrero, un 25% de
personal técnico, siendo el resto personal administrativo. A todos los trabajadores de dicha empresa
se les pregunta si estarían dispuestos a admitir una reducción en el número de horas semanales de
trabajo con la consiguiente disminución económica de su nómina. Contestaron afirmativamente un
40% del personal obrero, un 30% del personal técnico y un 60% del personal administrativo. Si
seleccionamos al azar un trabajador de dicha empresa, determinar la probabilidad de que:
a)
b)
c)
Haya contestado afirmativamente.
Pertenezca al personal administrativo y haya contestado negativamente.
Sabiendo que es un trabajador del personal técnico, haya contestado negativamente.
5º/ Tenemos dos urnas. La primera con 2 bolas rojas y 3 bolas blancas, y la segunda con una bola
blanca y 4 rojas. Lanzamos un dado, si sale 1 ó 2, sacamos una bola de la primera urna. En caso
contrario, la extraemos de la segunda urna.
a)
¿Cuál es la probabilidad de sacar bola roja?
b)
Sabiendo que la bola extraída ha sido de color rojo, ¿cuál es la probabilidad de que
haya sido sacada de la primera urna?