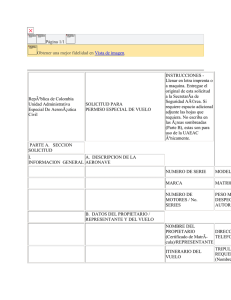
EVALUACIÓN DE LA ESTABILIDAD DEL AVIÓN NO TRIPULADO

Universidad Simón Bolívar
Decanato de Estudios de Postgrado
Maestría en Ingeniería Mecánica
EVALUACIÓN DE LA ESTABILIDAD DEL AVIÓN NO
TRIPULADO DE CONSERVACIÓN ECOLÓGICA (ANCE X-3)
Trabajo de Grado presentado a la Universidad Simón Bolívar por
Elsa María Cárdenas Álvarez
Como requisito parcial para optar al grado de:
Magíster en Ingeniería Mecánica
Realizado con la asesoría del Profesor
Andrea Amerio Helou
Mayo, 2008
i
ii
AGRADECIMIENTO
Se eleva un especial agradecimiento al Decanato de Investigación, Sede Litoral, y al
profesor Andrea Amerio por la guía y soporte brindado durante el inicio, desarrollo y fin de
este proyecto.
Extiendo también un agradecimiento a familiares y amigos, quienes me dieron el
ánimo necesario para culminar satisfactoriamente este trabajo de investigación, en especial a
mi esposo, por el apoyo que siempre me ha brindado.
iii
RESUMEN
En el año 2003 comenzó el desarrollo del diseño preliminar de una aeronave no
tripulada cuya función es la detección de derrames de crudo en zonas de extracción petrolera
por medio de una cámara. El diseño conceptual describe una aeronave de 182,055 kg de masa
de despegue, ala recta de 5,18 m de envergadura, doble botalón de cola, velocidad del crucero
de 41 m/s, propulsado por una hélice acoplada a un motor de pistón. Al diseño le han sido
realizados una serie de estudios y modificaciones para su mejora. El objetivo de este estudio es
evaluar la estabilidad estática y dinámica de la aeronave, empleando el método vortex lattice,
específicamente el código de fuente abierta Tornado versión 1.31, así como sus cualidades y
maniobrabilidad de vuelo. Durante el estudio se mantuvo fijo el número de Mach y fueron
evaluadas las derivadas de estabilidad estática de la aeronave para diferentes ángulos de
ataque, deslizamiento, deflexión de las superficies móviles; elevador, alerones y timón de
dirección y a diferentes velocidades angulares de rotación; longitudinal y latero-direccionales.
La rejilla empleada para simular la aeronave esta compuesto de superficies planas con
curvatura formada por 1100 paneles. El fuselaje fue modelado por medio de superficies
cruciformes. El modelo computacional utilizado en Tornado fue validado utilizando la versión
del ANCE X-2 del cual se tienen resultados previos obtenidos de ensayo en túnel de viento,
estos resultados fueron comparados los coeficientes de fuerzas aerodinámicos obtenidos
empleando los códigos PAN AIR (A502i) y Digital Datcom, mostrando una muy buena
correlación que para ángulos de ataque de operación de la aeronave. Las derivadas de
estabilidad obtenidas muestran que el ANCE es estable estáticamente en sus tres ejes de
movimiento. Dinámicamente se muestra estable en su eje longitudinal en los modos de
período corto y largo, así como latero – direccionalmente, a los modos de banqueo y de
banqueo holandés, mientras en espiral tiende a la inestabilidad. Las cualidades de vuelo del
aeroplano son de buenas a excelentes en sus modos de período corto y largo, de banqueo y
banqueo holandés, e insuficientes en el modo espiral, De este estudio se concluye que el
ANCE es lo suficientemente estable como para proseguir con el avance de diseño,
específicamente con el estudio del comportamiento dinámico de la aeronave en pruebas de
vuelo, de la respuesta obtenida de estas, se sugiere la implementación de un sistema de control
automático que permita corregir la amortiguación en espiral o discutir el rediseño del
empenaje de cola.
Palabras clave: Dinámica de fluidos computacional lineal, Aeronave no tripulada, Método
vortex lattice, Estabilidad estática, Estabilidad dinámica, Cualidades de vuelo.
iv
ÍNDICE
ACTA DE APROBACIÓN DEL JURADO ............................ ¡Error! Marcador no definido.
AGRADECIMIENTO ................................................................................................................ ii
RESUMEN ................................................................................................................................ iii
ÍNDICE.......................................................................................................................................iv
ÍNDICE DE TABLAS................................................................................................................vi
ÍNDICE DE FIGURAS ........................................................................................................... viii
LISTA DE SÍMBOLOS .............................................................................................................xi
INTRODUCCIÓN.......................................................................................................................1
CAPÍTULO I OBJETIVOS.........................................................................................................3
Objetivo General......................................................................................................................3
Objetivos Específicos ..............................................................................................................3
CAPÍTULO II EL AVIÓN NO TRIPULADO DE CONSERVACIÓN ECOLÓGICA.............4
CAPÍTULO III ESTABILIDAD ESTÁTICA DE UNA AERONAVE......................................8
Estudio de la Estabilidad Estática............................................................................................9
Estabilidad Estática Longitudinal............................................................................................9
Estabilidad Estática Latero – Direccional .............................................................................16
CAPÍTULO IV ESTIMACIÓN DE LAS DERIVADAS DE ESTABILIDAD........................23
Derivadas de Estabilidad Longitudinal..................................................................................23
Derivadas de Estabilidad Latero Direccional ........................................................................24
Estimación de los Coeficientes de Estabilidad ......................................................................24
Resultados de los Coeficientes de Estabilidad ......................................................................37
CAPÍTULO V ESTABILIDAD DINÁMICA DE UNA AERONAVE....................................39
Estabilidad Dinámica Longitudinal .......................................................................................40
Estabilidad Dinámica Latero – Direccional...........................................................................48
v
CAPÍTULO VI CUALIDADES DE VUELO Y MANIOBRABILIDAD DE UNA
AERONAVE .............................................................................................................................54
Clasificación de las Aeronaves para Calificar sus Cualidades de Vuelo ..............................56
Análisis de las Cualidades de Vuelo de una Aeronave .........................................................58
CAPÍTULO VII RESULTADOS Y DISCUSIÓN....................................................................65
Estimación de las Derivadas de Estabilidad ..........................................................................65
Estudio Dinámico ..................................................................................................................66
Cualidades y Maniobra de Vuelo de la Aeronave .................................................................71
CAPÍTULO VIII CONCLUSIONES ........................................................................................79
REFERENCIAS BIBLIOGRÁFICAS ......................................................................................81
APÉNDICE A SISTEMA REFERENCIAL DE COORDENADAS DE LA AERONAVE ....84
vi
ÍNDICE DE TABLAS
Tabla 4.1: Derivadas de estabilidad longitudinal. .....................................................................23
Tabla 4.2: Derivadas de estabilidad latero –direccional............................................................24
Tabla 4.3: Comparación de los parámetros de la curva de sustentación del modelo ANCE X-2
obtenidos por los diferentes métodos. .......................................................................................32
Tabla 4.4: Comparación de los parámetros de la curva polar y de la curva de coeficiente de
resistencia en función del coeficiente de sustentación al cuadrado, del modelo ANCE X-2,
obtenidos de los diferentes métodos..........................................................................................34
Tabla 4.5: Control de las variables de estudio...........................................................................36
Tabla 4.6: Coeficientes de estabilidad de la aeronave...............................................................38
Tabla 6.1: Requerimientos de amortiguamiento en período largo para toda clase de aeronave.
Fuente: Hodgkinson (1998). ......................................................................................................62
Tabla 6.2: Requerimientos de amortiguamiento en modo de banqueo, máximo tiempo
constante (1/σ) en segundos. Fuente: Hodgkinson (1998). .......................................................63
Tabla 6.3: Requerimientos de amortiguamiento para el modo Espiral, mínimo tiempo para
doblar la amplitud en segundos. Fuente: Hodgkinson (1998). ..................................................63
Tabla 6.4: Requerimientos de Frecuencia y Amortiguamiento en el Modo de Banqueo
Holandés. Fuente: Hodgkinson (1998)......................................................................................64
Tabla 7.1: Coeficientes aerodinámicos del ANCE X-3 y criterios de estabilidad. ...................65
Tabla 7.2: Derivadas de Estabilidad Longitudinal. ...................................................................66
Tabla 7.3: Derivadas de Estabilidad Latero –Direccional.........................................................66
Tabla 7.4: Aproximaciones longitudinales en período corto.....................................................67
Tabla 7.5: Aproximaciones longitudinales en período largo.....................................................68
Tabla 7.6: Comparación de métodos aproximados y solución exacta al modo longitudinal. ...68
Tabla 7.7: Métodos aproximados al modo espiral.....................................................................69
vii
Tabla 7.8: Aproximación al modo de banqueo..........................................................................70
Tabla 7.9: Aproximación al modo de banqueo holandés. .........................................................70
Tabla 7.10: Comparación de métodos aproximados y solución exacta al modo latero –
direccional. ................................................................................................................................71
Tabla 7.11: Parámetros representativos del estudio longitudinal. .............................................72
viii
ÍNDICE DE FIGURAS
Figura 2.1: Vista esquemática de planta superior, perfil y frente del ANCE X-0.......................5
Figura 2.2: Vista esquemática de planta superior, planta invertida, perfil y frente del ANCE X1. ..................................................................................................................................................6
Figura 2.3: Vista esquemática de planta superior, planta invertida, perfil y frente del ANCE X3. ..................................................................................................................................................7
Figura 3.1: Ejes de movimiento y velocidades angulares de una aeronave. ...............................8
Figura 3.2: Principales superficies de control de una aeronave. .................................................9
Figura 3.3: Diagrama de cuerpo libre del ala mostrando su contribución al momento de
cabeceo. .....................................................................................................................................10
Figura 3.4: Diagrama de cuerpo libre ala – estabilizador horizontal mostrando la contribución
de la cola al momento de cabeceo. ............................................................................................12
Figura 3.5: Vista en planta y de perfil del fuselaje de un aeroplano. ........................................15
Figura 3.6: Fuerza de desbalance y deslizamiento resultante producido por una perturbación en
banqueo......................................................................................................................................19
Figura 3.7: Contribución del Diedro a la Estabilidad de de Banqueo. ......................................20
Figura 3.8: Contribución a la Estabilidad de Banqueo de la interacción Ala – Fuselaje. .........21
Figura 4.1: Rejilla de vórtices del ANCE X-2 utilizado en la simulación con el código Tornado
Vortex Lattice. ...........................................................................................................................26
Figura 4.2: Geometría de los paneles del ANCE X-2 utilizado en la simulación con el código
PAN AIR sin las ondas..............................................................................................................29
Figura 4.3: Geometría de los paneles del ANCE X-2 utilizado en la simulación con el código
PAN AIR mostrando las ondas..................................................................................................29
Figura 4.4: Curvas del coeficiente de sustentación en función del ángulo de ataque del ANCE
X-2 obtenidas con Tornado, Digital Datcom, PAN AIR y ensayos en túnel del viento. ..........31
ix
Figura 4.5: Curvas del coeficiente de sustentación en función del coeficiente de resistencia del
ANCE X-2 obtenidas con Tornado, Digital Datcom, PAN AIR y ensayos en túnel del viento.
...................................................................................................................................................33
Figura 4.6: Pendientes del coeficiente de resistencia en función del coeficiente de sustentación
al cuadrado del ANCE X-2 obtenidas con Tornado, Digital Datcom, PAN AIR y ensayos en
túnel del viento. .........................................................................................................................34
Figura 4.7: Curvas del coeficiente de momento en función del ángulo de ataque del ANCE X2, obtenidos con los códigos Tornado, Digital Datcom y PAN AIR.........................................35
Figura 4.8: Rejilla de vórtices del ANCE X–3 utilizado en la simulación con el código
Tornado......................................................................................................................................36
Figura 5.1: Representación gráfica de Estabilidad e Inestabilidad Dinámica. ..........................39
Figura 5.2: Modelo Restringido a Movimiento Puramente de Cabeceo. ..................................40
Figura 5.3: Sistema mecánico de amortiguación.......................................................................42
Figura 5.4: Modo de Período Largo. .........................................................................................46
Figura 5.5: Movimiento Oscilatorio de Período Corto..............................................................47
Figura 5.6: Movimientos de Divergencia espiral y Divergencia Direccional. ..........................51
Figura 5.7: Respuesta de banqueo al efectuar una deflexión en los alerones............................51
Figura 5.8: Movimiento Banqueo Holandés..............................................................................52
Figura 6.1: Escala de clasificación Cooper y Harper, de las cualidades de vuelo.....................55
Figura 6.2: Requerimientos de frecuencia y amortiguamiento en período corto, para categoría
de vuelo B y aeronaves de todas las clases. Fuente: Hodgkinson (1998). ................................59
Figura 6.3: Requerimientos de frecuencia y amortiguamiento en período corto, para categoría
de vuelo C y aeronaves de clase I y II. Fuente: Hodgkinson (1998).........................................60
Figura 6.4: Requerimientos de frecuencia y amortiguamiento en período corto, para fases de
vuelo de categoría B y aeronaves de todas las clases. Fuente: Hodgkinson (1998)..................61
x
Figura 6.5: Requerimientos de amortiguamiento y frecuencia en período corto, para categoría
C y aeronaves de todas las clases con una aceleración sensitiva mayor a 5g/rad. Fuente:
Hodgkinson (1998). ...................................................................................................................62
Figura 7.1: Localización del nivel de cualidad de vuelo en período corto para la categoría de
vuelo B del ANCE X-3 sin potencia. ........................................................................................73
Figura 7.2: Localización del nivel de cualidad de vuelo en período corto para la categoría de
vuelo C del ANCE X-3 sin potencia. ........................................................................................74
Figura 7.3: Localización del nivel de cualidad de vuelo en período corto para la categoría de
vuelo B del ANCE X-3 sin potencia. ........................................................................................75
Figura 7.4: Localización del nivel de cualidad de vuelo en período corto para categoría de
vuelo C del ANCE X-3 sin potencia con una aceleración sensitiva mayor a 5g/rad. ...............76
Figura A.1: Sistema de referencia de coordenadas utilizado por Robert Nelson. Fuente: Nelson
(1998). .......................................................................................................................................84
Figura A.2: Sistema de coordenadas, convención de signos para ángulos y momentos
aerodinámicos actuantes en una aeronave en vuelo libre. Fuente: Phillips (2004). ..................85
Figura A.3: Sistemas de coordenadas en una aeronave en vuelo libre empleado en el código
Tornado Vortex Lattice. Fuente: Melin (2000a). ......................................................................86
Figura A.4: Sistemas de coordenadas, convención de signos para ángulos y momentos
aerodinámicos actuantes en una aeronave en vuelo libre empleado en el software PAN AIR.
Fuente: Sidwell, et al (1990)......................................................................................................86
Figura A.5: Sistema de referencia de coordenadas utilizadas para el estudio del ANCE. ........87
xi
LISTA DE SÍMBOLOS
AR
=
alargamiento.
an
=
coeficiente de la serie de Fourier.
b
=
envergadura.
CAP
=
parámetro de anticipación.
CD
=
coeficiente de resistencia del aeroplano.
CDcp
=
coeficiente de resistencia del aeroplano con potencia o vuelo propulsado.
C Do
=
coeficiente de resistencia mínimo.
CDu
=
variación del coeficiente de resistencia respecto a la velocidad.
C D ,α
=
variación del coeficiente de resistencia en respecto al ángulo de ataque.
CL
=
coeficiente de sustentación del aeroplano.
CLMAX =
coeficiente de sustentación máximo del aeroplano.
C Lo
=
coeficiente de sustentación para ángulo de ataque cero.
C Lt
=
coeficiente de sustentación del estabilizador horizontal.
CLw
=
coeficiente de sustentación del ala.
C L v ,α =
C L ,q
=
pendiente de la curva de sustentación de la cola.
coeficiente de estabilidad adimensional de sustentación respecto de la velocidad
angular longitudinal.
C L ,t
=
coeficiente de sustentación del estabilizador horizontal.
C L ,α
=
pendiente de la curva de sustentación.
CL,α w =
C L ,α&
=
C L ,δ e =
pendiente de la curva de sustentación del ala.
pendiente de la curva de sustentación respecto a la derivada del ángulo de ataque.
pendiente de la curva de sustentación respecto de la deflexión del elevador.
Cl
=
coeficiente de momento de banqueo de la aeronave.
Cl, p
=
variación del coeficiente de momento de banqueo respecto a la velocidad angular
de banqueo.
Cl,r
=
coeficiente de estabilidad adimensional de momento de banqueo respeto de la
xii
velocidad angular direccional.
Cl , β
=
C l ,δ a =
coeficiente de momento de banqueo respecto al ángulo de deslizamiento.
variación del coeficiente de momento de banqueo respecto a la deflexión de los
alerones.
C l,δ r
=
variación del coeficiente de momento de banqueo respecto a la deflexión del
timón de dirección.
Cm
=
coeficiente de momento.
Cm,0
=
coeficiente de momento para ángulo de ataque cero.
Cm,0w =
coeficiente de momento del ala para ángulo de ataque cero.
Cm acw =
coeficiente de momento del ala respecto al centro aerodinámico.
Cm,q
=
coeficiente de momento de cabeceo respecto a la velocidad angular de cabeceo.
Cm,t
=
coeficiente de momento de cabeceo aportado por el estabilizador horizontal.
Cm,u
=
coeficiente de momento de cabeceo respecto a la velocidad en el eje x.
Cm,α
=
coeficiente de momento de cabeceo respecto al ángulo de ataque.
Cm,α t =
coeficiente de momento de cabeceo del estabilizador horizontal.
Cm,α&
=
coeficiente de momento de cabeceo respecto a la derivada del ángulo de ataque.
Cm,δe
=
coeficiente de momento de cabeceo respecto a la deflexión del elevador.
Cm,δr
=
coeficiente de momento de la cola vertical con respecto a la deflexión del timón de
dirección.
C nf
=
coeficiente de momento de guiñada aportado por el fuselaje.
C n, p
=
variación del coeficiente de momento de guiñada respecto a la velocidad angular
de banqueo.
Cn,r
=
variación del coeficiente de momento de guiñada respecto a la velocidad angular
de guiñada.
Cn , β
=
coeficiente de momento de guiñada en función del ángulo de deslizamiento.
Cn,δa
=
variación del coeficiente de momento de guiñada respecto a la deflexión de los
alerones.
Cn,δr
=
variación del coeficiente de momento de guiñada respecto a la deflexión del timón
de dirección.
xiii
CY , p
=
variación del coeficiente de fuerza en el eje y, respecto a la velocidad angular de
banqueo.
CY , r
=
variación del coeficiente de fuerza en el eje y, respecto a la velocidad angular
guiñada.
=
variación del coeficiente de fuerza en el eje y, respecto al ángulo de deslizamiento.
CY ,δ a =
variación del coeficiente de fuerza lateral en función de la deflexión de los
CY , β
alerones.
CY ,δ r =
variación del coeficiente de fuerza en el eje y, respecto a la deflexión del timón de
dirección.
c
=
cuerda media del ala.
cf
=
longitud total del fuselaje.
cl
=
coeficiente de sustentación del perfil.
cl,α
=
pendiente de la curva de sustentación del perfil.
co
=
cuerda del ala en el encastre.
ct
=
cuerda del ala en el borde externo o punta.
cv
=
cuerda media del estabilizador vertical.
D
=
fuerza de resistencia aerodinámica.
Dt
=
fuerza de resistencia aerodinámica aportada por el estabilizador horizontal.
Dw
=
fuerza de resistencia del ala.
df
=
diámetro de igual área a Sf.
e
=
coeficiente de eficiencia de Oswald.
I
=
matriz identidad.
IX
=
momento de Inercia en el eje x.
IY
=
momento de inercia en ele eje y.
IZ
=
momento de inercia en el eje z.
iw
=
ángulo de incidencia del ala.
it
=
ángulo de incidencia del estabilizador horizontal.
kl
=
relación de la derivada de estabilidad de banqueo.
L
=
fuerza aerodinámica de sustentación.
Lp
=
variación del momento de banqueo respecto a la velocidad angular sobre el eje x.
xiv
Lr
=
variación del momento de banqueo respecto a la velocidad angular sobre el eje z.
Lδa
=
variación del momento de banqueo respecto a la deflexión de los alerones.
Lδr
=
variación del momento de banqueo respecto a la deflexión del timón de dirección.
ℓ
=
momento de banqueo.
ℓt
=
sustentación generada por el estabilizador horizontal.
ℓw
=
sustentación del ala.
ℓβ
=
variación del momento de banqueo respecto al ángulo de deslizamiento.
lf
=
distancia a la que está el centro de presión del fuselaje por detrás del centro de
gravedad de la aeronave.
lt
=
distancia entre el centro de gravedad de la aeronave y el centro aerodinámico del
estabilizador horizontal.
lv
=
distancia entre el centro de gravedad de la aeronave y el centro aerodinámico del
estabilizador vertical.
M
=
momento.
MACW =
momento del ala producido alrededor del centro aerodinámico del ala.
Mcgw
=
momento del ala alrededor del centro de gravedad del aeronave.
Mact
=
momento de la cola producido alrededor del centro aerodinámico del ala.
Mq
=
variación momento respecto a la velocidad angular longitudinal.
Mu
=
variación de momentos respecto a la velocidad lineal en x.
Mα
=
variación de Momento respecto al ángulo de ataque.
M α&
=
variación de momento respecto a la derivada del ángulo de ataque.
Mδe
=
variación de momento respecto a la deflexión del elevador.
MδT
=
variación de momento respecto a la variación de empuje.
Mω
=
variación de momentos, respecto al componente de la velocidad en z.
M ω&
=
variación de momento respecto a la aceleración en eje z.
Np
=
variación del momento de guiñada respecto a la velocidad angular sobre el eje x.
Nr
=
variación del momento de guiñada respecto a la velocidad angular sobre el eje z.
Nβ
=
variación del momento de guiñada respecto al ángulo de deslizamiento.
Nδa
=
variación del momento de guiñada respecto a la deflexión de los alerones.
Nδr
=
variación del momento de guiñada respecto a la deflexión del timón de dirección.
N1/2
=
número de ciclos para llevar la amplitud inicial de la perturbación a la mitad.
xv
N2
=
número de ciclos para llevar la amplitud inicial de la perturbación al doble.
n
=
momento de guiñada.
ncgf
=
momento de guiñada proporcionado por el fuselaje con respecto al centro de
gravedad.
n/α
=
aceleración sensitiva.
Pij
=
autovector correspondiente al jth autovalor.
Pm
=
potencia máxima promedio de la planta propulsora.
p
=
velocidad angular de banqueo.
Q
=
presión dinámica de aire, Q =
q
=
velocidad angular de cabeceo.
Re
=
número de Reynolds.
r
=
velocidad angular de guiñada.
S
=
superficie del ala.
Sf
=
área máxima de la sección transversal del fuselaje.
ST
=
superficie del estabilizador horizontal.
Sv
=
superficie del estabilizador vertical.
T
=
período.
t1/2
=
tiempo para llevar la amplitud inicial de la perturbación a la mitad.
t2
=
tiempo para llevar la amplitud inicial de la perturbación al doble.
U
=
velocidad de la corriente libre.
u
=
velocidad en el eje x.
VH
=
coeficiente de volumen del estabilizador horizontal.
Vv
=
coeficiente de volumen del estabilizador vertical.
W
=
peso.
w
=
velocidad en el eje z.
Xcg
=
coordenada del punto de centro de gravedad en porcentaje de la cuerda.
Xac
=
coordenada del punto de centro aerodinámico en porcentaje de la cuerda.
Xu
=
variación de las fuerzas en el eje x respecto a la velocidad lineal.
XδT
=
variación de las fuerzas en el eje x respecto a la variación de empuje.
Xω
=
variación de las fuerzas en el eje x respecto al componente de la velocidad en z.
1
⋅ ρ ⋅U 2
2
xvi
Yp
=
variación de las fuerzas en Y respecto a la velocidad angular sobre el eje x.
Yr
=
variación de las fuerzas en Y respecto a la velocidad angular sobre el eje z.
Yβ
=
variación de las fuerzas en y respecto al ángulo de deslizamiento.
Yδa
=
variación de las fuerzas en y respecto a la deflexión de los alerones.
Yδr
=
variación de las fuerzas en y respecto a la deflexión del timón de dirección.
Zcg
=
altura desde la referencia del fuselaje hasta el centro de gravedad.
Zcgt
=
altura desde la referencia del estabilizador horizontal hasta el centro de gravedad.
Zq
=
variación de fuerzas en el eje Z, respecto a la velocidad angular longitudinal.
Zu
=
variación de las fuerzas en el eje z respecto a la velocidad lineal.
Zα
=
variación de fuerzas en el eje Z respecto al ángulo de ataque.
Zα&
=
variación de fuerzas en z respecto a la derivada en función del tiempo del ángulo
de ataque.
Zδe
=
variación de fuerzas en e eje Z, respecto a la deflexión del elevador.
ZδT
=
variación de fuerzas en e eje Z, respecto a la variación de empuje.
Zω
=
variación de las fuerzas en el eje Z respecto al componente de la velocidad en z.
Zω&
=
variación de las fuerzas en z respecto a la aceleración en el eje z.
α
=
ángulo de ataque.
α0
=
ángulo de ataque para sustentación cero.
αf
=
ángulo de ataque del fuselaje.
αw
=
ángulo de ataque del ala.
β
=
ángulo de deslizamiento.
δa
=
ángulo de deflexión del alerón.
δe
=
ángulo de deflexión del timón de profundidad.
δr
=
ángulo de deflexión del timón de dirección.
δT
=
variación de empuje.
εr
=
efectividad del timón de dirección.
εs
=
ángulo lateral inducido en el timón de dirección.
εso
=
ángulo lateral inducido para ángulo de deslizamiento cero.
εs,β
=
ángulo lateral inducido en función del ángulo de deslizamiento.
ζ
=
relación de amortiguamiento.
ζbh
=
relación de amortiguamiento en modo de banqueo holandés.
xvii
ζnsp
=
relación de amortiguamiento en período corto.
ηv
=
eficiencia del estabilizador vertical, es igual a la relación entre las presiones
dinámicas entre la cola y el ala.
ηt
=
eficiencia del estabilizador horizontal.
θ
=
ángulo de cabeceo.
λ
=
autovalor o raíz.
Г
=
ángulo de diedro del ala.
ρ
=
densidad del aire.
σ
=
tasa o variación de amortiguamiento.
σr
=
tasa de amortiguamiento en modo de banqueo.
σs
=
tasa de amortiguamiento en modo espiral.
τ
=
tiempo constante de banqueo.
Φ
=
ángulo de banqueo de la aeronave.
ωd
=
frecuencia natural amortiguada.
ωn
=
frecuencia natural no amortiguada.
ωnsp
=
frecuencia natural no amortiguada en período corto.
ωnbh
=
frecuencia natural no amortiguada en modo de banqueo holandés.
dε
dα
=
relación de cambio del ángulo de aguas abajo respecto al ángulo de ataque.
1
INTRODUCCIÓN
El diseño de una aeronave no debe pasar inadvertido el análisis de la estabilidad
estática, su respuesta dinámica y las características de maniobrabilidad que posee. Estas
características pueden determinar desde el grado de eficiencia que demostrará el aeroplano
para cumplir la labor para la que se está diseñando, hasta la posible pérdida en vuelo luego de
realizar una maniobra.
El Avión No Tripulado de Conservación Ecológica (ANCE) tiene como misión la
detección temprana de derrames de crudo en zonas de extracción petrolera venezolana. El
diseño conceptual fue culminado en el año 2003, y describe un aeroplano monoplano de doble
botalón de cola con hélice propulsora acoplada a un motor de pistón, con ala recta rectangular
alta de 5,27 m de envergadura y 0,604 m de cuerda, con una longitud de 4,74 m y masa
máxima de despegue de 182,055 kg. Su velocidad de crucero es de 46,77 m/s, el techo de
servicio de operación fijado es de 2500 m. Los criterios de diseño utilizados con la finalidad
de hacer a la aeronave lo suficientemente estable para cumplir su misión fueron analíticos y
empíricos, y la estimación de las características de estabilidad estática por métodos analítico –
empíricos. (Boschetti y Cárdenas, 2003). Desde entonces las mejoras realizadas al aeroplano
han sido destinadas al aumento de la eficiencia aerodinámica. De esta forma se ha logrado
obtener una buena aproximación del comportamiento aerodinámico del artefacto por medio de
métodos experimentales y numéricos. (Cárdenas, et al, 2005, Boschetti, et al, 2006, Boschetti,
et al, 2008a)
Conociendo el comportamiento aerodinámico del ANCE, se hace necesario obtener un
acercamiento mas real de sus características de estabilidad empleando métodos mas avanzados
y profundizar en el análisis de los datos, con el fin de conocer el comportamiento estático y
dinámico, con mando fijo y sin potencia, al que tiende la aeronave luego de ser sometida a una
perturbación en su estado de vuelo de equilibrio.
2
Los coeficientes de fuerzas y momentos actuantes en la aeronave serán obtenidos
haciendo uso del código Tornado. El modelo computacional será validado a través de
resultados obtenidos del software PAN AIR, Digital Datcom y resultados obtenidos de
ensayos en el túnel de viento.
El desenvolvimiento dinámico del ANCE será analizado desacoplando su
comportamiento en longitudinal y latero – direccional, en su respuesta longitudinal serán
analizados los modos oscilatorios de período corto y de período largo, y en su respuesta latero
direccional los modos de banqueo, de espiral y de banqueo holandés. Para el estudio de estos
modos serán obtenidas sus características principales; frecuencia natural amortiguada y no
amortiguada, relación de amortiguamiento, tasa de amortiguamiento, tiempo para doblar la
amplitud, entre otras, con los que serán evaluadas las cualidades de vuelo de la aeronave.
Este estudio revelará si el ANCE es lo suficientemente estable como para proseguir
con el avance del diseño, o si es necesario detenerse a realizar algunos cambios en las
características físicas de la aeronave.
3
CAPÍTULO I
OBJETIVOS
Objetivo General
Evaluar la estabilidad estática y dinámica con mando fijo y sin potencia del Avión No
Tripulado de Conservación Ecológica (ANCE X-3).
Objetivos Específicos
Obtener las derivadas de estabilidad estática con mando fijo y sin potencia de la
aeronave.
Obtener la respuesta dinámica longitudinal y latero-direccional de la aeronave con
mando fijo y sin potencia.
Evaluar las cualidades de vuelo de la aeronave.
4
CAPÍTULO II
EL AVIÓN NO TRIPULADO DE CONSERVACIÓN ECOLÓGICA
El diseño del Avión No Tripulado de Conservación Ecológica (ANCE) tiene sus
inicios en el año 2002, con el concepto de un avión de reconocimiento aéreo para la búsqueda
y detección temprana de derrames petroleros en zonas de extracción venezolanas, bajo este
diseño conceptual surge el ANCE X-0, un aeronave monoplano de doble botalón de cola con
hélice impulsora, con las siguientes dimensiones; 4,74 m de longitud, envergadura de 5,27 m,
altura de 0,93 m y superficie de ala de 3,13 m2. La figura 1.1 muestra una vista esquemática de
planta superior, perfil y frente del ANCE X-0. La masa máxima de despegue estimada es de
182,055 kg, la masa en vacío 123,28 kg, la masa de carga de pago de 40 kg y la carga máxima
de combustible de 28,33 kg (Boschetti y Cárdenas, 2003).
Para su propulsión fue seleccionado un motor Cuyuna 460 FE-35 de dos tiempos con
dos pistones lineales de 35 hp (26,10 kW) a 6000 rpm, enfriado por aire por medio de un
ventilador interno, y con una temperatura máxima promedio de 205ºC (Two Stroke
International, 2001), alimentado con una mezcla de aceite para motor de dos tiempos y
gasolina mayor a 92 octanos. A este motor le es acoplado a una hélice 5868-9, Clark Y bipala
de 91,5 cm. de diámetro.
5
Figura 2.1: Vista esquemática de planta superior, perfil y frente del ANCE X-0.
Las actuaciones estimadas, de este diseño conceptual son: velocidad de crucero de
46,77 m/s, velocidad de entrada en pérdida de 28,66 m/s, y velocidad máxima de 62,91 m/s
ambas a nivel del mar. El techo de servicio de operación fijado fue de 2.500 m donde la
velocidad de entrada en pérdida se reduce a 25,84 m/s. Según cálculos preliminares se
determinó que la carrera de despegue sería de 377,3 m y la pista necesaria para el aterrizaje de
428,5 m. El rango máximo de operación estimado fue de 344,35 km. y el tiempo máximo de
vuelo de 11 horas, 12 minutos.
Con la finalidad de disminuir la masa estructural esta versión sufre un ligero cambio en
la forma transversal del fuselaje, pasando de ser rectangular a trapezoidal, lo que trae consigo
una disminución de la envergadura geométrica a 5,187 m; además de una reducción de su
longitud a 4,65 m. Adicionalmente se aumentó el tamaño de la hélice a 1,015 m como parte de
una nueva iteración en los datos del diseño. La figura 2.2 muestra un bosquejo de este diseño.
6
Figura 2.2: Vista esquemática de planta superior, planta invertida, perfil y frente del ANCE
X-1.
Teniendo como objetivo disminuir la resistencia viscosa de la aeronave se colocó un
spinner cilíndrico en la punta de la hélice y al tren de aterrizaje se le colocó un carenado
(Cárdenas, et al, 2005), esto le da paso a la nueva versión de la aeronave ANCE X-2. A esta
nueva adaptación de la aeronave le fue aplicado un alabeo local entre las estaciones del ala;
2,5135 y 2,5935 (medido en metros) en la porción entre el borde de fuga y el 80 por ciento de
la cuerda del ala. Estas modificaciones produjeron al ANCE X-3 con un aumento total de la
eficiencia en vuelo de crucero de planeo de 6,26 por ciento al ser estimado por el método
teórico, y de 4,745 por ciento de acuerdo a los resultados experimentales, y una disminución
de la resistencia en la misma condición de operación de 0,0035 (7,33%) calculada
teóricamente, y de 0,0022 (4,53%) medida experimentalmente (Boschetti, 2006), la figura 2.3
muestra una vista esquemática del ANCE X-3.
7
Figura 2.3: Vista esquemática de planta superior, planta invertida, perfil y frente del ANCE
X-3.
8
CAPÍTULO III
ESTABILIDAD ESTÁTICA DE UNA AERONAVE
La estabilidad de una aeronave se ve reflejada en la capacidad que esta tiene de volver
a su estado de equilibrio luego de presentar alguna perturbación, que puede ser ejercida desde
los mandos de vuelo o por condiciones atmosféricas; tales como ráfagas de viento o
turbulencias en el aire (Phillips, 2004). El estudio de la estabilidad de una aeronave se divide
en estático y dinámico, el estudio estático se refiere a la tendencia que presenta una aeronave a
volver o no a su equilibrio y el dinámico estudia este comportamiento en función del tiempo
(Nelson, 1998). Este estudio es además dividido en los principales ejes de movimiento de la
aeronave; longitudinal (x) el cual efectúa el movimiento de cabeceo (q) girando alrededor del
eje y, lateral (y), que girando alrededor del eje x produce un movimiento de alabeo (p),
direccional (z) alrededor del cual la aeronave realiza el movimiento de guiñada (r), y en la
interacción latero-direccional. En la figura 3.1, pueden observarse los ejes de movimiento de
la aeronave.
Figura 3.1: Ejes de movimiento y velocidades angulares de una aeronave.
Movimientos de una aeronave en vuelo
Las superficies de control de una aeronave normalmente son constituidas por; alerones,
elevador y timón de dirección, estos pueden ser observados en la figura 3.2, los alerones son
9
utilizados para controlar el momento de banqueo, el elevador para controlar el momento de
cabeceo y el timón de dirección para controlar el momento de guiñada.
Figura 3.2: Principales superficies de control de una aeronave.
El momento de cabeceo se realiza alrededor del eje lateral “y”, este surge como
resultado de la sustentación y la resistencia actuantes en la aeronave, en este estudio se tomará
como positivo la dirección nariz arriba. El momento de banqueo lo realiza la aeronave
alrededor del eje “x”, este es el resultado de la diferencia de sustentación en las semialas
generada por los alerones, este será positivo cuando el ala derecha de la aeronave baja; y el
momento de guiñada se realiza alrededor del eje vertical de la aeronave “z”, un momento
positivo tiende a rotar la nariz a la derecha del piloto.
Estudio de la Estabilidad Estática
El estudio de la estabilidad estática se realiza asumiendo que no hay aceleración en la
aeronave, un vuelo no acelerado requiere que la sumatoria de fuerzas y momentos actuantes en
la aeronave sean cero, esto es sustentación igual a peso, empuje igual a resistencia, y
momentos alrededor del centro de gravedad, en banqueo, cabeceo y guiñada deben ser igual a
cero.
Estabilidad Estática Longitudinal
Se dice que una aeronave esta provista de estabilidad estática longitudinal, cuando la
curva del coeficiente de momento de cabeceo (Cmα) de la aeronave es negativa. Si se trabaja
10
con la curva coeficiente de momento versus coeficiente de sustentación, el criterio de
estabilidad estática longitudinal se expresa como en la ecuación 3.1.
dC m
<0
dC L
(3.1)
La estabilidad longitudinal de una aeronave puede estudiarse, obteniendo
separadamente, la contribución que hacen los componentes que la conforman y luego
sumando cada uno de estos resultados “este método generalmente es exacto para diseños
preliminares, y muestra la relación entre los coeficientes de estabilidad, la geometría y las
características de la aeronave” (Nelson, 1998) y sólo es valido para regímenes de vuelo
subsónico.
Los principales componentes que se analizan en el estudio de la estabilidad estática
longitudinal de una aeronave son; ala, fuselaje, cola y sistemas de propulsión.
Contribución del Ala
Si estudiamos el ala de una aeronave estáticamente, del diagrama de cuerpo libre
mostrado en la figura 3.3 puede ser obtenida la ecuación 3.2.
Figura 3.3: Diagrama de cuerpo libre del ala mostrando su contribución al momento de
cabeceo.
∑M
cgw
[
]
[
= Lw cos(α w − i w ) X cg − X ac + D w sen(α w − i w ) X cg − X ac
[ ]
[ ]
+ L w sen(α w − i w ) Z cg − D w cos(α w − i w ) Z cg + Macw
]
(3.2)
Simplificando y adimensionalizando, se obtiene el coeficiente de momento respecto
del centro de gravedad del ala, mostrado en la ecuación 3.3.
11
 X cg X ac 

C m,cgw = C m,acw + C L w 
−
c
c


(3.3)
El coeficiente de momento del ala respecto al centro aerodinámico (Cm,acw) es obtenido
de las curvas del perfil correspondientes al ala de la aeronave, teniendo como dato de entrada
el ángulo de incidencia, y el coeficiente de sustentación del ala que se muestra en la ecuación
3.4.
C Lw = C Low + C Lα , w α w
(3.4)
Usando las ecuaciones 3.3, 3.4 y los criterios de estabilidad, se obtienen el coeficiente
de momento de cabeceo a un ángulo de ataque cero (Cm,ow), y el coeficiente de momento de
cabeceo del ala (Cm,αw), que se muestran en las ecuaciones 3.5 y 3.6.
 X cg X ac 

C m,ow = C m ,acw + C L ow 
−
c
c


(3.5)
 X cg X ac 

C m,αw = C L α ,W 
−
c
c


(3.6)
De las ecuaciones 3.5 y 3.6 se deduce, que para proporcionarle a la aeronave un ángulo
de ataque positivo, el coeficiente de momento de cabeceo debe ser mayor que cero (Cm,o > 0),
y para que el diseño de un ala sola, sea estable, el centro aerodinámico debe encontrarse por
detrás del centro de gravedad, para hacer que el coeficiente de momento sea menor que cero
(Cm,α < 0).
En la mayoría de los casos, el ala de la aeronave tiene un efecto desestabilizante en la
estabilidad longitudinal, que puede ser contrarestada con la contribución del resto de los
componentes (Phillips, 2004).
12
Contribución Ala – Cola
Para una aeronave que posee un empenaje horizontal ubicado detrás del ala, el
diagrama de cuerpo libre se muestra en la figura 3.4.
Figura 3.4: Diagrama de cuerpo libre ala – estabilizador horizontal mostrando la
contribución de la cola al momento de cabeceo.
Como ya fue discutido, la aeronave será estable longitudinalmente si luego de una
perturbación se produce un momento restaurante que devuelva la aeronave a su estado de
equilibrio. La mayor respuesta de contribución a la estabilidad longitudinal la tiene el
empenaje horizontal. De la sumatoria de momentos resultante del diagrama de cuerpo libre se
obtiene la ecuación 3.7.
M t = −lt [Lt cos(α LRF − ε ) + Dt sen(α LRF − ε )]
− z cgt [Dt cos(α LRF − ε ) − Lt sen(α LRF − ε )] + M act
(3.7)
Lo que resulta en las ecuaciones 3.8 y 3.9.
M t = −lt Lt = −lt C Lt
C m ,t =
1
ρU 2t S t
2
Mt
= −VH η t C Lt
Q
(3.8)
(3.9)
Como puede observarse de la ecuación 3.9, el coeficiente de momento de cabeceo del
estabilizador horizontal (Cm,α t) depende del volumen del estabilizador horizontal (VH) y del
13
coeficiente de sustentación del mismo (CLt), así como también del brazo (lt) que produce el
momento alrededor del centro de gravedad.
De la figura 3.4, se observa, que el ángulo de ataque de la cola se verá afectado por la
corriente de flujo de aire que pasa a través del ala, quedando expresado el ángulo de ataque de
la cola como en la ecuación 3.10 y consecuentemente el coeficiente de sustentación del
empenaje horizontal, como lo muestra la ecuación 3.11.
α t = α w − i w − ε + it
(3.10)
C Lt = C Lα t (α w − i w − ε + i )
(3.11)
El ángulo aguas abajo (ε) se expresa como en la ecuación 3.12, y puede ser aproximado
por la teoría de sustentación de ala finita. Suponiendo una distribución de sustentación elíptica
del ala y que el empenaje horizontal se encuentra detrás de esta, el ángulo ε se puede
determinar como lo muestra la ecuación 3.13, derivando la ecuación 3.13 con respecto al
ángulo de ataque se obtiene la ecuación 3.14.
ε = ε0 +
ε=
dε
αw
dα
2C L w
πAR
dε 2C L αw
=
dα
AR
(3.12)
(3.13)
(3.14)
La expresión lineal del coeficiente de momento de cabeceo es mostrada en la ecuación
3.15, de allí, se obtienen el coeficiente de momento de cabeceo del empenaje horizontal para
ángulo de ataque cero, ecuación 3.16, y la variación del coeficiente de momento de cabeceo
del empenaje horizontal en función del ángulo de ataque, ecuación 3.17.
dε 

C m, gt = V H η t C Lα t (ε 0 + i w − it ) − V H η t C Lα t α 1 −

 dα 
(3.15)
14
C m,ot = η tVH C L α t (ε 0 + i w − it )
(3.16)
dε 

C m,αt = −η tV H C L αt 1 −

 dα 
(3.17)
Contribución del Fuselaje
Las fuerzas y momentos aerodinámicos que se producen en el fuselaje son complejos y
se ven afectados por la interacción con el ala y con la cola, para tener una aproximación real,
estos deben ser estudiados con ensayos en el túnel de viento o simulaciones numéricas, sin
embargo debido a que normalmente el fuselaje aporta un momento desestabilizante a la
aeronave, es necesario tener un primer acercamiento al efecto que este produce a la estabilidad
en los diseños preliminares de la aeronave (Phillips, 2004), este puede ser obtenido usando
diversos métodos empíricos y de manual, en esta investigación será usado el método
presentado por Hoak (1960) quien desarrollo experimentalmente la correlación mostrada en la
ecuación 3.18, del coeficiente de momento de cabeceo del fuselaje respecto al centro de
gravedad.
C m, f
df
lf 
=
= −2 1 − 1,76
c
1
cf 
 f
ρU 2 S f c f

2
mcgf




3
2

α
 f

(3.18)
La figura 3.5 muestra la vista en planta del fuselaje de la aeronave con los principales
datos de entrada a la ecuación 3.18. La contribución total del fuselaje a la estabilidad estática
de la aeronave se obtiene de multiplicar la ecuación 3.18 por las características físicas del
(
)
fuselaje y dividirla entre las características físicas del ala S f c f S c , como lo muestra la
ecuación 3.19, que puede ser escrita como en la ecuación 3.20, que a su vez se desglosa en, el
coeficiente de momento de cabeceo del fuselaje para un ángulo de ataque cero (Cm,oƒ),
ecuación 3.21 y en el coeficiente de momento de cabeceo del fuselaje con respecto al ángulo
de ataque, mostrado en la ecuación 3.22.
15
Figura 3.5: Vista en planta y de perfil del fuselaje de un aeroplano.
df
S f l f 
(∆C m ) f = −2
1 − 1,76
c
Sc 
 f





3
2

α
 f

(3.20)
∆C m, f = (∆C m 0 ) f + (∆C m,α ) f α
df
S f l f 
(∆C m ,0 ) f = −2
1 − 1,76
c
Sc 
 f





df
S f l f 
(∆C m ,α ) f = −2
1 − 1,76
c
Sc 
 f

3
2




(3.19)

α
 0f

(3.21)




(3.22)
3
2
Contribución de los Sistemas Propulsores
La estabilidad estática de la aeronave se ve influenciada por los sistemas de propulsión,
este desarrollará una fuerza normal en su plano de rotación que creará un momento de cabeceo
alrededor del centro de gravedad, produciendo una contribución, al coeficiente de momento de
cabeceo respecto al ángulo de ataque.
Esta contribución puede resultar difícil en una primera estimación, debido a los efectos
indirectos que el sistema de propulsión causa sobre las características de la aeronave, por lo
que comúnmente es estimado de modelos propulsados, en el túnel del viento (Nelson 1998).
16
Estabilidad Estática Latero – Direccional
Estabilidad Estática Lateral
La estabilidad estática direccional es provista principalmente por el timón de dirección
de la aeronave, si una aeronave es estable direccionalmente, al producirse cualquier
perturbación lateral, este debe producir un momento de guiñada que tienda a regresar a la
aeronave a su posición original de equilibrio, esto es, que para un ángulo de deslizamiento (β)
positivo, asumido de derecha a izquierda, la aeronave requerirá un momento restaurante (n)
positivo (sentido horario), esto se expresa matemáticamente en la ecuación 3.23.
∂n
>0
∂β
∂C n
≡ C n,β > 0
∂β
(3.23)
La estabilidad de guiñada es determinada principalmente por la contribución del
fuselaje, hélice y cola vertical, el fuselaje y la hélice aportan un efecto desestabilizante, pero
este puede ser contrarrestado con el aporte estabilizante del timón de dirección.
Contribución del empenaje vertical
Cuando una aeronave está volando con un ángulo de deslizamiento positivo, la cola
vertical está a un ángulo de ataque de corriente libre y desarrolla una sustentación, que origina
una fuerza de lateral de derecha a izquierda, si el empenaje vertical de la aeronave está
ubicada detrás del centro de gravedad, esta sustentación producirá un momento positivo de
guiñada alrededor del centro de gravedad, que tenderá a volver a la aeronave en la dirección
del viento relativo retornando el ángulo de deslizamiento a cero.
Por otro lado los vórtices de la punta del ala y la hélice colocada en la nariz del fuselaje
de una aeronave pueden producir un ángulo lateral inducido (εs) en el timón de dirección,
cuando la aeronave esta volando con un ángulo de deslizamiento. Para pequeños ángulos de
deslizamiento, el ángulo lateral inducido en el timón de dirección puede ser considerado como
una función lineal de β, véase ecuación 3.24.
17
(3.24)
ε s = ε so + ε s , β β
Para pequeños ángulos de ataque y de deflexión del timón de dirección, la sustentación
desarrollada en el estabilizador vertical es lineal al ángulo de ataque y al ángulo de deflexión
del timón de dirección, se asumirá la deflexión del timón a la izquierda como positiva, esta
deflexión positiva del timón de dirección producirá un ligero incremento hacia la derecha en la
sustentación del estabilizador vertical y un incremento negativo al momento de guiñada, así la
contribución del estabilizador vertical a la estabilidad de guiñada puede definirse como se
muestra en la ecuación 3.25.
(∆n )v = 1 ρVv S v [lv C L v ,α (β − ε s − ε rδ r ) + cv Cm, v ,δ δ r ]
2
(3.25)
r
Sustituyendo la ecuación 3.24 en la ecuación 3.25 y adimensionalizando se obtiene el
coeficiente de momento de guiñada de la cola vertical, que se muestra en la ecuación 3.26, de
la cual se desglosan el coeficiente de guiñada respecto al ángulo de deslizamiento; mostrado
en la ecuación 3.27 y la contribución que provee la deflexión del timón de dirección a la
derivada de control en guiñada, mostrada en la ecuación 3.28.
(∆C n ) v = η v

 
S v lv 
cv
C Lv ,α (1 − ε s , β ) v β − C Lv ,α ε s 0 −  ε r C Lv ,α − C m v ,δ r δ r 
Sb 
lv

 
(3.26)
S v lv
C Lv ,α (1 − ε s , β ) v
Sb
(3.27)


c
 ε r C Lv ,α − v C m v ,δ r 
lv


(3.28)
(∆C n , β ) v = η v
∆C n ,δ r = η v
S v lv
Sb
Contribución del Fuselaje
La contribución que el fuselaje hace a la estabilidad estática de guiñada produce un
efecto desestabilizante en la aeronave. Para una primera estimación del coeficiente de
momento de guiñada que aporta el fuselaje a la aeronave, se utilizará la correlación
experimental de Hoak (1960), mostrada en la ecuación 3.29.
18
Cn f
df
lf 
≡
= 2 1 − 1,76
c
1 2
cf 
 f
ρu S f c f

2
ncgf




32

β


(3.29)
Al igual que en la aproximación utilizada en la contribución del fuselaje al momento de
cabeceo, la contribución total del fuselaje a la estabilidad estática de guiñada de la aeronave se
obtiene de multiplicar la ecuación 3.29 por las características físicas del fuselaje y dividirla
entre las características físicas del ala (S f c f Sb ) , como lo muestra la ecuación 3.30, que
puede ser rescrita como lo muestra la ecuación 3.31.
(∆C n , β ) f ≡
ncgf
1
ρ u 2 Sb
2
=
Sf cf
Sb
C n f = (∆C n , β ) f β
d
Sflf 
1 − 1,76 f
(∆C n , β ) f = 2
c
Sb 
 f





32




(3.30)
(3.31)
Sustituyendo la ecuación 3.22 en la ecuación 3.31 se obtiene la ecuación 3.32
(C n , β ) f ≅ −(∆C m ,α ) f
c
b
(3.32)
Es importante resaltar que estas ecuaciones muestran una primera aproximación, para
fases preliminares de diseño, y que es necesario hacer un estudio que dé como resultado una
estimación más real, empleando métodos numéricos y ensayos en túnel de viento.
Estabilidad Estática de Banqueo
Una aeronave se dice estable estáticamente en banqueo, cuando la aeronave comienza
un deslizamiento (β) y por el efecto diedro se crea un momento de banqueo (ℓ) restaurante tal
que tiende a disminuir tal deslizamiento. Deslizamiento positivo crea un momento de banqueo
negativo, esto, se traduce matemáticamente a la ecuación 3.33.
19
∂l
≡ C l,β < 0
∂β
(3.33)
El ángulo de banqueo (Φ) es medido con respecto a la orientación que tiene el
aeroplano con la tierra, a diferencia del ángulo de ataque y del ángulo de deslizamiento que
son medidos con respecto a la orientación de la aeronave con respecto al viento relativo. De la
figura 3.6 puede observarse, que una perturbación positiva en el ángulo de banqueo (ala
derecha de la aeronave hacia abajo) resulta en un componente positivo de la velocidad de
deslizamiento, lo cual está definido para proporcionar un ángulo de deslizamiento positivo.
Figura 3.6: Fuerza de desbalance y deslizamiento resultante producido por una perturbación
en banqueo.
La estabilidad de banqueo proporciona a la aeronave una tendencia inherente a
mantener las alas niveladas en vuelo cuando el aeroplano está arreglado para no tener ángulo
de deslizamiento. La estabilidad de banqueo es significantemente afectada por las
interacciones entre el fuselaje, el ala y la cola.
20
Contribución del Diedro del ala
La mayor contribución a la derivada de estabilidad de banqueo la aporta el ángulo de
diedro del ala (Г), definido positivo cuando las puntas del ala se encuentran por encima de la
cuerda en el encastre del ala, como lo muestra la figura 3.7; cuando una aeronave comienza un
deslizamiento, que produce un componente del viento relativo hacia un lado de la aeronave,
esta ala experimentará un incremento en el ángulo de ataque y por consiguiente en la
sustentación, mientras que la otra ala de la aeronave experimenta un efecto opuesto. Estos
efectos en las alas, provocan un momento de banqueo, que pretende devolver el deslizamiento.
Figura 3.7: Contribución del Diedro a la Estabilidad de de Banqueo.
La sustentación adicional creada en el movimiento es el resultado del cambio en el
ángulo de ataque producido por el deslizamiento, que esta directamente relacionado con las
componentes de la velocidad, de esta manera se obtienen las ecuaciones 3.34 y 3.35.
∆α =
vn
u
v n = usenΓ
(3.34)
(3.35)
Una aproximación al ángulo de deslizamiento puede observarse en la ecuación 3.36,
además, si se asume que el ángulo de diedro es pequeño se puede escribir la expresión de
ángulo de ataque en función del ángulo de diedro como lo muestra la ecuación 3.37.
21
β=
υ
u
∆α ≅ β Γ
(3.36)
(3.37)
El aporte del diedro del ala a la estabilidad de banqueo, puede obtenerse según Phillips
(2004), de la ecuación 3.38, donde el radio de la derivada de estabilidad de banqueo, puede ser
obtenido de la ecuación 3.39, también mostrada por Phillips (2004).
(∆C l , β ) Γ w = −
kl = 1+
2Γ
k l C Lw ,α
3π
3π a 2 ∞ 3 sin(nπ 2) a n
+∑
8 a1 n =3 4 − n 2
a1
(3.38)
(3.39)
Contribución del Fuselaje
La contribución del fuselaje a la derivada de estabilidad de banqueo de la aeronave,
depende de la posición vertical del ala con respecto al fuselaje, cuando una aeronave
experimenta deslizamiento las componentes del viento relativo deben fluir como lo muestra la
figura 3.8, en el ángulo de ataque local en las estaciones internas del ala. Para una posición
baja de las alas, el fuselaje contribuye al efecto diedro negativo, causando inestabilidad de
banqueo y para una aeronave con ala alta la interacción ala – fuselaje causa un efecto
estabilizante de diedro positivo, que tiende a volver la nivelación de las alas.
Figura 3.8: Contribución a la Estabilidad de Banqueo de la interacción Ala – Fuselaje.
22
La interacción ala – fuselaje es muy compleja, depende de la geometría y de la
ubicación de ambas, para obtener una aproximación del aporte a la estabilidad es
recomendable el uso de simulaciones numéricas y ensayos en túneles de viento. Sin embrago
como estimación inicial; un ala alta aporta un efecto estabilizante, equivalente alrededor de
dos o tres grados del diedro del ala y el ala baja aporta un efecto desestabilizante, alrededor de
tres o cuatro grados de diedro negativa del ala, mientras que la contribución de un ala media
puede ser despreciada (Phillips, 2004).
Contribución de la Cola
El estabilizador horizontal al igual que el ala contribuye al efecto diedro, sin embargo,
debido a que su tamaño es muy pequeño en comparación con el del ala, su contribución es
muy pequeña, Phillips (2004) estima la contribución del estabilizador horizontal al momento
de banqueo, de la interacción entre los estabilizadores, horizontal y vertical, como lo muestra
la ecuación 3.40.
(∆C l , β ) h = −0,08η v
S v bh
(1 − ε s , β ) v C Lv ,α
Sb
(3.40)
Cuando se produce una fuerza en el estabilizador vertical, esta resulta en un
deslizamiento, si esta fuerza es aplicada por detrás del centro de gravedad, se produce un
momento estabilizante de guiñada y si el centro aerodinámico del estabilizador vertical se
encuentra alineado con el eje de banqueo, esta fuerza puede desencadenar un momento de
banqueo significante que Phillips (2004) describe en las ecuaciones 3.41 y 3.42.
(∆C l ) v = −η v
S v hv
C Lv ,α [(1 − ε s , β ) v β − ε s 0 − ε r δ r ]
Sb
(3.41)
S v hv
(1 − ε s , β ) v C Lv ,α
Sb
(3.42)
(∆C l , β ) v = −η v
23
CAPÍTULO IV
ESTIMACIÓN DE LAS DERIVADAS DE ESTABILIDAD
El método de representación de fuerzas y momentos aerodinámicos como coeficientes
de estabilidad fue introducido por G. H. Bryan, en su publicación en 1911. En esta se asume
que las fuerzas y momentos aerodinámicos pueden ser expresados como función de valores
instantáneos de perturbación de variables. La perturbación de variables se define como
cambios instantáneos en las condiciones de velocidades lineales y angulares, control de
deflexiones y sus derivadas (Nelson, 1998). Asumiendo esto, las fuerzas y momentos
aerodinámicos pueden ser expresados por medio de una expansión de la serie de Taylor, de la
perturbación de variables alrededor de su referencia de condición de equilibrio.
Derivadas de Estabilidad Longitudinal
Longitudinalmente las fuerzas y momentos actuantes en una aeronave son analizados
en función del ángulo de ataque, de la variación instantánea del ángulo de ataque respecto al
tiempo, de la velocidad de rotación longitudinal y de la deflexión del elevador (Nelson, 1998).
La tabla 4.1 muestra las derivadas longitudinales de estabilidad.
Tabla 4.1: Derivadas de estabilidad longitudinal.
Xu =
Zw =
− (C Du + 2C D 0 )QS -1
(s )
mU
− (C L ,α + C Do )QS
(s-1)
Xw =
− (C D α − C Lo )QS
mU
(s-1)
Z α = UZ W& (ft/s2) o (m/s2)
mU
c QS
Z α& = UZ W& (ft/s2) o (m/s2)
(ft/s2) o (m/s2)
Z q = C L ,q
2U m
(QS c )
(QS c )
(1/ft.s) o
M u = C mu
(1/ft.s) o (1/m.s) M w = C m ,α
UI Y
UI Y
(1/m.s)
c QS c -1
(s )
M q = C m ,q
M α = UM w (s-1)
2U I Y
− (C Lu + 2C Lo )QS -1
(s )
mU
c
Z w& = C L,α&
QS (Um)
2U
C L ,δ e QS
Zδ e = −
(ft/s2) o (m/s2)
m
c QS c
(ft-1) o
M w& = C m,α&
2U UI Y
(m-1)
Zu =
M δe = C m,δ e (QSc ) / I Y (s-2)
24
Derivadas de Estabilidad Latero Direccional
El comportamiento latero – direccional de la aeronave en vuelo es analizado en función
del ángulo de deslizamiento, de la velocidad angular de banqueo, de la velocidad angular de
guiñada, de la deflexión de alerones y timón. La tabla 4.2 muestra un resumen de las derivadas
de estabilidad latero – direccionales.
Tabla 4.2: Derivadas de estabilidad latero –direccional.
Yβ =
QSCY , β
m
QSb 2 C n , p
NP =
Lβ =
Yδ a =
(ft/s2) o (m/s2)
-1
(s )
2I ZU
QSbC l , β
IX
QSbC y ,δ a
m
Nδ a =
(s-2)
(s-2)
QSbCY , p
2mU
Lp =
(ft/s) o (m/s)
QSbC n , β
Nβ =
(ft/s2) o (m/s2) Yδ r =
QSbC n ,δ a
IZ
YP =
(s-2)
IZ
QSb 2 C l , p
-1
(s )
2I X U
QSC y ,δ r
Nδ r =
m
QSbC y , r
2mU
Lr =
(s-2)
(ft/s) o (m/s)
QSb 2 C n ,r
Nr =
2I ZU
QSb 2 C l ,r
(ft/s2) o (m/s2) Lδ a =
QSbC n ,δ r
IZ
Yr =
Lδ r =
2I X U
QSbC l.δ a
IX
QSbC l ,δ r
IX
(s-1)
(s-1)
(s-2)
(s-2)
Estimación de los Coeficientes de Estabilidad
En este estudio los coeficientes de estabilidad han sido obtenidos utilizando el código
Tornado basado en el método vortex lattice. La validación de este método para obtener fuerzas
y momentos en el ANCE X-2 se realizó comparando los coeficientes de sustentación,
resistencia, y momento obtenidos por medio de ensayos en túnel de viento, del código PAN
AIR (A502i) y de Digital Datcom. Se decidió utilizar el ANCE X-2 para realizar la validación
debido a que se cuenta con datos experimentales de este, producto de investigaciones previas y
teniendo en cuenta que la única diferencia entre el ANCE X-3 y el X-2, es la pequeña
deformación en la punta del ala, que solo genera una pequeña diferencia entre los coeficientes
aerodinámicos menor al uno por ciento (Boschetti, 2006).
25
Tornado Vortex Lattice
Los coeficientes de estabilidad serán obtenidos haciendo uso del código Tornado
versión T131b. Tornado es un programa de fuente abierta basado en el método vortex lattice
escrito en MATLAB. Este código modela cualquier número de superficies sustentadoras
tridimensionales para computar fuerzas y momentos producto del paso de flujo potencial sobre
estas. Es ampliamente utilizado en diseño conceptual para estimar fuerzas no viscosas así
como cualquier otro método vortex lattice (Melin, 2000a).
El método vortex lattice representa el ala como una superficie plana dividida en
paneles cuadrilaterales sobre los cuales es impuesto un vórtice de herradura. La ley de BiotSavat es utilizada para calcular la velocidad inducida por cada vórtice de herradura en un
punto de control específico. Un grupo de ecuaciones algebraicas lineales representa la
intensidad de cada vórtice al sumar todos los puntos de control, mientras que se satisface la
condición de frontera que indica que el flujo no atraviesa las superficies. La circulación del ala
y la presión diferencial entre la parte inferior y superior del ala son función de la intensidad de
cada vórtice. Finalmente, las fuerzas son obtenidas por integración de la diferencias de presión
(Bertin y Smith, 1998 y Melin, 2000b). En Tornado, el arreglo de vórtice de herradura de otros
códigos de vortex lattice, es reemplazado con un arreglo de vórtice de cabestrillo. Este
funciona de la misma forma, pero las patas de la herradura son flexibles, y posee siete
elementos de igual intensidad (Melin, 2006). Esto trae como ventaja mayor exactitud para
estimar fuerzas y momentos en ángulos de ataque y deslizamiento diferentes de cero, o cuando
se aplican velocidades de rotación.
El código Tornado consta de un preprocesador, un procesador y un post procesador. El
preprocesador consta de tres fases, la entrada; donde el usuario define la forma externa de la
aeronave, el diseñador; donde se diseña la plataforma del ala, esta debe ser localizada en una
coordenada específica, con una geometría predeterminada, ángulo de ataque, envergadura,
diedro y deflexión de las superficies de control, y el mallador que divide el ala en paneles. La
función del procesador es convertir los resultados intermedios del preprocesador en fuerzas y
momentos, para calcular las derivadas de primer orden tornado ejecuta un cálculo central
diferencial usando un estado preseleccionado y perturbando por pequeñas cantidades, los datos
26
de entrada del preprocesador contiene toda la información necesaria para la aproximación
numérica. Por último, el post-procesador presenta los resultados de los cómputos de una
manera comprensible (Melin, 2000a).
Modelo Computacional
El modelo simulado en el código Tornado Vortex Lattice consta de siete superficies
planas sin espesor. Las superficies sustentadoras (ala y estabilizadores) han sido simuladas
como superficies planas con la curvatura correspondiente a los perfiles utilizados en estas
superficies. La geometría está formada por 1.100 puntos de control, el tren de aterrizaje y la
cámara no se encuentran incluidos en esta debido a que la contribución de estos componentes
a las fuerzas no viscosas pueden considerarse despreciables. El fuselaje y los botalones fueron
idealizados como objetos cruciformes, como se muestra en la figura 4.1, esta forma de simular
cuerpos fuselados es altamente eficiente para obtener cargas distribuidas y resistencia inducida
(Miranda, 1977). El centro de gravedad se fijo a 25% de la cuerda media aerodinámica del ala.
Figura 4.1: Rejilla de vórtices del ANCE X-2 utilizado en la simulación con el código
Tornado Vortex Lattice.
El estudio se llevó a cabo a un valor de velocidad fija de 41,18 m/s, que corresponde a
la velocidad de crucero del aeroplano. Las velocidades de la aeronave nunca exceden de Mach
igual a 0,3, por lo que se considera que las fuerzas y momentos obtenidos en flujo no viscoso
deben ser independientes del valor del número de Mach. La simulación fue realizada para
27
ángulos de ataque desde -8 a 12 grados. Cada corrida tomó un tiempo de respuesta de 1 min
con 43 s en un computador personal Pentium 4 de 3,06 GHz con 504 MB de memoria RAM.
Digital Datcom
Datcom es un método analítico – empírico desarrollado por la fuerza aérea de los
Estados Unidos para estimar características de estabilidad y control en aeronaves de ala fija
(Hoak, 1960, Finck, 1978). Este fue condensado en un programa de computación de fuente
abierta escrito en 1979 llamado Digital Datcom en Fortran IV, y adaptado a Fortran 90 en
1999. Datcom requiere como datos de entrada las características geométricas de la aeronave y
sus condiciones de vuelo por medio de una de una serie de variables preestablecidas.
Para una configuración completa del aeroplano (ala, fuselaje y estabilizadores
horizontal y vertical) el programa requiere como valores de entrada los datos geométricos de
este. Si se tienen datos experimentales de los componentes por separado, pueden ser utilizados
como datos de entrada para la obtención de algunas de las características aerodinámicas en
estudios bajo régimen subsónico. Digital Datcom entregará como resultado los coeficientes de
fuerzas y momentos, y las derivadas de estabilidad de todo el aeroplano. Solo para aeronaves
con ala recta rectangular los efectos de potencia y los efectos suelo son incluidos en los
resultados de estabilidad longitudinal (Williams y Vukelich, 1979).
PAN AIR
PAN AIR (A502) es un software de fuente abierta basado en el método de los paneles,
que permite resolver el campo de velocidades y presiones alrededor de cuerpos arbitrarios
inmersos en flujo potencial subsónico o supersónico, aplicando la ecuación de Laplace y la
corrección de Prandtl – Glauert. Este software puede ser utilizado para estudios bajo
regímenes subsónicos (M<0,6) y supersónicos (M>1), pero no en régimen transónico, donde
los efectos viscosos son dominantemente considerables (Derbyshire y Sidwell, 1982).
El método de los paneles distribuye en un gran número de paneles cuadrilaterales
elementales las incógnitas sobre la superficie del contorno del cuerpo. Cada uno de estos
paneles contiene uno o más tipos de singularidades, que pueden ser vórtices fuentes o
28
dobletes. Estas singularidades son determinadas especificando alguna variación funcional a
través del panel (constante, lineal o cuadrática) fijando el valor de estas para los parámetros de
intensidad correspondiente. La intensidad es determinada resolviendo la ecuación de frontera
adecuada, para luego computar el campo de presiones y el campo de velocidades (Bertin y
Smith, 1998)
Modelo Computacional
El modelo simulado en este código representa solo la mitad simétrica del aeroplano y
fue creado en formato LaWGS (Craidon, 1985) compatible con PAN AIR. La geometría
utilizada para la simulación consta de 4.126 paneles distribuidos en 27 mallas; 22 definidas
como indirectamente impermeables (para modelar superficies sustentadoras), 4 como
directamente impermeables (para modelar superficies no sustentadoras), y una con condición
de superficie de base. Además existen 17 mallas que forman las ondas necesarias para
imponer la condición de Kutta de vorticidad cero en bordes de fuga y bases de cuerpos
fuselados. El tren de aterrizaje y la cámara no fueron considerados debido a que su
contribución es despreciable en estudios con flujo no viscoso (Boschetti, et al, 2008a). Las
figuras 4.2 y 4.3 muestran la geometría de los paneles del ANCE X-2 utilizada en la
simulación con el código PAN AIR.
El modelo de los paneles del ANCE fue ensayado utilizando la versión A502i de PAN
AIR (Saaris, 1992). El estudio se realizó a un número fijo de Mach igual a 0,15, representativo
de las condiciones de vuelo subsónico incompresible del ANCE, el ángulo de ataque se varió
de -10 a 12 grados, manteniendo la onda rígida, para cada variación del ángulo de ataque. El
tiempo de espera en un computador personal Pentium 4 de 3,6 GHz con 504 MB de memoria
RAM fue de 7 min con 23 s.
El coeficiente de sustentación y el coeficiente de momento fueron obtenidos por medio
de la integración numérica de los coeficientes de presión de segundo orden (Saaris, 1992). El
coeficiente de resistencia debida a la sustentación o del vórtice se computó por medio de la
variación de los coeficientes de presión en el plano de Trefftz.
29
Figura 4.2: Geometría de los paneles del ANCE X-2 utilizado en la simulación con el código
PAN AIR sin las ondas.
Figura 4.3: Geometría de los paneles del ANCE X-2 utilizado en la simulación con el código
PAN AIR mostrando las ondas.
30
Estudios Experimentales en el Túnel de Viento
Los experimentos se llevaron a cabo empleando un túnel de viento modelo Rollab
SWT-009, no presurizado, de ciclo cerrado y garganta cerrada, que posee una sección de
pruebas cuadrada de 0,32 m × 0,32 m, de paredes transparentes, ubicado dentro de las
instalaciones del laboratorio de aerodinámica de la Universidad Nacional Experimental
Politécnica de la Fuerza Armada, núcleo Maracay, Venezuela, a 407,8 m sobre el nivel del
mar. Para los experimentos se construyó un modelo a escala en fibra de vidrio reforzado con
resina de poliéster, pintado en negro brillante a escala 1:20,2 basados en los planos del ANCE
X-2. El túnel fue calibrado antes de cada corrida con el fin de garantizar la correcta escala de
la balanza y de la sonda pitot, obtener el ángulo de alineamiento aerodinámico de la balanza y
el factor de turbulencia del túnel (Boschetti, 2006).
El modelo se probó de forma invertida (debido a un requerimiento de la balanza)
sujetado por la extensión del soporte que se une al modelo en un solo punto que esta alineado
con su centro de gravedad.
El modelo a escala del ANCE X-2 se ensayó a nueve velocidades diferentes, para
obtener el valor de sus coeficientes aerodinámicos en función del número de Reynolds.
Durante cada ensayo el ángulo de ataque fue variado, de forma creciente y decreciente,
teniendo así dos mediciones para cada condición. El modelo se probó a -8 a 16 grados de
ángulo de ataque (Boschetti, 2006).
Los valores obtenidos en estos ensayos de número de Reynolds fueron multiplicados
por el factor de turbulencia, y los efectos de bloqueo, capa límite y retardo de la balanza
fueron corregidos (Boschetti, 2006). El modelo ensayado en el túnel de viento alcanzó el
régimen turbulento, de esta manera pudieron ser aplicadas correcciones de efectos de escala a
estos valores para obtener la curva de resistencia polar del aeroplano en vuelo de crucero
(Re=1,413x106) (Boschetti, et al, 2006).
31
Validación
La figura 4.4 muestra las gráficas de coeficiente de sustentación en función del ángulo
de ataque del ANCE X-2 empleando los diferentes métodos. Esta figura muestra una buena
correlación entre los valores de coeficientes de sustentación en función del ángulo de ataque
obtenidos con Tornado y Digital Datcom, y una excelente correlación de los valores de
coeficientes de sustentación obtenidos mediante el uso de PAN AIR respecto a los resultados
experimentales.
Figura 4.4: Curvas del coeficiente de sustentación en función del ángulo de ataque del ANCE
X-2 obtenidas con Tornado, Digital Datcom, PAN AIR y ensayos en túnel del viento.
La tabla 4.3 muestra la comparación de la pendiente de la curva de sustentación, el
coeficiente de sustentación para ángulo de ataque cero y el coeficiente de sustentación
máximo, obtenidos de ensayos en túnel de viento, Tornado, Digital Datcom y PAN AIR del
modelo ANCE X-2. En la tabla 4.3 se observa que Tornado tiene una correlación con los datos
experimentales de 75,1% para la pendiente de la curva de sustentación y de 92% para ángulo
de ataque cero, Digital Datcom muestra una correlación de 73,5% para la pendiente de la
curva de sustentación, de 91% para ángulo de ataque cero y 80,19% para coeficiente de
32
sustentación máximo. PAN AIR muestra excelente correlación con los valores obtenidos de
ensayos en túnel de viento. Los códigos Tornado y PAN AIR no muestran la entrada en
pérdida debido a que estos códigos solo calculan el campo de flujo potencial siendo imposible
estimar los efectos viscosos, como lo es el desprendimiento de capa límite causa del fenómeno
de entrada en pérdida.
Tabla 4.3: Comparación de los parámetros de la curva de sustentación del modelo ANCE X-2
obtenidos por los diferentes métodos.
Túnel de viento
Tornado
Datcom
PAN AIR
C Lα
0,074
0,092
0,094
0,074
C Lo
0,474
0,511
0,518
0,474
C L MAX
1,424
-
1,142
-
Las figuras 4.5 y 4.6 muestran la curva de resistencia polar, y la pendiente del
coeficiente de resistencia en función del coeficiente de sustentación al cuadrado del ANCE
X-2, respectivamente, estimada con Tornado, en comparación con las obtenidas de Digital
Datcom, PAN AIR y ensayos en túnel del viento. Debido a que Tornado y PAN AIR solo
computan el campo de flujo potencial no es posible obtener a través de estos la contribución
de la viscosidad a la resistencia. Por este motivo, el coeficiente de resistencia parasita debido a
efectos viscosos subsónicos le fue adicionado a la resistencia inducida para obtener el
coeficiente de resistencia total. El coeficiente de resistencia parasita se obtuvo por medio de
un método que combina razonamientos analíticos y datos empíricos, mostrado por Boschetti,
(2006) y Boschetti, et al, (2008b).
La figura 4.5 muestra una buena correlación entre la curva de resistencia polar obtenida
de Tornado, en comparación con la experimental, para valores de coeficiente de sustentación
entre 0,1 y 0,9, los resultados obtenidos de PAN AIR muestran una excelente correlación con
la curva polar obtenida de ensayo en túnel de viento. La curva de resistencia polar obtenida de
Digital Datcom se mantiene adelantada, debido a que este calcula por si solo la resistencia
viscosa del aeroplano, pero sin modelar el tren de aterrizaje ni la cámara, lo que le resta la
resistencia de estos componentes.
33
La tabla 4.4 muestra la comparación del coeficiente de resistencia mínimo y del
coeficiente de eficiencia de Oswald obtenidos de ensayos en túnel de viento, Tornado, Digital
Datcom y PAN AIR del modelo ANCE X-2. En la tabla 4.4 se observa que Tornado tiene una
correlación con los datos experimentales de 66,9% para el coeficiente de eficiencia de Oswald,
Digital Datcom muestra una correlación de 83,7% del coeficiente de resistencia mínimo y
63,7% para el coeficiente Oswald. PAN AIR muestra excelente correlación con los valores
obtenidos de ensayos en túnel de viento.
Figura 4.5: Curvas del coeficiente de sustentación en función del coeficiente de resistencia del
ANCE X-2 obtenidas con Tornado, Digital Datcom, PAN AIR y ensayos en túnel del viento.
La figura 4.7 muestra la curva del coeficiente de momento en función del ángulo de
ataque del ANCE X-2 obtenida haciendo uso del Tornado, Digital Datcom y PAN AIR. En los
ensayos en el túnel de viento realizados por Boschetti (2006) no se obtuvieron valores de
coeficiente de momento, por lo que se emplearan como parámetros de validación los valores
de coeficiente de momento obtenidos con PAN AIR. Este código es bastante confiable para
obtener este tipo de datos en regímenes subsónicos y supersónicos como lo demostró Madson
y Ericsson (1990). En base a lo antes expuesto, en la figura 4.7 se observa una buena
34
correlación con los valores obtenidos de Tornado y Datcom para ángulos de ataque entre -8 y
2 grados al ser comparados con los de PAN AIR.
Figura 4.6: Pendientes del coeficiente de resistencia en función del coeficiente de
sustentación al cuadrado del ANCE X-2 obtenidas con Tornado, Digital Datcom, PAN AIR y
ensayos en túnel del viento.
Tabla 4.4: Comparación de los parámetros de la curva polar y de la curva de coeficiente de
resistencia en función del coeficiente de sustentación al cuadrado, del modelo ANCE X-2,
obtenidos de los diferentes métodos.
C Do
e
Túnel de viento
Tornado VLM
Datcom
PAN AIR
0,0264
0,7369
0,0285
0,9806
0,0221
1,0045
0,0275
0,7534
35
Figura 4.7: Curvas del coeficiente de momento en función del ángulo de ataque del ANCE
X-2, obtenidos con los códigos Tornado, Digital Datcom y PAN AIR.
Metodología para Estimar las Derivadas de Estabilidad
Luego de simular el modelo computacional en Tornado del ANCE X-2 y obtener una
buena correlación en los rangos de operación de la aeronave, ha sido evaluado en Tornado el
ANCE X-3. Para este modelo han sido simuladas dos configuraciones, la primera con bisagra
de deflexión del elevador y timón de dirección al 50% de la cuerda media de la cola, a la que
se denominó ANCE X-3b, y la segunda a 37,2% denominada versión X-3c. La figura 4.8
muestra el modelado del ANCE X-3 utilizado en la simulación con el código Tornado Vortex
Lattice.
36
Figura 4.8: Rejilla de vórtices del ANCE X–3 utilizado en la simulación con el código
Tornado.
Las simulaciones en Tornado han sido realizadas tomando como variables
independientes; el ángulo de ataque, el ángulo de deslizamiento, las deflexiones en el
elevador, timón de dirección y alerones, y las velocidades angulares alrededor de cada uno de
los ejes de movimiento de la aeronave. La tabla 4.5 muestra el control de variables utilizado en
el estudio. Se fijaron como variables dependientes en este estudio los coeficientes de
sustentación, resistencia y momento en cada uno de los ejes de movimiento del aeroplano.
Tabla 4.5: Control de las variables de estudio.
α
-8° a 12°
-8° a 12°
-8° a 12°
-8° a 12°
-8° a 12°
0
0
0
β
0
0
0
0
0
-5° a 5°
0
0
δe
0
-5
-10
5
10
0
0
0
δa
δr
0
0
0
0
0
0
0
0
0
0
0
0
-20° a 20°
0
0
-20° a 20°
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
p
0
0
0
0
0
0
0
0
60°/s a
-60°/s
q
0
0
0
0
0
0
0
0
r
0
0
0
0
0
0
0
0
0
0
0
60°/s a
-60°/s
0
0
0
60°/s a
-60°/s
37
Resultados de los Coeficientes de Estabilidad
Por medio de las simulaciones efectuadas en Tornado para ambas configuraciones, han
sido obtenidos los valores de coeficientes de fuerza lateral, de sustentación y de resistencia
inducida, así como los coeficientes de momento de guiñada, cabeceo y de banqueo.
Graficando los valores obtenidos para cada una de las simulaciones realizadas, con
ambas configuraciones y usando líneas de tendencia para obtener las derivadas de estas
curvas, han sido obtenidos los coeficientes de estabilidad estáticos de la aeronave. De igual
forma el estudio fue realizado utilizando Digital Datcom en la configuración X-3, la
comparación de los coeficientes obtenidos pueden ser observados en la tabla 4.6.
Los resultados obtenidos de los coeficientes de estabilidad haciendo uso de Tornado
para ambas configuraciones X-3b y X-3c son aproximados, como puede observarse en la tabla
4.6, sin embargo los coeficientes de momento de cabeceo y guiñada respecto a la deflexión de
las superficies de control muestran una ligera disminución del valor para la configuración
X-3c, lo que indica que esta versión permite maniobrar la aeronave de manera más dócil.
Puede observarse también que los resultados obtenidos entre Datcom y Tornado
muestran una correlación de buena a excelente de las derivadas de estabilidad longitudinales
adimensionales con respecto al ángulo de ataque, y una correlación pobre para variaciones de
velocidades de rotación, aunque la pendiente de la derivada mantiene la misma orientación.
En el estudio latero – direccional se aprecia una correlación pobre de las derivadas de
estabilidad estática entre Digital Datcom y Tornado, que puede ser motivada a la
configuración poco convencional del ANCE, teniendo en cuenta que la base de datos de
Digital Datcom ha sido complementada en su mayoría por aeroplanos de configuración
convencional; haciendo que la extrapolación de este método no describa un comportamiento
latero – direccional preciso (Cárdenas, et al, 2008, Melin, 2006).
38
Tabla 4.6: Coeficientes de estabilidad de la aeronave.
CL,α
Tornado
ANCE X-3b
0,0953
Tornado
ANCE X-3c
0,0953
Digital
Datcom
0,0987
CL,q
0,321654
0,321684
0,1479
CL,δe
0,0145
0,0119
-
CL,ά
-
-
0,04074
Cm,α
-0,0475
-0,0476
-0,033
Cm,q
-0,78805
-0,78813
-0,4551
Cm,δe
-0,0608
-0,05
-
Cm,ά
-
-
-0,1754
CD,α
0,003722
0,003722
CY,β
-0,0097
-0,0097
-0,01183
CY,p
0,001311
0,001311
0,00056
CY,r
-0,01124
-0,01124
-
CY,δr
-0,0054
-0,0047
-
CY,δa
-0,00002
-0,00002
-
Cℓ,β
0,0003
0,0003
0,00099
Cℓ,p
-0,01311
-0,01311
-0,00896
Cℓ,r
-0,00375
-0,00375
-0,00245
Cℓ,δr
0,0001
0,0001
-
Cℓ,δa
0,0036
0,0036
-
Cn,β
-0,0027
-0,0027
-0,00125
Cn,p
-0,00056
-0,00056
-0,00084
Cn,r
-0,00749
-0,00749
-0,00413
Cn,δr
-0,003
-0,0026
-
Cn,δa
-0,0003
-0,0003
-
Cmu
0
0
0
CLu
0
0
0
Relación
39
CAPÍTULO V
ESTABILIDAD DINÁMICA DE UNA AERONAVE
La estabilidad dinámica estudia el comportamiento de la aeronave en función del
tiempo (Nelson, 1998). Una aeronave se dice estable dinámicamente si la amplitud de un
movimiento oscilatorio inducido por una perturbación, decrece paulatinamente a un cero
relativo en condiciones de vuelo en equilibrio; si la amplitud del movimiento oscilatorio
inducido tiende a incrementar con el tiempo la aeronave se dice inestable dinámicamente
(Foster, 2005). La figura 5.1 muestra una representación gráfica de estabilidad e inestabilidad
dinámica.
Figura 5.1: Representación gráfica de Estabilidad e Inestabilidad Dinámica.
La respuesta dinámica de una aeronave envuelve un gran número de grados de libertad,
en vuelo esta posee tres grados de libertad en translación, tres rotacionales y un gran número
de grados de libertad en su comportamiento elástico. Este estudio asumirá a la aeronave como
un cuerpo rígido, y será modelado por ecuaciones no homogéneas diferenciales lineales de
segundo orden con coeficientes constantes, que describen las ecuaciones de vuelo de la
aeronave. Estas ecuaciones serán desacopladas en el comportamiento longitudinal y latero –
40
direccional de la aeronave con tres grados de libertad cada una, y serán analizadas para
pequeñas variaciones de su estado de equilibrio.
Estabilidad Dinámica Longitudinal
El movimiento longitudinal comprende dos grados de libertad en translación (axial y
normal) y un grado de libertad en rotación (cabeceo), lo que se traduce en tres grados de
libertad y seis autovalores, los autovalores asociados a este movimiento comprenden dos pares
complejos correspondientes a dos modos oscilatorios, uno ligeramente amortiguado llamado
período largo, y otro pesadamente amortiguado denominado período corto, los dos autovalores
restantes corresponden a los modos de desplazamiento, por lo que son siempre cero.
Movimiento Puramente de Cabeceo
Este estudio considerará que el centro de gravedad de la aeronave se encuentra
restringido a moverse a lo largo de una línea recta a velocidad constante, la aeronave es libre
para realizar movimiento de cabeceo alrededor de su centro de gravedad, tal como se muestra
en la figura 5.2.
Figura 5.2: Modelo Restringido a Movimiento Puramente de Cabeceo.
Siguiendo estas consideraciones la ecuación que representa este movimiento es la
mostrada en la ecuación 5.1. Si el momento y el ángulo de cabeceo son expresados en
41
términos de valores de referencia inicial y luego de sufrir una perturbación, pueden definirse
como en las ecuaciones 5.2 y 5.3.
∑ Momentos de cabeceo =∑ M
cg
= I yθ&&
(5.1)
M = M 0 + ∆M
(5.2)
θ = θ 0 + ∆θ
(5.3)
Si el momento inicial es nulo, la variación de momento se expresa en la ecuación 5.4.
∆M = I y ∆θ&&
(5.4)
Para las restricciones de movimiento, las variables que influyen en este estudio son, el
ángulo de ataque, el ángulo de cabeceo, la velocidad de cabeceo y el ángulo del elevador, esto
representado en una serie de Taylor es mostrado en la ecuación 5.5.
∆M =
∂M
∂M
∂M
∂M
∆α +
∆α& +
∆q +
∆δ e
∂α
∂α&
∂q
∂δ e
(5.5)
Si el cuerpo es alineado de tal manera que coincidan a un tiempo cero las variaciones
en el ángulo de ataque y de cabeceo, ecuación 5.6, igualando la variación de momentos
expresada en las ecuaciones 5.4 y 5.5, se obtiene la ecuación diferencial de segundo orden no
homogénea con coeficientes constantes 5.7, cuya ecuación característica es definida en la
ecuación 5.8.
∆α = ∆θ
y
∆θ& = ∆q = ∆α&
(5.6)
∆α&& − ( M q + M α& )∆α& − M α ∆α = M δ e ∆δ e
(5.7)
λ2 − ( M q + M α& )λ − M α = 0
(5.8)
42
Si la ecuación 5.8 es comparada con la ecuación 5.9, ecuación estándar de segundo
orden resultante de un sistema mecánico compuesto por masa, resorte y un mecanismo de
amortiguamiento mostrado en la figura 5.3.
Figura 5.3: Sistema mecánico de amortiguación.
λ2 − 2ζω n λ + ω n 2 = 0
(5.9)
Entonces la relación de amortiguamiento (ζ) y la frecuencia natural no amortiguada
(ωn) pueden ser descritas por las ecuaciones 5.10 y 5.11
ωn = − M α
ζ =
− ( M q + M α& )
2 − Mα
(5.10)
(5.11)
Resolviendo la ecuación característica del sistema mecánico, ecuación 5.9, se obtienen
las raíces, como se observa en las ecuaciones 5.12 y 5.13
λ1, 2 = −ζω n ± iω n 1 − ζ 2
(5.12)
λ1, 2 = η ± iω
(5.13)
Las raíces de la ecuación característica muestran la respuesta que tendrá la aeronave. Si
las raíces son reales, la respuesta de la aeronave será divergente si el signo es positivo o
amortiguada si es de signo negativo.
43
Si las raíces son complejas, el movimiento respuesta será una oscilación sinusoidal
amortiguada o no amortiguada. El período de la oscilación es descrito por la parte imaginaria
de la raíz y se muestra en la ecuación 5.14.
T=
2π
(5.14)
ω
La velocidad angular de crecimiento o decrecimiento de la oscilación es determinada
por el signo de la parte real, un signo positivo corresponde a un decrecimiento de la oscilación,
mientras el signo negativo corresponde a un aumento. Una medida de la tasa de crecimiento o
decrecimiento de la oscilación, es proporcionada por el tiempo y el número de ciclos, para
doblar, o llevar a la mitad, la amplitud inicial de la perturbación, véase ecuaciones 5.15 y 5.16.
t1 2 o t 2 =
ln(0,5)
η
N 1 2 o N 2 = 0,110
ω
η
(5.15)
(5.16)
Movimiento Longitudinal con Mando Fijo
El movimiento longitudinal de una aeronave con mando fijo luego de una variación en
su estado de vuelo de equilibrio responde a dos modos de movimiento oscilatorios, uno de
ellos es ligeramente amortiguado, llamado modo de largo período y otro pesadamente
amortiguado denominado de período corto.
La ecuaciones 5.17, 5.18 y 5.19 fueron desarrolladas por Nelson (1998) y representan
el comportamiento longitudinal de una aeronave rígida, en ecuaciones diferenciales lineales
ordinarias de segundo orden.
d

 − X u ∆u − X w ∆w + ( g cos θ )∆θ = X δ e ∆δ e + X δ T ∆δ T
 dt

(5.17)
44
d
d




− Z u ∆u + (1 − Z w& ) − Z w  ∆w − (U + Z q ) − gsenθ 0  ∆θ = Z δ e ∆δ e + Z δ T ∆δ T (5.18)
dt
dt




 d2
d
d


− M u ∆u −  M w&
+ M w ∆w +  2 − M q ∆θ = M δ e ∆δ e + M δT ∆δ T
dt
dt 


 dt
(5.19)
Las derivadas de estabilidad Zq y Z ω& contribuyen muy poco a la respuesta de la
aeronave, por lo que son despreciadas, entonces asumiendo esto y reescribiendo las ecuaciones
5.17, 5.18 y 5.19 de la forma mostrada en la ecuación 5.20, se obtiene 5.21.
(5.20)
x& = Ax + Bη
Xu
 ∆u&  
∆w&  
Zu
 =
 ∆q&   M u + M w& Z u
 & 
0
∆θ  
X δe


Z δe
+
 M δe + M w& Z δe M δ T

0

Xw
Zw
M w + M w& Z W
0
0
U
M q + M w& U
1

 ∆δ
 e 
+ M w& Z δ T  ∆δ T 

0

XδT
Zδ T
− g   ∆u 
0  ∆w
0   ∆q 
 
0  ∆θ 
(5.21)
Comparando 5.21 con 5.20, se obtienen las matrices x, η, A y B tal como se muestra en
las ecuaciones 5.22 y 5.23.
 ∆u& 
∆w& 
 ∆δ 
x =  , η =  e 
 ∆q& 
∆δ T 
 &
∆θ 
(5.22)
45
Xu
Xw


Zu
Zw
A=
 M u + M w& Z u M w + M w& Z W M q

0
0

X δe
XδT




Z δe
Zδ T

B=
 M δe + M w& Z δe M δ T + M w& Z δ T 


0
0


0
U
+ M w& U
1
− g
0 
0 

0 
(5.23)
Las raíces características o autovalores del sistema pueden ser obtenidos según la
ecuación.
λ j I − A Pij = 0
(5.24)
Las características de la repuesta a la perturbación se expresan en función de la tasa de
amortiguamiento, la frecuencia natural amortiguada, la relación de amortiguamiento y la
frecuencia natural no amortiguada para el modo longitudinal que se muestran en las
ecuaciones 5.25, 5.26, 5.27 y 5.28.
σ = − real (λ )
2U
c
(5.25)
ω d = imag (λ )
2U
c
(5.26)
ζ =−
λ1 + λ2
2 λ1λ 2
ω n = λ1λ2
2U
c
(5.27)
(5.28)
46
Aproximaciones Longitudinales
Aproximación al Modo de Período Largo
El modo de período largo puede ser considerado como un intercambio gradual de
energía cinética y energía potencial alrededor de una altitud de equilibrio, este modo se
caracteriza por cambios en la altitud y velocidad a ángulos de ataque relativamente constantes,
como lo muestra la figura 5.4.
Figura 5.4: Modo de Período Largo.
Una aproximación al modo de período largo se obtiene despreciando el momento de
cabeceo y considerando que el ángulo de ataque no varía, teniendo en cuenta estas
consideraciones, el modo de período largo queda representado por la ecuación 5.29.
X
 ∆u&   u
∆θ& = − Z u
   U
− g  ∆u
  
0  ∆θ 

(5.29)
Los autovalores de la ecuación 5.29 son obtenidos de las raíces de la ecuación
característica expresada en la ecuación 5.30.
λ1, 2 = −ς p ω n p ± iω n p 1 − ς 2p
(5.30)
47
La frecuencia natural no amortiguada y el radio de amortiguamiento se expresa como
lo indican las ecuaciones 5.31 y 5.32 respectivamente.
− Zu g
U
(5.31)
− Xu
2ω np
(5.32)
ω np =
ζ np =
Aproximación al Modo de Período Corto
Una aproximación al modo de período corto se obtiene al asumir que la velocidad no
varía, como lo muestra la figura 5.5. Teniendo en cuenta esta consideración, la aproximación
al movimiento oscilatorio de período corto queda expresada por la ecuación 5.33.
Z

− u
∆α&  
U
 ∆q&  = 
   M α + M α& Z α
U


 ∆α 
⋅ 
M q + M α&   ∆q 

1
(5.33)
Figura 5.5: Movimiento Oscilatorio de Período Corto.
Resolviendo la ecuación característica de este movimiento oscilatorio, ecuación 5.33,
la frecuencia natural no amortiguada y el radio de amortiguamiento se expresan como lo
indican las ecuaciones 5.34 y 5.35 respectivamente.
48


Z
(5.34)
ω nsp =  M q α − M α 
U


M q + M α& +
ζ nsp =
Zα
U
(5.35)
2ω nps
Estabilidad Dinámica Latero – Direccional
El movimiento lateral de un cuerpo rígido posee tres grados de libertad (deslizamiento,
banqueo y guiñada) y es caracterizada por seis autovalores. Las ecuaciones latero –
direccionales de movimiento surgen de la interacción de fuerzas laterales, momentos de
banqueo y momentos de guiñada, según Nelson (1998), esta interacción puede ser
representada por la ecuación 5.36.
Y
 ∆β&   β
  U
 ∆p&  =  Lβ
 ∆r&  
 &  N β
∆Φ 
 0
U
Lp
 Y 
− 1 − r 
 U
Lr
Np
Nr
1
0
Yp
g cos θ 0  ∆β

    0
U   

∆p
0  ⋅   +  Lδ a
 ∆r 
0    Nδ a
 ∆Φ 
0     0
Yδ r 

U  ∆δ
Lδ r  ⋅  a 
 ∆δ 
Nδ r   r 

0 
(5.36)
Las raíces de las ecuaciones características latero – direccionales, consisten en dos
raíces reales, un par de raíces complejas y dos raíces idénticas iguales a cero. El análisis de
estas raíces indican la respuesta de la aeronave ante una serie de movimientos; lentamente
convergente o divergente, llamado modo de espiral; altamente convergente; denominado
modo de banqueo y un movimiento oscilatorio ligeramente amortiguado con baja frecuencia
llamado banqueo holandés.
Las raíces reales diferentes de cero resultantes de la ecuación característica expresan el
comportamiento en modo de banqueo y en modo espiral, con estos pueden ser obtenidos; la
tasa de amortiguamiento para cada uno de estos modos y con esta el tiempo para amortiguar al
99% de la amplitud, como se expresa en la ecuación 5.37.
49
99% tiempo de amortiguamiento =
ln(0,01)
−σ
(5.37)
Los autovalores para los modos de banqueo y espiral forman un par matemático, para
este par banqueo – espiral, la frecuencia natural no amortiguada y la relación de
amortiguamiento se expresan como en las ecuaciones 5.38 y 5.39.
2U
b
(5.38)
λ1 + λ2
2 λ1λ1
(5.39)
ω n = λ1λ1
ζn = −
El par de raíces complejas describe un movimiento oscilatorio amortiguado, el modo
de banqueo holandés es una combinación fuera de fase de deslizamiento, banqueo y guiñada,
de la misma manera, los autovalores tres y cuatro obtenidos de la ecuación 5.36, permitirán
obtener, la tasa y la relación de amortiguamiento y las frecuencias naturales amortiguada y no
amortiguada de este modo.
Aproximación al Movimiento Espiral
El modo de espiral es caracterizado principalmente por cambios en el ángulo de
guiñada y en la dirección del recorrido, este modo es además lentamente convergente o
divergente. El cambio en el ángulo de guiñada de la aeronave ocurre lentamente con muy poco
deslizamiento. El banqueo y la guiñada permanecen muy bajas durante el movimiento de
espiral. Un modo espiral ligeramente divergente es aceptable previendo que el tiempo
necesario para doblar la amplitud no es pequeño, el resultado de un movimiento en espiral
divergente no controlado se muestra en la figura 5.6, cuando una aeronave en modo de espiral
divergente es perturbada lateralmente de su estado de vuelo de arreglo, esta comenzará una
lenta espiral en dirección de la perturbación, de no ser corregida esta espiral continuará
estrechándose gradualmente.
50
La aproximación al movimiento de espiral se obtiene usualmente despreciando el
producto de la inercia, la velocidad angular de banqueo, el ángulo de banqueo y las ecuaciones
de momento causadas por el deslizamiento (Nelson, 1998), el resultado de esta aproximación
se muestra en la ecuación 5.40. Otra aproximación es obtenida, manteniendo la ecuación de
momento debido al deslizamiento e incluyendo los efectos de la velocidad angular de banqueo
y del ángulo de banqueo, son despreciadas las aceleraciones, las derivadas laterales respecto al
ángulo de deslizamiento y la velocidad angular de guiñada (Phillips, 2004), matemáticamente
se observa en la ecuación 5.41. Foster (2005) aproxima el modo de espiral, manteniendo como
contribuciones más significantes, las del ángulo de deslizamiento y el ángulo de banqueo,
además simplifica la ecuación de acople latero direccional, ignorando la ecuación de fuerza
lateral así como también los términos asociados con el ángulo de banqueo, ecuación 5.42.
λ Espiral =
λ Espiral = −
gb
2U 2
λ Espiral =
L β N r − Lr N β
(5.40)
Lβ
 C l , β C n, r − C l ,r C n , β

C C −C C
l , p n,β
 l ,β n , p
L β N r − Lr N β
− ( Lβ + N β I Y I X )




(5.41)
(5.42)
En este estudio será utilizada la aproximación recomendada por Phillips (2004) puesto
que es la aproximación más consistente con la realidad.
La relación de amortiguamiento de este modo puede ser aproximada como se muestra
en la ecuación 5.43.
σs ≅
2U
λs
b
(5.43)
51
Figura 5.6: Movimientos de Divergencia espiral y Divergencia Direccional.
Aproximación al Banqueo
La respuesta común de una aeronave al paso de cambio en la deflexión del alerón
puede ser observada en la figura 5.7, en la figura se observa que luego de aplicar una deflexión
en el alerón el ángulo de banqueo incrementa linealmente con el tiempo y la tasa de banqueo
aproxima a un valor constante Phillips (2004). El tiempo requerido por el movimiento de
banqueo para aproximar una velocidad angular de banqueo constante es determinado por el
autovalor de banqueo.
Figura 5.7: Respuesta de banqueo al efectuar una deflexión en los alerones.
El tiempo constante en el modo de banqueo, puede ser aproximado asumiendo que el
ángulo de banqueo, es el único grado de libertad importante (Foster, 2005), esto lleva a la
ecuación 5.44.
52
λGIRO ≅ L p
(5.44)
La tasa de amortiguamiento en modo de banqueo se expresa como en la ecuación 5.45.
σr = −
2U
Lp
b
(5.45)
La magnitud del amortiguamiento de banqueo depende del tamaño del ala y de las
superficies de la cola.
Aproximación al Banqueo Holandés
El banqueo Holandés es un movimiento oscilatorio caracterizado por la combinación
de deslizamiento, banqueo y guiñada, tal como se observa en la figura 5.8. El modo de
banqueo holandés puede ser muy molesto para pasajeros y piloto, el componente de guiñada
en este modo es grande, por lo que en algunas ocasiones puede sentirse la impresión que la
cola quiere pasar la nariz de la aeronave.
Figura 5.8: Movimiento Banqueo Holandés.
53
La aproximación usual al movimiento oscilatorio, banqueo holandés, se obtiene
asumiendo que el movimiento consiste solo de deslizamiento y guiñada, esto se expresa en la
ecuación 5.46.
Y
∆β&   β
 =U
 ∆r&   N β

 Y
− 1 − r
 U
Nr
 ∆β
  
 ⋅  ∆r 
  
(5.46)
De la ecuación 5.46, la ecuación característica del modo de banqueo holandés se
expresa como se muestra en la ecuación 5.47.
 Yβ + UN r
U

λ2 − 
Y N − N β Yr + UN β

λ + β r
U

(5.47)
De esta expresión, la frecuencia natural no amortiguada y la relación de
amortiguamiento se expresan como se indica en las ecuaciones 5.48 y 5.49.
ωn
BH
=
Yβ N r − N β Yr + UN β
ζ BH = −
U
1
2ω nDR
 Yβ + UN r

U




(5.48)
(5.49)
54
CAPÍTULO VI
CUALIDADES DE VUELO Y MANIOBRABILIDAD DE UNA
AERONAVE
El movimiento longitudinal incluye dos modos oscilatorios, el modo de período corto y
el modo de período largo. El movimiento latero direccional de una aeronave normalmente
consta de dos modos no oscilatorios, que son el modo de banqueo y el modo espiral y un
modo oscilatorio que es el llamado banqueo holandés. La relación de amortiguamiento para
cada uno de esos modos, y la frecuencia natural para los modos oscilatorios pueden ser
determinados de los autovalores, esos valores dependen de la geometría y propiedades de
masa de la aeronave tanto como de la derivadas aerodinámicas y de la velocidad de vuelo.
De esta manera el diseñador tiene control sobre las respuestas de amortiguamiento y
frecuencia natural de la aeronave alterando las variables mencionadas, sin embargo a la hora
de traducir esta respuesta a las cualidades de vuelo y maniobra de la aeronave, es necesario
centrarse en la opinión del piloto. En la mayoría de los casos, la opinión del piloto puede ser
subjetiva y difícil de cuantificar y medir es por esto que la Administración Nacional de
Aeronáutica y espacio de los Estados Unidos (National Aeronautics and Space
Administration, NASA), en apoyo de los departamentos de defensa y la industria de aviación
del mismo país, llevaron a cabo extensas investigaciones dirigidas a la obtención de
herramientas que permiten evaluar de manera simple, basándose en la opinión de los
aviadores, las características dinámicas de la aeronave.
Los resultados de estas investigaciones dan origen a las escalas de Cooper y Harper
(1969) y a la de Oscilación Inducida por el Piloto, PIO (por sus siglas en inglés). La
herramienta mas usada para cuantificar la opinión del piloto es la escala de Cooper y Harper.
Esta clasificación consta de una escala que va del uno al diez; donde el número uno indica
55
excelentes cualidades de vuelo y el número diez incontrolables condiciones de manejabilidad.
La figura 6.1 muestra el algoritmo utilizado por esta clasificación.
Adecuado para seleccionar tarea u operación
requerida
Si
Característica de la aeronave →
Demanda del piloto en seleccionar la tarea u
operación requerida
Valoración
del piloto
Excelente, Altamente deseable → La
compensación del piloto no es un factor para la
actuación deseada
1
Bueno, Deficiencia despreciable → La
compensación del piloto no es un factor para la
actuación deseada
2
Mediano, deficiencias no placenteras → Es
requerida una mínima compensación del piloto
para la actuación deseada
3
Deficiencias molestas → Actuación adecuada
requiere moderada compensación del piloto
No
¿Es satisfactorio sin
mejoras?
Deficiencias
requieren
mejoras
4
Deficiencias moderadamente objetables →
Actuación adecuada requiere considerable
compensación del piloto
5
Muy objetable pero con deficiencias tolerables →
Actuación adecuada requiere extensiva
compensación del piloto
6
Si
¿Es adecuada la
actuación obtenida,
con un trabajo
tolerable del piloto?
No
Deficiencias
advierten
mejoras
Deficiencias Mayores → No son alcanzadas
adecuadas actuaciones con una compensación
tolerable del piloto. La controlabilidad no es
cuestionable
7
Deficiencias mayores → Es requerida una intensa
compensación del piloto para mantener el control
8
Deficiencias Mayores → Es requerida una
considerable compensación del piloto para
mantener el control
9
Deficiencias Mayores → El control se pierde
durante algunas porciones de operación requerida
10
Si
¿Es controlable?
No
Mejoras
mandatarias
Decisión del piloto
Figura 6.1: Escala de clasificación Cooper y Harper, de las cualidades de vuelo.
56
En base a la escala de Cooper y Harper se han creado diversas normas que se derivan
de la evaluación de las cualidades de vuelo para diferentes tipos de aeronaves. Para este
estudio en específico serán empleadas las normas descritas en el reporte técnico del
laboratorio de dinámica de vuelo de la fuerza aérea de los EE.UU, titulado: Criterios de diseño
para cualidades de vuelo de vehículos aéreos remotamente pilotados (RPV Flying Qualities
Design Criteria) (Prosser, y Wiler, 1976).
Clasificación de las Aeronaves para Calificar sus Cualidades de Vuelo
Las cualidades de vuelo esperadas por el piloto dependen del tipo de aeronave y la fase
de vuelo. Las aeronaves son clasificadas de acuerdo a su tamaño y maniobrabilidad; en Clases
I, II, III y IV, y de acuerdo a la tarea que debe cumplir el piloto, y la de fase de vuelo en que se
encuentre (despegue, aterrizaje, ascenso y descenso) en categorías; A, B y C.
Según la Tarea del Piloto y la Fase de Vuelo en que se Encuentre
De acuerdo a la tarea del piloto, la clasificación de fase de vuelo se divide en tres
categorías, las categorías A, B y C.
Categoría A
Se refiere a una fase de vuelo no terminal que requiere rápida maniobra, precisión de
seguimiento, o un control preciso del sendero de vuelo. En esta categoría se incluyen
aeronaves de combate aire-aire, de ataque a tierra, reconocimiento aéreo, que reciben
reabastecimiento de combustible en vuelo, búsqueda antisubmarina y de vuelo en formación
cerrada.
Categoría B
Es una fase de vuelo no terminal que va normalmente acompañada de maniobras
graduales y sin precisión de seguimiento, en esta categoría esta incluido el vuelo en ascenso,
de crucero, de reabastecimiento de combustible, descenso, descenso de emergencia y de
entrega aérea.
57
Categoría C
Incluye fases de vuelo terminal que son normalmente acompañados de maniobras
graduales y usualmente requieren aproximación al sendero de vuelo, se incluyen en esta
categoría el despegue, aterrizaje, aproximación y la catapulta de despegue.
Según el Tamaño y tipo de Aeronave
Según el tamaño y tipo de aeronave se clasifican en Clases I, II, III y IV.
Clase I
Esta representada por aeronaves pequeñas y ligeras; utilidad ligera, de entrenamiento
primario y observación ligera.
Clase II
Aeronaves de peso mediano, de baja a media maniobrabilidad, que son de utilidad
pesada, de búsqueda y rescate, de carga y transporte ligera o mediana, antisubmarinas, de
reconocimiento, de ataque pesado, de bombas tácticas y de asalto a trasporte.
Clase III
Aeronaves grandes, pesadas de baja a media maniobrabilidad, tales como aeronaves de
transporte o carga pesada, de bombas pesadas, patrulleras, de transmisión de comunicaciones.
Clase IV
Aeronaves de alta maniobrabilidad tales como; interceptoras de fuego, de ataque, de
reconocimiento táctico y de observación.
58
Según la clasificación mostrada, la aeronave en estudio se encuentra enmarcada en una
aeronave de clase I y debe ser evaluada en las fases de vuelo identificadas como categorías B
y C.
Análisis de las Cualidades de Vuelo de una Aeronave
Las cualidades de vuelo de la aeronave son especificadas en término de niveles, Nivel
Uno; indica cualidades de vuelo claramente adecuadas para la misión, Nivel Dos; indica
cualidades de vuelo adecuadas para el cumplimiento de la misión pero con algún incremento
en la carga del piloto, degradación en la misión o ambas y Nivel Tres; que indica cualidades
de vuelo que permiten controlar la aeronave de manera segura pero con excesiva carga de
trabajo para el piloto, la efectividad en la misión es inadecuadada o ambas.
Período corto
El modo de período corto se comprende inicialmente de oscilaciones de alta frecuencia
en ángulo de ataque y desplazamiento vertical, así la velocidad de la aeronave permanece
cercanamente constante y la aceleración normal, causada por la sustentación, debida a los
cambios oscilatorios en ángulo de ataque, será denominada aceleración sensitiva, y es el
parámetro de sensibilidad en el estudio de este modo oscilatorio, de la misma manera, el
cuadrado de la frecuencia natural no amortiguada dividida por la aceleración sensitiva es un
importante parámetro de correlación asociado al modo de período corto, las ecuaciones 6.1 y
6.2 muestran la aceleración sensitiva y el parámetro de anticipación de control (CAP)
respectivamente.
CAP ≡
∂n
1 ∂L
1 ∂C L
=
=
∂α W ∂α CW ∂α
(6.1)
(ω n ) 2 sp (ω n ) 2 sp
(ω n ) 2 sp
=
=
∂n ∂α
L, α W C L ,α CW
(6.2)
El análisis del comportamiento de vuelo en período corto, para esta clase de aeronave
en las categorías mencionadas, se encuentran ilustrados en las figuras 6.2, 6.3, 6.4 y 6.5.
59
Frecuencia natural no amortiguada para periodo corto
100
Nivel 3
10
Nivel 2
Nivel 1
1
Nivel 4
Nivel 2
0.1
1
10
100
Sensibilidad de aceleración
Figura 6.2: Requerimientos de frecuencia y amortiguamiento en período corto, para
categoría de vuelo B y aeronaves de todas las clases. Fuente: Hodgkinson (1998).
60
Nivel 2
10
Nivel 3
Frecuencia natural no amortiguada para periodo corto
100
Nivel 1
1
Nivel 4
0.1
1
10
100
Sensibilidad de aceleración
Figura 6.3: Requerimientos de frecuencia y amortiguamiento en período corto, para
categoría de vuelo C y aeronaves de clase I y II. Fuente: Hodgkinson (1998).
61
Parámetro de control de anticipación (CAP)
100
Nivel 3
10
Nivel 2
Nivel 1
1
Nivel 4
0.1
0.1
1
10
Relación de amortiguamiento para periodo corto
Figura 6.4: Requerimientos de frecuencia y amortiguamiento en período corto, para fases de
vuelo de categoría B y aeronaves de todas las clases. Fuente: Hodgkinson (1998).
62
Parametro de control de anticipación (CAP)
100
Nivel 3
10
Nivel 2
1
Nivel 1
0.1
Nivel 4
0.01
0.1
1
10
Relación de amortiguamiento para periodo corto
Figura 6.5: Requerimientos de amortiguamiento y frecuencia en período corto, para
categoría C y aeronaves de todas las clases con una aceleración sensitiva mayor a 5g/rad.
Fuente: Hodgkinson (1998).
Período Largo
El análisis del comportamiento en período largo, para esta clase de aeronave en las
categorías mencionadas, se obtiene de la tabla 6.1.
Tabla 6.1: Requerimientos de amortiguamiento en período largo para toda clase de aeronave.
Fuente: Hodgkinson (1998).
1
Todas las fases de vuelo para todas las categorías
(mínimo amortiguamiento en período largo)
Relación de amortiguamiento debe ser mayor a 0,04
2
Relación de amortiguamiento debe ser mayor a 0,00
3
Tiempo para doblar la amplitud debe ser mayor que 55 segundos
Nivel
63
Modo de Banqueo
El análisis del comportamiento en modo de banqueo, para esta clase de aeronave en las
categorías mencionadas, se ilustra en la tabla 6.2.
Tabla 6.2: Requerimientos de amortiguamiento en modo de banqueo, máximo tiempo
constante (1/σ) en segundos. Fuente: Hodgkinson (1998).
Categoría Fase
de Vuelo
AyC
B
Clase de
Aeronave
I, IV
II, III
TODAS
Cualidades de Vuelo
Nivel 1
Nivel 2
Nivel 3
1.0
1.4
10
1.4
3.0
10
1.4
3.0
10
Modo Espiral
El análisis del comportamiento en vuelo de la aeronave en modo espiral, para la clase y
categorías mencionadas, puede obtenerse de la tabla 6.3.
Tabla 6.3: Requerimientos de amortiguamiento para el modo Espiral, mínimo tiempo para
doblar la amplitud en segundos. Fuente: Hodgkinson (1998).
Categoría Fase
de Vuelo
A
ByC
Clase de
Aeronave
I, IV
II, III
TODAS
Cualidades de Vuelo
Nivel 1
Nivel 2
Nivel 3
12
12
4
20
12
4
20
12
4
Modo de Banqueo Holandés
Las cualidades de vuelo de la aeronave en modo de banqueo holandés, se encuentra
ilustrada en la tabla 6.4.
64
Tabla 6.4: Requerimientos de Frecuencia y Amortiguamiento en el Modo de Banqueo
Holandés. Fuente: Hodgkinson (1998).
Nivel
Categoría
Fase de Vuelo
A
1
B
C
2
3
TODAS
TODAS
Clase de
Aeronave
IV-CO y AT
I, IV otros
II, III
TODAS
I, II-C, IV
II-L, III
TODAS
TODAS
Mínimo ζ
0,4
0,19
0,19
0,08
0,08
0,08
0,02
0,00
Mínimo ζ·ωn
(rad/s)
0,4
0,35
0,35
0,15
0,15
0,10
0,05
-
Mínimo ωn
(rad/s)
1,0
1,0
0,4
0,4
1,0
0,4
0,4
0,4
CO: Combate, AT: Ataque a tierra, C: Basado en un portaviones; L: bases en tierra
65
CAPÍTULO VII
RESULTADOS Y DISCUSIÓN
Estimación de las Derivadas de Estabilidad
Los coeficientes de estabilidad han sido obtenidos en el Capítulo IV y mostrados en la
tabla 4.6, la tabla 7.1 muestra los criterios de estabilidad estática de una aeronave en
comparación con los resultados obtenidos para el ANCE, en sus versiones X-3b y X-3c
haciendo uso del código Tornado Vortex Lattice.
La tabla 7.1 permite observar que el aeroplano en estudio es estable estáticamente en
todos sus ejes de movimiento luego de corregir los signos por diferentes sistemas de
coordenadas referencial utilizados, que se muestran en el apéndice A.
Tabla 7.1: Coeficientes aerodinámicos del ANCE X-3 y criterios de estabilidad.
Cm,α
Tornado
ANCE X-3b
-0,0475
Tornado
ANCE X-3c
-0,0476
Criterio de
Estabilidad
Cm,α < 0
Cℓ,β
-0,0003
-0,0003
Cℓ,β < 0
Cn,β
0,0027
0,0027
Cn,β > 0
Relación
Sabiendo que la aeronave es estable estáticamente y conociendo sus coeficientes de
estabilidad, han sido calculadas las derivadas de estabilidad longitudinal y latero direccionales.
Las tablas 7.2 y 7.3 muestran los resultados obtenidos de las derivadas de estabilidad
longitudinal y latero – direccional respectivamente.
66
Tabla 7.2: Derivadas de Estabilidad Longitudinal.
Xu =
-0,0184 (s-1)
Xw =
0,0973 (s-1)
Zu =
-0,3319 (s-1)
Zw =
-1,7688 (s-1)
Zα =
-72,840 (m/s2)
Zq =
1.7937 (m/s2)
Mu =
0 (1/m.s)
Mw =
-0,2416 (1/m.s)
M w& =
-0,0065 (m-1)
Mq =
-2,0002 (s-1)
Mα =
-9,9495 (s-1)
M δe =
-10,4512 (s-2)
Tabla 7.3: Derivadas de Estabilidad Latero –Direccional.
Yβ =
-7,3755 (m/s2)
YP =
0,062776 (m/s)
Yr =
-0,5381 (m/s)
NP =
-0,16937 (s-1)
Nβ =
4,8466 (s-2)
Nr =
-0,84687 (s-1)
Lβ =
-1,436 (s-2)
Lp =
-3,95206 (s-1)
Lr =
1,12916 (s-1)
Yδ a =
-0,0788 (m/s2)
Yδ r =
-3,57369 (m/s2)
Lδ a =
-17,2325 (s-2)
Nδ a =
0,538516 (s-2)
Nδ r =
4,667143 (s-2)
Lδ r =
-0,47868 (s-2)
Estudio Dinámico
El estudio dinámico ha sido desacoplado en estudio de la dinámica longitudinal y
estudio de la dinámica latero - direccional, en ambas se asume la aeronave como un cuerpo
rígido y sus ecuaciones características han sido descritas en el Capítulo V.
Estabilidad Dinámica Longitudinal
Sustituyendo las derivadas de estabilidad longitudinal mostradas en la tabla 7.2, en la
ecuación 5.21 han sido obtenidos los autovalores de lo movimientos oscilatorios
longitudinales de período corto y de período largo que se muestran en las ecuaciones 7.1 y 7.2
respectivamente.
67
λ1, 2 = −2,0245 ± 3,067 i
(7.1)
λ1, 2 = −0,0036 ± 0,2413 i
(7.2)
Las ecuaciones 7.1 y 7.2 muestran que la aeronave responde de manera amortiguada a
ambos modos oscilatorios de período largo y de período corto.
Aproximación al Modo de Período Corto
Los autovalores obtenidos de la ecuación característica de este movimiento, presentada
en la ecuación 5.33, se muestran en la ecuación 7.3.
λ1, 2 = −2,018962 ± 3,067807 i
(7.3)
La tabla 7.4 muestra la frecuencia natural no amortiguada y la relación de
amortiguamiento obtenidos de las aproximaciones longitudinales en período corto del ANCE
X-3.
Tabla 7.4: Aproximaciones longitudinales en período corto.
ω nsp
3,6725 rad/s
ς sp
0,5497
De este estudio se observa que la respuesta de la aeronave al modo de período corto es
amortiguada, siendo su solución un movimiento sinusoidal cuya amplitud decrece
exponencialmente con el tiempo.
Aproximación al Modo de Período Largo
La ecuación característica de este modo se muestra en la ecuación 5.30 y los
autovalores obtenidos para este modo se muestran en la ecuación 7.4.
λ1, 2 = −0,009184 ± 0,281077 i
(7.4)
68
Se observa que la aeronave presenta una respuesta amortiguada al período largo con
una frecuencia natural no amortiguada y una relación de amortiguamiento, como se observan
en la tabla 7.5.
Tabla 7.5: Aproximaciones longitudinales en período largo.
ω np
ςp
0,2812 rad/s
0,03266
La tabla 7.6 muestra un resumen de las aproximaciones longitudinales en período largo
y período corto y la solución exacta representada en la ecuación 5.21 para cada uno de los
modos.
Tabla 7.6: Comparación de métodos aproximados y solución exacta al modo longitudinal.
Período
Largo
Período Corto
t1/2 (s)
Aproximación
75,1267002
Solución Exacta
191,6666667
Т (s)
22,35396333
26,03889477
ζp
0,032658611
0,014917528
ωnp (rad/s)
0,281227032
0,241326853
N1/2 (ciclos)
3,360777644
7,360783489
t1/2 (s)
0,341759735
0,340824895
Т (s)
2,048103507
2,048642096
ζsp
0,54974353
0,55089528
ωnsp (rad/s)
3,672552984
3,674927108
N1/2 (ciclos)
0,166866437
0,166366246
La tabla 7.6 muestra una excelente correlación entre los valores obtenidos haciendo
uso de las aproximaciones longitudinales al período corto con respecto a la solución exacta,
sin embargo se observa que para el modo de período largo los resultados solo presentan una
buena correlación en el cálculo de la frecuencia natural no amortiguada y el período, mientras
que el tiempo y número de ciclos para llevar a la mitad de la amplitud y relación de
amortiguamiento muestran una correlación deficiente, en el caso específico del estudio del
ANCE X-3, esto es debido a que en esta aproximación ha sido asumido que no existen
variaciones en el ángulo de ataque, sin embargo en el modo de período largo se producen
69
cambios en el ángulo de ataque, pero que son muy pequeños en comparación con la variación
de velocidad axial, éstas muy pequeñas variaciones en el ángulo de ataque pueden tener un
efecto significante en el movimiento de la aeronave (Phillips, 2004).
Estabilidad Dinámica Latero – Direccional
Al sustituir las derivadas de estabilidad latero - direccionales mostradas en la tabla 7.3
en la ecuación 5.36, han sido obtenidas las raíces de las ecuaciones características latero –
direccionales, estas consisten en dos raíces reales y un par de raíces complejas. Las ecuaciones
7.5, 7.6 y 7.7 muestran los autovalores característicos de los movimientos; oscilatorio
ligeramente amortiguado con baja frecuencia banqueo holandés, altamente convergente ó
modo de banqueo y lentamente convergente o divergente o modo de espiral respectivamente.
λ1, 2 = −0,5338 ± 2,245 i
(7.5)
λ3 = −3,9585
(7.6)
λ4 = 0,0481
(7.7)
Aproximación al Movimiento Espiral
El estudio del movimiento espiral ha sido desarrollado utilizando las aproximaciones
recomendadas por Phillips (2004), de esta manera haciendo uso de la ecuación 5.41 y
sustituyendo los valores de las derivadas de estabilidad latero direccionales presentados en la
tabla 7.3, se obtiene el autovalor del modo espiral que se muestra en la tabla 7.7, en ella
también se observan la tasa de amortiguamiento y el tiempo constante máximo.
Tabla 7.7: Métodos aproximados al modo espiral.
Aproximación
λ Espiral
0,003318
σ
-0,05269
1σ
13,1558
70
Aproximación al Banqueo
Utilizando las ecuaciones 5.44 y 5.45 han sido calculados el autovalor para el modo de
banqueo y la tasa de amortiguamiento obteniéndose un tiempo máximo constante de 0,016
segundos, la tabla 7.8 muestra la aproximación obtenida en modo de banqueo.
La tabla 7.8 muestra que luego de someter a la aeronave a una perturbación en el modo
de banqueo su respuesta tenderá a un modo convergente, que describirá un retorno
exponencial al equilibrio.
Tabla 7.8: Aproximación al modo de banqueo.
λGiro
-3,9585
σ
62,85368
1
0,01591
σ
Aproximación al Banqueo Holandés
La ecuación característica del modo de banqueo holandés se encuentra expresada en la
ecuación 5.47, sustituyendo las derivadas latero direccionales han sido obtenidas las raíces
asociadas a este movimiento, y se muestran en la ecuación 7.8.
λ BH = −0,5338 ± 2,2458 i
(7.8)
De la ecuación 7.8, se observa que al someter a la aeronave a una perturbación en este
modo la respuesta será amortiguada. En la tabla 7.9 se muestran los valores de frecuencia
natural no amortiguada y la relación de amortiguamiento obtenidos de esta aproximación.
Tabla 7.9: Aproximación al modo de banqueo holandés.
ωn
ς BH
ω n ⋅ ζ BH
BH
BH
2,30758
0,23132
0,5338
71
La tabla 7.10 muestra un resumen de las características latero - direccionales obtenidas
de la solución exacta y haciendo uso de las aproximaciones, la tabla muestra una excelente
correlación de la aproximación utilizada para el modo de banqueo con la solución exacta de
alrededor de un 99,9%, una buena correlación de los resultados obtenidos al usar la
aproximación para el modo de banqueo holandés de un 95,4% para el cálculo de la relación de
amortiguamiento y de un 98,56% en el resultado obtenido de la frecuencia natural no
amortiguada. En la comparación para el movimiento espiral se observa que no existe
correlación alguna para el caso en estudio, sin embargo se observa que los autovalores
obtenidos en ambos casos son de signo positivo, por lo que se asume que si la aeronave es
sometida a una perturbación en este modo su repuesta corresponderá a un movimiento espiral
divergente.
Tabla 7.10: Comparación de métodos aproximados y solución exacta al modo latero –
direccional.
Aproximación
2,20151
Solución Exacta
2,30758
ς BH
0,2280
0,23132
ω n ⋅ ζ BH
0,4234
0,5338
σ
62,7515
62,8536
1
σ
σ
0,0159
0,0159
-0,05268
-0,7637
ln(0,5) / σ
13,1558
0,9075
ωn
BH
BH
Modo
Banqueo
Holandés
Banqueo
Espiral
Cualidades y Maniobra de Vuelo de la Aeronave
Según la clasificación mostrada, la aeronave en estudio se encuentra enmarcada en una
aeronave de clase I y debe ser evaluada en las fases de vuelo identificadas como categorías B
y C.
72
Análisis de las Cualidades de Vuelo de la Aeronave
Período corto
La tabla 7.11 muestra los valores de aceleración sensitiva y el parámetro de
anticipación de control, descritos en las ecuaciones 6.1 y 6.2 respectivamente. Con estos
valores, la frecuencia natural no amortiguada y la relación de amortiguamiento en período
corto han sido analizadas las cualidades de vuelo de la aeronave en período corto, haciendo
uso de las figuras 6.2, 6.3, 6.4 y 6.5.
Tabla 7.11: Parámetros representativos del estudio longitudinal.
nα
7,425124
CAP
1,818836
Teniendo como valores de entrada la aceleración sensitiva y la frecuencia natural no
amortiguada en período corto, se observa en la figura 7.1 que para vuelo en crucero, vuelo en
ascenso, descenso y maniobras graduales sin precisión, la aeronave se desenvuelve en el Nivel
I, lo que se traduce en excelentes cualidades de vuelo para esta misión en específico.
73
Figura 7.1: Localización del nivel de cualidad de vuelo en período corto para la categoría de
vuelo B del ANCE X-3 sin potencia.
La figura 7.2 indica los requerimientos de frecuencia de la aeronave para el estudio de
las cualidades de vuelo en fases de despegue, aterrizaje y aproximación. Para la aeronave en
estudio se observa que las cualidades de vuelo en esta categoría se encuentran en Nivel I.
74
Figura 7.2: Localización del nivel de cualidad de vuelo en período corto para la categoría de
vuelo C del ANCE X-3 sin potencia.
Para esta aeronave la aceleración sensitiva es lo suficientemente grande como para que
los requerimientos de frecuencia dependan del parámetro de anticipación, por esto la aeronave
será analizada nuevamente en las mismas categorías de vuelo (categorías B y C), combinando
los requerimientos de relación de amortiguamiento y parámetro de anticipación, como se
muestran en las figuras 7.3 y 7.4.
Se observa en la figura 7.3 muestra, que teniendo como datos de entrada la relación de
amortiguamiento y el parámetro de anticipación, la aeronave posee excelentes cualidades de
vuelo en la categoría B al igual que se observa en la figura 7.1.
75
Figura 7.3: Localización del nivel de cualidad de vuelo en período corto para la categoría de
vuelo B del ANCE X-3 sin potencia.
La figura 7.4 permite analizar las cualidades de vuelo de la aeronave teniendo como
parámetros de observación el parámetro de anticipación y la relación de amortiguamiento en
período corto, teniendo en cuenta que la aceleración sensitiva de la aeronave debe ser mayor a
cinco unidades.
La figura 7.4 muestra que tomando en cuenta estos parámetros la aeronave pasa a
ocupar un nivel dos en cualidades de vuelo y maniobra en la categoría de despegue, aterrizaje,
y aproximación, lo que indica que las cualidades de vuelo son adecuadas para estas maniobras,
pero el piloto debe incrementar su carga de trabajo para el cumplimiento de estas tareas.
76
Figura 7.4: Localización del nivel de cualidad de vuelo en período corto para categoría de
vuelo C del ANCE X-3 sin potencia con una aceleración sensitiva mayor a 5g/rad.
Período Largo
Con una relación de amortiguamiento en período largo igual 0,0149 para la solución
exacta ó de 0,033 para la aproximación, como se muestra en la tabla 7.6, la aeronave en
estudio se encuentra en el nivel 2, lo que implica que el aeroplano ofrece buenas cualidades de
respuesta ante una perturbación en período largo, según puede ser observado en la tabla 6.1
Modo de Banqueo
El tiempo constante (1/σ) en segundos obtenido del estudio de la aeronave es de 0,0159
tal como lo muestra la tabla 7.10, analizando esto según lo observado en la tabla 6.2, el
aeroplano se encuentra en nivel 1, lo que indica que posee excelentes cualidades de vuelo en
modo de banqueo.
77
Modo de Banqueo Holandés
Los resultados obtenidos luego de evaluar el ANCE, pueden observarse en la tabla 7.8
y 7.10, con una frecuencia natural no amortiguada de 2,3, una relación de amortiguamiento de
0,213, según la tabla 6.4 el ANCE X-3 se encuentra delimitado en el nivel 1 en las categorías
B y C.
Modo Espiral
Para el estudio en espiral, han sido verificados los valores de tiempo para doblar la
amplitud, mostrados en la tabla 7.10 en la tabla 6.3, mostrando la aproximación que la
aeronave ofrece buenas cualidades de vuelo (nivel 2), sin embargo se observa que la solución
exacta muestra que el tiempo de respuesta para doblar la amplitud es muy pequeño, por lo que
se entiende que la aeronave no posee buenas cualidades de vuelo en modo espiral, poniendo en
riesgo la efectividad de la tarea a desarrollar según la categoría de vuelo en que se encuentre.
Según explican Nelson (1998) y Phillips (2004), lograr que una aeronave posea buenas
características en los modos espiral y banqueo holandés a la vez, puede convertirse en un gran
reto para un diseñador, esto se debe a que si se incrementa la estabilidad de banqueo se
consigue un buen efecto en el amortiguamiento en espiral mientras que se desmejora la
amortiguación en banqueo holandés. Si se incrementa la estabilidad en guiñada mejora la
amortiguación pero hace al modo espiral mucho mas inestable, solo incrementando la
amortiguación en guiñada se puede obtener un efecto favorable en la amortiguación del
banqueo holandés y del modo espiral. Desafortunadamente incrementar la amortiguación de
guiñada sin incrementar la estabilidad de guiñada no es sencillo, requiere un incremento del
tamaño de la cola, lo que aumentaría significativamente la resistencia y el peso.
En la actualidad este problema es resuelto en las aeronaves, colocando superficies
verticales adelantadas al centro de gravedad, o utilizando dispositivos de control automático.
Colocar superficies verticales adelantadas al centro de gravedad aumenta significativamente la
resistencia de la aeronave por lo que generalmente no son utilizadas.
78
Se hace necesario recalcar que los métodos utilizados para determinar los coeficientes
de estabilidad no son exactos como lo demostraron Razgonyaev y Mason (1995). En su
investigación se compararon datos obtenidos de pruebas de vuelo del XB-70 con los obtenidos
haciendo uso de Datcom, del código JKay VLM; basado en el método vortex lattice y el
código APAS; un programa basado en el método de los paneles. Para regímenes subsónicos se
obtuvo una buena correlación para CL,α, Cm,α, CY,β, Cm,q y Cℓ,p, pero una deficiente correlación
entre los métodos de estimación y los pruebas de vuelo para Cn,β y Cℓ,β. Así mismo Bray
(1991) compara resultados de las pruebas en túnel de viento realizadas sobre el Pioneer RQ2B con resultados obtenidos en el mismo avión utilizando el método de los paneles PMARC
(Lyons, 1989). En este se observa una buena correlación entre los resultados obtenidos de CL,α
y Cm,α, y una correlación deficiente para Cn,β y Cℓ,β.
La respuesta que se obtiene del movimiento espiral se encuentra estrechamente ligada a
los coeficientes aerodinámicos de momento de guiñada y de banqueo, respecto al ángulo de
deslizamiento Cn,β y Cℓ,β, de esta manera las raíces obtenidas para espiral, de la interacción
latero – direccional mostrada en la ecuación 5.36, así como de las aproximaciones mostradas
en las ecuaciones 5.40, 5.41 y 5.42, pueden tener un gran margen de error con respecto a el
comportamiento real de la aeronave en pruebas de vuelo.
Para el ANCE X-3 se recomienda verificar mediante pruebas de vuelo la respuesta de
la aeronave ante una perturbación que induzca a un movimiento espiral, y dependiendo del
resultado obtenido, sean discutidos el rediseño del empenaje de cola o la implementación de
un sistema de control automático que permita aumentar la amortiguación en guiñada, sin
modificar sus características geométricas.
79
CAPÍTULO VIII
CONCLUSIONES
El estudio de la estabilidad estática del Avión No Tripulado de Conservación
Ecológica (ANCE), consistió de un análisis estático y uno dinámico, ambos desacoplados en
estudio longitudinal y latero–direccional. Las fuerzas y momentos actuantes sobre la aeronave
en vuelo han sido obtenidas haciendo uso del código Tornado, luego de validar el modelo
computacional, comparando los coeficientes de fuerzas resultantes con los obtenidos
empleando PAN AIR (A502i), Digital Datcom y ensayos en el túnel del viento.
Los coeficientes de estabilidad de la aeronave, muestran una respuesta de tendencia al
estado de equilibrio luego de sufrir una perturbación en cualquiera de sus tres ejes de
movimiento, con lo que se concluye que el ANCE X-3 es estable estáticamente en sus dos
versiones X-3b y X-3c.
El estudio dinámico de la aeronave revela para su eje longitudinal en sus dos modos,
período corto y período largo, una respuesta estable y amortiguada, que puede ser descrita con
un movimiento sinusoidal teniendo una amplitud que decrece con el tiempo.
En el análisis del comportamiento dinámico han sido evaluadas las respuestas
producidas por el ANCE X-3, al ser sometido a pequeñas perturbaciones de su estado de vuelo
de equilibrio. Se concluye que la aeronave es estable dinámicamente en las tendencias que
produce en el modo de banqueo y en el modo de banqueo holandés, mientras que al modo
espiral se manifiesta con un movimiento divergente que proporciona inestabilidad.
Las cualidades de vuelo y maniobrabilidad de la aeronave en su eje longitudinal en
período corto son excelentes para vuelo en crucero, en ascenso y descenso mientras que
durante el despegue y el aterrizaje las cualidades de vuelo del ANCE pueden mostrarse de
buenas a excelentes. En período largo la aeronave muestra buenas cualidades de vuelo.
80
Las cualidades latero–direccionales del ANCE se muestran excelentes para los modos
de banqueo y de banqueo holandés, mientras que en el movimiento espiral el tiempo de
respuesta para doblar la amplitud es demasiado corto por lo que no posee cualidades de vuelo
en este modo.
De este estudio se concluye que el ANCE es lo suficientemente estable como para
proseguir con el avance del diseño, específicamente con el estudio del comportamiento
dinámico de la aeronave en pruebas de vuelo. De las respuestas obtenidas de estas se
recomienda discutir el rediseño del empenaje de cola, o la implementación de un sistema de
control automático que permita corregir la amortiguación en guiñada.
81
REFERENCIAS BIBLIOGRÁFICAS
Bertin, J. J., y Smith, M. L. (1998). Aerodynamics for Engineers, 3era ed. Upper Saddle River,
New Jersey, EE.UU: Prentice Hall.
Boschetti, P., y Cárdenas, E. (2003). Diseño de un Avión No Tripulado de Conservación
Ecológica. Trabajo final de Grado. Maracay, Venezuela: Universidad Nacional
Experimental Politécnica de la Fuerza Armada.
Boschetti, P. (2006). Reducción de Resistencia Aerodinámica en el Avión No Tripulado de
Conservación Ecológica. Trabajo de Grado de Maestría. Caracas, Venezuela:
Universidad Simón Bolívar.
Boschetti, P., Cárdenas, E., y Amerio, A. (2006). Drag Clean – up Process of the Unmanned
Airplane for Ecological Conservation, Aerotecnica Missile e Spazio, 85 (2), 53-62.
Boschetti, P., Cárdenas, E., y Amerio, A. (2008a, abril). Calculo de las Características
Aerodinámicas de un Avión No Tripulado Empleando el Método de los Paneles. Ponencia
presentada en “IX Congreso Internacional de Métodos Numéricos Ingeniería y Ciencias”.
Isla de Margarita, Venezuela.
Boschetti, P., Cárdenas, E., y Amerio, A. (2008b). Increasing the Lift – Drag Ratio of an
Unmanned Aerial Vehicle using Local Twist, Journal of Aircraft, 45 (1), 10-15.
Bray, R. M. (1991). A Wind Tunnel Study of the Pioneer Remotely Piloted Vehicle. Tesis de
Maestría. Monterrey, California, EE.UU: Naval Postgraduate School.
Cárdenas, E., Boschetti, P., Amerio, A. y Velásquez, C. (2005, septiembre). Design of an
Unmanned Aerial Vehicle for Ecological Conservation. Ponencia presentada en
“Infotech@Aerospace” con el número AIAA-2005-7056. Arlington, Virginia, EE.UU.
Cárdenas, E., Boschetti, P., y Amerio, A. (2008, abril). Evaluación de la Estabilidad Estática
de un Avión No Tripulado Empleando el Método Vortex Lattice. Ponencia presentada en
“IX Congreso Internacional de Métodos Numéricos Ingeniería y Ciencias”. Isla de
Margarita, Venezuela.
Craidon, C. B. (1985). A Description of the Langley Wireframe Geometry Standard (LaWGS)
Format, NASA TM-85767. Washington D.C., EE.UU: National Aeronautics and Space
Administration.
82
Cooper, G. E. y Harper, R. P. (1969). The Use of Pilot Rating in the Evaluation of Aircraft
Handing Qualities, NASA TN D-5153. Washington D.C., EE.UU: National Aeronautics
and Space Administration.
Derbyshire T. y Sidwell K. W. (1982) PAN AIR Summary Document (Version 1.0). NASA CR3250. Washington D.C., EE.UU: National Aeronautics and Space Administration.
Finck, R. D. (1978). USAF Stability and Control Datcom (Data Compendium), ADB072482.
Saint Louis, Missouri, EE.UU: McDonnell Douglas Astronautics Company.
Foster, T. (2005). Dynamic Stability and Handling Qualities of Small Unmanned – Aerial –
Vehicles. Tesis de Maestría. Departamento de Ingeniería Mecánica. Provo, Utah; Estados
Unidos: Brigham Young University.
Hoak, D. E. (1960). USAF Stability and Control Datcom (Data Compendium), AFWAL-TR83-3048, Wright – Patterson Air Force Base, Ohio, EE.UU: McDonnell Douglas
Astronautics Company.
Hodgkinson, J. (1998). Aircraft Handling Qualities. Reston, Virginia, EE.UU: AIAA
Educational Series.
Lyons, D. F. (1989). Aerodynamic Analysis of a U.S. Navy and Marine Corps Unmanned Air
Vehicle. Tesis de Maestría. Monterrey, California, EE.UU: Naval Postgraduate School.
Madson, M. D. y Erickson, L. L. (1990) Toward the Routine Aerodynamic Analysis of
Complex Configurations. Editor: Henne, P. A. Applied Computational Aerodynamics.
Washington D.C., EE.UU: American Institute of Aeronautics and Astronautics.
Melin, T. (2000a). User’s guide and reference manual for Tornado. Estocolmo, Suecia:
Kungliga Tekniska Högskolan (KTH).
Melin, T. (2000b). A Vortex Lattice MATLAB Implementation for Linear Aerodynamic Wing
Applications. Tesis de Maestría. Estocolmo, Suecia: Kungliga Tekniska Högskolan.
Melin, T. (2006). Multidisciplinary Design in Aeronautics, Enhanced by SimulationExperiment Synergy, Tesis Doctoral. Estocolmo, Suecia: Kungliga Tekniska Högskolan.
Miranda L. R., Elliott, R. D., y Baker, W. M. (1977). A Generalized Vortex Lattice Method for
Subsonic and Supersonic Flow Applications, NASA CR-2865. Washington D.C., EE.UU:
National Aeronautics and Space Administration.
Nelson, R. C. (1998). Flight Stability and Automatic Control, 2da ed. Boston, Massachusetts,
EE.UU: McGraw Hill.
Phillips, W. F. (2004). Mechanics of Flight. Hoboken, New Jersey, EE.UU: John Wiley &
Sons, Inc.
83
Prosser, C. F., y Wiler, C. D. (1976). RPV Flying Qualities Design Criteria, AFFDL-TR-76125. Columbus, Ohio, EE.UU: Air Force Flight Dynamics Laboratory y Rockwell
International Corporation.
Razgonyaev V., y Mason W. H. (1995, enero). An Evaluation of Aerodynamic Prediction
Methods Applied to the XB-70 for Use in High Speed Aircraft Stability and Control
System Design. Ponencia presentada en “33rd Aerospace Sciences Meeting & Exhibit”
con el número AIAA-95-0759. Reno, Nevada, EE.UU.
Saaris, G. R. (1992). Technology Program for Solving Problems of Potential Flow about
Arbitrary Configurations: A501I User’s Manual – PAN AIR, D6 – 54703. Seattle,
Washington, EE.UU: The Boeing Company.
Sidwell, K. W., Baruah, P. K., Bussoletti, J. E., Medan, R.T., Conner, R. S., y Purdon, D. J.
(1990). PAN AIR- A Computer Program for Predicting Subsonic or Supersonic Linear
Potential Flows About Arbitrary Configurations Using a Higher Order Panel Method
Volume II - User's Manual (Version 3.0), NASA CR-3252 Washington D.C., EE.UU:
National Aeronautics and Space Administration.
Two Stroke International. (2001). Engine Models 460F-35 and 460 FE-35. Recuperado en
marzo 9 de 2003, disponible en: http://www.2si.com/
Williams, J. E., y Vukelich, S. R. (1979). The USAF Stability and Control Digital Datcom,
Vol. 1, Users Manual, AFFDL-TR-79-3032. Saint Louis, Missouri, EE.UU: Air Force
Flight Dynamics Laboratory y McDonnell Douglas Astronautics Company. Actualizado
por: Public Domain Aeronautical Software. (1999). Santa Cruz, California, EE.UU.
84
APÉNDICE A
SISTEMA REFERENCIAL DE COORDENADAS DE LA AERONAVE
Durante el desarrollo de esta investigación han sido utilizados como referencia
principal, los trabajos de Warren Phillips y Robert Nelson. Las derivadas de estabilidad han
sido obtenidas haciendo uso del código Tornado versión T131b, y han sido comparadas con
las obtenidas haciendo uso del software de fuente abierta PAN AIR (A502i).
Cada uno de estos autores define para el estudio el sistema de referencia utilizado, las
figuras A.1 y A.2, muestran el sistema referencial de coordenadas para la aeronave, empleados
por Robert Nelson y Warren Phillips respectivamente, se observa que utilizan el mismo
sistema referencial.
Figura A.1: Sistema de referencia de coordenadas utilizado por Robert Nelson. Fuente:
Nelson (1998).
El sistema referencial empleado por los códigos utilizados puede observarse en las
figuras A.3 y A.4, La figura A.3 muestra el sistema referencial de coordenadas empleado en el
85
código Tornado, y la figura A.4 muestra el sistemas de coordenadas referencial contenido en
el software PAN AIR. En estas figuras se observa que ambos códigos utilizan el mismo
sistema referencial.
Figura A.2: Sistema de coordenadas, convención de signos para ángulos y momentos
aerodinámicos actuantes en una aeronave en vuelo libre. Fuente: Phillips (2004).
La figura A.5 muestra el sistema de coordenadas referencial utilizada en el estudio de
la estabilidad del ANCE. Con este sistema serán corregidos signos de los valores de
coeficientes de estabilidad arrojados por los códigos utilizados
86
Figura A.3: Sistemas de coordenadas en una aeronave en vuelo libre empleado en el código
Tornado Vortex Lattice. Fuente: Melin (2000a).
Figura A.4: Sistemas de coordenadas, convención de signos para ángulos y momentos
aerodinámicos actuantes en una aeronave en vuelo libre empleado en el software PAN AIR.
Fuente: Sidwell, et al (1990).
87
Figura A.5: Sistema de referencia de coordenadas utilizadas para el estudio del ANCE.