COMPARACIONES PAREADAS Si aceptamos H1 aún nos interesa

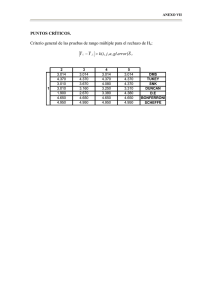
COMPARACIONES PAREADAS
Si aceptamos H1 aún nos interesa saber cuáles medias son iguales y
cuáles son distintas. Para el caso de k medias, habrá c =[k (k-1)/2]
contrastes posibles.
Prueba LSD de Fisher
Se basa en el ensayo “t” de significación de diferencia de medias.
Calcula la “menor diferencia significativa” (least significant
difference) entre dos medias cualesquiera del conjunto analizado
mediante un ANAVA.
2
∆ LSD = t ( α ; φ error ) serror
n
H0 : y i = y j
para i ≠ j
H1 : y i ≠ y j
Si y i − y j ≥ ∆ LSD
⇒ las medias difieren al nivel de significación α
Al realizar numerosas comparaciones supuestamente independientes
la tasa de error experimento – juicio, TEEJ (probabilidad de rechazo
equivocado de al menos una de las hipótesis nulas verdaderas)
aumenta.
TEEJ = 1 – (1 - α)c , siendo α la probabilidad seleccionada del error
tipo I para una comparación específica.
Así, para k = 4 , c =6 y α= 0.05 ⇒ TEEJ = 1-0.956 = 0.26
Es el menos conservador de los procedimientos.
Test de Bonferroni
Define un nivel de significación ajustado:
α ajustado =
α
nº decomparac iones
α= nivel de significación deseado
Se realiza igual que el LSD, pero con αajustado:
∆ Bonferroni = t ( α ajustado ; φ error ) serror
H0 : y i = y j
2
n
para i ≠ j
H1 : y i ≠ y j
Si
y i − y j ≥ ∆ Bonferroni
⇒ las medias difieren al nivel de
significación α
Inconveniente: Las tablas no presentan los estadísticos t para cualquier
α.
Prueba de Tukey ( o HSD, honestly significantly difference)
Define un estadístico q = q(α,φerror, nº de medias)
Calcula: ∆ Tukey = q( α , φ error , k ). serror .
1
nA
donde n A es la media armónica del tamaño de los grupos i – j en
comparación.
H0 : y i = y j
para i ≠ j
H1 : y i ≠ y j
Si
y i − y j ≥ ∆ Tukey
⇒ las medias difieren al nivel de
significación α
Es el más conservador de los procedimientos, mantiene la TEEJ al
nivel deseado pero pierde Potencia (probabilidad de rechazar la H0
falsa).
Procedimiento de Duncan
Define un estadístico D:
D = D (α,φerror, nº de medias ordenadas abarcadas en la comparación)
Se ordenan las medias de menor a mayor y se determina el número de
medias abarcadas en cada comparación.
H0 : y i = y j
para i ≠ j
H1 : y i ≠ y j
Se calcula: ∆ Duncan = D . serror .
Si
y i − y j ≥ ∆ Duncan
1
n
⇒ las medias difieren al nivel de
significación α
Inconveniente:
TEEJ = 1 – (1 - α) k-1, alta. Se llega a conclusiones parecidas al LSD
pero es más engorroso.
Procedimiento de Neuman-Keuls
1) Se ordenan las k medias de menor a mayor y se comparan por el
procedimiento de Tukey las dos de los extremos.
2) Si difieren significativamente se continuan las comparaciones.
Por ejemplo: y 1 < y 2 < y 3 < y 4
∆ Tukey = q( α , φ error ,4 ). serror .
1
nA
y ensayo H0: y 1 = y 4
H 1: y 1 ≠ y 4
> ∆ Tukey ⇒ y 1 ≠ y 4
Si
y1 − y 4
Ensayo
H0: y 1 = y 3
;
H1: y 1 ≠ y 3
y
H0: y 2 = y 4
;
H1: y 2 ≠ y 4
Recalculando
∆ Tukey = q( α , φ error ,3 ). serror .
1
nA
Si rechazo ambas hipótesis nulas ensayo:
H0 : y 1 = y 2
;
H1: y 1 ≠ y 2
H0 : y 2 = y 3
;
H1: y 2 ≠ y 3
H0 : y 3 = y 4
;
H1: y 3 ≠ y 4
utilizando ∆ Tukey = q( α , φ error ,2 ). serror .
1
nA
Es un ensayo que controla mejor el TEEJ que el test de LSD y tiene
mejor Potencia que el test de Tukey.
Recapitulación y recomendaciones
No hay un procedimiento “correcto”, cada uno tiene ventajas y
desventajas, si disminuyo la probabilidad de rechazar la H0 verdadera
(TEEJ) disminuyo también la probabilidad de rechazar la H0 falsa
(Potencia).
El tipo de cálculo es similar en todos los métodos, difieren en los
valores críticos utilizados.
Valor
crítico
nj=4
nº de medias abarcadas
Los procedimientos de Fisher (LSD) y Duncan mantienen la TEEJ
muy alta y no son aconsejables.
Recuerda que:
Aceptar la hipótesis nula ⇒ que no hay evidencia que la refute.
Rechazar la hipótesis nula ⇒ que la evidencia de la muestra la
refuta.
Comparación de medias con un control
Test de Dunnett
Se desea comparar las medias de varios grupos de tratamientos con la
media de un grupo control.
Define un estadístico:
d = d (α; φerror; k-1)
∆ Dunnett = d ( α , φ error ). s error .
H0: y i = y control
2
n
para i ≠ control
H1: y i ≠ y control
Si
y i − y control ≥ ∆ Dunnett
significación α
⇒ las medias difieren al nivel de