5. CRECIMIENTO ECONÓMICO 5.apéndice Tasas de crecimiento

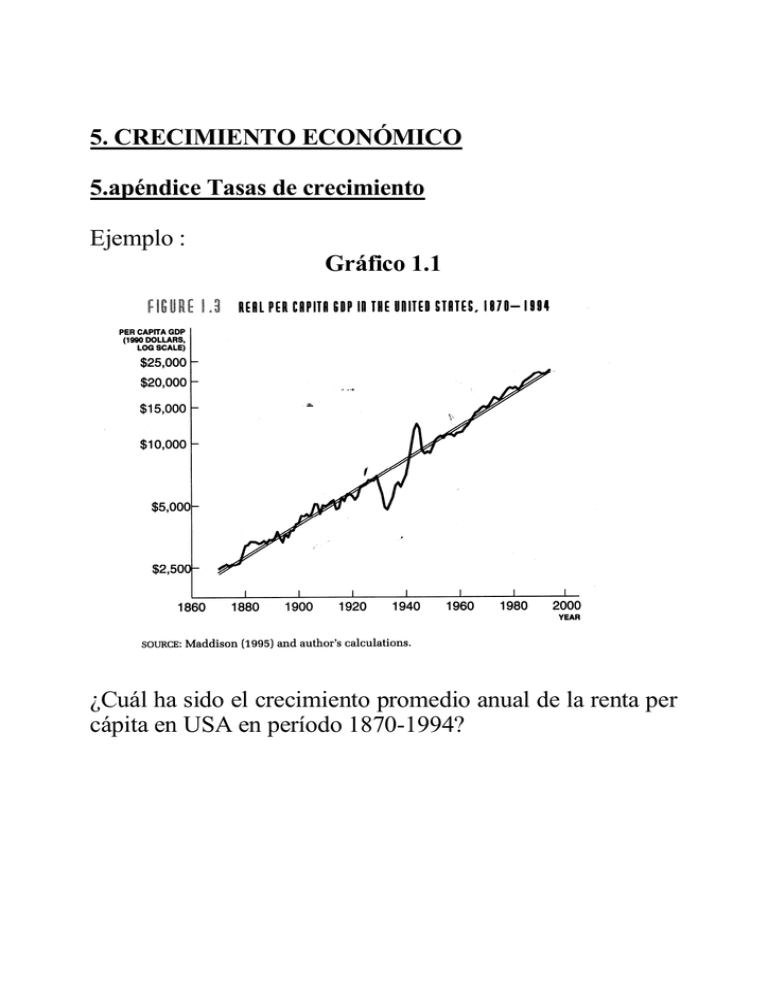
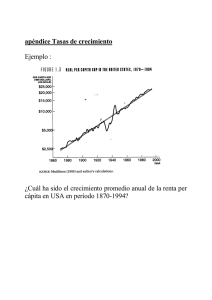
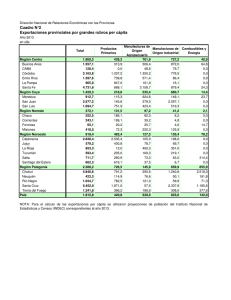
5. CRECIMIENTO ECONÓMICO
5.apéndice Tasas de crecimiento
Ejemplo :
Gráfico 1.1
¿Cuál ha sido el crecimiento promedio anual de la renta per
cápita en USA en período 1870-1994?
Fórmula usual
g x (%) =
x t - x t -1
(∗ 100)
x t -1
x t = x t -1 (1 + g x )
(1.1)
(1.2)
x t 2 − x t1
g x (promedio) =
x t1
Δt
En el ejemplo:
25000 − 2500
2500
g rpc =
= 0.0726 = 7.26 %
124
(1.3)
Tasa anual equivalente
Si x crece todos los años a tasa g x constante:
x t1 +1 = x t1 (1 + g x )
x t1 + 2 = x t1 (1 + g x ) 2
.....
x t 2 = x t1 (1 + g x ) Δt
⎛ x t2
gx = ⎜
⎜ xt
⎝ 1
1/Δt
⎞
⎟
⎟
⎠
-1
En el ejemplo:
1/ 124
⎛ 25000 ⎞
g rpc = ⎜
⎟
2500
⎠
⎝
- 1 = 0.01874 = 1.874 %
(1.4)
Fórmula logarítmica
Si x crece exponencialmente a tasa g x constante:
x = x 0 eg x t
ln x = ln x 0 + g x t
gx =
d(ln x)
dt
(1.5)
(1.6)
(1.7)
Gráficamente, ln (x) = f(t) (escala semilogarítmica) es una
recta de pendiente g x .
Gráfico 1.2
Aplicando (1.5) en t1 y t 2 :
x t1 = x 0 e g x t1
x t2 = x 0 e gxt2
dividiendo miembro a miembro la segunda ecuación por la
primera y tomando logaritmos:
gx =
ln (x t 2 /x t1 )
Δt
(1.8)
En el ejemplo:
ln (25000/250 0)
= 0.01856 = 1.856 %
gx =
124
que es la pendiente de la recta que une los puntos inicial y
final en escala semilogarítmica. Ver gráfico pg. anterior
¿Cuánto tarda x en duplicarse?. Aplicando (1.8):
gx =
Δt =
ln 2
Δt
70
ln 2 0.6931... 69.31...
=
=
≅
g x (%) g x (%)
gx
gx
(1.9)
(1.10)
Tasas de crecimiento de operaciones. Aplicando (1.7) y las
propiedades de los logaritmos:
g (A/B) = g A - g B
(1.11)
g (A×B) = g A + g B
(1.12)
g (Aα ) = α g A ,
para α constante
(1.13)
5.1 Renta per cápita y productividad del trabajo.
Crecimiento económico extensivo e intensivo.
Cuadro 1.1
rpc = y × part
(1.17)
Gráfico 1.3
RPC97 vs. PART
24000
20000
20000
16000
16000
RPC97
RPC97
RPC97 vs. Y97
24000
12000
12000
8000
8000
4000
4000
0
0
0
10000 20000 30000 40000 50000
Y97
.0
.1
.2
.3
.4
.5
.6
.7
PART
Variaciones muy grandes de la renta per cápita ⇐
variaciones muy grandes de la productividad del trabajo y
mucho menores de la tasa de participación en la población
activa (ver graf. pg. siguiente)
⇒ en lo que sigue supondremos generalmente que las
variaciones de la productividad del trabajo vienen
acompañadas de variaciones proporcionales de la renta per
cápita
Crecimiento económico extensivo e intensivo
- crecimiento extensivo: ⇑ proporcional producto (Y),
población (POP), trabajo (L)
⇒ estabilidad renta per cápita (Y/POP), productividad del
trabajo (y = Y/L)
- crecimiento intensivo: ⇑ producto (Y) más que
proporcional a población (POP), trabajo (L)
⇒ ⇑ renta per cápita, productividad del trabajo
Hechos estilizados
- Datos ("hechos estilizados") ⇄ Teorías (modelos)
- Hechos estilizados
- Variación muy grande de los niveles de renta per
cápita y productividad del trabajo entre distintos
países y en el tiempo (cuadro 1.1, gráficos 1.5 y 1.6)
- Importantes variaciones de las tasas de crecimiento
gy entre países (cuadro 1.1)
- Importantes variaciones de las tasas de crecimiento
gy en el tiempo
- gran aceleración desde revolución industrialcientífico-técnica (cuadros 1.2 y 1.3)
- Variaciones de las posiciones relativas entre países:
ricos, pobre, “milagros” y “desastres” (gráfico 1.7)
- Crecimiento "sostenido-equilibrado" en algunos países
(USA...)
- crecimiento sostenido de la productividad y renta per
cápita (gráfico 1.2)
- tendencia estable
- participación en Y de rentas del
- trabajo wL/Y
- capital rK/Y
- relación capital-producto K/Y
- tipo de interés real r (rendimiento del capital)
- Alta correlación crecimiento económico-crecimiento del
comercio internacional (gráfico 1.8)
Gráfico 1.5
Gráfico 1.6
Gráfico 1.7
U.S.A.
1000
Venezuela
U.K.
France
Italy
Mexico
Spain
100
Brazil
Japan
Malaysia
South Korea
Chad
Mozambique
10
Thailand
India
Haiti
Indonesia
Kenya
Nigeria
Uganda
1
1950
China
1960
1970
1980
1990
2000
2010
Ethiopia
Gráfico 1.8