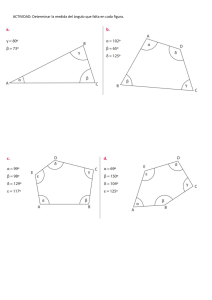
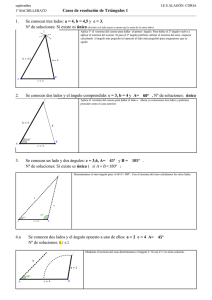
La línea imaginaria que une el punto de observación con un
Anuncio

La línea imaginaria que une el punto de observación con un extremo del lago, junto a la que une el mismo punto con el otro extremo y la que une ambos extremos del lago, forman un triángulo. Conocemos dos de sus lados y la medida del ángulo que forman. Para calcular la medida del otro lado uso el teorema del coseno. El Teorema del coseno nos dice que el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos lados menos el doble producto de estos dos lados por el coseno del ángulo que forman. = + −2 ∗ cos Los lados del triángulo del ejercicio son: =? ; = 145 ; = 215 El ángulo formado por los dos lados que conocemos es de 56º 10’ Sustituyo los datos en la ecuación: = 145 + 215 − 2 ∗ 145 ∗ 215 ∗ cos 56º 10 = 21.025 + 46.225 − 34.715,17 = 32.534,83 = 32.537,83 = 180,37