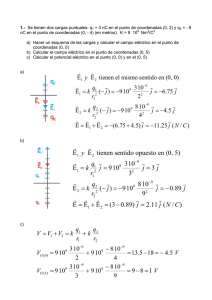
14. Calcula el volumen del sólido limitado superiormente por el

Soluciones:
14. Calcula el volumen del sólido limitado superiormente por el cilindro parabólico z = 1 − y 2 ,
inferiormente por el plano 2x+3y +z +10 = 0 y lateralmente por el cilindro circular x2 +y 2 +x = 0.
Solución: Resolveremos este ejercicio haciendo un cambio de coordenadas.
En primer lugar observamos que el cilindro circular x2 + y 2 + x = 0 se puede escribir como
(x + 21 )2 + y 2 = 14 . Ası́ el centro será en ( −1
, 0) y el radio será 21 .
2
La situación gráfica es la que sigue:
El cambio de coordenadas que utilizaremos:


x = −1/2 + ρ cos(α)
y = ρ sen(α)


z=z
El jacobiano del cambio viene dado por ρ.
Ahora la descripción del conjunto viene dada por:
Ω = {(ρ, α, z) : 0 ≤ ρ ≤ 1/2, 0 ≤ α ≤ 2 π, −10 − 2ρ cos(α) − 3ρsen(α) ≤ z ≤ 1 − ρ2 sen(α)2 }.
y la integral
Z 1/2 Z 2π Z
0
0
1−ρ2 sen(α)2
ρdz dαdρ =
Z
1/2
0
0
−10−2ρ cos(α)−3ρsen(α)
Z
2π
ρ(1 − ρ2 sen(α)2 + 10 + 2ρ cos(α) + 3ρsen(α))dα dz
1/2
π
+ 20π)dρ
2
0
·
¸ 12
ρ2 ρ4 π
= 2π − 3 + 20πρ
2
2
0
1
1
= π( − 7 + 10).
4 2
=
Z
ρ(2 π − ρ2
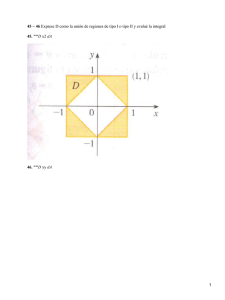
15. Halla el volumen del sólido limitado por los paraboloides de ecuaciones z = 2 − x2 − y 2 y
z = x2 + y 2 .
Solución: Si lo hacemos utilizando coordenadas cartesianas la descripción del conjunto viene
dada por
√
√
Ω = {(x, y, z) ∈ R3 : −1 ≤ x ≤ 1, − 1 − x2 ≤ y ≤ 1 − x2 , x2 + y 2 ≤ z ≤ 2 − x2 − y 2 }
1
Si utilizamos coordenadas cilı́ndricas la descripción serı́a de la forma:
Ω = {(ρ, α, z) : 0 ≤ ρ ≤ 1, 0 ≤ α ≤ 2π, ρ2 ≤ z ≤ 2 − ρ2 }
1
0.5
-0.5-1
0
2
1.5
1
0.5
1
0.5
0
Utilizaremos las coordenadas cilı́ndricas:
Z
Z 1 Z 2π Z 2−ρ2
ρdz dα, dρ =
V =
0
ρ2
0
1
=
Z
0
0
Z
0
-0.5
1
-1
2π
2(ρ − ρ3 )dαdρ
ρ2 ρ4
4π(ρ − ρ )dρ = 4π
−
2
4
3
0
·
¸1
=π
0
x−y
16. Calcula la integral de la función f (x, y) = e x+y sobre el triángulo limitado por los ejes de
coordenadas y la recta x + y = 1.
Solución: Para hacer este ejercicio recurriremos de nuevo al cambio de coordenadas en este caso
llamamos u = x − y y v = x + y. (Ejercicio: Comprobar que efectivamente es un cambio de
coordenadas (aplicación biyectiva de clase C 1 y con determinante jacobiano distinto de cero))
J(φ(x, y)) =
1 −1
=2
1 1
Ası́ el determinante del cambio de coordenadas es 21 .
El triángulo limitado por los ejes y la recta x + y = 1 se transforma ahora de la forma que sigue:
Recta y = 0 cuando x ∈ [0, 1] ⇒ u = v cuando v ∈ [0, 1].
Recta x = 0 cuando y ∈ [0, 1] ⇒ u = −v cuando v ∈ [0, 1].
Recta x + y = 1 ⇒ v = 1
Ahora la integral queda de la forma:
Z
0
1
Z
v
−v
Z
1 u/v
1 1 u/v v
ve ]−v du
e dudv =
2
2 0
Z
1 1
1
=
v(e−1 − e)dv = (e−1 − e)
2 0
4
2
1
6
¾
u
-
1
¾
v
-
1
?
?
17. Utiliza el teorema del cambio de variable para determinar el valor de la integral
Z
R
−R
Z
√
−
R2 −x2
√
log(1 + x2 + y 2 )dydx
R2 −x2
con R > 0.
Solución: Utilizamos el cambio a coordenadas polares. El conjunto sobre el cual estamos integrando es una circunferencia de centro (0, 0) y radio R.
En coordenadas polares la descripción del conjunto viene dada por
Ω = {(ρ, α) : 0 ≤ ρ ≤ R, 0 ≤ α ≤ 2π}
Z
0
R
Z
0
2π
2
Z
R
Z
ρ log(1 + ρ )dα dρ = 2π
ρ log(1 + ρ2 )dρ
0
¤R
£
= π (1 + ρ2 ) log(1 + ρ2 ) − 1 − ρ2 0 = π((1 + R2 ) log(1 + R2 ) − R2 )
18.- Sea D el elipsoide de revolución de ecuación
D = {(x, y, z) ∈ R3 :
x2 y 2 z 2
+ 2 + 2 = 1}
a2
b
c
con a, b, c constantes positivas.
(a) Comprueba que la aplicación φ : R3 → R3 , dada por
φ(u, v, w) = (au, bv, cw)
es un cambio de variable. (Ejercicio)
3
(b) Utiliza el resultado anterior para calcular el valor de la integral.
Z r
x2 y 2 z 2
1 − 2 − 2 − 2 dxdydz
a
b
c
D
Solución: El jacobiano del cambio de variable es abc. Ahora la integral original queda de la forma:
Z
D
Z
√
2
2
2
abc 1 − u − v − w dudvdw = abc
1
0
= 4π abc
2π
Z
Z
0
1
0
= 1 4π abc
Z
Z
π
0
p
ρ2 sen(β) 1 − ρ2 dβdαdρ
p
ρ2 1 − ρ2 dρ
π/2
sen2 (t) cos2 (t)dt
0
= abc
π2
4
19. Sea Ω ⊂ R3 una región acotada, de forma que la densidad en cada punto Ω viene dada por
ρ(x). El centro de masas de Ω se define como un punto x = (x1 , x2 , x3 ) de forma que:
Z
1
xi =
· xi δ(x1 , x2 , x3 ) dx1 dx2 dx3 , i = 1, 2, 3.
M asa Ω
Calcula el centro de masas de un cono de altura h y radio de la base igual a r cuando:
1. La densidad es constante.
2. La densidad en cada punto es proporcional a la distancia a la base.
3. ρ(x1 , x2 , x3 ) = 1 + x21 + x22
Solución: El cono en coordenadas cilı́ndricas viene descrito de la forma:
Ω = {(ρ, α, z) : 0 ≤ ρ ≤ r, 0 ≤ α ≤ 2π,
4
h
ρ ≤ z ≤ h}
r
1. Supongamos que la densidad δ es constante.
Z r Z 2π Z h
1
ρ2 cos(α)δdz dα dρ = 0
x1 =
h
M asa 0 0
ρ
r
Z r Z 2π Z h
1
ρ2 sen(α)δdz dα dρ = 0
x2 =
h
M asa 0 0
ρ
r
Z r Z 2π Z h
1
ρzδdz dα dρ
x3 =
h
M asa 0 0
ρ
r
Z r
1
ρ3
=
h2 (ρ − 2 )dρ
δπ
M asa
r
0
¸
· 2
4 r
ρ
1
2 ρ
δπh
− 2
=
M asa
2
4r 0
2
1
r
=
δπ h2
M asa
4
2
).
Por otra parte, M asa = δπr3 ·h . Ası́, el centro de masas será el punto de coordenadas C = (0, 0, 3h
4
p
2
2
2
2. Observación: En este caso suponemos δ(x, y, z) = K · x + y + z , siendo K una constante.
El procedimiento es el mismo que en el caso anterior.
5