carga y descarga de un condensador

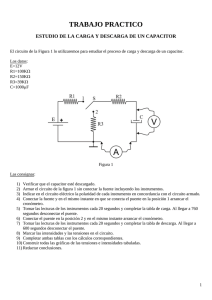
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARÍA
CAMPUS SANTIAGO
LABORATORIO FIS 119 / FIS 120
PRIMER SEMESTRE 2010
CARGA Y DESCARGA DE UN CONDENSADOR
Introducción

Donde
Marco Teórico.

= R*C
La capacidad eléctrica C se define como:
La caída de tensión en el capacitor como
función del tiempo es:
Q
V
VC (t )  V0 (1  e t /  )
C
(1.1)
Se interpreta como la capacidad de los
cuerpos de almacenar carga eléctrica. La unidad de
la capacidad eléctrica es el
farad y depende
exclusivamente de la geométrica del cuerpo.
1 farad 
1Coulomb
Volt
C=
0
A
d
Para un capacitor inicialmente cargado se
puede descarga por medio de una resistencia R
según la figura 2, entonces la carga en las placas
diminuye como:
(1.2)
El dispositivo que almacena carga
denomina capacitor, y el mas simple es el
placas paralelas, entonces la capacidad sera:
(1.5)
Q(t )  Q0 e t / 
(1.6)
se
de
(1.3)
Donde:
A
d
0
Figura 2 Circuito simplificado de descarga de
un capacitor.
= área de las placas
= separación entre placas
= permisividad eléctrica del vacío
Y la tensión en el capacitor será:
Cuando un capacitor de placa paralelas
inicialmente descargado se conecta a una FEM por
medio de una resistencia R, se establece una
corriente eléctrica en el circuito que cesa cuando la
caída de tensión entre las placas es igual a la FEM
aquí el capacitor queda cargado como lo muestra la
figura 1.
VC (t )  V0 e t / 
El tiempo que el circuito RC demora en
disminuir a la mitad de su tensión inicial se relaciona
como:
t1/2 =  ln(2)
Figura 1 condensador de placas paralelas
El tiempo de carga de un capacitor depende
del valor del capacitor y de la resistencia del circuito.
Entonces las placas del capacitor se cargarán como:
(1.4)
t /
Q(t )  Q0 (1  e
(1.7)
)
Página 1 de 3
(1.8)
La conexión inversa del condensador los puede dañar e
incluso producir su destrucción, adicionalmente pierde la
capacidad de carga dada en la ecuación 1.4, comportándose
erráticamente.

Figura 3 Método de media amplitud para el
cálculo del
.
Esta expresión es útil para determinar  a
partir de una gráfica Vc(t). Y es conocido como
“método de media amplitud”.
Observación directa de la carga y descarga
de un capacitor.
Se debe implementar el circuito de la figura 5, se debe
obtener las gráficas del proceso de carga y descarga, usando
un voltímetro y un cronómetro, para posteriormente realizar
el análisis utilizando el ajuste propio del Excel y el método
de media amplitud, luego se comparan ambos métodos con
las predicciones teóricas, además se debe entregar el valor
de la constante de carga (tau) de ambos métodos.
Resnick, sección 31-2, 31-3, 33-7
Sears, sección 24.1, 24.2, 26.4
100 K
3V

Objetivos:




V
470µF
Determinar la influencia de la capacidad de un
condensador en los procesos de carga y descarga.
Familiarizar al estudiante con el uso de
instrumentos para realizar mediciones eléctricas.
Medir la resistencia interna de un instrumento.
Caracterizar y determinar la capacidad en paralelo
y serie.
Figura 5 Circuito a implementar para la carga y descarga de
un capacitor.

Obtención de la resistencia interna de un
voltímetro.
Desarrollo Experimental
Se debe tener presente una serie de indicaciones y
precauciones par realizar la presente experiencia:
Los condensadores electrolíticos como los ocupados en esta
experiencia poseen polaridad, por lo cual, se debe tener la
precaución de conectarlos bien generalmente el pin negativo
posee una marca ( - - ) según lo apreciado en la figura 4.
Se implementa el circuito de la figura 6, observe que tanto
la fuente como el capacitor están en paralelo al voltímetro,
se debe cargar el condensador hasta que alcance el voltaje
de la fuente, posteriormente se retira la conexión de la
fuente dejando solo el capacitor y el instrumento conectado,
el capacitor comenzará a descargarse a través de la
resistencia interna del instrumento, utilizando el método de
media amplitud se puede calcular el tau, para posteriormente
obtener el valor de la resistencia interna del instrumento,
los resultados obtenidos deben ser analizados y comparados
con las predicciones teóricas.
Figura 4 Condensador electrolítico.
Página 2 de 3

4,7uF
Figura 6 Medición de la resistencia interna del voltímetro.

dos
Observación directa de la carga y descarga
de un capacitor asistida por computador.
Se debe implementar el circuito de la figura 7 y obtener una
gráfica del voltaje del capacitor en función del tiempo, para
los procesos de carga y descarga, para ello se utilizará el
software del multimetro GDM-396, el cual permite capturar
los datos hacia el computador.
Se realiza un análisis de los datos, se obtiene la ecuación
empírica del gráfico de descarga y se compara con las
predicciones teóricas.
100 K
Bibliografía
Resnick, Halliday, Krane, Física Volumen 2, cuarta
edición.
Sears, Zemansky, young, Freedman,
Universitaria Tomo 2, Décimo primera edición.
v
3V
100µF
Figura 7 Circuito a implementar para el estudio de la carga y
descarga asistida por computador.

de
Se modifica el circuito de la figura 7, conectando una
resistencia de 100 KΩ en paralelo a la que ya está
conectada, y reemplazando el capacitor por uno de 470 μF,
se obtiene nuevamente una gráfica del voltaje del capacitor
en función del tiempo, para la descarga. Se realiza un
análisis de los datos, se obtiene la ecuación empírica del
gráfico de descarga y se compara con las predicciones
teóricas, también debe compararse el tau con el obtenido en
el punto anterior, y analizar el efecto de la resistencia en
paralelo.
v
3V
Estudio del comportamiento
resistencias en paralelo.
Estudio del comportamiento
capacitares en serie.
de
dos
Se modifica el circuito de la figura 7, se retira el capacitor
de 100 μF y en su lugar se conectan 2 capacitores de 470 μF
en serie, se obtiene nuevamente una gráfica del voltaje del
capacitor en función del tiempo, para la descarga. Se realiza
un análisis de los datos, se obtiene la ecuación empírica del
gráfico de descarga y se compara con las predicciones
teóricas, también debe compararse el tau con el obtenido en
el punto anterior, y analizar el efecto de la capacidad en
serie.
Página 3 de 3
Física