FUNCIONES Y GRÁFICAS 1. La siguiente gráfica corresponde al

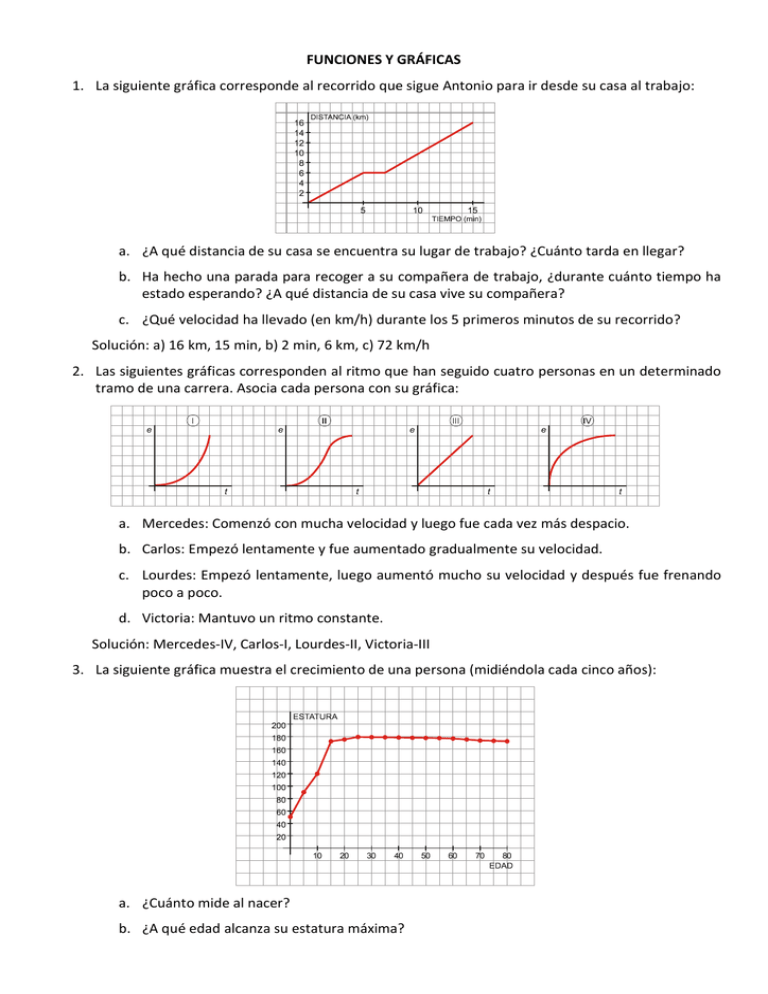
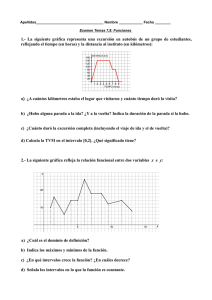
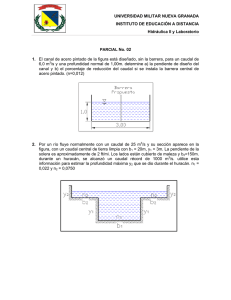
FUNCIONES Y GRÁFICAS
1. La siguiente gráfica corresponde al recorrido que sigue Antonio para ir desde su casa al trabajo:
a. ¿A qué distancia de su casa se encuentra su lugar de trabajo? ¿Cuánto tarda en llegar?
b. Ha hecho una parada para recoger a su compañera de trabajo, ¿durante cuánto tiempo ha
estado esperando? ¿A qué distancia de su casa vive su compañera?
c. ¿Qué velocidad ha llevado (en km/h) durante los 5 primeros minutos de su recorrido?
Solución: a) 16 km, 15 min, b) 2 min, 6 km, c) 72 km/h
2. Las siguientes gráficas corresponden al ritmo que han seguido cuatro personas en un determinado
tramo de una carrera. Asocia cada persona con su gráfica:
a. Mercedes: Comenzó con mucha velocidad y luego fue cada vez más despacio.
b. Carlos: Empezó lentamente y fue aumentado gradualmente su velocidad.
c. Lourdes: Empezó lentamente, luego aumentó mucho su velocidad y después fue frenando
poco a poco.
d. Victoria: Mantuvo un ritmo constante.
Solución: Mercedes-IV, Carlos-I, Lourdes-II, Victoria-III
3. La siguiente gráfica muestra el crecimiento de una persona (midiéndola cada cinco años):
a. ¿Cuánto mide al nacer?
b. ¿A qué edad alcanza su estatura máxima?
c. ¿Cuándo crece más rápido?
d. ¿Cuál es el dominio?
e. ¿Por qué hemos podido unir los puntos?
Solución: a) 55 cm, b) a los 25, c) de los 10 a los 20 años, d) Dom(f)=[0, 80], e) porque la edad es
una variable continua.
4. Construye una gráfica correspondiente al caudal de agua de un río durante un año, sabiendo que:
En enero, el caudal era de 40 hm3 y fue aumentando hasta el mes de abril cuyo caudal era de 60
hm3. En abril el río tenía el máximo caudal del año. A partir de este momento, el caudal fue
disminuyendo hasta que, en agosto, alcanzó su mínimo, 10 hm3. Desde ese momento hasta finales
de año, el caudal fue aumentando. En diciembre, el caudal era, aproximadamente, el mismo que
cuando comenzó el año.
Solución:
5. ¿Cuáles de las siguientes expresiones analíticas corresponden a cada una de las dos gráficas dadas?
1) y 
x
2
3) y  x 2  2
2) y  2 x
4) y  x 2
Solución: a) 2, b) 4
6. Dada la función y 
2
, escribe tres valores que pertenezcan al dominio de definición de la
x 1
función y otros tres que no pertenezcan.
Solución: 2, 3 y 4
7. Cierto jardín se abastece de agua a través de un pozo que se llena y se vacía automáticamente,
según la siguiente gráfica:
a. ¿Cuál es el periodo de la función?
b. ¿Cuánto tarda en llenarse el pozo? ¿Y en vaciarse?
c. ¿En qué momentos el pozo tiene 2 m3 de agua?
d. ¿Qué volumen de agua hay después de 3 horas?
Solución: a) 6 h, b) 4’5 h, 1’5 h, c) 2 h, 5 h, 8h, 11h,…d) 3 m3
8. Se va a organizar una excursión y el precio por persona va a depender del número de personas que
vayan a dicha excursión. El número máximo de plazas es de 60, y el mínimo, 10, admitiendo
solamente grupos de 10 personas. La siguiente gráfica nos muestra la situación:
a. ¿Qué significado tiene el punto (20, 8)? ¿Y el (40, 4)?
b. ¿Por qué hemos dibujado la gráfica solo entre 10 y 60? ¿Podríamos continuarla?
c. ¿Es una función continua o discontinua?
d. ¿Por qué no unimos los puntos?
Solución: a) 20 plazas y 8 € cada persona, 40 plazas y 4 € por persona, b) porque hay un mínimo
de 10 personas y un máximo de 60, no podríamos continuarla, c) es discontinua, d) porque el
número de plazas es un número natural.
9. Dependiendo del día de la semana, Rosa va al instituto de una forma distinta:





El lunes va en bicicleta.
El martes, con su madre en el coche (parando a recoger a su amigo Luis).
El miércoles, en autobús (que hace varias paradas).
El jueves va andando.
Y el viernes, en motocicleta.
a. Identifica a qué día de la semana le corresponde cada gráfica:
b. ¿Qué día tarda menos en llegar? ¿Cuál tarda más?
c. ¿Qué día recorre más distancia? Razona tu respuesta.
Solución:a) I-Jueves, II-Viernes, III-Miércoles, IV-Martes, V-Lunes, b) Viernes, Jueves, c) La
misma porque hay la misma distancia de su casa al instituto independientemente del trasporte
que utilice.
10. La siguiente gráfica nos da el valor del área de un rectángulo de 20 cm de perímetro en función de
su altura:
a. ¿Cuál es el dominio de la función?
b. Indica los tramos en los que la función es creciente y en los que es decreciente.
c. ¿En qué valor se alcanza el máximo? ¿Cuánto vale dicho máximo? ¿Qué figura geométrica
es la que tiene esas medidas?
Solución: a) Dom (f)=[0,10], b) Creciente: (0,5), Decreciente: (5,10), c) x = 5 y f(x)=25, es una
parábola.
11. Construye una gráfica que corresponda a la audiencia de una determinada cadena de televisión
durante un día, sabiendo que:
A las 0 horas había, aproximadamente, 0,5 millones de espectadores. Este número se mantuvo
prácticamente igual hasta las 6 de la mañana. A las 7 de la mañana alcanzó la cifra de 1,5 millones
de espectadores. La audiencia descendió de nuevo hasta que, a las 13 horas, había 1 millón de
espectadores. Fue aumentando hasta las 21 horas, momento en el que alcanzó el máximo: 6,5
millones de espectadores. A partir de ese momento, la audiencia fue descendiendo hasta las 0
horas, que vuelve a haber, aproximadamente, 0,5 millones de espectadores.
Solución:
12. Asocia cada gráfica con su expresión analítica:
a) y  x
b) y  x 2
c) y  x  1
Solución: a-III, b-I, c-II, d-IV
d) y  x 2  1
13. Dibuja una función continua con dominio de -3 a 4, que tenga un máximo en (0, 5) y un mínimo en
(2, -3).
Solución: respuesta libre
14. Escribe la expresión analítica, A(x), del área de un triángulo isósceles en el que uno de los lados
iguales mide x y el desigual 6 cm. Después, dando valores a x, representa la gráfica de la función
A(x). ¿Cuál es su dominio de definición?
Solución: A( x)  3  x 2  9 , Domf (x)   ,3  3,  
15. El consumo de agua en un colegio viene dado por esta gráfica:
a. ¿Durante qué horas el consumo de agua es nulo? ¿Por qué?
b. ¿A qué horas se consume más agua? ¿Cómo puedes explicar esos puntos?
c. ¿Qué horario tiene el colegio?
d. ¿Por qué en el eje X solo consideramos valores entre 0 y 24? ¿Qué significado tiene?
Solución: a) Desde las 0 h hasta las 8 h y desde las 18 h hasta las 24 h porque el colegio está
cerrado y no hay consumo, b) a las 12 h y a las 16 h porque son los recreos y hay más consumo,
c) de 8 h a 18 h, d) es un día entero.
16. La velocidad de un móvil en función del tiempo que tarda en recorrer 1 km viene dada por la
siguiente gráfica:
a. ¿Es una función creciente o decreciente?
b. ¿Cuál es la velocidad cuando t = 1 hora?
c. ¿Y cuando t = 2 horas?
d. ¿Y cuando t = 15 minutos?
e. Al aumentar el tiempo, ¿a qué valor tiende la velocidad?
Solución: a) decreciente, b) 1 km/h, c) 0’5 km/h, d) 3 km/h, e) la velocidad tiende a cero
17. La siguiente gráfica refleja la relación funcional entre dos variables x e y:
a. ¿Cuál es el dominio de definición?
b. Indica los máximos y mínimos de la función.
c. ¿En qué intervalos crece la función? ¿En cuáles decrece?
d. Señala los intervalos en lo que la función es constante.
Solución: a) [1,13], b) Máximos: A(1’5,16), B(6,26), C(11’5,14), Mínimos: D(1,10), E(3,6),
F(9’5,12),
G(13,8),
c)
Creciente:
(1,1’5)U(3,4)U(5,6)U(9’5,11’5),
Decreciente:
(1’5,3)U(6,7)U(8’5,9’5)U(11’5,13), d) Constante: (4,5)U(7,8’5)
18. Observa la siguiente gráfica:
a. ¿Es una función periódica?
b. ¿Cuál es el periodo?
c. Calcula f (0’5) y f (8).
Solución: a) Sí, b) T=5, c) f(0’5)=2, f(8)=f(3)=2
19. Escribe en función de x el área de la parte coloreada del siguiente cuadrado de lado 8 cm.
Solución: A( x)  2 x 2  x  64
20. La siguiente gráfica representa una excursión en autobús de un grupo de estudiantes, reflejando el
tiempo (en horas) y la distancia al instituto (en kilómetros):
a. ¿A cuántos kilómetros estaba el lugar que visitaron?
b. ¿Cuánto tiempo duró la visita al lugar?
c. ¿Hubo alguna parada a la ida? ¿Y a la vuelta?
d. ¿Cuánto duró la excursión completa (incluyendo el viaje de ida y el de vuelta)?
Solución: a) 140 km, b) 4 h, c) No, a la vuelta hubo una parada de 1 h, d) 9h
21. Asocia cada enunciado con la gráfica que le corresponde:
a. Altura de una pelota que bota, al pasar el tiempo.
b. Coste de una llamada telefónica en función de su duración.
c. Distancia a casa durante un paseo de 30 minutos.
d. Nivel del agua en una piscina vacía al llenarla.
Solución: a-II, b-III, c-IV, d-I
22. La gráfica informa de la evolución del saldo de la cuenta bancaria de Marisa a lo largo de un año:
a. ¿Con qué saldo comenzó el año?
b. ¿Cuál es el sueldo mensual de Marisa?
c. ¿En qué momento tuvo mayor saldo en la cuenta? ¿A cuánto ascendía?
d. En junio, Marisa hizo un viaje, ¿cuánto le costó? ¿Cuánto le prestó el banco?
e. ¿Cuánto gastó en agosto?
f. ¿Cuánto ahorró en octubre?
g. ¿En qué mes liquidó la deuda que tenía con el banco?
Solución: a) 1250 €, b) 1500 €, c) a principios de Abril 3000 €, d) 4000 €, el banco le prestó 1750
€, e) 750 €, f) 250 €, g) A finales de Septiembre liquida totalmente la deuda.