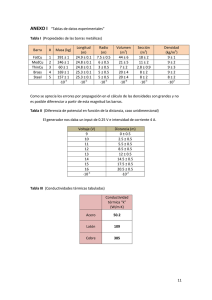
1. Determinar la Carga máxima. σe= 173.3 MPa γ=2 b= 40 mm t= 4

1. Determinar la Carga máxima.
σe= 173.3 MPa
γ=2
b= 40 mm
t= 4 mm
L = 225 mm
bσu=σe/γ= 86.65 MPa
= 410.8 N
2. Determinar para un montaje de ¼ de puente y ½ puente y para distintos estados de
carga (0.5, 1.0 y 1.5 Kg) los siguientes parámetros:
▪ ε : Deformación longitudinal
▪ σ : Tensión
▪ Gráfica tensión vs. deformación (ε – σ)
▪ E : módulo de elasticidad y compararlo con el del
ξ
material.
▪ Comparar el módulo de elasticidad con el arriba
facilitado.
▪ ε : Deformación longitudinal
Para obtener la ε se necesita un factor de conversión mediante el que pasar el
voltaje, proporcionado por las galgas, a deformaciones. Dicho factor lo obtenemos
mediante la resistencia de calibración, que nos dará un valor determinado. Bajo las
hipótesis de pequeñas deformaciones y material isótropo y lineal, se puede trazar
una recta que, pasando por el origen, cruce por el punto de calibración. Una vez se
tiene esta recta ya se puede referir los voltajes a sus correspondientes
deformaciones.
A continuación se muestran los datos necesarios para dibujar la recta:
Rc=29880
Rg=120
K=2.1
Vcalibración=1748mV
Haciendo uso de las siguientes operaciones, obtenemos las
= 1.9040*10-3
Proporción

En la imagen inferior se puede apreciar esta recta:
Patrón de calibración
2000
1800
y = 917700x
1600
Voltaje (mV)
1400
1200
1000
800
600
400
200
0
0,0000
0,0005
0,0010
0,0015
0,0020
ε (mm/mm)
▪ σ : Tensión
Para obtener la σ simplemente se ha usado la fórmula:
A continuación se recopilan los datos hasta ahora encontrados:
Cargas (kg)
V (mV)
ε (10-3)
σ (MPa)
Cargas (kg)
V/2 (mV)
ε (10-3)
σ (MPa)
¼ Puente longitudinal
0.5
1
127
258
0.1384
0.2812
10.35
20.69
1.5
388
0.4228
31.04
½ Puente longitudinal
0.5
1
125
254.5
0.1362
0.2774
10.35
20.69
1.5
384.5
0.4190
31.04
▪ Gráfica tensión vs. deformación (ε – σ)
1/4 Puente Longitudinal
35
y = 72,758x + 0,2644
R² = 1
30
σ (MPa)
25
20
15
10
5
0
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
ε ·10-3 (mm/mm)
1/2 Puente Longitudinal
35
y = 73,179x + 0,3854
R² = 1
30
σ (MPa)
25
20
15
10
5
0
0
0,05
0,1
0,15
0,2
0,25
0,3
ε ·10-3 (mm/mm)
▪ Eξ : módulo de elasticidad y compararlo con el del material.
Regresión ¼ : σ=72.758ε*10-3+0.2644  E1/4=72.8GPa
Regresión ½ : σ=73.179ε*10-3+0.3854  E1/4=73.2GPa
0,35
0,4
0,45
Valores comunes para el aluminio son: 63≤E≤70.
Para esta aleación: 57≤E≤75.
3. Comparar los resultados obtenidos en los dos montajes y en el caso
de presentarse diferencias importantes justificarlas.
El valor obtenido del módulo de Young para ambos métodos (1/4 y 1/2 de puente)
difieren en 0.4 GPa. El ½ puente es más preciso, puesto que hace el promedio
entre un ensayo de tracción (cara superior) y otro a compresión (cara inferior).
Ambos valores entran en el rango teórico dado.
4. Determinar para las cargas (0.5, 1.0 y 1.5 Kg) y en montaje de ¼ de puente el
coeficiente de Poisson.
¼ Puente transversal
0.5
1
40
80
0.0436
0.0872
0.315
0.310
Cargas (kg)
V (mV)
ε (10-3)
ν
1.5
121
0.1319
0.312
5. Con la probeta que tiene instalada la roseta rectangular y para una carga de 1 Kg
determinar:
▪ ε
long
: Deformación en la dirección longitudinal de la
probeta
▪ Deformaciones principales
▪ Coeficiente de Poisson.
▪ Tensiones principales
▪ Direcciones principales.
▪ Tensión equivalente y coeficiente de seguridad.
▪ Contrastar las tensiones y deformaciones principales
obtenidas con las teóricas.
βa=122˚
βb=77˚
βc=32˚
Esquema de la colocación de la roseta
▪ εlong : Deformación en la dirección longitudinal de la probeta
Roseta
V (mV)
ε (10-3)
a
189
0.2060
b
280
0.3051
c
16
0.0174
Usando el sistema de ecuaciones:
Se obtiene que, para 1 Kg:
ε xx=-0.1035*10-3
ε yy=0.3269*10-3
ε xy=0.714*10-8
La deformación en la dirección longitudinal es ε yy=0.3269*10-3.
▪ Deformaciones principales
Puesto que la ε xy es muy pequeña se puede aproximar a 0 y consecuentemente las
deformaciones principales son:
ε I=-0.1035*10-3
ε II=0.3269*10-3
▪ Coeficiente de Poisson.
El coeficiente de Poisson obtenido en este apartado se ajusta a los valores teóricos
de la cuestión 2.
▪ Tensiones principales
Aplicando la ley de Hooke matricial, y partiendo de las deformaciones principales ya
encontradas:
σI=10.18MPa
σII=33.86MPa
σIII=15.87MPa
Donde se ha usado el módulo de Young de ½ de puente puesto que es más preciso
(E=73.2 GPa) y el coeficiente de Poisson de 0.33.
▪ Direcciones principales.
En este estado coinciden, debido a la aproximación mencionada, con las direcciones
x e y dibujadas.
▪ Tensión equivalente y coeficiente de seguridad.
Se ha decidido aplicar el criterio de Von Mises debido a los buenos resultados que
da.
Se obtiene:
El factor de seguridad lo obtenemos mediante la fórmula:
▪ Contrastar las tensiones y deformaciones principales obtenidas con las teóricas.
A continuación se tratará únicamente el caso de 1Kg, puesto que el resto de casos
se lograrían siguiendo el mismo método.
Aplicando la fórmula del guión:
Obtenemos que la
teórica:
Mientras que la obtenida mediante galgas (en la dirección principal coincidente con
el eje y):
La deformación teórica:
La deformación experimental(en la dirección principal coincidente con el eje y):
ε experimental=0.003269
Se aprecia que los valores teóricos distan bastante de los experimentales, esto
puede estar provocado por diversos motivos: inexactitud de los elementos de
medición, falta de experiencia en el uso de dichos elementos y/o errores de
aproximación.
6. Conclusiones de cada tipo de ensayo.
El ensayo con las galgas extenso-métricas en posición longitudinal a ¼ y ½ de puente nos han
permitido encontrar el módulo elástico (E) del material. Hay que tener en cuenta que aunque
pequeñas, se presentan diferencias entre ambos casos, ya que para el ½ puente hay una galga
que se solicita a tracción mientras que la otra es a compresión. Eso hay que tenerlo en cuenta
a la hora de hacer el conexionado puesto que conectar ambas galgas en posiciones opuestas
(son opuestas las posiciones 1 con 3, y 2 con 4 en el puente de Wheatstone) daría un resultado
erróneo, al compensarse una elongación con la otra, siendo el conexionado correcto aquél
donde ambas aportaciones se sumen. Los valores que se obtengan en el voltímetro indicarán
pues el doble del voltaje que nosotros queremos y dividiendo por dos habremos hecho una
media de la elongación de las fibras superiores y las fibras inferiores.
Con las galgas instaladas en posición transversal podremos encontrar el valor del coeficiente
de Poisson, ya que obtenemos las deformaciones transversales. Dividiendo estas por las
longitudinales obtenemos dicho factor con una precisión sorprendente.
Con la roseta podemos obtener el alargamiento en 3 direcciones diferentes, pudiendo
establecer una relación entre estos, y los que se darían en las direcciones principales, así como
también dichas direcciones, y las tensiones.
Es importante remarcar el papel que juega la resistencia de calibración. Nos permite, una vez
consideramos que nuestro estado está en 0, obtener un alargamiento ficticio que nos
permitirá establecer el patrón de calibración. Como nuestro problema es lineal consideramos
que obedecerá a una recta cuyo origen de deformaciones será el origen de tensiones (a
tensión nula, deformación nula). Dicha recta nos permitirá traducir las lecturas de voltaje a
mesuras de alargamiento. Como el voltaje de calibración es muy similar en todos los
experimentos hemos considerado que el patrón de calibración será siempre el mismo. Una vez
encontrado la expresión de la recta es la misma que aplicamos para toda la práctica.