Ejemplos de preguntas del examen teórico de Introducción a la

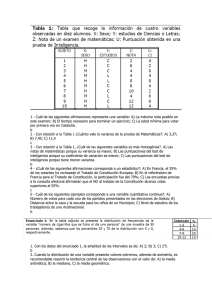
Ejemplos de preguntas del examen teórico de Introducción a la Psicometría.
NOTAS SOBRE EL EXAMEN TEÓRICO:
EN EL EXAMEN TEÓRICO NO SE PUEDE UTILIZAR CALCULADORA
NO SE PUEDEN UTILIZAR APUNTES
LOS ERRORES DESCUENTAN (POR CADA 2 ERRORES SE DESCUENTA UN ACIERTO)
1. Indique cual de los siguientes supuestos NO es un supuesto de la teoría clásica de los tests:
a. La correlación entre las puntuaciones verdaderas de un test y los errores de otro test ha de
ser cero.
b. La correlación entre los errores de un test y los errores de otro test ha de ser cero.
c. La correlación entre las puntuaciones verdaderas en un test y las verdaderas en otro test ha
de ser cero.
2. Al unir 2 pruebas paralelas en una única prueba, podemos decir que:
a. se incrementara la varianza de las puntuaciones verdaderas y se reducirá la varianza error.
b. se mantendrá la varianza de las puntuaciones verdaderas pero se reducirá la varianza error.
c. se incrementará la varianza de las puntuaciones verdaderas y la varianza error.
3. Aplicamos el modelo logístico de 2 parámetros a dos ítems y obtenemos a 1= 2 y b1 = 0, y a2 =
2.4 y b2 = -1.6
a. El ítem 1 es más fácil y discriminativo que el 2.
b. El ítem 1 es más difícil y menos discriminativo que el 2.
c. Ambos ítems tienen una discriminación media.
4. En la siguiente tabla aparecen los indicadores H y HC del mismo ítem con respecto a un test
de 5 ítems, con respecto al test alargado hasta 10 ítems y con respecto al test alargado hasta 20
ítems:
H
HC
Test 1 .624 .100
Test 2 .420 .413
Test 3 .560 .460
¿Cuál de las siguientes alternativas refleja el orden de los tests, de mayor a menor longitud?
a. 3, 2 y 1
b. 1, 3 y 2
c. 2, 3 y 1
5. El coeficiente de fiabilidad de una prueba es 0.6 y su varianza 10, esto quiere decir que:
a. El 64% de la varianza de las puntuaciones en el test es varianza error.
b. La varianza de los errores es 4
c. La varianza de las puntuaciones verdaderas es 3.6
6. Al hacer un análisis factorial sobre 4 ítems, obtenemos que los ítems saturan en el primer
factor rotado 0.6,-0.5, 0.2 y 0.1 y saturan en el segundo factor rotado, 0.1, 0.5, 0.5 y 0.6. Para
interpretar el significado de ambos factores sería necesario considerar los ítems:
a. 1 y 2 (para interpretar el factor 1) y 2, 3 y 4 (para interpretar el factor 2)
b. 1 (para interpretar el factor 1) y 2, 3 y 4 (para interpretar el factor 2)
c. 1 (para interpretar el factor 1) y 3 y 4 (para interpretar el factor 2)
7. La siguiente gráfica representa el incremento de las varianzas de un test (varianza de las
puntuaciones verdaderas, varianza de los errores y varianza de las puntuaciones empíricas)
según se añaden formas paralelas a un test.
160
Varianza
140
1
2
E
120
100
80
X
60
40
V
20
3
0
1
2
3
4
5n
E: error
X: Puntuación empírica
V: Puntuación verdadera
El crecimiento de la varianza de los errores se muestra con la línea:
a. 1
b. 2
c. 3
8. Dos personas responden al mismo test y sus puntuaciones son 36 y 42. Hacemos el oportuno
contraste estadístico y rechazamos (no podemos mantener) la hipótesis nula de igualdad de
puntuaciones verdaderas. Esto significa que:
a. De tener el test un error típico menor, también hubiésemos rechazado la hipótesis nula.
b. De tener el test un error típico mayor, también hubiésemos rechazado la hipótesis nula.
c. El error típico no afecta a la decisión del contraste.
9. Al realizar un análisis factorial observamos que la solución de un factor se ajusta a los datos.
Al añadir ítems paralelos a los ya presentes, es esperable que:
a. la proporción de varianza explicada por el factor aumente
b. la proporción de varianza explicada por el factor no cambie
c. la proporción de varianza explicada por el factor disminuya
10. En un análisis factorial de los 5 ítems de un test, obtenemos que los ítems saturan en un
factor. A continuación aparece la matriz de componentes:
Factor
Ítem 1 0.2
Ítem 2 0.4
Ítem 3 0.4
Ítem 4 0.6
Item 5 0.5
Según el modelo factorial los ítems que más correlacionan entre sí son:
a. el 1 y el 3
b. el 2 y el 3
b. el 4 y el 5
11. Las puntuaciones de un test siguen la distribución normal. Juan obtiene una puntuación de
zn = 1, Mariana una puntuación Tn = 75 y Pedro tiene una puntuación Dn = 90. Si ordenáramos a
los sujetos de menor a mayor puntuación directa tendríamos el siguiente orden:
a) Juan, Pedro, Mariana
b) Pedro, Mariana, Juan
c) Pedro, Juan, Mariana
Soluciones:
1. C
2. C
3. B
4. C
5. B
6. A
7. C
8. A
9. B
10. C
11. A