11º) Obtenga el equivalente Thévenin en los terminales AB del

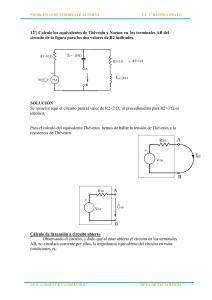
PROBLEMAS DE CORRIENTE ALTERNA
T.I. 1º BACHILLERATO
11º) Obtenga el equivalente Thévenin en los terminales AB del circuito de la figura
I
I2
R2=10
X
A
A
+
R1=5
R3=5
I = 5 30º
XL1= j5
XL2= j5
B
Y
SOLUCIÓN
Para el cálculo del equivalente Thévenin hemos de hallar la tensión de Thévenin y la
resistencia de Thévenin.
A
+
RTH
VTH
UAB
B
+
Como se explico en teoría, la tensión de Thévenin es la tensión que mediríamos, a
circuito abierto, en los terminales del circuito en los que queremos calcular el
equivalente (UAB). Por otro lado, podemos calcular la
resistencia Thévenin RTH como la resistencia vista desde los
A
RTH
terminales AB, dado que no existen fuentes de excitación
dependientes, para lo cual, hay que anular la fuente de
corriente de la figura (recuerde que una fuente de corriente
se anula dejándola en circuito abierto), Finalmente, también
VTH
podemos calcular la corriente de cortocircuito entre los
terminales de AB y utilizarla para el cálculo de UAB y RTH
de no haberlas calculado por otro método.
Icc
B
Cálculo de la tensión a circuito abierto
Calculamos primero la impedancia equivalente del circuito:
Z R1, Xl 1  R1  X L1  5  j 5 
Z R 2 , R 3 , Xl 2  R2  R3  X L 2  10  5  j 5  15  j 5 
Z eq 

Z
R 1, Xl 1
*Z
R 2 , R 3 , Xl 2

Z R1, Xl 1  Z R 2 , R 3 , Xl 2
1000  j 500  j 2000  1000
20 2  10 2
I.E.S. ANDRÉS DE VANDELVIRA

(5  j 5) * (15  j 5)
(5  j 5)  (15  j 5)
2000  j1500
500

50  j100
20  j10

(50  j100) * ( 20  j10)
( 20  j10) * ( 20  j10)
 4  j 3  5 36.87º 
DPTO DE TECNOLOGÍA

PROBLEMAS DE CORRIENTE ALTERNA
T.I. 1º BACHILLERATO
El circuito simplificado queda de la siguiente forma:
X
+
I
I = 5 30º
UXY
Zeq= 4+j3
Y
Debe apreciarse que la tensión en los terminales de la impedancia equivalente no es
UAB.
U XY  Z eq * I  5 36,87º
I2 
U XY
Z R 2 , R 3, Xl 2

* 5 30º  25 66,87º V
25 66,87º

15  j 5
25 66,87º
15,8114 18,435º
 1,58114 48,435º A
U AB  Z R 3 , Xl 2 * I 2  (5  j 5) * 1,58114 48,435º  5 * 2 45º * 1,58114 48,435º  11,18 93,435º V
Cálculo de la impedancia de
Thévenin
Dado que no exiten fuentes de
excitación
independientes,
la
impedancia equivalente del circuito es
aquella que se ve desde los terminales
en los que se quiere calcular el
equivalente Thevenin, anuladas las
fuentes de excitación. En definitiva, es
la impedancia del circuito vista desde
los terminales AB en el circuito. De la
figura.
R2=10
X
R1=5
A
R3=5
XL1= j5
XL2= j5
B
Y
Casualmente, en este caso,
coincide con la impedancia equivalente previamente calculada, habida cuenta que por
un lado tenemos una rama donde R3 está en serie con XL2, y otra, en paralelo con la
anterior, compuesta por R2,R1 y XL1 conectados en serie; de este modo, la impedancia
vista desde los terminales AB es:
Z eq 

Z
R1, Xl 1
*Z
R 2 , R 3 , Xl 2
Z R1, Xl 1  Z R 2 , R 3 , Xl 2
1000  j 500  j 2000  1000
20 2  10 2


( 5  j 5) * (15  j 5)
(5  j 5)  (15  j 5)
2000  j1500
500

50  j100
20  j10

(50  j100) * ( 20  j10)
( 20  j10) * ( 20  j10)

 4  j 3  5 36.87º 
Con los datos calculados concluimos que el equivalente
Thévenin del circuito para los terminales AB es:
RTH=4+j3
+
A
VTH=11,18
93,435º
B
I.E.S. ANDRÉS DE VANDELVIRA
DPTO DE TECNOLOGÍA
PROBLEMAS DE CORRIENTE ALTERNA
T.I. 1º BACHILLERATO
Seguidamente, y únicamente a efectos de comprobación, se calcula la Icc que resulta de
cortocircuitar los terminales.
I
R2=10
X
A
+
A
R1=5
R3=5
I = 5 30º
ICC
XL1= j5
XL2= j5
B
Mediante el concepto de divisor de corriente
I CC 
Z R1, xl 1, R 2
R2
(5  j 5) * 10
50  j 50
4,472 26,5651º
(5  j 5)  10
15  j 5
*I 
* 5 30º 
* 5 30º 
* 5 30º 
10
10
10
 0,4472 26,5651º * 5 30º  2,2361 56,5651º A
Podemos comprobar como se cumple las relación siguiente:
V TH  Z TH * I cc  5 36,87º * 2,2361 56,5651º  11,18 93,435º V
I.E.S. ANDRÉS DE VANDELVIRA
DPTO DE TECNOLOGÍA