2.2 Número reales El conjunto de los números reales está formado

2.2 Número reales
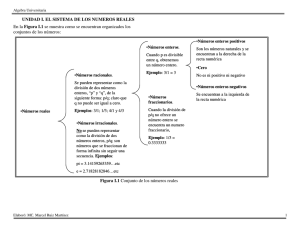
El conjunto de los números reales está formado por una serie de subconjuntos de
números que definiremos a continuación:
Los números naturales que surgen con la necesidad de contar
N = {1, 2, 3, 4,...}
Los números enteros que complementan a los naturales pues son contienen a los
negativos y el cero
Z = {...-3, -2, -1, 0, 1, 2, 3...}
Los números racionales (fraccionarios o quebrados) que son todos aquellos números que
pueden ser representados como el cociente de dos números enteros
Q = {-⅓, -⅖,...⅙ ⅜...}
Y los números irracionales, que son todos aquellos números que no pueden ser
representados como el cociente de dos números enteros. Ejemplos de estos son el
número e, √2 y el número π. Este conjunto se representa con I.
Puesto que los naturales están incluidos en los enteros y todos los enteros pueden ser
representados como un número racional, se dice que los números reales son la unión de
los números racionales y los irracionales.
R = QUI
Gráficamente los números reales son representados con la recta numérica, a cada punto
de una recta se le puede asociar un número real. Además, se dice que se trata de un
conjunto infinito, denso y no numerable, pues de un número real no puede decirse cuál es
el número real anterior y posterior a él.
Todas las operaciones algebraicas que hemos aprendido en nuestros estudios previos: la
suma, la resta, la multiplicación y la división son válidas en el conjunto de los números
reales gracias a las propiedades de estos. De igual forma, todas las operaciones que
estudiaremos en adelante como la derivad y la integral también tendrán validez en este
conjunto.