Método del disparo - Universitat Politècnica de Catalunya

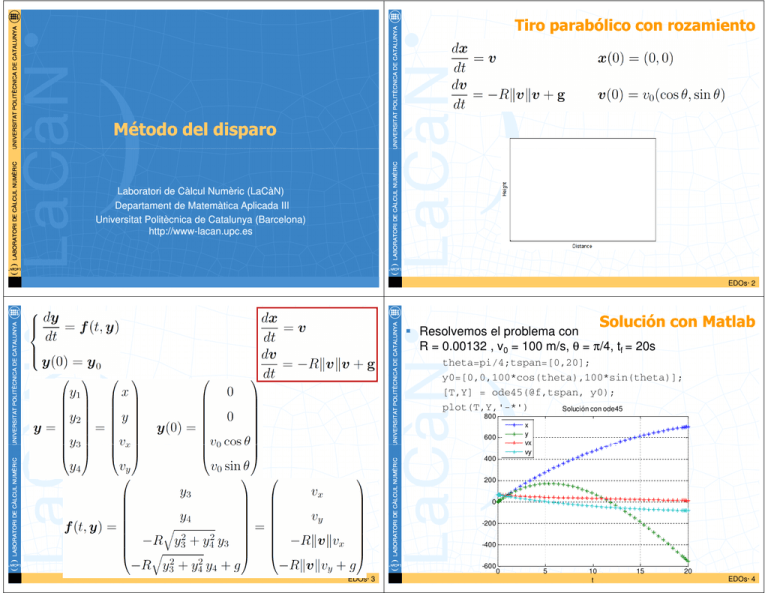
Tiro parabólico con rozamiento
Método del disparo
Laboratori de Càlcul Numèric (LaCàN)
Departament de Matemàtica Aplicada III
Universitat Politècnica de Catalunya (Barcelona)
http://www-lacan.upc.es
EDOs· 2
Solución con Matlab
Resolvemos el problema con
R = 0.00132 , v0 = 100 m/s, θ = π/4, tf = 20s
theta=pi/4;tspan=[0,20];
y0=[0,0,100*cos(theta),100*sin(theta)];
[T,Y] = ode45(@f,tspan, y0);
plot(T,Y,'-*')
Solución con ode45
800
x
y
vx
vy
600
400
200
0
-200
-400
-600
EDOs· 3
0
5
10
t
15
20
EDOs· 4
options = odeset('Events',@criterio_parada);
[t2,Y2]=ode45(@f, tspan,y0, options);
figure(2); hold on; plot(Y2(:,1), Y2(:,2),'r')
Trayectoria
plot(Y(:,1), Y(:,2),'-*')
hold on
plot(500,0,'k+','LineWidth',2,'MarkerSize',12)
function [value,isterminal,direction]=criterio_parada(t,y)
value = y(2);
% detecta cuando este valor es 0
isterminal = 1;
% la integración se detiene cuando value=0
direction = -1; % detecta el 0 sólo si la función decrece
Trayectoria
200
100
Trayectoria
200
0
100
y
-100
0
-200
-100
y
-300
-400
-300
-500
-600
-200
-400
0
100
200
300
400
x
500
600
700
800
-500
-600
EDOs· 5
0
100
200
300
400
500
600
700
800
EDOs· 6
Método del disparo
theta_sol = fzero(@distancia, pi/4);
tspan = [0,20];
y0 = [0,0,100*cos(theta_sol),100*sin(theta_sol)];
options = odeset('Events',@criterio_parada);
[t_sol,Y_sol]=ode45(@f,tspan,y0,options);
Resolvemos para diferentes ángulos de lanzamiento
Trayectoria
300
θ =45.0º
θ =67.5º
θ =56.3º
250
Trayectoria
250
200
200
y
150
150
y
100
50
0
-50
100
50
0
100
200
300
x
400
500
0
600
-50
EDOs· 7
0
100
200
300
x
400
500
600
EDOs· 8
PROBLEMAS DE CONTORNO:
MÉTODO DEL DISPARO
Por ejemplo, se puede imponer en x=b la condición
El problema de contorno (PC) se escribe como
• EDO de orden n
• na condiciones de contorno en x=a
Hasta ahora hemos visto métodos para resolver problemas
de valor inicial.
• nb condiciones de contorno en x=b
IDEA del método del disparo: se plantea el problema de
contorno como un problema de valor inicial.
La generalización del método del disparo para otras
condiciones de contorno no añade dificultad alguna.
EDOs· 9
Se sustituyen las nb condiciones de contorno por condiciones
iniciales ficticias en x=a, planteando el problema de valor
inicial
EDOs· 10
Transformando la EDO de orden n en un sistema de n
EDOs de orden 1, el PVI se escribe como
con vector de incógnitas
y condiciones iniciales
• conocidas/datos del PC
• no conocidas/a determinar
Los nb parámetros βi NO son datos del problema
Evidentemente, la solución y(x) del PVI depende de β
EDOs· 11
EDOs· 12
El método del disparo consiste en determinar las
condiciones iniciales β para que se verifiquen las
condiciones de contorno:
• Para un valor dado de β la resolución numérica con
m pasos del PVI proporciona una aproximación de la
solución
. Se define la función de β
Implementación del método del disparo
1. Definición de una función F que dado β calcule la solución
numérica
y evalúe la verificación de las
condiciones de contorno en x=b
β
resolución
numérica del PVI
• Buscamos β que cumpla
verificación
de las CC
¿verificación CC?
2. Implementación de un método para resolver sistemas no
lineales de ecuaciones, que no necesite el valor analítico de
las derivadas de F (difíciles/imposibles de calcular). Se
utiliza para resolver
β*
sistema no
lineal con nb
ecuaciones y
nb incógnitas
3. Se resuelve el PVI con β* (la solución cumple las CC)
EDOs· 13
EDOs· 14
Resolución del sistema no lineal
Ménsula con grandes flechas
Si β es escalar (una sola condición de contorno en x=b)
se trata de un problema de ceros de funciones
• método de la bisección,
• método de la secante …
Si se trata de un sistema no lineal
• Newton-Raphson aproximando las derivadas,
• métodos quasi-Newton …
EDOs· 15
EDOs· 16
Forma adimensional
Definimos:
EDO de segundo orden:
Condiciones de contorno:
Deformada:
EDOs· 17
EDOs· 18
Ejemplo
L = 2.5; a = 0.5; b = 0.03;
E = 5e10; rho = 3.0e3;
I = a*b^3/12;
V = a*b*L;
m = V*rho;
g = 10;
w = m/L*g;
P = 150*g;
alpha1 = L^3*w/(E*I);
alpha2 = L^2*P/(E*I);
EDOs· 19
EDOs· 20
Resolución con Matlab
α1 = 0.125, α2 = 0.17
Solución para diferentes valores de β
Geometría deformada
0.2
β =0.0
β =0.1
β =0.2
0.15
y
0.1
0.05
0
-0.05
0
0.2
0.4
0.6
x
0.8
1
EDOs· 21