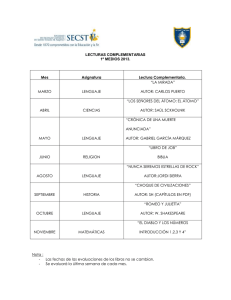
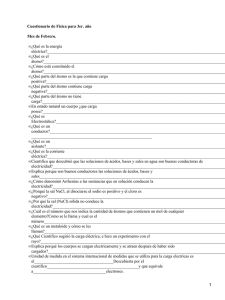
ω ε α ω γ µ λ γ α ε0 ω . λ (m)

Fundamentos de Espectroscopia
r
r
I Considere un átomo bajo un campo eléctrico E = E (t )u z que adquiere un momento dipolar
r
r
p = p(t )u z , en donde p y E están relacionados a través de la ecuación diferencial siguiente;
2
2
&p& + 2γp& + ω 0 p = α 0ε 0ω 0 E (t ) .
1) Explique el significado de esta expresión.
Átomo libre, E(t)=0.
2) Considere un átomo de sodio. Calcular la frecuencia de resonancia ω 0 correspondiente a la
línea de emisión de longitud de onda λ0 = 0.589µm . Sabiendo que γ = 3 x10 7 s −1 , precisar si el
amortiguamiento puede ser considerado débil o importante.
3) Dado el resultado en (2) obtenga la forma general de p(t) de tal suerte que p(0)=p0.
Átomo bajo un campo oscilante E (t ) = E 0 e iωt
r
r
4) Considere la polarizabilidad (compleja) del átomo tal que p = ε 0αE . Obtenga una expresión
para α en función de ω .
5) Trace separadamente la parte real ( Re(α ) ) y la parte imaginaria ( Im(α ) ) de α en función de
ω . Que sucede cuando la frecuencia del campo eléctrico coincide con la frecuencia de
resonancia ω 0 . Que sucede cuando la frecuencia del campo eléctrico es mucho mayor a la de
resonancia ω 0 . Que sucede cuando la frecuencia del campo eléctrico es mucho menor a la de
resonancia ω 0 .
Ne 2
, con N el número de electrones
2m e ε 0 (ω02 − ω2 )
por unidad de volumen. Sabiendo que para H2 a la temperatura de 300K y la presión de 1bar;
II El índice de refracción está dado por; n = 1 +
λ (m)
n
1 + 1.4x10-4
1 + 1.547x10-4
-7
5.46x10
2.54x10-7
a) Calcular N y ω0
b) Comparar N calculada en (a) con el valor que obtendrá usando la ecuación de estado.
c) Mostrar que para interacciones con rayos X ( ≈ 10 5 eV ) el índice de refracción es
esencialmente igual a uno. ¿Le sorprende esto?
d) ¿Por qué n es real? ¿Qué significa esto?
-1-