Distribución de intensidad en un plano posterior de una lente de

Revista
Mexicana
de Físíca 41, No. 5 (1995) 777-782
Distribución de intensidad en un plano posterior
de una lente de Fresnel holográfica en la aproximación
de Fraunhofer
LEO:"EL
TI EYF.S
y AUHELlO
A.
OLIVA
Centro de Desarrollo de Eqnipos e Instrnmentos Científicos (CEDEIC)
Academia de Ciencias de Cuba
Lnz No. 375 el Picota y Compo.,te/a, Habana 10100, Cnba
Hecihido el 5 de agosto de 1994; aceptado el 20 de febrero de 1995
En el presente trabajo ~e obtiene lIna expresión general, utilizando la teoría escalar
ele la difracción, que permite estimar la distribución de intensidades en cualquier plano posterior.
dentro de la aproxima.ción de Frauuhofer. de \lila. lClltc de Fresncl hologréÍ.fica.
RESU~tE~.
ABSTHACT. A general expressioll. within the Fra,unhofer's approximation. which allows to estimatc
th(' intf'llsity distribntion in any plauc, behind a Fresnel holographic lens. is obtained hy applying
thc methods
of the scalar diffraction
theory.
PACS: 42.80.-f; 42.40,-i; 42.10,-5
1. INTHODUCCIÓ"l
3
En los ültimos aiios se ha manifestado un renovado interés en las lentes de Fresnel [1especialtnentc eH las que poseen una alta concentración de zonas [4-10], debido a que
presentan un conjunto int('r('sante de propieda,ks.
Eu geueral. eu estos trahajos se ha
est.udiado el comport.amieuto del freute de onda." en el foco principal. o cuando más. en
los focos secundarios, por ~('r éstos los punt.os de mayor interés.
Por otro lado y ateudielldo a la marcada aherración cromática o dist.ribución del espectro ele la radiación incid('nte a lo largo del eje óptico de una lente de Fresnel holográfica. se
ha realizado una serie de trabajos relacionados con las aplicaciones a la convrrsión dirrcta
d,' energía solar en electricidad. ntiliz;in,lolas como concentradores s('lectivos [11-13]. Para
('st.e fin. el tamaüo finito de la..,;;
celdas fotoc1éct.ricas hace que result(' import.ante conocer no
s6lo el ('omportamiento
('n los focos (principal o secundarios). sino t.ambién ('n geueral. f'U
un ('ntorno de los luismos. lo cual. hasta (,llllOllH'nto. no ha sido ('stlldiado ('011 detalle. Esta.
importaucia está ,lada por varios factores. entre los cuales pndi,'ra citarse. por ejemplo.
la dist.ribución espacial de illtellSi(la(1 para diferentes longit.1Hirs de onda o illtrr\'alos de
longitudes de ouda d(' int('rt's ,I!' acn('rdo con la rt'spnesta es¡",ctral ,ll'l material ele las
fot.ocrldas; el dis('iío d(' la rejilla colectora d(' la c('Ida para optimizar la ('ficirllcia d(~
1,
1
1
convrfsión de la misma. y ot.ros.
En ('stc trahajo S(' oiJtielH'. a partir de la aplic(lcióll de la t.eoría e:"'icalarde la difracción,
HIla expresión que I)('rlllit(~ calcHlar. dl'lltro <1('la aproximaci61l dr Frallllhofer. la distribuC'Íón de illt.pnsida(les t'll un plano posterior cualquiera d(' Hila lellte d(' Frpsllel.
778
LEONEL REYES
Y AURELlO A. OLIVA
y
x
x,
z
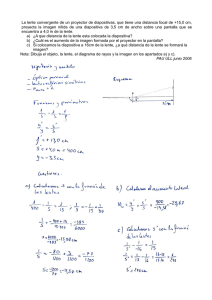
FIGURA
l.
Lente circular
de Frcsnel; a: radio de la primera zona, r¡: radio vector en el plano
z del plano de obsf'rvación (I, y).
(Xl. Yl), ubicado a una distancia
2. DESAIlROLLO
Sean (XI, YI)
situada una
coordenadas,
zona y el al
Se desea
Y (.T, y) dos planos paralelos entre sí, en el primero de los cuales se encuentra
lente circular de Fresnel, de modo tal que su centro coincide con el origen de
tal como IIluestra la Fig. 1. en la que a corresponde al radio de la primera
radio vector en el plano (XI, y¡). El plano (.T, y) será el de observación.
COIlocer
posterior a la placa
cumpla
la función
zOllal
COIl la aproximación
de distribución
de la intellsidad
o lente de Frcsncl, situado a
de Frauuhofer.
tilla
luminosa
La Fig. 2 Illt1('st.ra la fllnción de transmitancia
de una lente de Fresnel, que dada la simetría circnlar del problema,
t(rf)
=
De acuerdo con Gómez-Reino
pf('scntada como
{
1,
'2
2
SI ~2n ~ TI
O,
, 2
SI ~2n+1
:5
tiene la forma
2
< ~2,,+¡'
2
TI
2
< ~2n+2'
y Llopis [141, esta función de transmitancia
1(1';) = ~ +
2
2:
en un plano
distancia z de ~ste tal que
2
-----sen
(2n+1)rr
00
[(2/1
+
l)rr
----TI
,,2
2]
puede ser re-
(1 )
11:::0
Si sr ilumina con una onda plana monocromática
de amplitud .4. que incide de izquierda
a derecha normalmente sobre el plano (XI, YI), la distribución c!e amplitudes inmediatamente despll~s de la lent(' t(,lldrá
la forma
U(XI,Y¡)
= At(I';),
(2)
TeIli('II(io en ('ueuta la f'xpresión para la propagaci6n ele la IH'rtnrhacióll en la aproximaci6n de Frauuhofer dp la teoría escalar de la difracei6n [15], la di:-;tribnción '1))(1') en ('1
DISTHIIlUC¡Ól'
DE I:'<TENSIDAD
El'
U:'< PLA:'<O
POSTERIOR.
. .
779
t
-
2
~2
?
5,=2a J3=3a
FIGUHA 2.
Función
¡:2
;.=4a
2
~2
I
de una lente de Frcsncl.
de trallslllitancia
plano (x, y) a distancia
2
z ,1<,1plano (1:1, yJl, vendrá dada por
(3)
-00
Eu el presente caso, sustituyendo
(2) en (3), se obtiene
eikz . le '1
'
~)(r) = A-. -0'27' F{t(rf)
,AZ
doude F{t(,.¡)}
npsulta
es la transformada
cómodo
utilizar
de Four;er de la fnnción de transmitancia
la siguiente
rikz
¡,
,le
2
..1':"'027'
(1).
notación:
_
= A(r. z)
(211
+
1 = -'").
1/\::
obt (,IlÍf:'ndose
~}(r) =
II(r'Z)F{
~ +)~ i~"s<'n
¡¡aripudo uso de la fórmula d" Euler y d" prop;"dades
s(' oht
[:;"f]}
de la transformada
d,' Fomier
[161.
¡('Ile
¡jJ(p) = A(r.z)
[
.
~'\(p)
L
00
+
.\
::::]
a2
""'1
¡\'" (,'-''''''"
'1
+ e''''''p)
- "" '1 '1
]
.
(4)
780
LEONEL
REYES Y AUHELIO
A.
OLIVA
JI;
donde p =
+ J~, siendo Jx = :"f),z y Jy = yf),z 135 frecuenci35 espaciales en el plano
(x, y) y 6(1') la función delta de Dirac. El primer término de la expresión entre corchetes
representa la onda no difractada por la lente de Fresnel, y eada uno de los otros dos
términos constituye la superposici6n de ondas esféricas. convergentes o divergentes, cuyos
focos se encuentran situados a ambos lados de la placa.
Por otro lado, la ecuación que describe a una lente delgada [171 es como sigue:
. o
,
t(1') = const e'r¡r
Comparando esta expresión con (4), se puede demostrar que cada una de 135 ondas contenid35 en esta última tiene distaucias focales o puntos de convergencia en
JN=,?fN.
Ademá.s, se tiene que para la
1n-(~sill1a zona,
2
(1m
=
se clImple que
2
1na ,
por lo que
2
J N.m
am
= -\'.711"" "
.1.
Como am = R es el radio de la leute con m zon35, y considerando
o foco principal
el foco de primer orden
(N = 1)
que no es más que el resultado conocido de la acentuada aberración cromática o distribución espectral a lo largo del eje óptico, o "resolución axial" de las lentes de Fresnel con
alto número de zonas.
3.
AN,\LISIS
DE LA INTENSIDAD
La intensidad
lo de la onda incidente viene dada por
Restituyendo
en la expresión
(4) los valores de
. .,' {A-;6(1') + LOO
Ji!(1') = e""e''''
21
8=1
(
.4
. Aa
1 J.y2j[A.:;
y p, se obtiene
2
)
[i o.' " + i o.' r']}
e
N(',)'
r
N(',)'
,
(5)
DISTRIIlUCIÓ,
DE I:-iTENSIDAD E:< UI' PLA:<O POSTERIOR.
781
..
que brinda la distribudón
del campo en el plano (x, y) a la distancia z de la placa zona!.
El primer término, que corresponde a la intensidad no difractada, tendrá un valor
(..1./2)2 =
[0/4.
La intensidad que corresponde a cada componente
plano z, depende de los coeficientes de cada término:
En particular,
tiene'
(
4.
de la placa zona!. en el
para los puntos focales, en los cuales se cumple que z
A
que coincide
emergente
con pI resultado,
IV 7f
)2
=
fN
= ,,2 /N
A, se
[o
[(2n
+ 1),,-] 2 '
inferido sin ({('mostrar,
por Gómcz-neino
y Llopis
[14]
CO:<CLUSIO:<ES
Se obtuvo la expresión (5) que brinda la distribución del campo en el plano (x,y) a una
distancia z de la placa zona!. dentro de la aproximación de Fraunhofer, en la que se observa
la d('prndencia explícita de la distribución
de intensidades
con IV, a y A,
V na adecuada simulación Illunérica de esta expresión, con ayuda de computadoras.
permitiría realizar un análisis detallado del comportamiento
de una lente oc Fresnel
caracterizada
por el radio de la primera zona (a), por sus dimensiones (N), y además
teniendo en cuenta la longitud de onoa incidente (A). Obviamente, en el caso de que
incida Ulla luz policrOlwitica.
la distribución
en un plano cualquiera se puede obtener
mediante la superposición
de un conjunto de ondas monocromáticas.
Con la expresión obt.enida. se cuenta COIl una herramienta para pI análisis de la distribución de campo (' int<'llsidades en UIl plano cualquiera posterior de una lente de Fresnel,
correspondiellte
tant.o a los focos principal y secundarios,
como en 1111 ent.orno de ellos.
HEFEHEJ"CIAS
1.
2.
3.
4.
5
6.
'.
8.
L..J. JaHii'ijeYié. J. Oplics 13 (1982) 199.
~1..J. SilllJlson)' A.G. ~lichetle, Opl.ica Acta 31 (1984) 403.
!l. Tanigawa et al.. Oplica Acta 27 (1980) 1327.
!l. Hosokawa)' T. Yalllashila, Appl. Opto 29 (1990) 5106.
!l. ~liHg et al .. Appl. 01'1. 29 (1990) 5111.
~1. Harnna e\ al .. Appl. OJlt. 29 (1990) 5120.
K. ¡';odate et al., ANd. OJlI. 29 (1990) 5115.
Y. Ono)' :\. :\ishida .. ApJlI. 01". 21 (1982) 45.12.
782
9.
lO.
11.
12.
13.
14.
15.
16.
17.
LEONEL REYES Y AURELlO A. OLIVA
R.R.A. Syms y L. Solymar. J.O.S.A. 72 (1982) 179.
L. Reyes y A. Oliva. 1II Simposio de la Sociedad CubaRa de Física. Santiago de Cuba (1985).
N. Aebischer et al., S.P.I.E. 353 (1983) 61.
A. Oliva et al., I Confereneia Internacional de Oplica Aplieada a la Energía Solar, Checoslovaquia (1984).
Y.\V. Zhang et al., Appl. Opto 27 (1988) 3556.
C. Gómez-Reino y J. Llopis. Opl. Pura y Aplic. 10 (1977) 75.
J.\V. Goodman, Introduction to Fourier Oplies, McGraw-HilI, New York (1968).
R.N. Bracewell, The Fourier Transform and ils Applications. :VlcGraw-HilI, New York (1965).
M. Boro y E. \Voll. Principies of Optics, Pergamon Press, New York (1975).