Prob Tema 1_ Resueltos (II)

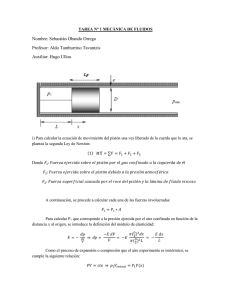
Facultad de Ciencias
Grado de Óptica y Optometría
Curso 2010-2011
Física
SOLUCIONES PROBLEMAS FÍSICA.
TEMA 1: MECÁNICA DE SÓLIDOS Y FLUIDOS
1. Una gota esférica de mercurio de radio 3,0 mm se divide en dos gotas iguales. Calcula a)
el radio de las gotas resultantes y b) el trabajo que hay que realizar contra las fuerzas de
tensión superficial para realizar esta operación. La tensión superficial del mercurio es 0,47
J/m2.
a) El volumen de la gota inicial de mercurio se divide en dos. Supuestas las gotas esféricas:
4
4
1
1
π R3 = 2· π r 3 
→ r = 3 R = 3 3, 0 = 2, 4 mm
3
3
2
2
b) El trabajo necesario será proporcional a la variación de superficie:
W = σ∆S = σ ( 2·4π r 2 − 4π R 2 ) = 4πσ
(
3
)
2 − 1 R 2 = 14 µ J
2. Se introduce un capilar de vidrio de 1,0 mm de diámetro hasta el fondo de un vaso de
agua de 15 cm de profundidad y se sopla hasta formar burbujas de aire. a) Determina el
exceso de presión del aire respecto a la presión atmosférica en el interior de las burbujas,
suponiendo que éstas tienen el mismo diámetro que el capilar. b) Calcula lo que asciende
o desciende el agua por el capilar respecto a la superficie del agua cuando se deja de
soplar. Supón que el ángulo de contacto del agua con la superficie de vidrio es
aproximadamente 0º. c) Si se sustituye el agua por glicerina, ¿habrá que soplar con mayor
o menor fuerza para formar las burbujas? d) ¿es mayor o menor el nivel de la glicerina
respecto al agua en el capilar cuando se deja de soplar? Supón que el ángulo de contacto
de la glicerina con la superficie de vidrio también es aproximadamente 0º. Datos:
σagua=72,8 mN/m, σglicerina=63,1 mN/m, ρglicerina=1,26·103 kg/m3
a) El exceso de presión en el interior de las burbujas será:
p = patm + ρ gh +
2σ
2σ
2·72,8·10−3

→ p − patm = ρ gh +
= 1000·9,8·0,15 +
= 1760 Pa
R
R
0,5·10−3
b) La altura a la que sube el agua por el capilar es:
2σ cos θ
2·72,8·10−3
h=
=
= 0, 030 m
1000·9,8·0,5·10−3
ρ gR
Facultad de Ciencias
Grado de Óptica y Optometría
Curso 2010-2011
Física
c) Si cambiamos por glicerina, el exceso de presión será:
2σ '
2σ '
2·63,1·10−3
p ' = patm + ρ ' gh +

→ p '− patm = ρ ' gh +
= 1260·9,8·0,15 +
= 2100 Pa
R
R
0,5·10−3
luego habrá que soplar con mayor fuerza.
d) La altura a la que sube la glicerina es:
h' =
2σ 'cos θ
2·63,1·10−3
=
= 0, 020 m
1260·9,8·0,5·10−3
ρ ' gR
3. El venturímetro es un dispositivo empleado para la
medida del caudal de líquido que fluye por una
∆h
tubería y se basa en la medida de la diferencia de
alturas ∆h en dos manómetros de tubo abierto, uno
D1
en la tubería y otro en un estrechamiento practicado
D2
en la tubería. a) Calcula la diferencia entre la presión en la tubería y la presión en el
estrechamiento si ∆h = 10 cm y el líquido que circula es agua. b) Sabiendo que el diámetro
de la tubería es D1= 6,0 cm y el del estrechamiento D2=3,0 cm, calcula la velocidad del
agua en la tubería. c) Calcula el caudal del agua en la tubería en L/s.
a) La diferencia de presión se obtiene a partir de la diferencia de alturas que alcanza el líquido
en los dos manómetros de tubo abierto:
∆p = p1 − p2 = ρ g ∆h = 1000·9,8·0,1 = 980 Pa
b) Aplicamos la ecuación de Bernoulli entre la tubería y el estrechamiento, tomando en dichos
puntos el origen de alturas:
p1 +
1 2
1
1
1
ρ v1 = p2 + ρ v22 
→ ∆p + ρ v12 = ρ v22
2
2
2
2
Además, se cumple la ecuación de continuidad:
D12
D22
D12
36
S1v1 = S 2 v2 
→π
v1 = π
v2 
→ v2 = 2 v1 = v1 = 4v1
4
4
D2
9
Por lo tanto, ∆p +
1 2 1
1
2∆p
2·980
m
ρ v1 = ρ16v12 
→ ∆p = 15 ρ v12 
→ v1 =
=
= 0,36
2
2
2
15 ρ
15·1000
s
c) El caudal en la tubería es: I v = π
D12
m3
L
v1 = 1, 0·10 −3
= 1, 0
4
s
s
Facultad de Ciencias
Grado de Óptica y Optometría
Curso 2010-2011
Física
4. Un depósito de agua muy grande se vacía a través de una tubería como se indica en la
figura. Sabiendo que h=2,0 m, h1=0,8 m,
S1=2,0 dm2 y S2=1,0 dm2, determina a) la
velocidad de salida en las secciones S1 y S2;
a
h
b) la presión en la sección S1; c) la altura que
alcanzará el agua en el tubo conectado a
h1
dicha tubería.
S1
S2
a) Aplicando la ecuación de Bernoulli entre la parte superior del depósito y S2:
1
2
ρ gh + patm = ρ v22 + patm 
→ v2 = 2 gh = 2·9 ,8·2 = 6 , 26
m
s
Aplicando la ecuación de continuidad entre 1 y 2:
S1v1 = S 2 v2 
→ v1 =
S2
m
v2 = 3,13
S1
s
b) Aplicando la ecuación de Bernoulli entre la parte superior del depósito y S1:
1

1

ρ gh + patm = ρ v12 + ρ gh1 + p1 
→ p1 = patm + ρ  g ( h − h1 ) − v12 
2
2 

1


p1 = 101.000 + 1000 9 ,81
· , 2 − 3,132  = 108.000 Pa
2


c) A partir de la expresión de la presión en el interior del fluido podemos obtener la altura pedida:
p1 = patm + ρ ga 
→a =
p1 − patm
= 0,7m
ρg
5. Una piscina de 10 m x 5,0 m y 2,0 m de profundidad, está llena de agua hasta 10 cm del
borde. Durante una fuerte tormenta, el agua alcanzó el borde en una hora. a) ¿Cuántos
L/m2 cayeron en esa hora? En el fondo de la piscina se encuentra la llave de paso del
desagüe, de radio 10 cm y conectada a la cañería general donde la presión es de 0,11 MPa.
b) Calcula la velocidad a la que sale el agua de la piscina cuando se abre totalmente la
llave de paso. c) ¿Cuánto tiempo hay que dejar la llave abierta si se quiere vaciar la
piscina para dejarla como estaba inicialmente? d) ¿En qué porcentaje debería reducirse la
sección de la llave de paso para que este vaciado se realizara en una hora?
Facultad de Ciencias
Grado de Óptica y Optometría
Curso 2010-2011
Física
a) Inicialmente había en la piscina un volumen de agua es: VI = 10 × 5 × 1,9 = 95 m3 . En una
hora, el volumen de agua en la piscina es: VF = 10 × 5 × 2 = 100 m3 . Por lo tanto han caído 5000
L de agua sobre una superficie de 50 m2. Conclusión la cantidad de lluvia caída en una hora
es de 100 L/m2.
b) Aplicando la ecuación de Bernoulli entre la parte alta de la piscina y el desagüe, se tiene:
patm + ρ gh = p +
=
2 ( patm + ρ gh − p )
1 2
→v =
=
ρ v 
2
ρ
2 (1, 01·105 + 1000·9,8·2 − 1,1·105 )
1000
= 4, 6
m
s
c) A partir de la definición de caudal se tiene:
I v = S·v =
V
V −V
5

→t = F 2 I =
= 35 s
t
π ·R ·v π ·0, 01·4, 6
d) Si se desea que t’ = 3600 s, entonces:
S '·v =
V
V − VI S·t

→S ' = F
=
= 0, 0097·S
t'
v·t '
t'
Hay que reducir la sección en un 99 %.
6. Un tubo de Pitot es un dispositivo usado para medir la
velocidad de gases en tuberías. Consideraremos el gas de
densidad constante ρ = 1,83 kg / m3 y que el líquido del tubo
manométrico tiene una densidad ρ L = 1000 kg / m3 . Teniendo
en cuenta que la conducción del gas es de izquierda a derecha
y que la velocidad de éste en el punto 2 es nula, a) determina
la velocidad del gas en el punto 1 sabiendo que h = 1, 5 cm . b) Conociendo que la tubería
tiene un diámetro de 1 cm, determina el caudal en L/s. c) Si cada metro cúbico de gas
cuesta 0,5 € ¿cuánto cuesta mantener dicho caudal durante una hora?
a) Aplicamos la ecuación de Bernoulli entre los puntos 1 y 2:
p2 =
1 2
1
ρ v1 + p1 
→ p2 − p1 = ρ v12
2
2
Aplicamos la ecuación fundamental de la hidrostática en el tubo manométrico:
Facultad de Ciencias
Grado de Óptica y Optometría
Curso 2010-2011
Física
p2 = p1 + ρliquido gh 
→ p2 − p1 = ρliquido gh
Igualando las dos expresiones anteriores y despejando se tiene:
v´ 1 = 2
ρliquido gh
1000·9 ,81
· ,510
· −2
m
= 2
= 12, 7
1,83
s
ρ
b) El caudal viene dado por el producto de la sección y la velocidad del fluido:
Q = S·v1 = π
D2
m3
L
·v1 = 10−3
= 1, 00
4
s
s
c) El coste económico vendrá dado por el producto entre el caudal, el tiempo y el coste de
cada metro cúbico:
Coste = Q·t·c = 10−3 ·3600·0 ,5 = 1,8 ∈
7. Por un tubo horizontal con un diámetro interior de 2,6 mm y una longitud de 30 cm
circula aceite con una velocidad de 9,0 cm/s. Calcula a) el flujo de volumen y b) la
diferencia de presiones que se necesita para impulsar el aceite. c) Calcula el porcentaje en
que varía el flujo de volumen cuando el diámetro se reduce un 5%. Viscosidad del aceite
= 0,391 Pa·s.
a) El flujo de volumen viene dado por:
2
I v = S·v = π · R 2 ·v = π ·( 0,13) ·9 = 0, 48
cm3
s
b) Según la ley de Poiseuille:
I v ·8η·l π · R 2 ·v·8η·l v·8η·l 0, 09·8·0, 391·0,3
∆p =
=
=
=
= 50 kPa
2
R2
π ·R 4
π ·R 4
(1, 3·10−3 )
c) El nuevo caudal será:
4
∆pπ R '4 ∆pπ ( 0,95R )
4
Iv ' =
=
= ( 0,95 ) I v = 0,81I v
8η l
8η l
Por lo tanto, el caudal se reduce un 19%.