Inductores y Capacitores
Anuncio
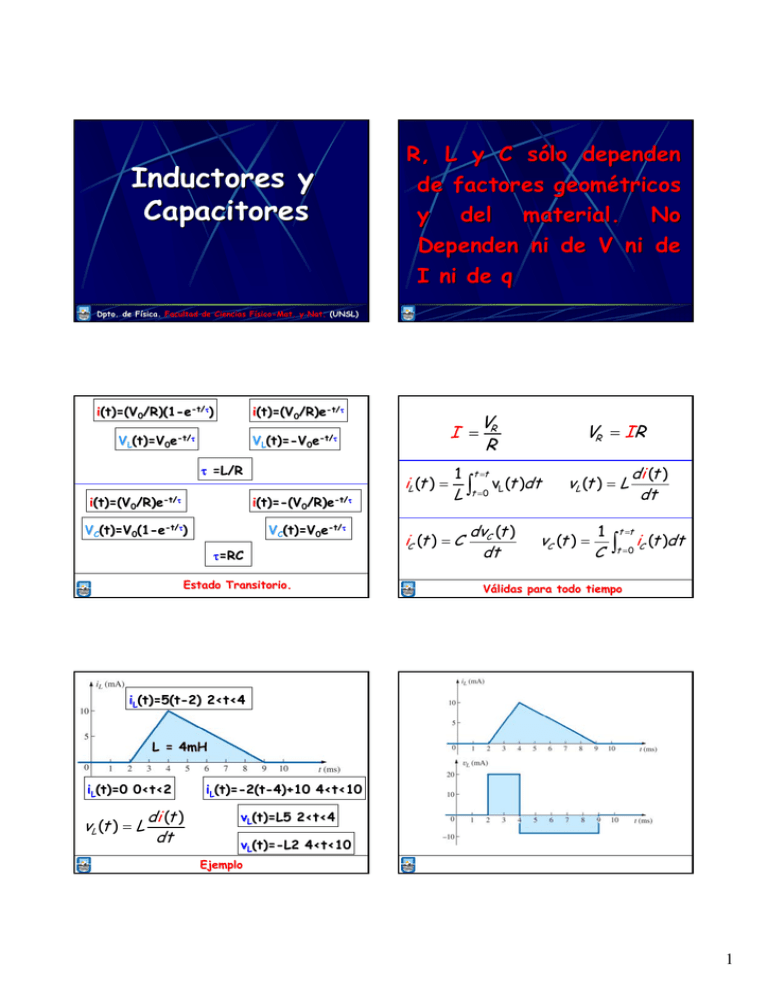
Inductores y Capacitores R, L y C sólo dependen de factores geométricos y del material. No Dependen ni de V ni de I ni de q Dpto. de Fí Física. Facultad de Ciencias Fí Físicosico-Mat. y Nat. (UNSL) t/τ) i(t)=(V (t)=(V0/R)(1/R)(1-e-t/τ t/τ i(t)=(V (t)=(V0/R)e-t/τ t/τ VL(t)=V (t)=V0e-t/τ I = t/τ VL(t)= -V0e-t/τ (t)=- τ =L/R t/τ i(t)= (t)=((V0/R)e-t/τ t/τ i(t)= -(V0/R)e-t/τ (t)=- t/τ) VC(t)=V (t)=V0(1(1-e-t/τ t/τ VC(t)=V (t)=V0e-t/τ τ=RC Estado Transitorio. iL (t ) = 1 t =t L ∫t iC (t ) = C VR R =0 VR = IR νL (t )dt dvC (t ) dt vL (t ) = L vC (t ) = 1 C di (t ) dt t =t ∫t =0 iC (t )dt Válidas para todo tiempo iL(t)=5(t -2) 2<t<4 (t)=5(tL = 4mH iL(t)=0 (t)=0 0<t<2 vL (t ) = L di (t ) dt iL(t)= -2(t(t)=2(t-4)+10 4<t<10 vL(t)=L5 (t)=L5 2<t<4 vL(t)= -L2 4<t<10 (t)=Ejemplo 1 Corriente Alterna (AC) Importancia: Generador de Corriente Alterna Flujo magné magnético: ΦB =BACosθ BACosθ Flujo magné magnético: ΦB =BACosθ BACosθ Ley de Faraday: ε = −N Ley de Faraday: ε = −N ∆ΦB ∆t θ= ωt ∆ΦB ∆t ε(t) =(NABω =(NABω)sen(ω )sen(ωt) εMáx = NABω NABω ε(t) = εMáx sen(ωt) 2 f=? f=1/0.4s = 2.5 Hz f=1/T f=1/0.5s = 2 Hz Frecuencia: Nú Número de ciclos por segundo. Se Mide en [Hz]= 1/s Polaridades: Objetivo: Determinar como “responden” responden” R, L y C a las tensiones (corrientes) alternas v(t)= Vmsen( v(t)=V sen(ωt) Formato general: Tensióón [V] Tensi Vm Frecuencia f = 1/T ω=2π =2πf v1 Tiempo [s] Vpp Vm Perí Período (T) [s] Que pasa con la forma de la respuesta? 3 Fase: cos α =sen (α (α+90º +90º) cos (α (α-90º 90º) = sen α v(t)= Vmsen( v(t)=V sen(ωt±φ) Ejemplo: v(t)=10sen( ωt+30 v(t)=10sen(ω t+30º) v(t)=2sen( ωt+10 v(t)=2sen(ω t+10º) i(t)= -sen(ω i(t)=sen(ωt+30 t+30º) i(t)=5sen( ωt+70 i(t)=5sen(ω t+70º) v ADELANTA a i, 160º 160º i(t)= -sen(ω ωt+30 ωt-150º i(t)=sen(ωt+30 t+30º)=sen( )=sen(ω t+30º-180º 180º)=sen( )=sen(ω 150º) v Adelanta a i, 160º 160º i(t)= -sen(ω ωt+30 sen(ω ωt+210º i(t)=sen(ωt+30 t+30º)=sen( )=sen(ω t+30º+180)= +180)=sen( t+210º) Diferencia de fase= 40º 40º, i ADELANTA a v. Valor Medio: YMedio = 1 T T ∫ y (t )dt 0 v(t)= Vmsen( v(t)=V sen(ωt±φ) i Adelanta a v, 200º 200º Valor Eficaz: YEficaz = 1 T T ∫ y (t ) dt 2 0 v(t)= Vmsen( sen(ωt±φ) v(t)=V Veficaz=Vm/(√ /(√2) = 0.707Vm 4 Valor Eficaz 0.707 Vm Valor Medio: 0.637 Vm Una corriente alterna tiene un valor EFICAZ de I Amperes si, al circular a travé través de la resistencia dada, origina en dicha resistencia una cantidad de calor media, por unidad de tiempo, igual al que producirí produciría una corriente CONTINUA de valor I. Una corriente alterna tiene un valor EFICAZ de I Amperes si, al circular a travé través de la resistencia dada, origina en dicha resistencia una cantidad de calor media, por unidad de tiempo, igual al que producirí produciría una corriente CONTINUA de valor I. vR(t)= Vmsen( (t)=V sen(ωt) Respuesta de R, L y C a la Corriente Alterna. Fasores. Aplicando la Ley de Ohm: I=V/R iR(t)= vR(t)/R=( Vm/R)sen( (t)=v (t)/R=(V R)sen(ωt) iR(t)= Imsen( (t)=I sen(ωt) ; Im=(V =(Vm/R) Corriente y Tensió Tensión está están en FASE en una Resistencia Dpto. de Fí Física. Facultad de Ciencias Fí Físicosico-Mat. y Nat. (UNSL) iL(t)= Imsen( (t)=I sen(ωt) di (t ) vL = L L dt vL(t)=( LImω)cos(ω (t)=(LI )cos(ωt); Vm=Im(ωL) vL(t)= Vmsen( (t)=V sen(ωt+90º +90º) XL=ωL La Tensió Tensión adelanta 90º 90º a la Corriente en un inductor vC(t)= Vmsen( (t)=V sen(ωt) iC = C dvc (t ) dt iC(t)=( CVmω)cos(ω (t)=(CV )cos(ωt); Im=Vm(ωC) iC(t)= Imsen( (t)=I sen(ωt+90º +90º) XC=1/ω =1/ωC La Corriente adelanta 90º 90º a la Tensió ó n Tensi en un capacitor. capacitor. 5 Ejemplo: Dada la corriente a travé través de un inductor de 0.1 H. Determine vL(t). (t). iL(t)= Imsen( (t)=I sen(ωt) vL(t)= Vmsen( (t)=V sen(ωt+90º +90º) iL(t)=10sen(377t) (t)=10sen(377t) Vm=ImXL XL=ωL iL(t)=10sen(377t) (t)=10sen(377t) Im=10A ; ω=377rad/s XL=(377rad/s)(0.1H)=37.7 Ω Vm=(10A)(37.7Ω =(10A)(37.7Ω)=377V vL(t)=377sen(377t +90ºº) (t)=377sen(377t+90 vL(t)=377sen(377t +90ºº) (t)=377sen(377t+90 Notació Notación Fasorial: Fasorial: y(t)= Ymsen( y(t)=Y sen(ωt+φ t+φ) ⇒ Y = YEficaz ∠φ° vR(t)= Vmsen( (t)=V sen(ωt) ⇒ VR = VR ∠0° iR(t)= Imsen( (t)=I sen(ωt) ⇒ I R = IR ∠0° VR Circuito Inductivo: vL(t)= Vmsen( (t)=V sen(ωt) Æ IR VL = V ∠0° Ley de I = VL ∠0° = VL ∠(0° − φ ) L L Ohm: XL ∠φL XL V V I L = L ∠(0° − 90°) = L ∠ − 90° XL XL φL=90º =90º I L = I ∠ − 90° Z L = XL ∠90° VL IL VR = VR ∠0° Ley de Ohm: φR:0Æ :0Æ I = I = V ∠0° V = ∠(0° − φR ) R ∠φR R V ∠0° V V = ∠(0° − 0°) = ∠0° R ∠0° R R ZR = R ∠0° Impedancia Resistiva Circuito Inductivo: VL = V ∠0° VL I L = I ∠ − 90° IL VL = V ∠90° VL I L = I ∠0° Z L = X L ∠90° IL 6 Circuito Capacitivo: vC(t)= VCsen( (t)=V sen(ωt) Æ VC = V ∠0° V ∠0° VC Ley de = ∠(0° − φC ) I = C Ohm: C XC ∠φC XC V V IC = C ∠(0° − ( −90°)) = C ∠90° XC XC φC=-90º 90º IC = I ∠90° ZC = XC ∠ − 90° Ejemplo: Utilizando álgebra compleja determine la corriente del circuito. Grafique. 24 v = 24sin(ωt) ⇒ V = ∠0° = 16.968∠0° 2 V V ∠ 0° 16.968∠0° I = = = = Z L X L ∠90° 3Ω∠90° I = 5.656A∠ − 90° i (t ) = 2(5.656) sin(ωt − 90°) = 8sin(ωt − 90°) IC 16.968V VC Impedancias en Serie: 5.656A Ejemplo: Determine la ZT: I V Triá Triángulo de Impedancias φT ZT = R 2 + XL2 φT = Arctg XL R Ley de Ohm en AC: V I = Z OJO!!! V e I son FASORES!!! 7 V = 50∠0° I = 10∠ − 53.13° VR = 30∠ − 53.13° VL = 70∠36.87° VC = 30∠ − 143.13° Diagrama de Fase Mié Miércoles 23: Laboratorio 3 Diferencia de Fase Circuito Serie RC Repaso 2πrad=360 º rad=360º 8 Proyecció Proyección vertical de un vector rotatorio ω=2π =2πf [rad/s] rad/s] 9