Circunferencia

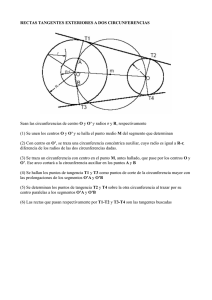
Tema03: Circunferencia
1
3
Circunferencia
3.0 Introducción
La definición de circunferencia es clara para todo el mundo. El uso de la circunferencia
en la práctica y la generación de superficies de revolución, cuyas secciones son
circunferencias, están a la vista, desde tuberías, depósitos cilíndricos, depósitos
esféricos para contener gases licuados, hasta los cascos de algunos buques, en especial
algunos tipos de catamaranes.
Una propiedad geométrica poco conocida de la circunferencia es la de ser el lugar
geométrico con mínimo perímetro para máxima área encerrada. Extrapolando a un
cilindro cerrado, contendría el máximo volumen, con la mínima superficie lateral, y lo
mismo puede decirse de la esfera.
Por esta razón, las perdidas por rozamiento o por transmisión de calor (proporcionales a
la superficie) en tuberías de sección circular son inferiores a las que se obtienen con
tubería de cualquier otro tipo de sección. Constructivamente, las superficies cilíndricas
son sencillas de construir por ser su radio de curvatura constante.
3.1 Definiciones y propiedades
Se define como circunferencia de radio R y centro O al lugar geométrico de los puntos
del plano que equidistan una distancia R de un punto O llamado centro. La longitud de
la circunferencia es L = 2.π .R ; Circulo es la superficie limitada por la circunferencia su
área es A = π .R 2 .
Se define como sector circular la porción de círculo comprendida entre dos semirectas
que pasan por el centro de dicho círculo (Fig.1). El área de este sector circular se calcula
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
2
en función del ángulo que abarcan estas dos semirectas. Si expresamos el ángulo α que
forman estas semirectas en grados:
R
S=
α
360
⋅π ⋅ R 2
Fig. 1 Área del sector circular
Se citan a continuación algunas propiedades de la circunferencia:
♣ Las tangentes a la circunferencia, cumplen que si el punto de tangencia se une con el
centro de la circunferencia, esta recta es perpendicular a la recta tangente.
♣ Se denomina cuerda de una circunferencia al segmento que une los dos puntos de
corte de esta con cualquier recta que la corte. La perpendicular desde el centro de la
circunferencia a esta cuerda la corta en su punto medio (Fig. 2).
♣ Una circunferencia A corta a otra B diametralmente, si uniendo los puntos de corte P
y Q, esta recta pasa por el centro de A. El segmento PQ será un diámetro de la
circunferencia B (Fig. 3).
P
A
O
O
M
B
Cuerda
Fig. 2 Cuerda
Q
Fig. 3 Circunferencias diametrales
3.2 Teorema del ángulo central
Si se trazan dos radios de una circunferencia, y los extremos de estos radios se unen con
un punto cualquiera de la misma (Fig. 4) se cumple que los ángulos formados por las
cuerdas y los radios cumplen 2 · β = γ.
En efecto, de la Fig. 4 se ve que x + y + γ = 360º y que x = 180 – 2 · α, y = 180 – 2 · β
con los que sustituyendo se tiene que α + β = ½ · γ. A esta relación entre ángulos se le
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
3
llama teorema del ángulo central y es la base teórica para el trazado del arco capaz de
un segmento, que se usa entre otras cosas en navegación.
x
y
Fig. 4 Teorema del ángulo central
3.3. Arco capaz de un segmento y un ángulo
El arco capaz de un segmento AB y un ángulo α dados, es el lugar geométrico de los
puntos del plano respecto a los cuales el segmento se ve bajo un ángulo α.
Para trazar el arco capaz del segmento AB, se traza por su extremo A una semirecta con
un ángulo α, y por el extremo A se traza una perpendicular a dicha semirecta. Se traza
además la mediatriz del segmento AB. Donde se corten ambas rectas, es el centro O del
arco capaz del segmento AB (Fig. 5).
α
O
α
A
α
B
Fig. 5 Arco capaz de un segmento
Una propiedad del arco capaz es la siguiente (Fig. 6): tomando un punto cualquiera (P,
P’,...) de un arco capaz de un segmento AB, la bisectriz del ángulo en dicho punto
siempre pasa por el punto M, intersección de la mediatriz de AB con el arco capaz.
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
4
Fig. 6 Propiedades del arco capaz
3.4 Potencia de un punto respecto a una circunferencia
Se define como potencia de un punto P respecto a una circunferencia al producto de las
distancias entre el punto P y los puntos S y Q de corte de una secante cualquiera a la
circunferencia, pasando por el punto P.
Se cumple que este valor es constante para cualquier secante que pase por el punto P
(Fig. 7). Como límite de las rectas secantes, se tiene la tangente a la circunferencia
desde P. El punto de tangencia será un punto doble.
T
S
Q
P
T
U
Pot = PT 2 = PQ.PS = PT .PU
Fig. 7 Potencia
3.5 Eje radical de dos circunferencias
Se define como eje radical de dos circunferencias al lugar geométrico de los puntos del
plano que tienen igual potencia respecto de las dos circunferencias.
♣ Si las circunferencias se cortan (Fig. 8), el eje radical es la recta que pasa por los dos
puntos de corte, al tener ambos puntos potencia nula respecto a las dos circunferencias.
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
5
♣ El eje radical de dos circunferencias es perpendicular a la recta que une los centros de
ambas, consecuencia de lo anterior.
Para trazar en eje radical de dos circunferencias que no se cortan (Fig. 9), se traza una
circunferencia auxiliar que corte a ambas, y se trazan los ejes radicales m y n. Estos se
cortan en un punto P. La perpendicular s a la recta que une los centros de las
circunferencias O1 y O2 por el punto P es el eje radical buscado.
s
m
O1
O2
P
O1
n
O2
Fig. 9 Eje radical
Fig. 8 Eje radical
Algunas propiedades del eje radical:
♠ Como los puntos del eje radical tienen igual potencia respecto a las dos
circunferencias, para cualquier punto P del eje radical s, si desde este punto se trazan las
tangentes a las dos circunferencias, las longitudes de los segmentos tangentes serán las
mismas (Fig. 10). Esto posibilitará la resolución de algunos problemas de tangencias.
♠ Como consecuencia de lo anterior, el eje radical s de dos circunferencias de centros
O1 y O2, será el lugar geométrico de los centros de las circunferencias ortogonales a
dichas circunferencias (Fig. 10).
s
O1
O2
T1
T2
l
l
P
Fig. 10 Propiedades del eje radical
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
6
3.6 Centro radical de tres circunferencias
Se define como centro radical de tres circunferencias el punto C que tiene igual potencia
respecto de las tres circunferencias. Se calcula (Fig. 11) como el punto de corte de dos
de los ejes radicales s y t de las circunferencias tomadas dos a dos.
s
O1
O2
t
C
O3
Fig. 11 Centro radical
Propiedades del centro radical:
♦ Como es la intersección de tres ejes radicales, las longitudes de los seis segmentos
tangentes a las tres circunferencias serán iguales (d).
♦ Será centro de una circunferencia ortogonal (Fig. 12) a las tres y de radio d.
O1
O2
d
d
d
d
C
d
d
O3
Fig. 12 Propiedades del centro radical
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
7
3.7 Polar respecto a un punto y una circunferencia
Se denomina polar respecto a un punto P (polo) y una circunferencia directora de centro
O a la recta s que es el eje radical de la circunferencia de diámetro OP y de la
circunferencia directora.
♣ El punto P puede ser exterior (Fig. 13) o interior a la circunferencia (Fig. 14).
♣ La polar es perpendicular a la recta que une P y el centro O de la circunferencia.
Fig. 13 Polar con P exterior
Fig. 14 Polar con P interior
Cuando P es interior, se levanta la perpendicular a OP por P, y se traza la circunferencia
que pase por los puntos O y los de corte M y N. Cortará a la recta OP en T. La
perpendicular a OP por T es la polar pedida. También puede hacerse como dice la teoría
trazando el eje radical de la circunferencia directora y de la de diámetro OP, o bien
haciendo la tangente al círculo director por M, que cortará a la recta OP en el punto T.
Si el polo P está en la circunferencia directora, la polar es la tangente a la circunferencia
directora en P. Si el polo P coincide con el centro O de la circunferencia directora, la
polar es una recta impropia, es decir está en el infinito.
3.7.1 Triangulo Autopolar
Si se toma un punto cualquiera Q (Fig.
15) de la polar m asociada a un polo P,
la polar n de Q pasa por el punto P,
debido a las propiedades ya vistas del
eje radical.
Fig. 15 Triángulo Autopolar
Apuntes de Geometría plana
Si se extiende la polar n hasta que
corte a la polar m en un punto U (Fig.
16), los puntos Q, P y U formarán un
triángulo autopolar respecto a la
circunferencia directora. La propiedad
de un triángulo autopolar es que un
vértice cualquiera es el polo del lado
opuesto, respecto a la circunferencia
directora.
ETSI Navales
Tema03: Circunferencia
8
Hay infinitos triángulos autopolares respecto a un círculo director. Todos ellos tienen un
ángulo obtuso y un vértice en el interior del circulo director
Fig. 16 Triángulo autopolar
Si dado un círculo director y un punto exterior P (Fig. 17, izquierda), se trazan dos
secantes a dicho circulo se obtienen 4 puntos de cortes A, B, C, D que forman un
cuadrilátero. Si se trazan las diagonales de dicho cuadrilátero, estas se cortan en un
punto U. Pues bien, el triángulo PQU es un triángulo autopolar, como puede verse al
dibujar las polares de P, Q y U trazando las tangentes.
Los puntos A, B, C, D son un cuadrilátero inscriptible y por lo tanto las bisectrices de
los ángulos CPA y CQD serán perpendiculares (Fig. 17, derecha), tal como se vio en el
tema sobre cuadriláteros. Luego, si un cuadrilátero es inscriptible, la intersección de sus
diagonales y de las prolongaciones de sus lados, forman un triángulo autopolar respecto
al circulo director que pase por esos cuatro puntos.
Fig. 17 Trazado de triángulos autopolares
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
9
3.8 Tangente desde un punto exterior a una circunferencia
Para trazar las tangentes desde un punto exterior a una circunferencia de centro O, nos
basaremos en las propiedades del eje radical (Fig. 18).
T1
O
M
P
T2
Fig. 18 Tangente a una circunferencia desde un punto exterior
Si trazamos el arco capaz de 90º del segmento PO (circunferencia de centro M, punto
medio de PO), los puntos de corte T1 y T2 unidos con O y P formarán 90º. Como T1O y
T2O son radios de la circunferencia y T1P y T2P perpendiculares a los mismos, estos
últimos segmentos son por tanto tangentes a la circunferencia.
3.9 Tangentes exteriores a dos circunferencias
Para trazar las rectas tangentes exteriores a dos circunferencias de centros O1 y O2 y
radios R1 y R2, se transforma el problema en un problema de trazar las tangentes desde
un punto exterior a una circunferencia (Fig. 19).
T1
T3
1
T'1
R1
O1
M
R
2
-R
O2
2
T'2
T4
T2
Fig. 19 Tangentes exteriores a dos circunferencias
Para ello se ha de transformar una circunferencia en un punto “restando” a los
elementos del problema el menor radio, en nuestro caso, R1. Así, la circunferencia de
radio R1 se transforma en su centro O1 y la de centro O2 en otra circunferencia del
mismo centro y radio R2 – R1.
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
10
Si se trazan las tangentes desde O1 a la nueva circunferencia se obtienen los puntos de
tangencia T’1 y T’2. Ahora hay que deshacer la transformación que hemos realizado
volviendo a sumar R1 a todos los elementos. Los puntos de tangencia obtenidos se
transforman e T1y T2 y serán los puntos de tangencia en la circunferencia de centro O2.
Para obtener los puntos de tangencia en la circunferencia de centro O1 se trazan
paralelas a T1O2 y T2O2 desde O1 para obtener los puntos de tangencia T3 y T4. Basta
unir los puntos de tangencia T3 con T1 y T4 con T2 para tener las tangentes buscadas.
3.10 Tangentes interiores a dos circunferencias
La transformación a realizar es parecida a la del punto 3.9, basta “restar” en “sentido
contrario”. La circunferencia de centro O1 se transforma en su centro, mientras que la de
centro O2 se transforma en otra de centro O2 y radio R1 + R2 (Fig. 20).
R1
M
O1
R2
T1
T4
+R
1
T'1
O2
2
T3
T2
T'2
Fig. 20 Tangentes interiores a dos circunferencias
Si se trazan las tangentes desde O1 a la nueva circunferencia se obtienen los puntos de
tangencia T’1 y T’2. Ahora hay que deshacer la transformación que hemos realizado
volviendo a sumar R1 a todos los elementos. Los puntos de tangencia obtenidos se
transforman e T1y T2 y serán los puntos de tangencia en la circunferencia de centro O2.
Para obtener los puntos de tangencia en la circunferencia de centro O1 se trazan
paralelas a T1O2 y T2O2 desde O1 para obtener los puntos de tangencia T3 y T4. Basta
unir los puntos de tangencia T3 con T1 y T4 con T2 para tener las tangentes buscadas.
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
11
3.11 Aplicaciones del eje radical en los problemas de tangencias
La principal utilidad de lo visto hasta ahora es su aplicación en la resolución de ciertos
problemas de tangencias, para lo cual se usarán las propiedades explicadas. Lo
importante es comprender él por qué de las construcciones y no memorizarlas.
3.11.1 Circunferencias tangentes a otra y que pasan por dos puntos
Dada una circunferencia de centro O y dos puntos P y Q, se
desea dibujar las circunferencias tangentes a ésta y que
pasen por los puntos (Fig. 21).
O
Q
Al tener que pasar por P y Q, la recta PQ será el eje radical
de todas las circunferencias que pasen por ellos (Fig. 22),
incluidas las que sean tangentes a la circunferencia de centro
O. Y se ha visto además que para un punto del eje radical,
las longitudes de los segmentos tangentes a las
circunferencias que tengan dicho eje radical, serán la misma.
P
La circunferencia de centro O no tiene el eje radical PQ. Se
traza una circunferencia auxiliar cualquiera que pase por P y
Q y corte a la circunferencia de centro O. Esta circunferencia auxiliar corta a la de
centro O en dos puntos A y B, siendo AB el eje radical de ambas.
Fig. 21
T1
M
m
O
B
T2
A
Q
P
Fig. 22 Circunferencias tangentes a otra pasando por 2 puntos
Donde se corten este eje radical y el de las circunferencias que pasen por P y Q (punto
M) cumplirá que la magnitud del segmento tangente a la circunferencia de centro O y a
cualquiera que pase por P y Q (incluidas las tangentes buscadas), es la misma por ser M
intersección de 2 ejes radicales. Luego haciendo las tangentes a la circunferencia de
centro O se tienen T1 y T2, que serán los puntos de tangencia entre las circunferencias
dada y las circunferencias buscadas.
Basta dibujar las circunferencias que pasen por T1, P y Q además de la que pase por T2,
P y Q para tener la solución del problema.
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
12
3.11.2 Circunferencias tangentes a una recta pasando por dos puntos
Dada una recta r y dos puntos P y Q, se desean
trazar las circunferencias tangentes a la recta r y
que pasen por P y Q (Fig. 23).
Q
P
Al tener que pasar por P y Q, la recta PQ será el
eje radical de todas las circunferencias que pasen
Fig. 23
por ellos (Fig. 24), incluidas las que sean
tangentes a la recta r. Y se ha visto que para un
punto del eje radical, las longitudes de los segmentos tangentes a las circunferencias que
tengan dicho eje radical, serán la misma.
r
O2
Q
T
M
P
T2
U
T1
r
Fig. 24 Circunferencias tangentes a una recta pasando por 2 puntos
Los centros de las circunferencias deberán de estar además en la mediatriz del segmento
PQ que pasa por M, punto medio de PQ. Se traza una circunferencia auxiliar que pase
por P y Q. Si desde el punto U, intersección del eje radical PQ y de r, se trazan las
tangentes a la circunferencia auxiliar, la magnitud UT, llevada sobre r nos dará los
puntos de tangencia T1 y T2 sobre r de las circunferencias buscadas.
Basta levantar perpendiculares a r por estos puntos T1 y T2 para tener los centros O1 y
O2 de las circunferencias buscadas.
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
13
3.11.3 Circunferencias tangentes a dos rectas y que pasan por un punto
Dadas dos rectas r y s, que se cortan en este caso,
y un punto P (Fig. 25), para obtener las
circunferencias tangentes a r y s que pasan por P,
se transforma el problema en el del punto10.2 que
ya se ha explicado como resolver.
r
P
Para esto, al pasar la solución por el punto P,
pasará por su simétrico P’ respecto a la bisectriz b
s
de las dos rectas r y s (Fig. 26). El problema se
transforma entonces en trazar las circunferencias
Fig. 25
tangentes a una recta (r ó s) y que pasen por P y
P’, que se resuelve como se explicó en 3.11.2, teniendo el problema dos posibles
soluciones.
r
P
b
P'
s
Fig. 26 Circunferencias tangentes a dos rectas pasando por un punto
3.11.4 Circunferencias tangentes a dos rectas y a otra circunferencia
Dadas dos rectas r y s y una circunferencia
comprendida entre las mismas, de centro O y
radio R (Fig. 27), para tener la solución del
mismo se transforma el problema en el de
dibujar las tangentes a dos rectas pasando por
un punto.
r
R
O
Para ello se “resta” el radio R a todos los
elementos del sistema, con lo que la
circunferencia se transforma en su centro y las
s
dos rectas r y s en dos rectas paralelas a si
Fig. 27
mismas a una distancia R (Fig. 28). El
problema se transforma en dibujar las circunferencias tangentes a las rectas
transformadas r’ y s’ y que pasen por O.
Apuntes de Geometría plana
ETSI Navales
Tema03: Circunferencia
14
Obtenidos los puntos de tangencia T’1 y T’2, se deshace la transformación volviendo a
sumar R, llevándolos sobre las rectas originales r y s para tener los puntos de tangencia
T1 y T2 de las soluciones buscadas sobre las rectas.
Levantando las perpendiculares desde estos puntos de tangencia hasta la bisectriz de las
2 rectas, se tienen los centro O1 y O2 de las circunferencias buscadas.
r
R
r'
O1
O
O2
T'2
T'1
s'
R
T2
T1
s
Fig. 28 Circunferencias tangentes a dos rectas y a otra circunferencia
El problema tiene otras dos soluciones. En el caso anterior (Fig. 28) se ha “restado” R
en una dirección, ahora se “resta” en la dirección contraria (Fig. 29), transformándose
de nuevo la circunferencia en su centro O y las rectas r y s en r’ y s’, paralelas pero en
distinto sentido que en la Fig. 28.
r'
r
b
R
O1
O
O2
T2
T1
R
s
T'1
s'
T'2
Fig. 29 Circunferencias tangentes a dos rectas y a otra circunferencia
El problema genérico tiene por tanto cuatro soluciones como máximo, aunque el
número de soluciones posibles depende de la posición relativa entra las rectas r y s y la
circunferencia de centro O y radio R.
Apuntes de Geometría plana
ETSI Navales