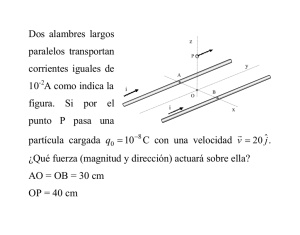
r I B

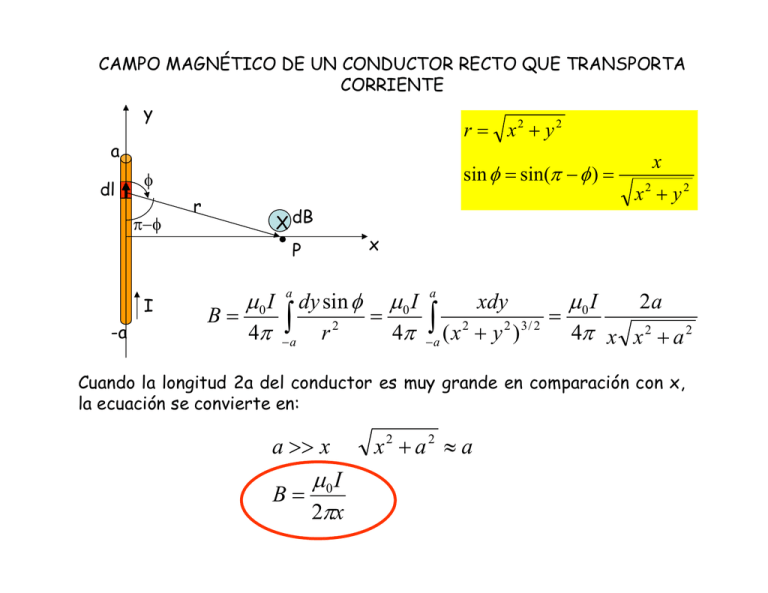
CAMPO MAGNÉTICO DE UN CONDUCTOR RECTO QUE TRANSPORTA
CORRIENTE
y
r = x2 + y2
a
dl
sin φ = sin(π − φ ) =
φ
π−φ
r
-a
x2 + y2
X dB
P
I
x
µ0 I
B=
4π
x
dy sin φ µ0 I
∫−a r 2 = 4π
a
µ0 I
2a
xdy
∫−a ( x 2 + y 2 )3/ 2 = 4π x x 2 + a 2
a
Cuando la longitud 2a del conductor es muy grande en comparación con x,
la ecuación se convierte en:
a >> x
µ0 I
B=
2πx
x2 + a2 ≈ a
I r
I r
µ0 I
B=
2πr
28.12 Un alambre recto y largo yace a lo largo del eje y y transporta una
corriente I=8 A en la dirección –y. Además del campo magnético debido a la
corriente en el alambre, hay un campo magnético uniforme B0 con una
magnitud de 1.5 10-6 T en la dirección +x. ¿Cuál es el campo total en los
puntos siguientes del plano xz?
a) x=0, z=1 m;
a ) BT = B0 − B = 1.5 10 −6 T −
b) x=1m, z=0;
µ0 I
=
2πz
(4π 10 −7 Tm / A)(8 A)
1.5 10 T −
=
2π (1m)
c) x=0, z=-0.25m?
−6
y
(1.5 10 −6 − 1.6 10 −6 )T = −0.1 10 −6 T
B0
c
x
z
I
a
c
I
X
a
b
2
 µ0 I 
 = 2.19 10 −6 T
b) BT = B + B = (1.5 10 T ) + 
 2π (1m) 
2
0
B
b
2
−6
2
28.12 Un alambre recto y largo yace a lo largo del eje y y transporta una
corriente I=8 A en la dirección –y. Además del campo magnético debido a la
corriente en el alambre, hay un campo magnético uniforme B0 con una
magnitud de 1.5 10-6 T en la dirección +x. ¿Cuál es el campo total en los
puntos siguientes del plano xz?
a) x=0, z=1 m;
b) x=1m, z=0;
c) x=0, z=-0.25m?
y
c
x
I
a
c
I
X
a
c) BT = B0 + B = 1.5 10 T +
µ0 I
2π (0.25m)
1.5 10 −6 T + 64 10 −7 T = 7.9 10 −6 T
B0
z
−6
B
b
b
=
28.16 Dos alambres paralelos rectos y largos, separados por una distancia de 10
cm, transportan corrientes iguales, de 4 A en la misma dirección. Proporcione la
magnitud y dirección del campo magnético en:
a) el punto P1, a medio camino entre los alambres;
b) En el punto P2, a 25 cm a la derecha de P1;
1
2
P1
10 cm
25cm
P2
28.17 Dos líneas de transmisión paralelas y largas, separadas 40 cm,
transportan corrientes de 25 A y 75 A. Halle todos los puntos donde el campo
magnético neto de los dos alambres es cero si estas corrientes fluyen a) en el
mismo sentido, b) en sentidos opuestos.
I1=25 A
I2=75 A
a) B es cero en el espacio entre los alambres:
µ 0 I1
µ0 I 2
=
2π (0.4 − x) 2π ( x)
x
0.4m
x
I1 x = I 2 (0.4 − x)
x( I1 + I 2 ) = I 2 (0.4m)
x=
I 2 (0.4m) (75 A)(0.4m)
=
= 0.3m
( I1 + I 2 )
(100 A)
B es 0 a una distancia de 0.3 m a la izquierda de I2
y a una distancia de 0.1 m a la derecha de I1.
28.17 Dos líneas de transmisión paralelas y largas, separadas 40 cm,
transportan corrientes de 25 A y 75 A. Halle todos los puntos donde el campo
magnético neto de los dos alambres es cero si estas corrientes fluyen a) en el
mismo sentido, b) en sentidos opuestos.
I1=25 A
I2=75 A
a) B es cero en el espacio entre los alambres:
µ 0 I1
µ0 I 2
=
2π (0.4 − x) 2π ( x)
x
0.4m
x
I1 x = I 2 (0.4 − x)
x( I1 + I 2 ) = I 2 (0.4m)
x=
I 2 (0.4m) (75 A)(0.4m)
=
= 0.3m
( I1 + I 2 )
(100 A)
B es 0 a una distancia de 0.3 m a la izquierda de I2
y a una distancia de 0.1 m a la derecha de I1.
28.17 Dos líneas de transmisión paralelas y largas, separadas 40 cm,
transportan corrientes de 25 A y 75 A. Halle todos los puntos donde el campo
magnético neto de los dos alambres es cero si estas corrientes fluyen a) en el
mismo sentido, b) en sentidos opuestos.
I1=25 A
I2=75 A
b) B puede ser cero a la izquierda de I1 y a la
derecha de I2:
µ 0 I1
µ0 I 2
=
2π ( x) 2π ( x + 0.4m)
x
0.4m
x
I1 ( x + 0.4m) = I 2 x
x( I1 − I 2 ) = − I1 (0.4m)
x=
− I1 (0.4m) (−25 A)(0.4m)
=
= 0.2m
( I1 − I 2 )
(−50 A)
B es 0 a una distancia de 0.2 m a la izquierda de I1
y a una distancia de 0.6 m a la derecha de I2.
FUERZA ENTRE CONDUCTORES PARALELOS
L
I2
B1
I1
F
r
Consideremos dos alambres que conducen
corrientes I1 y I2. El conductor de abajo
genera un campo magnético B, que en la
posición del conductor de arriba, tiene
magnitud:
B1 =
µ 0 I1
2πr
La fuerza que este campo ejerce sobre un tramo de longitud L del
r r
conductor superior es:
F = I 2 L × B1
B es perpendicular al conductor superior, entonces:
F = I 2 LB1 = I 2 L
F µ 0 I1 I 2
=
L
2πr
µ 0 I 1 µ 0 I1 I 2 L
=
2πr
2πr
Hacia abajo
Fuerza por unidad de longitud
FUERZA ENTRE CONDUCTORES PARALELOS
I2
r
I1
F
L
La corriente del conductor superios también
crea un campo magnético en la posición del
conductor de abajo.
µ0 I 2
B2 =
2πr
B2
La fuerza que este campo ejerce sobre un tramo de longitud L del
conductor inferior es:
r r
F = I1 L × B2
B es perpendicular al conductor inferior, entonces:
F = I1 LB2 = I1 L
µ 0 I 2 µ 0 I1 I 2 L
=
2πr
2πr
Hacia arriba
I1
I1
I2
I2
Dos conductores paralelos que transportan
corriente en el mismo sentido se atraen
mutuamente
Dos conductores paralelos que transportan
corriente en sentidos opuestos se repelen
mutuamente
DEFINICIÓN DE AMPERE
Un ampere es la corriente que, si está presente en dos conductores
paralelos de longitud infinita y separados por una distancia de un metro en
el espacio vacío, provoca que cada conductor experimente una fuerza de
exactamente 2 10-7 N por metro
F µ 0 I1 I 2
=
L
2πr
28.22 Dos alambres paralelos y largos están separados por una distancia de
0.4 m. Las corrientes I1 e I2 tienen los sentidos que se indican.
a) Calcule la magnitud de la fuerza que cada alambre ejerce sobre un tramo
de 1.2 m del otro. ¿Es la fuerza de atracción o de repulsión?
b) Se duplican las dos corrientes, de modo que I1 es ahora de 10 A e I2 de 4
A. ¿Cuál es ahora la magnitud de la fuerza que cada alambre ejerce sobre
un tramo de 1.2 m del otro?
I1=5 A
0.4 m
I2=2 A
a)
µ0 I1 (2 10 −7 Tm / A)(5 A)
=
= 2.5 10 −6 T
B1 =
2πd
0.4m
µ0 I 2 (2 10 −7 Tm / A)(2 A)
=
= 10 −6 T
B2 =
2πd
0.4m
F1 = I1 LB2 = (5 A)(1.2m)(10 −6 T ) = 6 10 −6 F2 = I 2 LB1 = (2 A)(1.2m)(2.5 10 −6 T ) = 6 10 −6 repulsive
28.22 Dos alambres paralelos y largos están separados por una distancia de
0.4 m. Las corrientes I1 e I2 tienen los sentidos que se indican.
a) Calcule la magnitud de la fuerza que cada alambre ejerce sobre un tramo
de 1.2 m del otro. ¿Es la fuerza de atracción o de repulsión?
b) Se duplican las dos corrientes, de modo que I1 es ahora de 10 A e I2 de 4
A. ¿Cuál es ahora la magnitud de la fuerza que cada alambre ejerce sobre
un tramo de 1.2 m del otro?
I1=5 A
0.4 m
I2=2 A
b)
(2 10 −7 Tm / A)(10 A)(4 A)(1.2m)
µ 0 I1 I 2
= 2.4 10 −5 F=
L=
2πd
0.4m
CAMPO MAGNÉTICO DE UNA ESPIRA CIRCULAR DE CORRIENTE
y
Consideremos un conductor circular de radio a
que transporta una corriente I. Con la ley de
Biot-Savart se puede hallar el campo magnético
en un punto P sobre el eje x a una distancia x del
centro de la espira.
dl
a θ
I
z
I
I
r dBy
dB
θ
P dB
x
x
x
sin(θ ) = =
r
(x2 + a2 )
cos(θ ) =
a
a
=
r
(x2 + a2 )
x
dl
µ0 I
4π ( x 2 + a 2 )
µ0 I
dl
a
dBx = dB cos(θ ) =
4π ( x 2 + a 2 ) ( x 2 + a 2 )
µI
dl
x
dB y = dB sin(θ ) = 0
4π ( x 2 + a 2 ) ( x 2 + a 2 )
dB =
Por simetría, por cada elemento dl hay un elemento correspondiente
en el lado opuesto de la espira, que crea una componente dBy en
dirección opuesta, entonces By=0
CAMPO MAGNÉTICO DE UNA ESPIRA CIRCULAR DE CORRIENTE
y
dl
a
µ0 I
4π ( x 2 + a 2 ) ( x 2 + a 2 )
adl
µI
µ 0 Ia
dl
Bx = ∫ 0
=
2
2 3/ 2
2
2 3/ 2 ∫
4π ( x + a )
4π ( x + a )
dBx = dB cos(θ ) =
dl
a θ
I
z
I
I
r dBy
dB
θ
P dB
x
x
x
sin(θ ) = =
r
(x2 + a2 )
a
a
cos(θ ) = =
r
(x2 + a2 )
x
Bx =
µ0 Ia
4π ( x + a )
2
2 3/ 2
2πa =
µ0 Ia 2
2( x 2 + a 2 ) 3 / 2
En el centro de la espira (x=0):
Bx =
µ0 I
2a
Si en lugar de una espira es una bobina de N
espiras:
Bx =
µ 0 I
2a