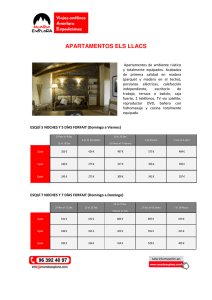
Frecuencia de resonancia (wr) y valor pico de resonancia

IDENTIFICACIÓN DE LA FUNCION DE TRANSFERENCIA
USANDO EL DIAGRAMA DE BODE
Determinación de la función de transferencia de lazo abierto de un sistema a
partir de la curva asintótica de magnitud del Diagrama de Bode.
Determinación del error estacionario de un sistema de lazo cerrado.
Se puede determinar el tipo del sistema, la ganancia de lazo abierto y las
frecuencias de cruce de lazo abierto.
Sistema Tipo 0
Lm, dB
K0
1 + jωTa
G ( jω) =
Para K0 > 1
20 log K0
-20dB/dec
0
1 / Ta
En ω <
1
Ta
ω=
En
1
Ta
Lm G(jω) = 20 log K0
frecuencia de cruce
⇒
Pendiente de la curva de magnitud logarítmica es cero por debajo de la
frecuencia de cruce y -20dB/dec por encima de la frecuencia de cruce.
Para un sistema Tipo 0, las características son:
1. La pendiente a bajas frecuencias es cero.
2. La magnitud a bajas frecuencias es de 20 log K0.
3. La ganancia K0 es el coeficiente estático de posición.
Sistema Tipo 1
K1
jω(1 + jωTa )
G ( jω) =
Lm, dB
Lm, dB
20logK1
-20dB/dec
0
ωx=K1
ω = 1 ω1
1
> K1
Ta
En ω <
-40dB/dec
ω1
1
< K1
Ta
ω=1
ωx=K1
1
LmG(jω) = Lm K1 – Lm jω pendiente de -20dB/dec
Ta
En ω = K1 LmG(jω)ω=K1 = 0
En ω = 1
0
ω
20logK1
LmG(jω)ω=1 = 20 log K1
gráfica de
K1
cruza 0 dB en ω = K1
jω
frecuencia ωx < ó > 1 dependiendo
si K1 < ó > 1.
Para un sistema Tipo 1 las características son:
1. La pendiente a bajas frecuencias es de -20dB/dec.
2. La interceptación de la pendiente de –20 dB/dec (o su extensión) con el
eje a 0 dB ocurre en la frecuencia ωx, donde ωx = K1.
3. El valor de la pendiente de –20 dB/dec (o su extensión) en la frecuencia
ω = 1 es igual a 20 log K1.
4. La ganancia K1 es el coeficiente estático de velocidad.
ω
Sistema Tipo 2
G ( jω) =
Lm, dB
K2
( jω) 2 (1 + jωTa )
Lm, dB
-40dB/dec
0
ω=1
ωy
ω1
ω
ω1
0
ωy
ω=1
ω
20logK2
20logK2
-60dB/dec
1
> K2
Ta
En ω <
1
Ta
En ω2 = K2
1
< K2
Ta
ω y =K 2
2
ω y =K 2
2
LmG(jω) = Lm K2 – Lm (jω)2 pendiente de -40dB/dec
LmG(jω) = 0
La interceptación de la pendiente inicial de 40dB/dec (o su extensión) con el eje a 0dB
ocurre en la frecuencia ωy ⇒ ωy2 = K2
En ω = 1 LmG(jω)ω=1 = 20 log K2 Este punto ocurre en la pendiente inicial
o su extensión, dependiendo de si
ω1 =
1
es mayor o menor que
Ta
K2
Si K2 > 1, 20 log K2 > 0
Si K2 < 1, 20 log K2 < 0
Para un sistema Tipo 2, las características son:
1. La pendiente a bajas frecuencias es de -40dB/dec.
2. La interceptación de la pendiente de -40dB/dec (o su extensión) con el
eje a 0 dB ocurre en la frecuencia ωy, donde ωy2 = K2.
3. El valor de la pendiente a baja frecuencia de -40dB/dec (o su extensión)
en la frecuencia ω = 1 es igual a 20 log K2.
4. La ganancia K2 es el coeficiente estático de aceleración.
RELACION ENTRE LA RESPUESTA TRANSITORIA DE LAZO
CERRADO Y LA RESPUESTA FRECUENCIAL DE LAZO CERRADO
Sistema estable y bien
amortiguado
Sistema estable pero
oscilatorio
Sistema
marginalmente
estable
Sistema
inestable
FRECUENCIA DE RESONANCIA (ωR) Y VALOR PICO DE
RESONANCIA
G ( jω) =
G ( jω) =
1
ω ⎛ ω⎞
+⎜j ⎟
1 + 2ξj
ωn ⎜⎝ ωn ⎟⎠
1
2
2
2 ⎞
⎛
⎜1 − ω ⎟ + ⎛⎜ 2ξ ω
⎜ ω 2⎟ ⎜ ω
⎝
n
⎝
n ⎠
⎞
⎟⎟
⎠
2
Para ξ < 1 el Ln⏐G(jω)⏐ tiene un valor pico
Se produce valor pico de ⏐G(jω)⏐ cuando
2
⎛
⎛
ω
ω2 ⎞⎟
⎜
g (ω) = 1 −
+ ⎜⎜ 2ξ
⎜ ω 2⎟
⎝ ωn
⎝
n ⎠
(
2
⎞ ⎡ ω 2 − ω n 2 1 − 2ξ 2
⎟⎟ = ⎢
ωn 2
⎠ ⎢⎣
Valor mínimo se produce en ω r = ω n 1 − 2ξ 2
Mr = G ( jω) max =
)⎤⎥ 2 + 4ξ2 (1 − ξ2 )
⎥⎦
→
(0 ≤ ξ ≤ 0.707)
1
2ξ 1 − ξ 2
Ángulo de fase en la frecuencia de resonancia
⎡
ω ⎤
⎥
⎢ 2ξ
2
ω
ξ
⎥
−1 ⎢
−1 1 − 2ξ
−1
n
φ = − tan ⎢
=
−
tan
=
−
90
°
+
sen
2⎥
ξ
1 − ξ2
⎢1 − ⎛⎜ ω ⎞⎟ ⎥
⎢ ⎜⎝ ωn ⎟⎠ ⎥
⎦
⎣
MINIMO
Máximo pico de
resonancia
de un sistema de
2do orden a lazo
cerrado
RESPUESTA DE SISTEMAS DE SEGUNDO ORDEN
SUBAMORTIGUADOS
Frecuencia:
ωr = ωn 1 − 2ζ 2
1
Mr =
2ζ 1 − ζ 2
ωr es real sólo cuando ξ<0,707
Tiempo:
1.5
Mp
1
0.9
0.5
0.1
0
tr
tc
tp 1
2
3
4
(1 + 0.6ξ + 015
. ξ2 )
tr =
ωn
tp =
π
ωn 1 − ξ2
Mp % =
( )
=
c t p − c(∞ )
c(∞ )
π
ωd
t c = t 90% − t10%
ts =
3
ξω
1 + 11
. ξ + 14
. ξ2
=
ωn
ts =
4
ξω
2
⎛
⎞
× 100 = ⎜ e − πξ / 1−ξ ⎟ × 100
⎝
⎠
• ωr es indicativo de la velocidad de respuesta de un sistema.
↓ξ ↑ωr ↑ωd ↓tr ⇒ sistema más rápido.
ξ→0
⇒
Mr → ∝
Mp → 1
ωc (odb) > ωn > ωr
También se cumple que la ωr’ > ωr donde ωr’ es la de lazo cerrado.
•
Mr es un indicativo de estabilidad del sistema.
Comportamiento satisfactorio se obtiene cuando:
1 < Mr < 1,4 ó (0db<Mr<3db)
el cual corresponde a:
0,4 < ξ < 0,7
Gráficas de Mr
en función de ξ
y de Mp en
función de ξ
Cuando
ξ→0
Cuando ξ > 0.4
Mr → ∝
Mp → 1
Mas grandes
son los valores
de Mp y Mr
Relación estrecha entre Mr y Mp
ANCHO DE BANDA
Se define como la frecuencia a la cual la magnitud de la FTLC cae 70,7%
de su nivel a bajas frecuencias o 3 db por debajo de la ganancia a cero db.
db
0
-3
BW
ω
Da una medida de la respuesta en tiempo
↑ BW ⇒ tr rápido ⇒ sistema rápido
Sigue mejor la perturbación al sistema pero produce ↑ Mp y pasa
fácilmente los ruidos
↓ BW ⇒ tr lento ⇒ sistema lento
Obtención
- Se puede obtener gráficamente
- Se puede obtener igualando la magnitud de la FTLC = 0,707 y
despejar
Para un sistema de 2° orden
(1 − 2ζ ) +
BW = ω n
2
4ξ 4 − 4ξ 2 + 2
De la gráfica de respuesta transitoria
Si ↑ξ ↑tr ⇒ sistema más lento
De la gráfica de respuesta Ancho de Banda
Si ↑ξ ↑tr ↓ BW⇒ sistema más lento
Si ↓ξ ↓tr ↑ BW⇒ sistema más rápido
BW =
BW =
4
(1 − 2ξ ) +
4ξ 4 − 4ξ 2 + 2
2
t ss ξ
4
tp 1− ξ
(1 − 2ξ ) +
2
4ξ 4 − 4ξ 2 + 2