Criterios de divisibilidad, (2, 3, 5, 7 y 11)
Anuncio

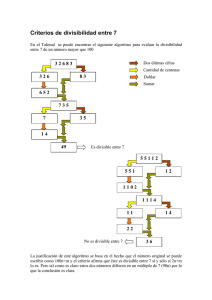
Matemáticas - 1o ESO 1 Criterios de divisibilidad, (2, 3, 5, 7 y 11) Existen unos procedimientos, algunos muy sencillos, para determinar si un número es divisor de otros o no. Estudiamos aquı́ los criterios de divisibilidad para algunos de los primeros números. • Divisibilidad por 2 Todo número par, (terminado en 0, 2, 4, 6 u 8), es divisible por 2. Ejemplos: 18 y 542 son divisibles por 2, (terminan en 8 y 2, pares). 13 y 27 no son divisibles por 2, (terminan en cifras impares). • Divisibilidad por 3 Un número es divisible por 3 si la suma de sus dı́gitos es divisible por 3. Ejemplos: 1275 es divisible por 3, ya que 1+2+7+5=15, divisible por 3. 1327 no es divisible por 3, ya que 1+3+2+7=19, que no es divisible por 3. • Divisibilidad por 5 Un número es divisible por 5 si termina en 0 o en 5. Ejemplos: 1275 es divisible por 5, ya que termina en 5. 1327 no es divisible por 5, ya que no termina ni en 0 ni en 5. • Divisibilidad por 7 Un número es divisible por 7 si la diferencia entre dicho número sin las unidades y el doble de las unidades es 0 o múltiplo de 7. Ejemplos: – 119 es divisible por 7, ya que la diferencia entre el número sin las unidades, (11), y el doble de las unidades, (9 · 2 = 18), es 18-11=7, múltiplo de 7. – 126 es divisible por 7, ya que la diferencia entre el número sin las unidades, (12), y el doble de las unidades, (6 · 2 = 12), es 0, (12-12=0). – 76 no es divisible por 7, ya que la diferencia entre el número sin las unidades, (7), y el doble de las unidades, (6 · 2 = 12), es 12-6=6, que no es ni 0 ni múltiplo de 7. Si el número es grande, puede aplicarse varias veces el método. Ejemplo: 2625 será divisible entre 7 si 262 − 5 · 2 = 262 − 10 = 252 es divisible entre 7. 252 es divisible entre 7, ya que 25 − 2 · 2 = 25 − 4 = 21 es divisible entre 7. Por tanto, 2625 es divisible entre 7. www.EsoBachilleratoUniversidad.Com.Es Matemáticas - 1o ESO 2 • Divisibilidad por 11 Un número es divisible por 11 si la diferencia entre la suma de sus dı́gitos pares y la suma de sus dı́gitos impares es cero o múltiplo de 11. Al igual que en el criterio para el 7, es posible que el método deba aplicarse varias veces. Ejemplos: – 12914 es divisible por 11, ya que la diferencia entre la suma de sus dı́gitos impares, (1+9+4=14) menos la suma de sus dı́gitos pares, (2+1=3), es (14-3=11) múltiplo de 11. – 37697 es divisible por 11, ya que la diferencia entre la suma de sus dı́gitos impares, (3+6+7=16) menos la suma de sus dı́gitos pares, (7+9=16), es cero, (16-16=0). – 126 no es divisible por 11,, ya que la diferencia entre la suma de sus dı́gitos impares, (1+6=7) menos la suma de sus dı́gitos pares, (2), es 1, (7-2=5), que no es ni 0 ni múltiplo de 11. Criterios de divisibilidad, (4, 6, 8, 9 y 10) Los criterios de divisibilidad que hemos visto anteriormente corresponden a los primeros números primos, (concepto que ampliaremos en siguientes apartados), y son básicos en matemáticas. Pero también es útil conocer los criterios para otros números. Expondremos a continuación los criterios para los números que nos faltan hasta el 10. • Divisibilidad por 4 Un número es divisible por 4 si sus 2 últimas cifras son 00, o múltiplo de 4. Además, para ser divisible por 4 tiene que ser divisible por 2, con los que todos los impares quedan descartados. Ejemplos: – 48300 es divisible por 4, ya que termina en 00. – 6792 es divisible por 4, ya que 92 = 23 · 4 es divisible por 4. – 1263 no es divisible por 4, ya que es impar. • Divisibilidad por 6 Un número es divisible por 6 si es divisible por 2 y por 3. Ejemplos: – 6792 es divisible por 6, ya que es par, (divisible por 2) y sus dı́gitos suman 6+7+9+2=24, múltiplo de 3. www.EsoBachilleratoUniversidad.Com.Es Matemáticas - 1o ESO 3 – 1262 no es divisible por 6, ya que aunque es par, la suma de sus dı́gitos, (1+2+6+2=11), no es múltiplo de 3. • Divisibilidad por 8 Un número es divisible por 8 si sus tres últimos dı́gitos son 000, o múltiplos de 8. Además tiene que ser múltiplo de 2, con lo que los impares quedan descartados. Ejemplos: – 882000 es divisible entre 8, ya que termina en 000. – 9872 es divisible por 8, ya que 872 = 109 · 8. – 126122 no es divisible por 8, ya que 122:8=15, con resto 2. • Divisibilidad por 9 Un número es divisible por 9 si la suma de sus dı́gitos es divisible entre 9. Ejemplos: – 156312 es divisible por 9, ya que 1 + 5 + 6 + 3 + 1 + 2 = 18, divisible entre 9. – 12612 no es divisible por 9, ya que 1+2+6+1+2=12, que no es divisible entre 9. • Divisibilidad por 10 Un número es divisible por 10 si acaba en 0. Ejemplo: 56310 es divisible por 10, ya que acaba en 0. www.EsoBachilleratoUniversidad.Com.Es