Ejercicios de Estatica

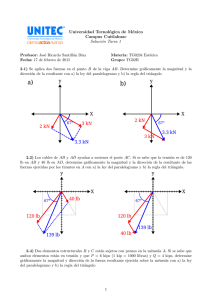
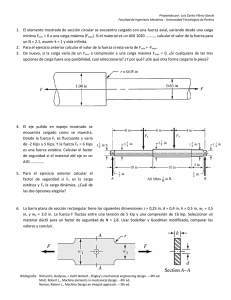
ESTATICA
Problema 6.11. Armadura Howe: Determine la fuerza en cada uno de los miembros de la
armadura Howe para techo mostrada en la figura.
6KN
D
6m
6KN
6KN
B
F
6m
3KN
3KN
C
A
8m
G
E
8m
Diagrama de cuerpo libre:
8m
H
8m
6KN
D
6m
6KN
6KN
B
F
6m
3KN
3KN
C
A
G
E
H
FA
FHX
FHY
8m
8m
8m
8m
Aplicando momento en H:
ΣMH=0
-FA x 32m + 3KN x 32m+6KN x (24m+16m+8m) = 0
-FA X 32m + 96 KN + 6 KN x 48m = 0
384KN
FA x 32m = 96 KN + 288 KN ⇒
FA =
32m
FA = 12 KN
ΣFY=0
- 3KN + 12KN – 6KN x 3 – 3 KN + FH = 0
FH = 12 KN
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 1 de 26
ESTATICA
Análisis Nodo A:
3KN
FAB
ΣFY=0
6
8
A
12KN – 3KN – FAB x
FAC
FAB x
12KN
6
=0
10
6
10x9
= 9 KN ⇒ FAB =
10
6
FAB = 15 KN C .
ΣFX=0
FAC - FAB
8
8
15KNx8
= 0 ⇒ FAC = FAB
=
10
10
10
FAC = 12 KN T
Análisis Nodo C:
FCB
FCE
FAC
C
Por Teoría se puede decir que este nodo esta bajo
condiciones especiales de carga, este conecta tres
elementos, dos de los cuales se encuentran en la misma
línea y no están sujetos a cargas externas, por tanto FCB=0
y FAC = FCE
FAC = FCE = 12 KN T
FCB = 0 KN
.
Análisis Nodo G:
FGF
FGH
FEG
G
El análisis de este nodo es idéntico al del nodo C, FGF = 0
y FGH = FEG, entonces podemos decir que por simetría,
FAC = FCE = FGH = FEG = 12 KN T
FGF = 0 KN
.
Análisis Nodo B:
FBE
FBD
6
6
8
B
6
8
FAB
6KN
8
ΣFY=0
6
6
6
+ FBE x
- 6 KN + FBD x
=0
10
10
10
6
6
FBE x
+ FBD x
= -3 KN . . . (E1)
10
10
15KN x
ΣFX=0
8
8
8
- FBE x
+ FBD x
=0
10
10
10
8
8
- FBE x
+ FBD x
= - 12 KN . . . (E2)
10
10
15KN x
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 2 de 26
ESTATICA
 8
Multiplicamos E1 por  −  y sumamos a E2 para obtener el FBE
 6
8
8
 8
- FBE x
E1 x  −  + E2:
- FBD x
= 4 KN
10
10
 6
8
8
- FBE x
+ FBD x
= - 12KN
10
10
8
- FBE x
+
0
=-8
5
5
FBE = 8 x
8
FBE = 5 KN C
Sustituimos el valor de FBE en E1 para así obtener el valor de FBD.
5KN x
6
6
6
10
+ FBD x
= - 3 KN ⇒ FBD x
= -3 KN – 3KN ⇒ FBD = - 6 KN x
10
10
10
6
FBD = 10 KN C
Análisis Nodo F:
Para el análisis de este nodo se puede decir que por simetría,
FBE = FEF = 5KN C .
FBD = FDF = 10KN C
Análisis Nodo E:
ΣFY=0
FED
FBE
FEF
6
FCE
8
8
6
6
6
+ FDE x
-5x
=0
10
10
10
6
FDE = 10KN x
10
- 5KN x
6
FEG
FDE = 6 KN T
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 3 de 26
ESTATICA
Problema 6.6: Determine la fuerza en cada uno de los miembros de la armadura mostrada
en la figura.
9Kips
B
6ft
C
A
6ft
D
3Kips
8ft
17,5ft
Diagrama de cuerpo libre:
9.9 Kips
B
6ft
C
A
RAX
6ft
D
RAY
3Kips
8ft
RC
17,5ft
Aplicando momento en A:
ΣMA=0
RC x 25,5ft + 3Kips x 6ft -9,9Kips x 8ft = 0
RC x 25,5ft = 79,2 Kips – 18 Kips
61,2 Kips
RC x 25,5ft = 61,2 Kips ⇒ RC =
25,5 ft
RC = 2,4 Kips
ΣFY=0
RAY + RC – 9,9 Kips = 0
RAY = 9,9 Kips – 2,4 Kips
RAY = 7,5 Kips
ΣFX=0
RAX + 3 Kips = 0
RAX = 3 Kips
.
Análisis Nodo A:
ΣFY=0
RAY
6
6
– TAB x
=0
10
10
6
6
- TAD x
- TAB x
= - 7,5 Kips . . . (E1)
10
10
RAY – TAD x
A
RAX
6 6
TAB
8
8
TAD
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 4 de 26
ESTATICA
ΣFX=0
8
8
- TAB x
= 0
10
10
8
8
TAD x
- TAB x
= 3 Kips . . . (E2)
10
10
- RAX + TAD x
8
Multiplicamos E1 por   y sumamos a E2 para obtener el TAD
6
8
8
8
E1 x   + E2:
- TAD x
- TAB x
= - 10 Kips
10
10
6
8
8
TAD x
- TAB x
= 3 Kips
10
10
8
0
- TAB x
= - 7 Kips
5
5
TAB = 7 Kips x
8
TAB = 4,375 Kips C
Sustituimos el valor de TAB en E1 para así obtener el valor de TAD.
6
6
6
- TAD x
- 4,375 Kips x
= - 7,5 Kips ⇒ - TAD x
= -7,5 Kips + 2,625 Kips
10
10
10
10
TAD = 4,875 Kips x
6
TAD = 8,125 Kips T
Análisis Nodo B:
ΣFX=0
9,9Kips
TAB
6
B
8
6
17,5 TBC
TBD
4,375Kips x
8
17,5
=0
– TBC x
10
18,5
17,5
= 3,5 Kips
18,5
18,5
- TBC = 3,5 Kips x
17,5
- TBC x
TBC = 3,7 Kips C
ΣFY=0
6
6
+ 3,7 Kips x
- TBD= 0
10
18,5
TBD = - 9,9 Kips + 2,625 Kips + 1,2 Kips
- 9,9 Kips + 4,375 Kips x
TBD = 6,075 Kips C
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 5 de 26
ESTATICA
Análisis Nodo C:
ΣFX=0
17,5
17,5
- TCD x
=0
18,5
18,5
17,5
TCD x
= 3,5 Kips
18,5
18,5
TCD = 3,5 Kips x
17,5
3,7 Kips x
C
TCD
6 6
17,5 17,5 TBC
RC
TCD = 3,7 Kips T
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 6 de 26
ESTATICA
Problema 6.7: Determine la fuerza en cada uno de los miembros de la armadura mostrada
en la figura.
2,5m
B
A
3m
C
3m
D
E
480 N
Diagrama de cuerpo libre:
FAY
2,5m
B
FAX
A
3m
C
3m
FDX
D
E
480 N
Aplicando momento en A:
ΣMA=0
FDX x 6m = 0
FDX = 0 N
ΣFY=0
- FAY – 480 N = 0
FAY = 480 N .
ΣFX=0
FDX + FAX = 0
FAX = - FDX
FAX = 0 N
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 7 de 26
ESTATICA
Análisis Nodo A:
Hacemos un triangulo de fuerzas:
FAY
FAB
A
FAC
FAB
3
1,25
1,25
480 N
=
3,25
3
FAC
Decimos que:
F
480 FAB
=
= AC = 0
3
1,25 3,25
FAB
F
= AC = 160
1,25 3,25
FAB = 160 x 1,25
;
FAC = 160 x 3,25
FAB = 200 N C
FAC = 520 N T
Ahora por simetría decimos que,
FAC = FCD = FBC = FCE = 200 N C
FAB = FDE = 520 N T
Análisis Nodo B:
FBE
ΣFY=0
3
= 0
3,25
3
TBE = 520 N x
3,25
FBE – TBC x
FAB
B
3
FBC 1,25
TBE = 480 N C
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 8 de 26
ESTATICA
Problema 6.11. Armadura Howe: Determine la fuerza en cada miembro de la armadura
Fink para techo mostrada en la figura.
12Kips
4,5ft
4,5ft
D
12Kips
12Kips
2ft
F
B
6Kips
6Kips
2ft
E
C
A
G
6ft
6ft
6ft
Diagrama de cuerpo libre:
12Kips
4,5ft
4,5ft
D
12Kips
12Kips
2ft
F
B
6Kips
6Kips
2ft
E
C
FAX
G
A
FAY
6ft
6ft
6ft
FG
Aplicando momento en A:
ΣMA=0
-12Kips x (4,5ft + 9ft + 13,5ft) – 6Kips x 18ft + FG x 18ft = 0
FG x 18ft = 12 Kips x 27 ft + 108 Kips
432Kips
FG x 18ft = 324 Kips + 108 Kips
⇒
FG =
18ft
FG = 24 Kips
ΣFY = 0
- 6Kips – 12Kips x 3 – 6Kips + 24Kips + FAY = 0
FAY = 6 Kips + 36 Kips + 6 Kips – 24 Kips
ΣFX = 0
FAY = 24 Kips
⇒ FAX = 0
FAX = 0 Kips
Análisis Nodo A:
6Kips
FAB
A
2
4,5
FR = 24Kips - 6Kips = 18 Kips
Hacemos un triangulo de fuerzas:
FAC
FAC
FAB
4,5
FR
=
4,92
2
FAY = 24Kips
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 9 de 26
ESTATICA
Decimos que:
FAB FAC FR
=
=
=0
4,92 4,5 2
FAB FAC
=
=9
4,92 4,5
FAB = 9 x 4,92
;
FAC = 9 x 4,5
FAB = 44,28 Kips C
FAC = 40,50 Kips T
Ahora, por simetría tenemos que,
FAC = FEG = 40,50 Kips T
FAB = FGF = 44,28 Kips C
Análisis Nodo B:
ΣFX=0
4,5
1,5
4,5
+ FBC x
- FBD x
=0
4,9
2,5
4,9
B
4,5
1,5
4,5
FBC x
- FBD x
= - 40,66 Kips . . . (E1)
22
2,5
4,9
4,5 1,5 FBC
FBD
ΣFY=0
12Kips
2
2
2
-12Kips + 44,28Kips x
- FBC x
- FBD x
=0
4,9
2,5
4,9
2
2
- FBC x
- FBD x
= - 6,07 Kips . . . (E2)
2,5
4,9
Despejamos E1 y E2 para dejarla en función de FBC.
FAB
2
44,28Kips x
1,5
4,5
2,5
4,5 2,5
= - 40,66 Kips + FBD x
⇒ FBC = - 40,66Kips x
+ FBD x
x
2,5
4,9
1,5
4,9 1,5
11,25
FBC = - 67,77 Kips + FBD x
. . . (E1)
7,35
FBC x
2
2
2
2,5
2,5
= FBD x
- 6,07 Kips ⇒ - FBC = FBD x
x
- 6,07 Kips x
2,5
4,9
4,9
2
2
5
FBC = - FBD x
+ 7,58 Kips . . . (E2)
9,8
- FBC x
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 10 de 26
ESTATICA
Igualamos Ecuaciones y despejamos FBD,
11,25
5
- 67,77 Kips + FBD x
= - FBD x
+ 7,58 Kips
7,35
9,8
11,25
5
 11,25 5 
+ - FBD x
= 75,35 Kips ⇒ FBD x 
+
 = 75,35 Kips
7,35
9,8
 7,35 9,8 
75,35 Kips
FBD x 2,04 = 75,35 Kips ⇒ FBD =
2,04
FBD = 36,93 Kips C
FBD x
Sustituimos FBC en E1 para así obtener el valor de FBC,
1,5
4,5
FBC x
- 36,93 Kips x
= - 40,66 Kips
2,5
4,9
1,5
2,5
FBC x
= - 40,66 Kips + 33,94 Kips ⇒ FBD = - 6,72 Kips x
2,5
1,5
FBC = 11,2 Kips C
Por simetría decimos que,
FBD = FDF = 36,93 Kips C
FBC = FEF = 11,2 Kips C
Análisis Nodo C:
ΣFY=0
- 11,2 Kips x
C
FCD x
FAC
FCE
4 2
FCD
3
1,5 FBC
2
4
- FCD x
=0
2,5
5
4
5
= - 8,96 Kips ⇒ FCD = - 8,96 Kips x
5
4
FCD = 11,2 Kips T
ΣFX=0
1,5
3
+ 11,2 Kips = 0
2,5
5
FCE = 40,50 Kips + 6,72 Kips – 6,72 Kips
- 40,50Kips + FCE - 11,2 Kips x
FCE = 40,50 Kips T
Por simetría decimos que,
FCD = FDE = 11,2 Kips T
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 11 de 26
ESTATICA
EJERCICIO 6.1 (PROPUESTO)
Con el método de los nodos, determine la fuerza en cada elemento de la
armadura mostrada en la figura. Para cada elemento establezca se este se
encuentra en tensión o en compresión.
315 N
A
3m
B
C
1.25 m
4m
Cuerpo Libre:
315 N
A
3m
Bx
B
C
By
4m
RC
1.25 m
+ ∑ MB = 0
-315 N * 4 m + RC * 5.25 m = 0
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 12 de 26
ESTATICA
RC = (315 N * 4 m) / 5.25 m
→
RC = 240 N
∑ Fx = 0
∑ Fy = 0
By + RC – 315 N = 0
→
By = 315 N – RC
By = 315 N – 240 N
→
By = 75 N
Análisis del Nodo C
FCA
FCA
RC
CA
3
C
FCB
1.25 m
FCB
RC
Calculo de CA.
CA2 = (3 m)2 + (1.25 m)2 →
CA = 3.25 m
Aplicando la Ley del Seno
RC
FCA
=
3m
FCB
=
3.25 m
1.25 m
FCA = (RC * 3.25 m) / 3m
→
FCA = (240 N * 3.25 m) / 3 m
FCA = 260 N
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 13 de 26
ESTATICA
→
FCB = (RC * 1.25 m) / 3 m
FCB = (240 N * 1.25 m) / 3 m
FCB = 100 N
Análisis del Nodo B.
FBA
5
FBx
B
3
4
FBC
RC
Calculo de Medida BA.
BA2 = (3 m)2 + (4 m)2
→
BA = 5 m
+ ∑ Fx = 0
FBA * 3/5 m + FBy = 0
FBA = (- FBy * 5 m) / 3 m
FBA = -125 N
→
FBA = (-75 N * 5 m) / 3 m
FBA = 125 N
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 14 de 26
ESTATICA
Con el uso del método de los nodos, determine la fuerza en cada uno de los
nodos de los elementos de la armadura mostrada.
2000 lb
1000 lb
12 ft
A
B
12 ft
C
8 ft
D
6 ft
E
12 ft
6 ft
Solución:
Cuerpo Libre:
2000 lb
1000 lb
12 ft
A
B
Cy
12 ft
C
Cx
8 ft
D
E
RE
6 ft
12 ft
6 ft
+ ΣMc = 0
2.000lb*24 ft + 1.000 lb*12 ft – RE*6 ft = 0
RE= (2.000 lb*24 ft + 1.000*12 ft) / 12 ft → RE = 10.000 lb
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 15 de 26
ESTATICA
+ ↑ ΣFy = 0
- 2.000 lb – 1.000 lb + 10.000 lb + Cy = 0
Cy = 2.000 lb + 1.000 lb – 10.000 lb
→
Cy = - 7.000 lb
Cy = 7.000 lb
↓
Análisis nodo A
2.000 lb
FAB
A
4
FAD
2.000 lb
5
5
4
FAB
3
3
FAD
Aplicando La Ley del Seno:
2.000 lb
_
=
4
FAB
FAD
=
3
5
FAB = ( 2.000 lb * 3 ft) / 4 ft
→
FAB = 1.500 LB
FAD = ( 2.000 lb * 5 ft) / 4 ft
→
FAD = 2.500 LB
Análisis nodo D
2.500 lb
FDB
A
FDE
FDE
2.500 lb
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
3
FDB
5
5
Pagina 16 de 26
ESTATICA
Aplicando La Ley del Seno:
2.500 lb
_
=
5
FBD
FDE
=
5
3
FBD = (2.500 lb * 5 ft) / 5 ft
→
FBD = 2.500 lb
FDE = [(2.500 lb * 3 ft) / 5 ft] * 2
→
FDE = 3.000 lb
Análisis nodo B
1.000 lb
B
4
3
3
FBD = 2.500 lb
FBC
4
FBE
+ ↑ ΣFy = 0
-1.000 lb - (4/5) * 2.500 lb – (4/5) FBE = 0
FBE = 5 [ -1.000 L - (4/5) * 2.500 lb] / 4
FBE = 3.750 lb
→
FBE = - 3.750 lb
↑
+ → ΣFX = 0
FBC – 1.500 lb – 2.500 Lb * 3/5 – 3.750 * 3/5 = 0
FBC = 1.500 lb + 2.500 Lb * 3/5 + 3.750 * 3/5
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
→
FBC = 5250 lb
Pagina 17 de 26
ESTATICA
Análisis nodo E
FBE = 3.750 lb
FEC
5
4
5
3
FED = 3.000 lb
4
3
E
RE = 10.000 lb
+ → ΣFx = 0
3.000 lb + 3.750 lb * 3/5 + FEC * 3/5 = 0
(-3.000 lb - 3.750 lb * 3/5) 5
FEC =
→
FEC = -8.750 lb
←
FEC = 8.750 lb
3
Análisis nodo C
Cy = 7.000 lb
FCE = 8.750 lb
C
4
3
Cx = 0
FCE = 8.750 lb
ΣFx = - 5.250 lb + 8.750 lb * 3/5 = - 5.250 lb + 5.250 lb = 0
ΣFy = - 7.000 lb + 8.750 lb * 3/5 = - 7.000 lb + 7.000 lb = 0
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Con los valores de FCE y
FCB se pueden determinar
las reacciones Cx y Cy
considerando el equilibrio
de este nodo.
Pagina 18 de 26
ESTATICA
EJERCICIO 6.4 (PROPUESTO)
Con el método de los nodos, determine la fuerza en cada elemento de la
armadura mostrada en la figura. Para cada elemento establezca se este se
encuentra en tensión o en compresión.
1.8 kN
A
2,4 KN
2m
C
B
1.5m
D
2,1 m
CUERPO LIBRE
1.8 kN
A
2,4 KN
2m
C
B
FBx
D
RC
FBy
1.5m
2,1 m
+ ∑ MB = 0
-2,4 k N * 3,6 m + RC * 1.5 m + 1,8 kN * 2 m = 0
RC = (2,4 k N * 3,6 m - 1,8 kN * 2 m) / 1.5 m
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
→
RC = 3,36K N
Pagina 19 de 26
ESTATICA
+↑ ∑ Fy = 0
Fby + RC - 2,4 k N = 0 →
Fby = - RC + 2,4 k N
Fby = - 3.36 kN + 2.4 kN →
Fby = - 0.96 kN
Fby = 0.96 kN
↓
+ → ∑ Fx = 0
Fbx - 1,8 k N = 0 →
Fbx = 1,8 k N
Análisis del Nodo D.
2.4 kN
FDA
FDA
2.4 kN
DA
2m
D
FDC
.2.1 m
FDC
Calculo de CA.
DA2 = (2 m)2 + (2.1 m)2 →
DA = 2.9 m
Aplicando la Ley del Seno
2.4 kN
FDA
=
2m
FDC
=
2.9 m
2.1 m
FDA = 2.4 kN * 2.9 m / 2 m
→
FDA = 3.48 kN
FDC = 2.4 kN * 2.1 m / 2 m
→
FDC = 2.52 kN
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 20 de 26
ESTATICA
Análisis del Nodo B.
FBA
2.5
FBx
B
2
1.5
FBC
RC
+↑ ∑ Fy = 0
Fby - FAB * (2/2.5) m = 0
→
FAB = (0.96 kN * 2.5 m )/ 2 m
FAB = 1.2 kN
+ → ∑ Fx = 0
Fbx + FBC + FAB * (1.5/2.5) m = 0
FBC = - Fbx – FAB * (1.5/2.5) m
FBC = - 1.8 kN – 1.2 kN * (1.5/2.5) m
→
FBC = - 2.52 kN
FBC = 2.52 kN ←
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 21 de 26
ESTATICA
Análisis del Nodo C.
FCA
FCB
B
FCD
RC
+↑ ∑ Fy = 0
RC + FAC = 0
→
FAC = - RC
→
FAC = - 3.36 kN
FAC = 3.36 kN ↓
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 22 de 26
ESTATICA
EJERCICIO 6.5 (PROPUESTO)
Con el método de los nodos, determine la fuerza en cada elemento de la
armadura mostrada en la figura. Para cada elemento establezca se este se
encuentra en tensión o en compresión.
6 KN
A
3 KN
3 KN
1,5 m
C
B
D
E
1m
Cuerpo Libre
2m
2m
1m
6 kN
A
3 kN
3 kN
1.5 m
C
B
Fcx
1m
D
Fcy
2m
RD
2m
E
1m
+ ∑ MC = 0
3 k N * 1 m – 6 kN * 2 m + RD * 4 m - 3 kN * 5 m = 0
RD = (6 k N * 2 m + 3 kN * 5 m - 3 kN * 1 m) / 4 m
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
→
RD = 6 k N
Pagina 23 de 26
ESTATICA
+↑ ∑ Fy = 0
FCy + RD - 3 k N – 6 Kn – 3 kN = 0 →
→
FCy = 3 k N + 6 Kn + 3 kN - 6 k N
FCy = 6 k N
+ → ∑ Fx = 0
Calculo de medidas.
AE2 = (1.5 m)2 + (3 m)2
→
AE = 3.35 m
→
AD = 2.5 m
AE = AB = 3.35 M
AD2 = (1.5 m)2 + (2 m)2
AD = AC = 2.5 M
Análisis del Nodo E.
3 kN
FEA
FEA
3 kN
3.35 m
1.5 m
E
FED
FED
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
3m
Pagina 24 de 26
ESTATICA
Aplicando la Ley del Seno
3 kN
FEA
FED
=
=
1.5 m
3.35 m
3m
FEA = 3 kN * 3.35 m / 1.5 m
→
FEA = 6.7 kN
FED = 3 kN * 3 m / 1.5 m
→
FED = 6.0 kN
Análisis del Nodo D.
FDA
1.5
FDC
2.5
2
D
FDE
RD
+↑ ∑ Fy = 0
RD + FDA * (1.5 / 2.5) m = 0
→
FDA = (- RD * 2.5 m) / 1.5 m
FDA = (- 6kN * 2.5 m) / 1.5 m
→
FDA = - 10 k N
→
FDC = - 2 kN
FDA = 10 k N ↓
+ → ∑ Fx = 0
- FDC + FDA * (2 / 2.5) m + FDE = 0
FDC = - 10 kN * (2 / 2.5) m + 6 kN
FDC = 2 kN ←
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 25 de 26
ESTATICA
Nota:
Como la estructura es simétrica entonces tenemos que:
FEA =FBA=6.7 kN
FDA = FCA = - 10 k N
FEC = FCB = 6 kN
Elaborado por: Cesar Alcalá/Wilmer Camacho
Sección II-332
Pagina 26 de 26