DISTRIBUCIONES DE PROBABILIDAD DE VARIABLE ALEATORIA

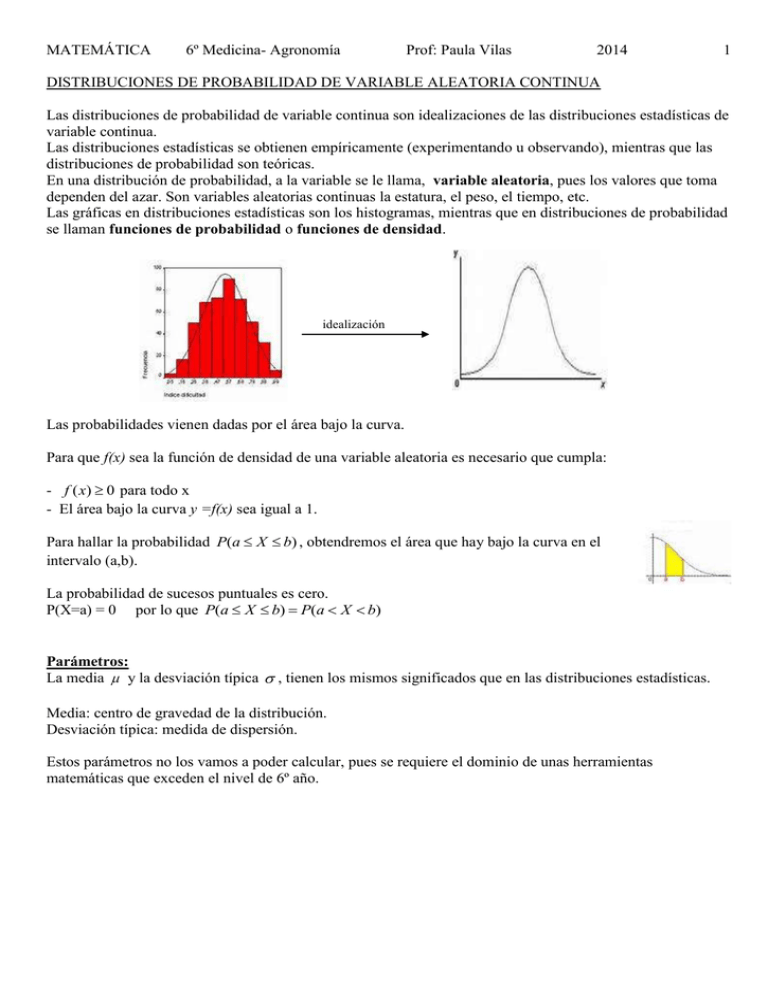
MATEMÁTICA
6º Medicina- Agronomía
Prof: Paula Vilas
2014
1
DISTRIBUCIONES DE PROBABILIDAD DE VARIABLE ALEATORIA CONTINUA
Las distribuciones de probabilidad de variable continua son idealizaciones de las distribuciones estadísticas de
variable continua.
Las distribuciones estadísticas se obtienen empíricamente (experimentando u observando), mientras que las
distribuciones de probabilidad son teóricas.
En una distribución de probabilidad, a la variable se le llama, variable aleatoria, pues los valores que toma
dependen del azar. Son variables aleatorias continuas la estatura, el peso, el tiempo, etc.
Las gráficas en distribuciones estadísticas son los histogramas, mientras que en distribuciones de probabilidad
se llaman funciones de probabilidad o funciones de densidad.
idealización
Las probabilidades vienen dadas por el área bajo la curva.
Para que f(x) sea la función de densidad de una variable aleatoria es necesario que cumpla:
- f ( x)  0 para todo x
- El área bajo la curva y =f(x) sea igual a 1.
Para hallar la probabilidad P(a  X  b) , obtendremos el área que hay bajo la curva en el
intervalo (a,b).
La probabilidad de sucesos puntuales es cero.
P(X=a) = 0 por lo que P(a  X  b)  P(a  X  b)
Parámetros:
La media  y la desviación típica  , tienen los mismos significados que en las distribuciones estadísticas.
Media: centro de gravedad de la distribución.
Desviación típica: medida de dispersión.
Estos parámetros no los vamos a poder calcular, pues se requiere el dominio de unas herramientas
matemáticas que exceden el nivel de 6º año.
MATEMÁTICA
6º Medicina- Agronomía
Prof: Paula Vilas
2014
LA DISTRIBUCIÓN NORMAL
La Campana de Gauss o Curva Normal, es una función de probabilidad continua, simétrica, cuyo máximo
coincide con la media  .
Esta curva fue descrita por el matemático alemán
Carl Friedrich Gauss.


La gran importancia de esta distribución se debe a la enorme frecuencia con que aparece en las situaciones
más variadas. Entre las muchas variables que se distribuyen normalmente, se puede citar:
- Caracteres morfológicos de individuos (personas, animales, plantas) de una misma raza. Por ejemplo:
tallas, pesos, etc.
- Caracteres fisiológicos. Por ejemplo: efectos de una misma dosis de un fármaco o de una misma
cantidad de abono.
Para cada valor de  (media) y cada valor de  (desviación típica), hay una curva normal que se denomina
N ( , ) .
Por ejemplo:
N(0,4)
N(10,5)
N(20,5)
Cálculo de probabilidades en una distribución normal
Ejemplo: el cociente intelectual de un grupo de personas se distribuye mediante una normal N(110,10).
Sabiendo que P(100<X<120) = 0,6826, calcula:
P(X<110) =
P(X<100) =
2
MATEMÁTICA
6º Medicina- Agronomía
P(X>120) =
Prof: Paula Vilas
P(X<120) =
Curva Normal N(0,1)
En la distribución N(0,1) a la variable se la suele representar con la letra Z.
Para calcular probabilidades en esta distribución N(0,1) se dispone de una tabla
que nos da las probabilidades P(Z<k) para valores de k de 0 a 3,5, de centésima
en centésima.
El valor de k se busca asi:
- Unidades y décimas en la columna de la izquierda.
- Centésimas en la fila de arriba.
El número que nos da en la tabla es el valor de P(Z<k).
Ejemplos: P(Z<0,45) = 0,6736
P(Z<1,2) = 0,8849
Cálculo de probabilidades en una distribución N(0,1)
P(Z<1,73) =
P(Z>1,73) =
P(0,21<Z<1,34) =
2014
3
MATEMÁTICA
6º Medicina- Agronomía
Prof: Paula Vilas
2014
4
P(Z<-0,83) =
P(-0,83<Z<2,3) =
P(-1,95<Z<-1) =
En general:
-
k0
La probabilidad P (Z<k) se encuentra directamente en la tabla.
0 k
La probabilidad P (Z>k) = 1 – P(Z<k)
-
0 k
La probabilidad P (Z< -k) = P(Z>k) = 1 – P(Z<k)
-
-k 0
Cálculo de probabilidades en una distribución N (  ,  )
Las probabilidades en dos distribuciones normales cualesquiera se reparten de forma análoga. Por tanto, para
calcular probabilidades en una distribución N (  ,  ) , se relaciona con la N(0,1), para la cual se dispone del
recurso de la tabla.
N ( , )
N(0,1)
Áreas iguales
0
  0,5 
  1, 4
-0,5
0
1,4
P(  0,5  X   ,14 )  P(0,5  Z  1, 4)
En general: si X es una variable aleatoria con distribución N (  ,  ) , para calcular la probabilidad P(h<X<k)
se realiza:
k  
h
P(h  X  k )  P 
Z 
 
 
Este cambio de variable se denomina tipificación de la variable.
La variable ya tipificada sigue una distribución N(0,1).
MATEMÁTICA
6º Medicina- Agronomía
Prof: Paula Vilas
2014
Tabla de distribución normal N(0,1)
Los valores de la tabla normal representan el área bajo la curva normal hasta un valor positivo de k.
5
MATEMÁTICA
6º Medicina- Agronomía
Prof: Paula Vilas
2014
PRÁCTICO 7
1) En la distribución N(0,1), calcula las siguientes probabilidades:
a) P(Z>1,3)
d) P(1,3<Z<1,96)
b) P(Z<-1,3)
e) P(-1,3<Z<1,96)
c) P(Z>-1,3)
f) P(-1,96<Z<-1,3)
2) En la distribución normal N(173,6), halla las siguientes probabilidades:
a) P(X<173)
d) P(161<X<180,5)
b) P(X>180,5)
e) P(X>191)
c) P(174<X<180,5)
f) P(X=174)
3) Las estaturas de los individuos de una población se distribuyen normalmente con media 175cm y
desviación típica 10cm. Calcula la probabilidad de:
a) un individuo tenga una estatura mayor que 180cm.
b) un individuo tenga una estatura menor de 170cm.
c) ¿Qué proporción de individuos tiene una estatura comprendida entre 170cm y 180cm?
4) La talla media de los 200 alumnos de un centro escolar es de 165cm y la desviación típica 10cm. Si las
tallas se distribuyen normalmente, calcula la probabilidad de que un alumno elegido al azar mida más de
180cm. ¿Cuántos alumnos puede esperarse que midan más de 180cm?
5) Los pesos de 2000 soldados presentan una distribución normal de media 65kg y desviación típica 8kg.
Calcula la probabilidad de que un soldado elegido al azar pese:
a) más de 61 kg.
b) entre 63kg y 69kg.
c) menos de 71kg.
d) más de 75kg.
6) El tiempo necesario para que una ambulancia llegue a un centro deportivo se distribuye según una
distribución normal de media 17minutos y desviación típica 3min. Calcula la probabilidad de que el tiempo
de llegada esté comprendido entre 13 min y 21 min.
7) La duración de un tipo de pilas eléctricas sigue una distribución normal con media 50horas y desviación
típica 5hrs. Halla la probabilidad de que, eligiendo una pila al azar, dure entre 40hrs y 55hrs.
6