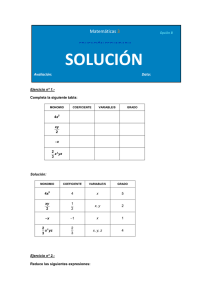
SERIE INTRODUCTORIA. REPASO DE ALGEBRA . 2

SERIE INTRODUCTORIA. REPASO DE ALGEBRA .
1.- REDUCCION DE TÉRMINOS SEMEJANTES.
Recuerde que los términos semejantes son aquellos que tienen las mismas letras con los
mismos exponentes. Ejemplos:
*7m;
*8x2; x2
5m
*6ab2; 2b2a
Sólo se pueden reducir aquellos términos que son semejantes y se efectúa sumando o restando
los coeficientes numéricos y manteniendo la misma parte literal.
a) 3x2y– (x2y - 2xy2) + 3x2y
Sol. 5x2y + 2xy2
b) 3x + 2y – (x – (x - y)
Sol. 3x + 3y
c) – [-(a – 2b) – (a + 2b) – (-a - 3b)]
Sol. a – 3b
d) 3x + 2y – {2x – [3x – (2y - 3x) -2x] -y}
Sol. 5x + y
e) 2 f) – {5a –b – [3b- (c – b + 2a) -4a] + c}
Sol. 2 Sol. -11a + 5b – 2c
g) 3xy – { -(2xy + 4x) + [3y- (-xy + x+ 2xy)]}
Sol. 6xy+5x-3y
h) – {a - 2ab + b –[3a + 5ab + 6b –(a - b) + 5]}
Sol. a + 7ab - 6b + 5
2.- MULTIPLICACION DE EXPRESIONES ALGEBRÁICAS
Tips.
Recuerde la regla de los signos de la multiplicación y las leyes de los exponentes.
Para multiplicar un polinomio por un monomio, se multiplica el monomio por cada término
del polinomio.
Para multiplicar un polinomio por otro polinomio, cada término de un polinomio se multiplica
por todos y cada uno de los términos del otro polinomio y se reducen términos semejantes.
a) (-4abc) (-3a2b2) (2ab5c7) Sol. 24a4b8c8
b) (2xy2) (4x2y)
Sol. 8x3y3
c) (-4/5x2y3z4) (3/8x2y3)
d) (x2yz)(-5x3y2)(-2y3z2)
e) (m2 + n2- mn) (2m - 3n)
f) (3x-1)3
Sol. 3/10 x4y6z4
Sol. -5x5y3z -2x2y4z3
Sol. 2m3 – 5m2n + 5mn2- 3n3
Sol. 27x3 – 27x2 +9x – 1
h) –(x + y) -2(-3x-3y) + y(x-3) - (-3y) + x(y-1)
i) {-(a + b) - [2a(3a - 2b)] - (a2 - a) + b} – a(a+b)
g) (x2 +2x -2)2
Sol. x4 + 4x3- 8x + 4
Sol. 4x + 5y + 2xy
Sol. -8a2 + 3ab
Juan Inclán Rico
2
3.- PRODUCTOS NOTABLES
Dentro de la multiplicación algebraica existen algunos productos que pueden ser desarrollados
directamente sin necesidad de efectuar toda la operación.
a) Cuadrado de un binomio
2
2
(a + b) = a + 2ab + b
2
2
2
(a - b) = a - 2ab + b
2
b) Diferencia de Cuadrados
(a + b) (a – b) = a – b
2
2
2
2
3
Suma de Cubos
(a + b)(a – ab + b ) = a + b
Diferencia de Cubos
(a - b )( a + ab + b ) = a - b
2
2
3
3
3
c) Cubo de un binomio
3
3
2
2
(a + b) = a + 3a b + 3ab + b
3
3
3
2
2
(a - b) = a - 3a b + 3ab - b
3
d) Producto de binomios con término común
2
(x + a) (x + b) = x + x(a+b) + ab
a) (a – 5) (a + 11)
Sol. No se proporciona.
f) (b2 + 1/4) (b2 – ½)
b) (7x - 2/3)(7x + 2/3)
g) (2b2 + 3c4)2
c) (2x2 – 1)3
h) (5y – π)2
d) i) (am – bn)3
j) (√3a2 + √2b2) (√3a2 - √2b2)
e) (√2 + y) (√2 – y)
4.- DIVISION DE EXPRESIONES ALGEBRAICAS
Tips.
Se utilizan las reglas de la división de signos y algunas leyes de los exponentes.
Al dividir un polinomio entre un monomio se divide cada término del polinomio entre el
monomio, uno a la vez.
Para dividir dos polinomios; ambos se colocan en orden decreciente (de mayor a menor
exponente) con respecto a una variable; si falta algún término en los polinomios se
sustituyen por cero
Se aplica un algoritmo similar al utilizado en la división de números naturales.
a)
! "# $ %&
b) ! " $ Sol.
Sol.
" $ Juan Inclán Rico
c)
d)
e)
' Sol. # # ' ( (
! " ! " ' ! "
Sol.
! "
f) (x2 + 7x + 10) / (x + 2)
g) (8x3 – y3) / (2x – y)
3
Sol. 8xy + 12 x3y5w4 - 9x2w3
"
!"
+ 2a2b4
Sol. x + 5
Sol. 4x2 + 2xy + y2
h) (3x4 +4x3 – 32x2 - 5x – 20) / (3x3 - 8x2 – 5)
Sol. x + 4
i) (-5a4b - 7a3b2 – 4a2b3 – 7ab4 – 5b5) / (a2 + 2ab +b2)
Sol. -5a2b + 3ab2 -5b3
5.- DIVISION SINTETICA
Es una forma abreviada de efectuar la división entre dos polinomios, la condición es que el
divisor debe de ser un binomio de la forma x - a donde a es un número positivo o negativo.
Para efectuar este tipo de divisiones se debe considerar lo siguiente:
Ambos polinomios (dividendo y divisor) deben estar ordenados en forma decreciente (de
mayor a menor exponente) con respecto a una variable y si falta un término en los
polinomios éste se sustituye por cero.
Se extraen los coeficientes numéricos de cada término de los polinomios.
Para comenzar a dividir se baja el primer número, se multiplica por el divisor y se suma
con el siguiente número y asi sucesivamente como se ilustra en el ejemplo:
(2x3 – 9x2 +7x + 6) / (x – 3)
dividendo
-9
7
6
divisor
6
-9 -6
3| 2
-3
-2
0
Cociente
Resolver por división sintética.
Sol. 2x2 -3x -2
2
residuo
)
'
a) (2x3 +5x2 +10x -8) / (x+3)
sol. 2x2 –x +13 -
b) (x3 – 125) / (x – 5)
sol. x2 +5x +25
c) (2y3 +8y2 -17y +10) / (y + 6)
sol. 2y2 -4y +7 - '
d) (x5 +5x4 +3x3 +2x2 +8x +8) / (x + 3)
sol. x4 +2x3 -3x2 +11x -25 + '
e) (3y2 – 12) / (y - 2)
sol. 3y + 6
6.- LEYES DE LOS EXPONENTES
Recuerde las leyes de los exponentes
Ley
1
x =x
Ejemplo
61 = 6
Juan Inclán Rico
x0 = 1,,
70 = 1
x
4-1 = 1/4
x-1 = 1/x
x2x3 = x2+3 = x5
xmxn = xm+n
x4/x2 = x4-2 = x2
xm/xn = xm-n
(xm)n = xmn
(x2)3 = x2×3 = x6
(xy)n = xnyn
(xy)3 = x3y3
(x/y)n = xn/yn
(x/y)2 = x2 / y2
x-n = 1/xn
x-3 = 1/x3
Realice las operaciones y exprese el resultado en exponentes positivos.
a) x7 / x3 = _____________
____
f) (2x/3)-2 = _____________
-3 2 4
b) x x x = ____________
___
g) (x2/y)-3 = _____________
-2 3
c) (x-3)-2 = ______________
____
h) (-2xy
(
) = _____________
d) (3x4)-2 = _____________
__
i) (
e) 3(x4)-2 = _____________
_
j) (-3x-2y3z-4)-2= ___________
k)
l)
m)
n)
ñ)
Sol.
o)
p) y3b + 2 ( y2b + 4)2
Sol. y7b + 10
q)
7.- LEYES DE LOS RADICALES
significa
=ay
) = _______________
y se lee como “raíz
raíz cuadrada positiva de a” ······
Definiciòn de Raìz N−èsima:
Si n es cualquier entero positivo, entonces la raíz n-èsima
n èsima principal de a se define como
y si n es par, se tiene que
PROPIEDADES DE LAS RAICES NESIMAS:
1.
2.
3.
4.
si n es impar
5.
si n es par
4
Juan Inclán Rico
Definición de los exponentes racionales
Para cualquier exponente racional
expresado en su forma más simplificada, donde m y n
son enteros y
, se define
O equivalentemente,
Y si n es par, se requiere que
De acuerdo a esta definición, las leyes de los exponentes también son válidas para
p
los
exponentes racionales
Simplificar los siguientes radicales
radicales:
_________________
¿
6)
____________________
2)
__________________
7)
_____________________
3)
__________________
8)
______________________
4)
_________________
9)
____________________
10)
____________________
5)
Reducir radicales semejantes.
5
Juan Inclán Rico
6
Juan Inclán Rico
Factorización de trinomios de la forma ax2 +bx + c = 0
Factorize las expresiones siguientes:
7
Juan Inclán Rico
Completar un Trinomio Cuadrado Perfecto.
En muchas ocasiones es necesario este procedimiento. El método a seguir depende del
término que falte. Practiqué completando los siguientes trinomios.
a) 9x2 + ___ + 16b4
d) ____ + 20b6c3 + 4c6
b) x6 – 6b2x3 + ____
e) 4a2 + 4a + ____
3 3
6
c) ___ + 2x y + x
f) x6 + _____ + 4y4
IÓN DE ECUACIONES DE PRIMER GRADO CON UNA INCÓGNITA.
9.- RESOLUCIÓN
Para resolver una ecuación de primer grado con una incógnita basta con despejar el término
independiente. Practique con las siguientes ecuaciones. Recuerde las técnicas repasadas
anteriormente.
8
Juan Inclán Rico
10.- RESOLUCION DE SISTEMAS DE DOS ECUACIONES CON DOS INCÓGNITAS.
9
Juan Inclán Rico
10
10.- RESOLUCION DE ECUACIONES DE SEGUNDO GRADO
Ecuaciones
ciones de segundo grado incompletas.
*De la forma ax2 + bx = 0
Una de sus raíces siempre es cero.
Para resolverla se factoriza, utilizando a x como factor común x(ax +b) = 0. Se iguala
cada factor a cero y se despeja la x.
* De la forma ax2 + c = 0
Sus soluciones son el mismo número pero de signo contrario (uno positivo y uno
negativo)
Para resolverla se despeja a la x utilizando el doble signo de la raíz.
Ecuaciones de segundo grado completas.
Ax2 + bx + c= 0 Estas se pueden resolver de tres maneras:
Factorización
Completando el trinomio cuadrado perfecto
Fórmula general
Por factorización. Se factoriza la ecuación, cada factor se iguala a cero y se despeja la x.
Practiqué con los siguientes ejercicios.
Juan Inclán Rico
Por el método de completar cuadrados: Se suma o resta el término faltante para completar
un trinomio cuadrado perfecto sin
s alterar la ecuación original.
Por fórmula general.
Donde a: Coeficiente del término cuadrático
b: Coeficiente del término lineal
c: Término independiente
La expresión dentro del radical se conoce como el discrimante b2 – 4ac y nos da información
sobre la naturaleza de las soluciones o raíces de la ecuación.
Si b2 – 4ac > 0 la ec. de segundo grado tiene dos soluciones reales
Si b2 – 4ac = 0 la ec. de segundo grado tiene una solución real y una imagi
imaginaria
Si b2 – 4ac < 0 la ec. de segundo grado tiene dos soluciones imaginarias.
11