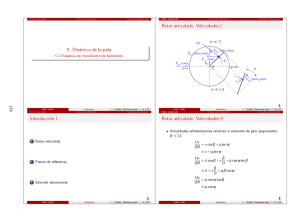
5.2 Dinámica del movimiento de batimiento. Efecto de la posición de

Velocidades I
dFb
5. Dinámica de la pala
5.2 Dinámica del movimiento de batimiento. Efecto de la posición de la
articulación de batimiento
P
z
¯
e bR
B
dFc
dFI
z
Plano de referencia
r
El movimiento de la pala consiste en una rotación alrededor de la
articulación de batimiento caracterizada por el ángulo β .
147
AAD (HE)
Dinámica
eb ∕= 0.
Dinámica pala
1 / 11
AAD (HE)
eb ∕= 0.
Dinámica pala
3 / 11
Velocidades II
Introducción
En general, la articulación de batimiento suele separarse del eje de
rotación. Esto se traduce en general en las siguientes consecuencias:
representa un diseño mecánico más simple,
Se añade un modo ηb (x ) para caracterizar el movimiento fuera del
plano, z , de forma que z = ηb (x )β (t )R .
La ventaja de añadir este modo es que la formulación puede ser
fácilmente adaptada a modos de exión más complejos.
Para el caso particular que se va a considerar de rotación de sólido
rígido el modo ηb (x ) se expresa como
⎧
⎨ (x − eb )
ηb (x ) =
1 − eb
⎩
la frecuencia natural de la dinámica de batimiento aumenta con
respecto a
Dinámica
Ω
proporcionando mejores características de manejo del
rotor,
0
existe un momento de batimiento que es transmitido al eje de rotación.
x > eb
x < eb
donde la forma del modo se ha normalizado para que ηb (1) = 1.
La velocidad en la dirección perpendicular a la pala, UP , se expresa
adimensionalmente (considerando ángulos pequeños)
Los valores habituales de posición de la articulación de batimiento
suelen ser del orden de 3 % al 5 % del radio del rotor.
UP
ż
dz
β̇
≈λ+
+ µ cos ψ
≈ λ + ηb + µ cos ψηb′ β
ΩR
ΩR
dr
Ω
AAD (HE)
Dinámica
eb ∕= 0.
Dinámica pala
2 / 11
AAD (HE)
Dinámica
eb ∕= 0.
Dinámica pala
4 / 11
Equilibrio de momentos I
Equilibrio de momentos III
donde:
dFb fuerza aerodinámica: dFb ≈ dL
dFc fuerza centrífuga dFc = m r Ω2 dr
dFI fuerza de inercia: dFI = m z̈dr = m (ηb R )β̈ dr
M̄b =
d F̄b =
Se desprecian los efectos de la gravedad y de la velocidad radial.
Equilibrio de momentos con respecto la articulación de batimiento,
∑ MB = 0
∫ R
eb R
∫ R
148
eb ∕= 0.
Dinámica
Dinámica pala
5 / 11
Equilibrio de momentos II
∫ R
1 − eb eb R
(ηb R )r m dr =
∫ R
eb R
(ηb R )2 m dr +
Reb R
(η R )m dr
1 − eb eb R b
∫
se obtiene:
+
(∫ R
2
)
(ηb R ) m dr β̈ +
eb R
)
∫ R
∫
Reb R
2
(ηb R ) m dr +
(ηb R )m dr Ω2 β =
(ηb R )dFb
1 − eb eb R
eb R
eb R
(∫ R
resultando nalmente:
AAD (HE)
ηb d F̄b
dFb
ρ (ΩR )2 cR
∫R
eb R eb R (ηb R )m dr
νb = 1 +
∫
1 − eb eR R (ηb R )2 m dr
2
b
νb2 = 1 +
∫1
eb eb ηb m dx
∫
1 − eb e1 ηb2 m dx
b
AAD (HE)
eb ∕= 0.
Dinámica
Dinámica pala
7 / 11
Equilibrio de momentos IV
Debido a la expresión de ηb , se cumple que:
1
eb
y νb es la frecuencia propia adimensional de batimiento:
∫ R
(ηb R )(r − eb R )m β̈ dr +
(ηb R )r m Ω2 β dr −
(r − eb R )dFb = 0
eb R
eb R
(∫ R
)
(∫ R
)
2
(1 − eb )
(ηb R ) m dr β̈ +
(ηb R )r m dr Ω2 β =
eb R
eb R
∫ R
=R
(x − eb )dFb
eb R
AAD (HE)
∫ 1
β ′′ + νb2 β = γ M̄b
Dinámica
El primer término, 1, representa la frecuencia propia debida a la rigidez
centrífuga mientras que el segundo es el efecto de la posición de la
articulación de batimiento. Por tanto separar la articulación de
batimiento consigue aumentar la frecuencia propia del sistema
dinámico con respecto la frecuencia propia de un rotor articulado.
En general la frecuencia propia se suele expresar también como:
νb2 = 1 +
donde mb es la masa de la pala, rc la posición radial ∫del centro de
masas de la pala con respecto a la articulación, Ib = eRb R (ηb R )2 m dr
es el momento de inercia con respecto a la articulación.
Caso particular de masa uniforme:
νb2 = 1 +
eb ∕= 0.
Dinámica pala
6 / 11
mb rc
Ib
AAD (HE)
Dinámica
3 eb
2 1 − eb
eb ∕= 0.
Dinámica pala
8 / 11
Equilibrio de momentos V
Solución estacionaria I
Dado que el valor de la posición de la articulación de batimiento puede
ser entre 4 % a 5 %, la frecuencia propia del rotor es ligeramente
superior a la velocidad de rotación (νb ∼ 1,02 − 1,04). Por tanto, el
desfase entre la acción exterior y la respuesta del sistema es
ligeramente inferior a 90º.
Momento aerodinámico
M̄b =
∫ 1
ηb (
e
2
)
(
)
θ (x + µ sin ψ)2 − λ + ηb β ′ + ηb′ µβ cos ψ (x + µ sin ψ) dx
Desarrollando estos términos:
M̄b = Mθc θc + Mθ1 θ1 + Mλ λ + Mβ β + Mβ ′ β ′
149
AAD (HE)
eb ∕= 0.
Dinámica
Dinámica pala
9 / 11
Equilibrio de momentos VI
Desarrollando los términos se obtiene:
1
1
1
8
3
4
Mθc = c2 + c1 µ sin ψ + c0 µ 2 sin2 ψ
Mθ1 =
1
10
1
1
4
6
c3 + c2 µ sin ψ + c1 µ 2 sin2 ψ
1
1
6
4
Mλ = − c1 − c0 µ sin ψ
1
1
Mβ = − f1 µ cos ψ − f0 µ 2 cos ψ sin ψ
6
4
1
1
8
6
Mβ ′ = − d1 − d0 µ sin ψ
donde los siguientes coecientes modican la solución
c0 = 1 − eb ; c1 = 1 − (eb + eb2 )/2; c2 = 1 − (eb + eb2 + eb3 )/3
c3 = 1 − (eb + eb2 + eb3 + eb4 )/4, d0 = 1 − eb ; d1 = 1 − (2e + eb2 )/3
f0 = 1; f1 = eb /2
AAD (HE)
Dinámica
eb ∕= 0.
Dinámica pala
10 / 11
La solución estacionaria es de la forma
f1 (β0 , β1c , θ0 ) = 0
f2 (β0 , β1s , β1c , θ1c ) = 0
f3 (β1s , β1c , θ0 , θ1s ) = 0
Las expresiones detalladas se pueden encontrar en Johnson pg. 232
La mayor diferencia que aparece respecto del caso articulado consiste
en el acoplamiento entre el control lateral y longitudinal.
AAD (HE)
Dinámica
eb ∕= 0.
Dinámica pala
11 / 11