cuerpos redondos. la esfera terrestre

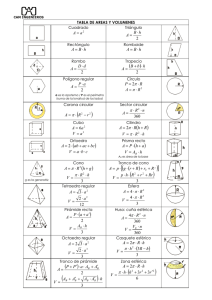
IES PEÑAS NEGRAS. Geometría. 3º ESO.
Departamento de Matemáticas
CUERPOS REDONDOS. LA ESFERA TERRESTRE
1. CUERPOS REDONDOS.
Un cuerpo redondo es un sólido que contiene superficies curvas. Dentro de los cuerpos
redondos los más interesantes son los cuerpos de revolución.
Los cuerpos de revolución son los cuerpos geométricos que se forman al girar una figura plana
alrededor de un eje.
Actividad 1. ¿Cuáles de las siguientes figuras son cuerpos redondos? ¿Cuáles son cuerpos de revolución?
¿De cuáles conoces el nombre? Razona tus respuestas.
A
B
C
D
E
F
G
H
I
J
2. CILINDRO
El cilindro es un cuerpo redondo limitado por una superficie cilíndrica y dos bases paralelas. La
superficie cilíndrica es una superficie curva formada por infinitos segmentos paralelos. Los
cilindros pueden ser:
- Rectos, si los segmentos que forman la superficie cilíndrica son perpendiculares a las bases.
- Oblicuos, si los segmentos que forman la superficie cilíndrica no son perpendiculares a las
bases.
El cilindro de revolución recto es un cuerpo de revolución
generado por el giro de un rectángulo o cuadrado alrededor de uno
de sus lados. Coloquialmente lo llamaremos cilindro.
Los elementos del cilindro son:
- Las bases, dos círculos iguales y paralelos.
- La superficie lateral o superficie cilíndrica que es la cara lateral
no plana que une las bases.
- El radio del cilindro que es el radio de las bases.
- El eje es el lado del paralelogramo que, al girar sobre si
mismo, genera la superficie cilíndrica.
- La generatriz, es el lado opuesto al eje que genera la
superficie cilíndrica.
- La altura, es la distancia entre las bases.
Actividad 2: Indica los elementos del cilindro en la siguiente figura.
IES PEÑAS NEGRAS. Geometría. 3º ESO.
Departamento de Matemáticas
Desarrollo de un cilindro:
Al desarrollar un cilindro recto obtenemos un rectángulo (o cuadrado) y
dos círculos iguales que son sus bases. La base del rectángulo es la
longitud de la circunferencia de la base y la altura del rectángulo es la altura
(que coincide con la generatriz) del cilindro. Veáse la figura:
Al desarrollar un cilindro oblicuo obtenemos un romboide (o rombo) y
dos círculos iguales que son sus bases. La base del romboide es la longitud
de la circunferencia de la base y la altura del romboide es la altura (que no
coincide con la generatriz) del cilindro. Veáse la figura:
Área de un cilindro:
o Área lateral, el área del paralelogramo que se obtiene en el
desarrollo.
AL 2
r h
r2
Área de la base, el área del círculo. AB
Área total del cilindro es la suma del área lateral más el área de
las dos bases.
AT AL 2 AB
donde r es el radio de la base y h es la altura del cilindro.
o
o
Volumen de un cilindro: V
AB h
Actividad 3: Responde a las siguientes cuestiones:
a. Calcula el área del cilindro.
b. Calcula su volumen.
Actividad 4: Responde a las siguientes cuestiones, sabiendo que r = 2 dm, d = 2 y
h = 5 dm
a. Calcula el área del cilindro.
b. Calcula su volumen.
d
3. CONO
Cuerpo redondo limitado por una superficie cónica y por una base
plana. La superficie cónica está formada por infinitos segmentos con
un punto común, llamado vértice. Los conos pueden ser:
- Rectos: cuando el vértice equidista de los puntos frontera de su
base, un círculo. El eje de rotación es perpendicular a la base.
- Oblicuos: cuando el vértice no equidista de los puntos frontera
de su base, un círculo. El eje de rotación no es perpendicular a la base.
El cono de revolución recto es un cuerpo de revolución generado
por el giro de un triángulo rectángulo alrededor de uno de sus catetos.
Coloquialmente lo llamaremos cono recto o cono.
Los elementos del cono recto son:
- Las base que es un círculo.
- La superficie lateral o superficie cónica que es la cara lateral no
plana que une la base con el vértice.
IES PEÑAS NEGRAS. Geometría. 3º ESO.
-
-
-
Departamento de Matemáticas
El radio del cono es el radio de la
base.
El eje es el cateto del triángulo
rectángulo que, al girar sobre él,
genera la superficie cónica.
La generatriz, es la hipotenusa del
triángulo rectángulo que genera la
superficie cilíndrica.
La altura, es la distancia entre la
base y el vértice.
Actividad 5: Indica los elementos del
cono en la siguiente figura.
Desarrollo de un cono:
Al desarrollar un cono recto obtenemos un sector circular y un
círculo. La longitud de arco del sector circular es 2
r (con r el
radio del cono) y su radio es la generatriz del cono. Veáse la
figura:
Área de un cono:
o Área lateral, el área del sector circular que se obtiene en el
desarrollo. AL
r g
r2
Área de la base, el área del círculo. AB
Área total del cono es la suma del área lateral más el área de
la base.
AT AL AB
donde r es el radio de la base y g es la generatriz del cono.
o
o
Volumen de un cono:
V
AB h
3
Actividad 6: Responde a las siguientes cuestiones, siendo R = 3 cm y h = 4 cm.
a. Calcula el área del cono.
b. Calcula su volumen.
Actividad 7: Responde a las siguientes cuestiones, siendo R = 6 cm y g = 10 cm
a. Calcula el área del cono,
b. Calcula su volumen.
4. TRONCO DE CONO
Un tronco de cono recto se forma al cortar un cono recto por un plano paralelo a la
base. Los troncos de cono tienen dos bases circulares de diferente tamaño y una cara
lateral curva.
Un tronco de cono recto es un cuerpo de revolución que se genera al rotar un
trapecio rectángulo alrededor de su lado perpendicular.
Los elementos del tronco de cono recto son:
- Las bases que son los círculos (base mayor y base menor)
IES PEÑAS NEGRAS. Geometría. 3º ESO.
-
Departamento de Matemáticas
La superficie lateral es la cara lateral no plana que une las dos bases.
Los radios del tronco de cono son los radios de las bases.
El eje, lado del trapecio rectángulo que, al girar sobre él, genera la superficie cónica.
La generatriz, es el lado del trapecio rectángulo que no es base ni el eje.
La altura, es la distancia entre las bases.
La altura del tronco (h), la diferencia de los radios (R-r) y la generatriz (g) forman un triángulo
rectángulo.
Desarrollo de un tronco de cono recto:
Al desarrollar un tronco de cono recto obtenemos un trapecio circular y
dos círculos. La longitudes de arco del trapecio circular son: 2
R y
2
r (con R es el radio mayor y r es el radio menor) y su diferencia de
radios es la generatriz del tronco de cono. Veáse la figura:
Área de un tronco de cono:
o Área lateral: es el área del sector circular que se obtiene en el desarrollo. AL
o
Área de las bases: AB
(R
2
(R r) g
2
r )
o Área total del cono es la suma del área lateral más el área de la base.
AT AL AB
donde R es el radio mayor, r es el radio menor, g es la generatriz y h es la altura del cono.
Volumen de un tronco de cono:
V
R2
r2
3
Rr h
Actividad 8: Responde a las siguientes cuestiones:
a. Calcula el área del tronco de cono.
b. Calcula su volumen.
5. ESFERA.
Una esfera es un cuerpo redondo limitado por una superficie esférica. La superficie esférica es
una superficie curva cerrada cuyos puntos equidistan de otro interior llamado centro de la esfera.
Una esfera es un cuerpo de revolución que se genera al
rotar un semicírculo alrededor de su diámetro.
Los elementos de la esfera son:
- El centro de la esfera, el punto que equidista de todos
los puntos de la superficie esférica que delimita a la
esfera
- El radio de la esfera, cada uno de los segmentos que
unen un punto de la superficie esférica con el centro.
También se le llama así a la longitud común de estos segmentos.
La esfera es un cuerpo redondo cuya superficie esférica que lo delimita no es desarrollable en
el plano. Es decir, no es posible extender la superficie esférica en un plano de forma exacta. A lo
largo de la historia se han aportado diferentes tipos de representaciones planas de la superficie
esférica, todas ellas muy relacionadas con la representación plana del globo terrestre.
Área de una esfera:
A 4
r2
donde r es el radio de la esfera.
IES PEÑAS NEGRAS. Geometría. 3º ESO.
r3
4
V
Volumen de una esfera:
Departamento de Matemáticas
donde r es el radio de la esfera.
3
Actividad 9: Responde a las siguientes cuestiones:
a. Calcula el área de una esfera de radio r = 3 cm.
b. Calcula el volumen de dicha esfera.
Actividad 10: En tu vida cotidiana observa a tu alrededor y encuentra ejemplos de objetos (aparatos,
utensilios, edificios, formas de la naturaleza, …) con forma de cuerpo redondo. Anota el objeto y el tipo de
cuerpo redondo.
OBJETO
1.
2.
3.
TIPO DE CUERPO REDONDO
6. FIGURAS ESFERICAS.
6.1. Casquete esférico.
Cada una de las partes que se forman en la superficie esférica al
cortarla por un plano.
Área del casquete esférico:
Acasquete
2
r h
h 2 3r h
3
Volumen del casquete esférico: Vcasquete
Actividad 11: Responde a las siguientes cuestiones:
a. Calcula el área del casquete esférico de radio, r = 7 cm, y altura, h = 3 cm.
b. Calcula el volumen de dicho casquete esférico.
6.2. Zona esférica.
Parte de la superficie esférica comprendida entre dos planos paralelos.
La porción de esfera delimitada por dos planos paralelos se denomina
segmento esférico.
Área de la zona esférica:
Azona
2
r h
Volumen de la zona esférica: Vsegmento
h h2
3R 2
6
3r 2
Actividad 12: Responde a las siguientes cuestiones:
a. Calcula el área de la zona esférica de radios, R = 9 cm y r = 7 cm, y altura, h = 3 cm.
b. Calcula el volumen del segmento esférico.
6.2. Huso esférico.
Parte de la superficie esférica comprendida entre dos planos secantes que
pasan por el centro de la esfera. La porción de esfera delimitada por dos planos
secantes que pasan por el centro de la esfera se denomina cuña esférica.
Área del huso esférico:
Ahuso
Área de la cuña esférica: Vcuña
r2
360
4
r3
3 360
4
α
IES PEÑAS NEGRAS. Geometría. 3º ESO.
Departamento de Matemáticas
Actividad 13: Responde a las siguientes cuestiones:
a. Calcula el área del huso esférico de radio, r = 8 cm, y amplitud α = 45º.
b. Calcula el volumen de la cuña esférica.
7. LA ESFERA TERRESTRE.
7.1. Elementos de la esfera terrestre.
- Eje terrestre: Eje imaginario de la Tierra
cuando gira sobre sí misma. Sus extremos
son el Polo Norte y el Polo Sur.
- Ecuador: Es la circunferencia máxima
perpendicular al eje de la Tierra. Divide a la
Tierra en dos Hemisferios, el Hemisferio
Norte y el Hemisferio Sur. Los Polos están
separados 90º del Ecuador.
- Meridianos: Circunferencias que pasan por
los Polos, y que son perpendiculares al
Ecuador. Cada punto de la Tierra tiene su
Meridiano, por lo tanto, hay un número
infinito de ellos. El llamado "Meridiano Cero",
es aquél que sirve de referencia para medir las Longitudes, también se le denomina Meridiano de
Greenwich, ya que pasa por la ciudad inglesa de Greenwich.
- Paralelos: Son las circunferencias paralelas y menores al Ecuador. También hay un número
infinitos de ellos, pero se destacan: el Trópico de Cáncer, el Trópico de Capricornio, el Círculo
Polar Ártico y el Círculo Polar Antártico.
7.2. Coordenadas geográficas.
Los paralelos y meridianos forman una red geográfica de líneas imaginarias que permiten ubicar la
posición de un punto cualquiera en la superficie terrestre. Las Coordenadas Geográficas o
Terrestres son la Latitud y Longitud y se expresan en grados sexagesimales.
-
La Latitud: es la medida en grados, sobre el mismo meridiano, entre el Ecuador y el punto
correspondiente.
 El Ecuador se toma como línea de base, y le corresponde la Latitud de 0º.
 Todos los puntos que estén ubicados en el mismo paralelo, les corresponden la misma
Latitud.
 Puede medir de 0º a 90º, todos aquellos que se encuentren al Sur del Ecuador, reciben
la denominación Sur (S), con signo negativo; y aquellos que se encuentren al Norte del
Ecuador, reciben la denominación Norte (N), con signo positivo.
-
La Longitud: es la medida en grados, sobre el Ecuador, entre el Meridiano Cero y el
meridiano que pasa por el punto correspondiente.
 El llamado Meridiano de Greenwich se toma como línea de base, y le corresponde la
Longitud de 0º.
 Todos los puntos que estén ubicados en el mismo meridiano, les corresponden la
misma Longitud.
IES PEÑAS NEGRAS. Geometría. 3º ESO.


Departamento de Matemáticas
Puede medir de 0º a 180º, todos aquellos que se encuentren al Oriente (Este) del
Meridiano de Greenwich, reciben la denominación Este (E); y aquellos que se
encuentren al Oeste del Meridiano de Greenwich, reciben la denominación Oeste (O).
Los polos Norte y Sur no tienen Longitud.