28 Ejemplos Ejemplo 1. Una manguera de agua de 2.00 cm. de
Anuncio
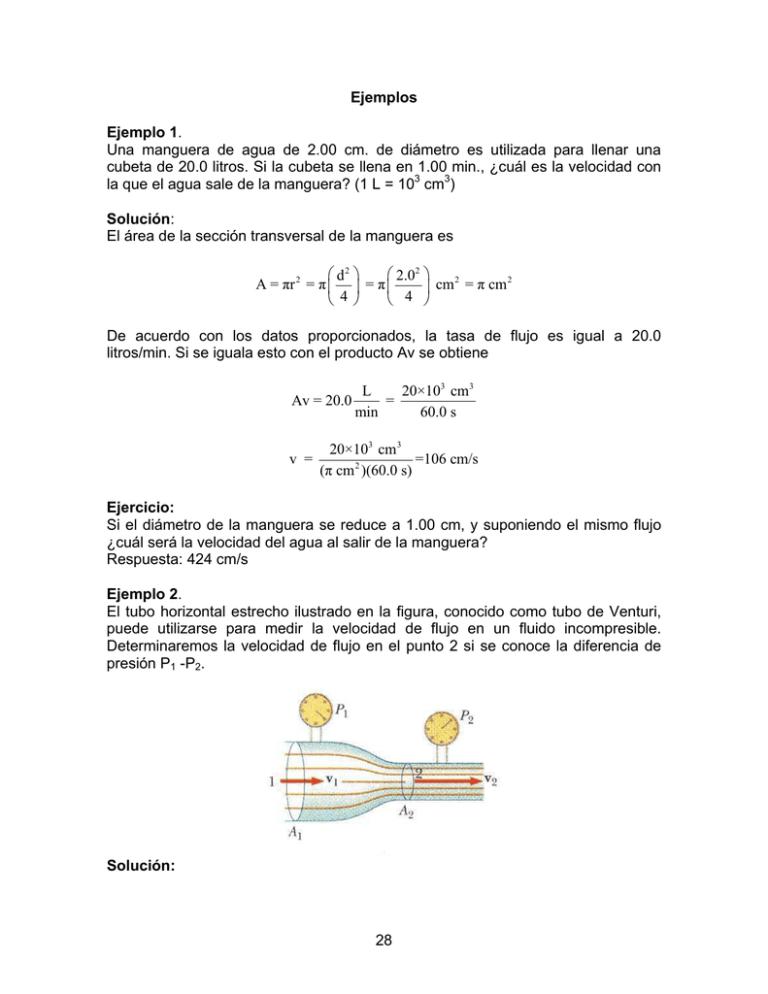
Ejemplos Ejemplo 1. Una manguera de agua de 2.00 cm. de diámetro es utilizada para llenar una cubeta de 20.0 litros. Si la cubeta se llena en 1.00 min., ¿cuál es la velocidad con la que el agua sale de la manguera? (1 L = 103 cm3) Solución: El área de la sección transversal de la manguera es d2 2.02 2 2 A = πr 2 = π = π cm = π cm 4 4 De acuerdo con los datos proporcionados, la tasa de flujo es igual a 20.0 litros/min. Si se iguala esto con el producto Av se obtiene Av = 20.0 v = L 20×103 cm3 = min 60.0 s 20×103 cm3 =106 cm/s (π cm 2 )(60.0 s) Ejercicio: Si el diámetro de la manguera se reduce a 1.00 cm, y suponiendo el mismo flujo ¿cuál será la velocidad del agua al salir de la manguera? Respuesta: 424 cm/s Ejemplo 2. El tubo horizontal estrecho ilustrado en la figura, conocido como tubo de Venturi, puede utilizarse para medir la velocidad de flujo en un fluido incompresible. Determinaremos la velocidad de flujo en el punto 2 si se conoce la diferencia de presión P1 -P2. Solución: 28 Puesto que el tubo es horizontal, y1 = y2, la ecuación de Bernoulli aplicada a los puntos 1 y 2 produce P1 + 1 2 1 ρv1 = P2 + ρv 2 2 2 2 Según la ecuación de continuidad se tiene que A1v1 = A2v2; o bien v1 = A2 v2 . A1 Al sustituir esta expresión en la ecuación anterior se obtiene 2 1 A 1 P1 + ρ 2 v 2 2 = P2 + ρv 2 2 2 A1 2 v 2 = A1 2(P1 - P2 ) ρ(A12 - A 22 ) También se puede obtener una expresión para v1 utilizando este resultado y la ecuación de continuidad. Es decir, 2(P1 - P2 ) v1 = A 2 ρ(A12 - A 22 ) Como A2 < A1, entonces P2 < P1. En otras palabras, la presión se reduce en la parte estrecha del tubo. Este resultado en cierto modo es análogo a la siguiente situación: Considérese un cuarto atestado de personas. Tan pronto se abre la puerta la gente empieza a salir y el arremolinamiento (presión) es menor cerca de la puerta donde el movimiento (flujo) es mayor. Ejemplo 3. Un tanque que contiene un líquido de densidad ρ tiene un agujero en uno de sus lados a una distancia y1 desde el fondo. El diámetro del agujero es pequeño comparado con el diámetro del tanque. El aire sobre el líquido se mantiene a una presión P. Determine la velocidad a la cual el fluido sale por el agujero cuando el nivel del líquido está a una distancia h arriba del agujero. 29 Solución: Debido a que A2 >> A1, el fluido está aproximadamente en reposo en la parte superior, punto 2. Al aplicar la ecuación de Bernoulli a los puntos 1 y 2 y considerando que en el agujero P1 = P0, se obtiene P0 + 1 2 ρv1 + ρgy1 = P + ρgy 2 2 Pero y2 – y1 = h, de manera que v1 = 2(P - P0 ) + 2gh ρ El flujo de agua por el agujero es A1v1. Cuando P es grande comparada con la presión atmosférica P0 (el término 2gh puede ignorarse), la velocidad de salida del flujo es principalmente una función de P. Si el tanque está abierto a la atmósfera, entonces P = Po y v1 = 2gh En otras palabras, la velocidad de salida del flujo para un tanque abierto es igual a la adquirida por un cuerpo que cae libremente desde una altura h. Esto se conoce como la ley de Torricelli. Ejemplo 4. Calcular la potencia de salida de un aerogenerador que tiene un diámetro de aspa de 80 m, suponiendo una velocidad del viento de 10 m/s y una eficiencia total de 15%. Solución: Puesto que el radio del aspa es igual a 40 m, el área de la sección transversal del rotor es A = πr 2 = π(40m) 2 = 5.0 × 103 m 2 30 Si pudiera extraerse 100% de la energía del viento disponible, la máxima potencia disponible sería Potencia máxima = 1 3 ρv = 0.5(1.2 kg/m3) (5.0 X 103 m2) (10 m/s)3 = 3.0 X 106 W 2 Como la eficiencia total es de 15%, la potencia de salida es Potencia = 0.15 (potencia máxima) = 0.45 X 106 W. En comparación, una gran planta de turbina de vapor tiene una salida de potencia de 1 GW. En consecuencia, se requerirían 2200 aerogeneradores para igualar su salida a la potencia de la planta de turbina. El gran número de generadores requeridos para una salida de potencia razonable es, sin duda, una desventaja fundamental de la generación eólica. Ejemplo 5. Medida del coeficiente de viscosidad. Una placa metálica cuya área es igual a 0.15 m2 se conecta a una masa de 8.0 g por medio de una cuerda que pasa sobre una polea ideal (cero masa y sin fricción), como en la figura. Un lubricante que tiene un espesor de película de 0.30 mm es colocado entre la placa y la superficie. Cuando se suelta, la placa se mueve hacia la derecha con una velocidad constante de 0.085 m/s. Encuentre el coeficiente de viscosidad del lubricante. Solución: Debido a que la placa se mueve con velocidad constante, su aceleración es cero. Se mueve hacia la derecha bajo la acción de la fuerza T ejercida por la cuerda y por la fuerza de fricción f asociada al flujo viscoso. En este caso, la tensión es igual en magnitud al peso suspendido; por lo tanto, 31 f = T = mg = (8.0 X 10-3 kg) (9.80m/s2 ) = 7.8 X 10-2N El lubricante en contacto con la superficie horizontal está en reposo, en tanto que la capa en contacto con la placa se mueve a la velocidad de la placa. Suponiendo que el gradiente de velocidad es uniforme, tenemos η= fl (7.8 x 10-2 N) (0.30 x 10-3 m) = Av (0.15 m 2 ) (0.85 m/s) =5.5 x 10-3 Ns/m2 Ejemplo 6. La figura muestra cómo la corriente de agua que sale de un grifo se estrecha conforme va cayendo. La superficie transversal A1 es 1.2 cm2 y la de A2 es 0.35 cm2. Los dos niveles están separados por una distancia vertical h (45 mm). ¿Con qué rapidez fluye el agua del grifo? Solución: Considerando que el flujo de volumen es constante, A1v1 = A2v2. Por otro lado, aplicando la conservación de la energía a un elemento del fluido de masa m, entre 1 1 los 2 puntos, se tiene que K2 + U2 = K1 + U1. Es decir, mv 2 2 + 0 = mv12 + mgh . 2 2 Al eliminar v2 entre las dos ecuaciones y al resolver para v1 se obtiene que 2ghA 22 A12 - A 22 Sustituyendo los valores correspondientes, se obtiene que v1 = 28.6 cm/s. v1 = El flujo = A1v1 = πr12v1 = (3.1416)(1.2 cm2)(28.6 cm/s) = 34 cm3/s. Con este flujo, el chorro tardaría unos 3 s para llenar un recipiente de 100 mI. Ejemplo 7. 32 Un tinaco a una altura h = 32 m y de diámetro D = 3.0 m suministra agua a una casa. Un tubo horizontal en su base tiene un diámetro d = 2.54 cm (1 pulgada). Para atender las necesidades de la casa, el tubo ha de suministrar agua con una rapidez R = 0.0025 m3/s (cerca de 2/3 de galón por segundo). a) Si el agua fluye con la rapidez máxima, ¿qué presión tendría el tubo horizontal? b) Un tubo más pequeño, de diámetro d' = 1.27 cm (0.5 in), abastece el tercer piso de la casa, situado a 7.2 m sobre el nivel del suelo. ¿Cuáles son la rapidez de flujo y la presión del agua en este tubo? No tenga en cuenta la viscosidad del agua. Solución: (a) Aplicamos la ecuación de Bernoulli a lo largo de la línea de corriente ABC que se ve en la figura. En los puntos A y B, se tiene que pA + 1 1 ρv A 2 + ρgh = p B + ρv B 2 + 0 2 2 En A la presión pA = p0, la presión atmosférica. Para la presión en B se obtiene 1 p B = p 0 + ρgh + ρ(v 2A - v B2 ) 2 Por otro lado, considerando que el flujo es constante, se tiene que vAAA = vBAB = Flujo. Considerando el valor del flujo ( = 0.0025 m3/s) y las áreas en cada punto, las velocidades en cada punto son Flujo = 3.5×10-4 m /s AA Flujo vB = = 4.9 m /s AB vA = Nótese que el término 1 2 ρv A en la expresión de pB es muy pequeño comparado 2 1 2 ρv B ;. En otras palabras, la rapidez del flujo en la parte superior 2 del tanque es muy pequeña, debido a su enorme superficie transversal. Ahora se obtiene para la presión en el punto B con el término pB = 1.01 x 105 Pa + (1.0 x l03 kg/m3)(9.8 m/s2)(32 m) 33 - 0.5(1.0 x 103kg/m3)(4.9m/s)2 = 1.01 x 105 Pa + 3.14 x 105 Pa -0.12 x 105 Pa = 4.03 x 105 Pa. Si el agua en el tubo horizontal no fluyera (es decir, si la válvula estuviera cerrada), la presión estática en B incluiría sólo los dos primeros términos, lo cual es igual a 4.15 x 105 Pa. La presión cuando el agua fluye se reduce de este valor estático en la cantidad correspondiente a la presión dinámica. (b) Si se quiere que el tubo más estrecho que conduce al tercer piso tenga la misma rapidez de flujo, la velocidad en C deberá ser Flujo vC = = 19.7 m /s AC es decir, cuatro veces el valor en B. Por otro lado, aplicando la ecuación de Bernoulli entre los puntos A y C se obtiene pA + 1 1 ρv A 2 + ρgy A = pC + ρvC 2 + ρgy C 2 2 o bien pC = p0 + 1 ρ(v 2A - vC2 ) + ρg(y A - y B ) 2 pC = 1.01 x 105 Pa + (0.5)(1.0 x 103 kg/m3)(19.7 m/s)2 +(1.0 x 103kg/m3)(9.8m/s2)(32m - 7.2 m) = 1.01 x 105 Pa -1.95 x 105 Pa + 2.43 x 105 Pa = 1.49 x 105 Pa. Dada la mayor velocidad de flujo a través del tubo más pequeño, la contribución dinámica a la presión es mucho más grande en C que en B. Los efectos estáticos y dinámicos tienden a aminorar la presión en este lugar en relación con B. Ejemplo 8. Un tubo de Pitot se puede emplear para calcular la velocidad del flujo del aire mediante la medición de la diferencia entre la presión total y la presión estática. Si el fluido en el tubo es mercurio, con densidad 13,600 kg/m3, y ∆h = 5 cm, encontrar la velocidad del flujo de aire. Suponga que la densidad del aire es 1.25 kg/m3. 34 Solución: Por conservación de la energía se tiene que 1 ρ aire v 2 = ρ hg g∆h 2 Despejando la velocidad del aire, se obtiene 2ρ hg g∆h v= ρ aire Sustituyendo los valores se obtiene que v = 103.3 m/s. Problemas de opción múltiple Líneas de corriente y la ecuación de continuidad 1. El flujo de un fluido que entra en un lado de un contenedor es 3.0 kg/s; el que sale del otro lado del contenedor es 2.0 kg/s. Suponiendo que el contenedor esté completamente lleno con líquido y que no haya otra forma de que entre o salga, podemos concluir que a) el punto de entrada tiene una sección transversal mayor que el punto de salida. b) la magnitud de la velocidad de entrada es mayor que la de la velocidad de salida. c) debe aumentar la densidad del fluido dentro del contenedor. d) el fluido es incompresible. 2. Un largo tubo recto de sección circular tiene un radio que varía a lo largo del tubo. En él hay un flujo estacionario, sin fuentes ni sumideros. En un punto P1 del tubo el radio es r1 y el flujo es Q1, constante. Más adelante, en el tubo hay un punto P2 donde el radio es r2 = r1/3. (a) El flujo de masa a través de P2 se mide y es igual a Q2 donde Q2/Q1 es A) 9. B) 3. C) 1. D) 1/9. E) dependiente de las densidades del fluido en P1 y P2. (b) La razón de las rapideces de flujo v2/v1 es 35 A) 9, B) 3. C) 1. O) 1/9, E) dependiente de las densidades del fluido en P1 y P2. 3. Una corriente estacionaria de agua cae verticalmente de un tubo. Suponga que el flujo es incompresible, A una distancia d1 debajo del tubo la rapidez del agua es 1,0 m/s y a una distancia d2 la rapidez del agua es 2.0 m/s. ¿Cuál es la razón de la sección transversal del flujo a una altura d1 a la sección transversal de altura d2? A) 4:1 B) 2:1 C) 1:2 O) 1:4 4. Una corriente estacionaria de agua cae verticalmente de un tubo. Suponga que el flujo es incompresible; se parece al de la figura 16-5. ¿De qué manera varía la presión en el agua con la altura en la corriente? A) La presión en el agua es mayor en los puntos más bajos de la corriente. B) La presión en el agua es menor en los puntos más bajos de la corriente. C) La presión en el agua es igual en todos los puntos de la corriente. 5. Un fluido incompresible cruza un tubo horizontal. En un punto del tubo la presión del fluido es p1 y su rapidez es v1. Más abajo la presión es p2 y la rapidez del fluido es 2v1. ¿Qué puede concluirse respecto a p1 y p2 ? A) p1 = p2. B) p1 = 3p2. C) PI -2P2. C) Sólo que PI > P2. 6. Un fluido incompresible atraviesa un tubo horizontal. En un punto del tubo la presión es P1. Más abajo de él la presión es P2 > P1. ¿Qué puede concluirse respecto a las superficies de sección transversal del tubo A1 en el punto 1 y A2 en el punto 2? A) A1 > A2. B) A1 < A2. C) Nada puede concluirse sobre la relación entre Al y A2. Aplicaciones de la ecuación de Bernoulli y la ecuación de continuidad 7. Una bomba es capaz de mantener una diferencia de presión por longitud unitaria en un tubo cilíndrico de radio R1 y produce un flujo de masa Qo. Se quiere reemplazar el tubo por dos tubos cilíndricos más pequeños con radio R2. La bomba mantendrá la diferencia original de presión por longitud unitaria en los dos tubos y la masa total que los atraviesa permanecerá igual a Qo. ¿Cuál es la razón R1/R2? A) 2 B) 2 C) 4 2 D) 4 Problemas 1. Suponga que dos tanques, 1 y 2, con una gran abertura en la parte superior, contienen líquidos diferentes. Debajo de la superficie líquida, en cada tanque se perfora un hoyo pequeño a la misma profundidad, pero el hoyo en el tanque 1 tiene la mitad de la superficie transversal del hoyo en el tanque 2. a) ¿Cuál es la razón ρ1/ρ2 de las densidades de los fluidos, si se observa que el flujo de masa es igual en los dos hoyos? b) ¿Cuál es la razón de las rapideces de flujo (flujo de 36 volumen) en los dos tanques? c) Se quiere igualar las dos rapideces agregando o extrayendo fluido en el tanque 2. ¿Cuál deberá ser la nueva altura del fluido arriba del hoyo en el tanque 2 para que la rapidez de su flujo se iguale a la del tanque 1? 2. Un tanque está lleno de agua hasta una altura H. Se perfora un hoyo en una de sus paredes a una profundidad h debajo de la superficie del agua. (a) Demuestre que la distancia x del pie de la pared donde la corriente choca con el suelo está dada por x = 2 h(H - h) (b) ¿Podría hacerse un hoyo a otra profundidad, de modo que esta segunda corriente tuviera el mismo alcance? De ser así, ¿a qué profundidad? (c) ¿A qué profundidad debería hacerse el hoyo para que la corriente emergente cayera al suelo a la máxima distancia de la base del tanque? ¿Cuál es esa distancia? 3. Un sifón es un aparato para sacar líquido de un contenedor que no se puede ladear. Funciona como se indica en la figura. Debe estar lleno inicialmente, pero una vez que se induce el flujo, el líquido fluirá hasta que su nivel caiga por debajo de la abertura en A. El líquido tiene una densidad ρ y una viscosidad insignificante. (a) ¿Con que rapidez fluye el liquido en C? (b) ¿Qué presión tiene en el punto B? 37 Solución: (a) Supongamos que se coloca un sistema de referencia en el punto A. Aplicando la ecuación de Bernoulli en en punto A y en un punto de la superficie del agua que designamos como D, se tiene: 1 1 ρv A 2 + ρgy A = p D + ρv D 2 + ρgy D 2 2 pA + en el punto D, pD = p0 (presión atmosférica), vD = o, yD = d. En el punto A se tiene pA = ¿?, vA = 0, yA = 0. Con todo lo anterior se obtiene que p A = p 0 + ρgd Ahora se aplica la ecuación de Bernoulli entre el punto A y el punto C: pA + 1 1 ρv A 2 + ρgy A = pC + ρvC 2 + ρgy C 2 2 En el punto C, se tiene que pC = p0, vC = ¿?, yC = -h2. Sustituyendo los valores conocidos en el punto A y los valores conocidos en el punto C, se obtiene: p0 + ρgd = p 0 + 1 ρv C 2 + ρg(-h 2 ) 2 Despejando vC se obtiene la velocidad a la salida del sifón v C = 2g(d + h 2 ) (b). Para calcular la presión en el punto B, se aplica la ecuación de Bernoulli entre el punto C y el punto B: pC + 1 1 ρvC 2 + ρgyC = p B + ρv B 2 + ρgy B 2 2 En en punto C se tiene que v C = 2g(d + h 2 ) , pC = p0, yC = -h2. En el punto B, vB = vC, yB = h1 + d. Sustituyendo en la ecuación de Bernoulli, se obtiene que pB = p0 – ρg(h2 + h1 + d). Obsérvese que la velocidad en B es la misma que la velocidad en C porque el flujo a través de la manguera o sifón es constante. 4. Cuando un objeto está sumergido en un líquido en reposo ¿por qué la fuerza neta sobre el objeto es igual a cero en la dirección horizontal? 38 5. Explique por qué puede flotar una botella sellada llena parcialmente con un líquido. 6. Una placa plana está inmersa en un líquido en reposo. ¿Para qué orientación de la placa la presión sobre su superficie es uniforme? 7. Debido a que la presión atmosférica es aproximadamente 105 N/m2 y el área del tórax de una persona es alrededor de 0.13 m2, la fuerza de la atmósfera sobre el tórax de uno de nosotros es de aproximadamente 13000 N. En vista de esta enorme fuerza, ¿por qué nuestros cuerpos no se colapsan? 8. ¿Cómo determinaría usted la densidad de una roca que tiene una forma irregular? 9. Un pequeño pedazo de acero está pegado a un bloque de madera. Cuando la madera se coloca en una tina con el acero en la parte superior, la mitad del bloque se sumerge! Si el bloque se invierte, de manera que el acero quede bajo el agua, ¿la cantidad sumergida del bloque aumenta o disminuye o permanece igual? ¿Qué pasa con el nivel de agua en el tubo cuando el bloque se invierte? 10. La razón del flujo de agua por un tubo horizontal es 2.00 m3/ min. Determine la velocidad del flujo en un punto donde el diámetro del tubo es a) 10.0 cm. b) 5.0cm. 11. En un gran tanque de almacenamiento lleno se forma un pequeño hoyo en su costado en un punto 16 m abajo del nivel del agua. Si la razón de flujo de la fuga es 2.5 x 10 -3 m3 /min. Determine (a) la velocidad del agua al salir por el hoyo, y (b) el diámetro del hoyo. 12. Un tubo horizontal de 10.0 cm. de diámetro tiene una reducción uniforme que lo conecta con un tubo de 5.0 cm. de diámetro. Si la presión del agua en el tubo grande es 8.0 X 104 Pa y la presión en el tubo más pequeño es 6.0 x 104 Pa, ¿a qué razón circula el agua a través de los tubos? 13. Se bombea agua desde el río Colorado hasta la Villa del Gran Cañón a través de una tubería de 15.0 cm. de diámetro. El río está a 564 m de altura y el pueblo a 2096 m. a) ¿Cuál es la presión mínima con que debe bombearse el agua para llegar a la población? b) Si se bombea 4500 m3 diarios, ¿cuál es la velocidad del agua en la tubería c) ¿Cuál es la presión adicional necesaria para entregar este flujo? (Nota: Usted puede suponer que la intensidad del campo gravitacional y la densidad del aire son constantes en este intervalo de alturas.) 14. Por una manguera contra incendios de 6.35 cm. de diámetro fluye agua a una razón de 0.0120 m3/s. La manguera termina en una boquilla de diámetro interior igual a 2.20 cm. ¿Cuál es la velocidad con la cual el agua sale de la boquilla? 39 15. El túnel de agua Garfield Thomas en la Universidad Estatal de Pensilvania tiene una sección transversal circular que se acorta desde un diámetro de 3.6 m hasta la sección de prueba, cuyo diámetro es de 1.2 m. Si la velocidad de flujo es 3.0 m/s en la tubería de mayor diámetro, determine la velocidad de flujo en la sección de prueba. 16. Un géiser en el parque Yellowstone genera erupciones en intervalos de aproximadamente 1 hora y la altura de la fuente alcanza 40 m. (a) ¿Con qué velocidad sale agua del suelo? (b) ¿Cuál es la presión (arriba de la atmosférica) en la cámara subterránea caliente si su profundidad es de 175 m? 40





