Lógica I - Ejercicios resueltos 5

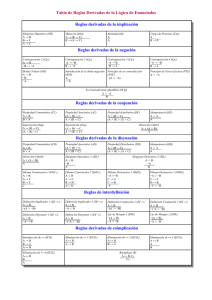
“LÓGICA I”
EJERCICIOS RESUELTOS – 5
(Los ya resueltos en las clases teóricas aparecen recuadrados)
TEMA 5 – DEDUCCIÓN NATURAL. TEOREMAS
Y REGLAS DERIVADAS
EJERCICIO 5.01 ├ A → A
1 (1) A
S
(2) A → A PC 1,1
EJERCICIO 5.02 ├ A → ¬¬A
(ley de doble negación)
1 (1) A
S
1 (2) ¬¬A
DN 1
(3) A → ¬¬A PC 1,2
EJERCICIO 5.03 ├ ¬¬A → A
(ley de doble negación)
1 (1) ¬¬A
S
1 (2) A
DN 1
(3) ¬¬A → A PC 1,2
EJERCICIO 5.04 ├ (A → B) → (¬B → ¬A)
1
2
1,2
1
(1)
(2)
(3)
(4)
(5)
A→B
¬B
¬A
¬B → ¬A
(A → B) → (¬B → ¬A)
EJERCICIO 5.05 ├ ¬(A ∧ ¬A)
(ley de contraposición)
S
S
MT 1,2
PC 2,3
PC 1,4
(principio de no contradicción)
1 (1) A ∧ ¬A
S
(2) ¬(A ∧ ¬A) RA 1,1
1
EJERCICIO 5.06 ├ A ∨ ¬A
1
2
2
1,2
1
1
1
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(principio de tercero excluido)
¬(A ∨ ¬A)
A
A ∨ ¬A
(A ∨ ¬A) ∧ ¬( A ∨ ¬A)
¬A
A ∨ ¬A
(A ∨ ¬A) ∧ ¬( A ∨ ¬A)
¬¬(A ∨ ¬A)
A ∨ ¬A
S
S
I∨ 2
I∧ 1,3
RA 2,4
I∨ 5
I∧ 1,6
RA 1,7
DN 8
EJERCICIO 5.07 ├ A → (A ∧ B) ∨ (A ∧ ¬B)
1
3
1,3
1,3
6
1,6
1,6
1
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
A
B ∨ ¬B
B
A∧B
(A ∧ B) ∨ (A ∧ ¬B)
¬B
A ∧ ¬B
(A ∧ B) ∨ (A ∧ ¬B)
(A ∧ B) ∨ (A ∧ ¬B)
A → (A ∧ B) ∨ (A ∧ ¬B)
EJERCICIO 5.08 A ∨ B, ¬A ├ B
1
2
1
1,2
(1)
(2)
(3)
(4)
A∨B
¬A
¬A → B
B
(1)
(2)
(3)
(4)
A∨B
¬B
¬A → B
A
(silogismo disyuntivo)
S
S
ID∨→ 1
MP 2,3
EJERCICIO 5.09 A ∨ B, ¬B ├ A
1
2
1
1,2
S
PTE
S
I∧ 1,3
I∨ 4
S
I∧ 1,6
I∨ 7
E∨ 2,3,5,6,8
PC 1,9
(silogismo disyuntivo)
S
S
ID∨→ 1
MTP 2,3
2
EJERCICIO 5.10 A ├ B → A
(paradoja del condicional)
1 (1) A
S
1 (2) ¬B ∨ A I∨ 1
1 (3) B → A ID→∨ 2
EJERCICIO 5.11 ¬A ├ A → B
(paradoja del condicional)
1 (1) ¬A
S
1 (2) ¬A ∨ B I∨ 1
1 (3) A → B ID→∨ 2
EJERCICIO 5.12 A ∧ ¬A ├ B
1
2
1,2
1,2
1
1
(1)
(2)
(3)
(4)
(5)
(6)
A ∧ ¬A
¬B
¬B ∧ (A ∧ ¬A)
A ∧ ¬A
¬¬B
B
(ex contradictione quodlibet)
S
S
I∧ 1,2
E∧ 3
RA 2,4
DN 5
EJERCICIO 5.13 ¬(A → B) ┤├ A ∧ ¬B
(a)
1
2
2
1,2
1
1
(b)
1
2
2
1,2
1
(interdefinición de condicional y
conjunción)
¬(A → B) ├ A ∧ ¬B
(1)
(2)
(3)
(4)
(5)
(6)
¬(A → B)
¬(A ∧ ¬B)
A→B
(A → B) ∧ ¬(A → B)
¬¬(A ∧ ¬B)
A ∧ ¬B
S
S
ID→∧ 2
I∧ 1,3
RA 2,4
DN 5
A ∧ ¬B ├ ¬(A → B)
(1)
(2)
(3)
(4)
(5)
A ∧ ¬B
A→B
¬(A ∧ ¬B)
(A ∧ ¬B) ∧ ¬(A ∧ ¬B)
¬(A → B)
S
S
ID→∧ 2
I∧ 1,3
RA 2,4
3
EJERCICIO 5.14 ├ (A → B) ∨ (B → A)
2
2
2
5
5
5
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
A ∨ ¬A
A
B→A
(A → B) ∨ (B → A)
¬A
A→B
(A → B) ∨ (B → A)
(A → B) ∨ (B → A)
(paradoja del condicional)
PTE
S
Pj 2
I∨ 3
S
Pj 5
I∨ 6
E∨ 1,2,4,5,7
EJERCICIO 5.15 ├ (A → B ∧ ¬B) → ¬A
1 (1)
(2)
1 (3)
(4)
A → B ∧ ¬B
¬(B ∧ ¬B)
¬A
(A → B ∧ ¬B) → ¬A
S
PNC
MT 1,2
PC 1,3
EJERCICIO 5.16 ├ A ∨ (A → B)
2
2
4
4
4
(1)
(2)
(3)
(4)
(5)
(6)
(7)
A ∨ ¬A
A
A ∨ (A → B)
¬A
A→B
A ∨ (A → B)
A ∨ (A → B)
PTE
S
I∨ 2
S
Pj 4
I∨ 5
E∨ 1,2,3,4,6
EJERCICIO 5.17 ├ (A → B) ∨ (B → C)
2
2
2
5
5
5
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
B ∨ ¬B
B
A→B
(A → B) ∨ (B → C)
¬B
B→C
(A → B) ∨ (B → C)
(A → B) ∨ (B → C)
PTE
S
Pj 2
I∨ 3
S
Pj 5
I∨ 6
E∨ 1,2,4,5,7
EJERCICIO 5.18 ├ ((A → B) → A) → A
1 (1) (A → B) → A
2 (2) ¬A
S
S
4
2
1,2
1,2
1
1
(3)
(4)
(5)
(6)
(7)
(8)
A→B
A
A ∧ ¬A
¬¬A
A
((A → B) → A) → A
Pj 2
MP 1,3
I∧ 2,4
RA 2,5
DN 6
PC 1,7
EJERCICIO 5.19 (A → B) → B ┤├ A ∨ B
(a)
1
2
2
1,2
1
1
(b)
1
2
3
2,3
5
1,2
1
(A → B) → B ├ A ∨ B
(1)
(2)
(3)
(4)
(5)
(6)
(A → B) → B
¬A
A→B
B
¬A → B
A∨B
S
S
Pj 2
MP 1,3
PC 2,4
ID∨→ 5
A ∨ B ├ (A → B) → B
(1)
(2)
(3)
(4)
(5)
(6)
(7)
A∨B
A→B
A
B
B
B
(A → B) → B
S
S
S
MP 2,3
S
E∨ 1,3,4,5,5
PC 2,6
EJERCICIO 5.20 A → B ∨ C ┤├ (A → B) ∨ (A → C)
(No usar aquí la regla Dt→∨)
(a)
A → B ∨ C ├ (A → B) ∨ (A → C)
1 (1)
2 (2)
2 (3)
2 (4)
2 (5)
1,2 (6)
1,2 (7)
1,2 (8)
1 (9)
1 (10)
(b)
1
2
(distributiva del condicional
en disyunción)
A→B∨C
¬(A → B)
A ∧ ¬B
A
¬B
B∨C
C
A→C
¬(A → B) → (A → C)
(A → B) ∨ (A → C)
S
S
ID→∧ 2
E∧ 3
E∧ 3
MP 1,4
SD 5,6
Pj 7
PC 2,8
ID∨→ 9
(A → B) ∨ (A → C) ├ A → B ∨ C
(1) (A → B) ∨ (A → C) S
(2) A
S
5
3 (3)
2,3 (4)
2,3 (5)
6 (6)
2,6 (7)
2,6 (8)
1,2 (9)
1 (10)
A→B
B
B∨C
A→C
C
B∨C
B∨C
A→B∨C
S
MP 2,3
I∨ 4
S
MP 2,6
I∨ 7
E∨ 1,3,5,6,8
PC 2,9
EJERCICIO 5.21 A → B ├ A ∨ B → B
1 (1) A → B
2 (2) B
(3) B → B
1 (4) A ∨ B → B
S
S
PC 2,2
DilS 1,3
EJERCICIO 5.22 A ∧ B ├ A ↔ B
1
1
1
1
1
1
(1)
(2)
(3)
(4)
(5)
(6)
A∧B
B
A→B
A
B→A
A↔B
S
E∧ 1
Pj 2
E∧ 1
Pj 4
I↔ 3,5
EJERCICIO 5.23 A ∧ ¬B ├ ¬(A ↔ B)
1
2
2
1
1,2
1
(1)
(2)
(3)
(4)
(5)
(6)
A ∧ ¬B
A↔B
A→B
¬(A → B)
(A → B) ∧ ¬(A → B)
¬(A ↔ B)
S
S
E↔ 2
ID→∧ 1
I∧ 3,4
RA 2,5
EJERCICIO 5.24 ¬A ∧ ¬B ├ A ↔ B
1
1
1
1
1
1
(1)
(2)
(3)
(4)
(5)
(6)
¬A ∧ ¬B
¬A
A→B
¬B
B→A
A↔B
S
E∧ 1
Pj 2
E∧ 1
Pj 4
I↔ 3,5
6
EJERCICIO 5.25 A ↔ ¬B, B ∨ C, ¬(A ∧ C), A ├ D
1
2
3
4
3,4
2,3,4
1,4
1,2,3,4
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
A ↔ ¬B
B∨C
¬(A ∧ C)
A
¬C
B
¬B
D
S
S
S
S
SC 3,4
SD 2,5
Sp↔ 1,4
ECQ 6,7
7